考虑不排水强度各向异性的正常固结黏土边坡可靠度研究

曹慧宇?高越?戴可欣?龙安妮

摘要：由于土体沉积过程的影响，土体参数往往具有空间变异性，并且在水平方向和竖直方向上具有不同的空间变异性，表现为各向异性。基于随机有限单元法，考虑土体不排水强度的各向异性，建立正常固结黏土边坡的可靠度分析方法，探究各向异性对边坡可靠度和滑动面的影响规律。通过对参数分析，发现忽略各向异性的影响可能会低估边坡的失效概率，得到不保守结果。同时，不排水强度的变异系数越小，越不能忽略各向异性的影响。根据随机有限单元法程序得到的正常固结黏土边坡滑动面，发现在各向异性的条件下，边坡的滑动面形状呈现部分的线性。

关键词：各向异性;正常固结黏土;随机有限单元法;边坡可靠度

中图分类号：TU 433             文献标识码：A

边坡稳定性问题是岩土工程领域的经典课题之一，边坡的稳定性对基坑开挖、路基建设等工程实践有非常重要的意义。传统方法通常用安全系数来评价边坡的稳定性，而边坡工程具有多种不确定性因素，单一的安全系数并不能对边坡的稳定性进行风险评价。国内外学者考虑边坡稳定的各种不确定性因素，发展和丰富了边坡稳定的可靠度分析方法[1-2]。目前边坡稳定分析的可靠度方法主要有三大类：可靠度估算法[3]、响应面法[4]、蒙特卡罗法[5]。基于蒙特卡罗方法，Griffiths等[6]结合随机场理论[7]和有限元强度折减法[8]，提出了边坡可靠度随机有限元方法。受土体沉积过程的影响，土体参数在水平方向和竖直方向往往具有不同的空间变异性，即各向异性[9]。本文在朱德胜等[10]工作基础上，考虑土体不排水强度参数的各向异性，分析各向异性对正常固结黏土边坡的可靠度以及滑动面的影响规律。

1 各向异性随机场

图1为正常固结黏土边坡的示意图。图中为边坡坡度，H为边坡高度，（=0）为土体内摩擦角，D为约束深度系数，为土体重度。对于正常固结黏土边坡，其坡顶处的不排水强度均值为0，为边坡坡脚处的不排水强度均值。

正常固结黏土边坡的不排水强度均值随深度的变化可表示为：

（1）

式中，为深度为z时的不排水强度均值，为不排水强度均值的增长率。

基于随机场理论，可用相关距离来衡量土体参数的空间变异性。相关距离越小，土体参数的空间变异性越大。在相关距离之内，土体参数之间的相关性较强;而在相关距离之外，土体参数之间则相关性较弱。此外，可用相关函数来表示土体空间内两点的相关系数与距离的关系。

本文采用指数相关函数来模拟不排水强度的各向异性[11]：

（2）

式中，为随机场空间两点之间的相关系数，和分别为随机场空间任意两点在水平方向和竖直方向上的相对距离，和分别为水平和竖直相关距离。

为了保证随机场模拟过程生成土体参数的正值，本文假设正常固结黏土边坡的不排水强度服从对数正态分布。根据统计资料，不排水强度的变异系数通常在0.1至0.5之间[12]，不排水强度的竖直相关距离通常在1m至3m之间[13]。由于土体沉积过程的影响，土体参数在水平方向上的空间变异性往往要小于竖直方向，即水平相关距离往往要大于竖直相关距离。本文采用各向异性系数衡量不排水强度的各向异性程度，该值通常在1到10之间[14]。为了分析各向异性的影响，本文取竖直相关距离m，各向异性系数。

2 正常固结黏土边坡可靠度分析

本文采用随机有限单元法计算正常固结黏土边坡的可靠度。该方法基于蒙特卡罗模拟，在每次模拟中先生成不排水强度的各向异性随机场，然后对边坡施加重力荷載。如果程序在500次迭代以内收敛，则认为边坡稳定;否则，便认为边坡失稳发生破坏。本文中的边坡失效概率为2000次蒙特卡罗模拟中边坡失稳破坏的次数所占的比例。

为与文献[10]中各向同性算例进行对比，图2同样选取边坡坡度、不排水强度的变异系数、边坡安全系数均值分别为1.2、1.4、1.6和1.8时失效概率随各向异性系数的关系曲线。

从图中可以看出：当安全系数均值较小时（），边坡失效概率随各向异性系数呈先增大后减小的趋势，在各向异性系数时失效概率最大，此时正常固结黏土边坡的可靠度最小;当安全系数均值时，边坡失效概率随各向异性系数呈增大的趋势，在时边坡失效概率最大。说明对于正常固结黏土边坡，如果忽略各向异性的影响可能会低估边坡的失效概率，得到不保守的结果。

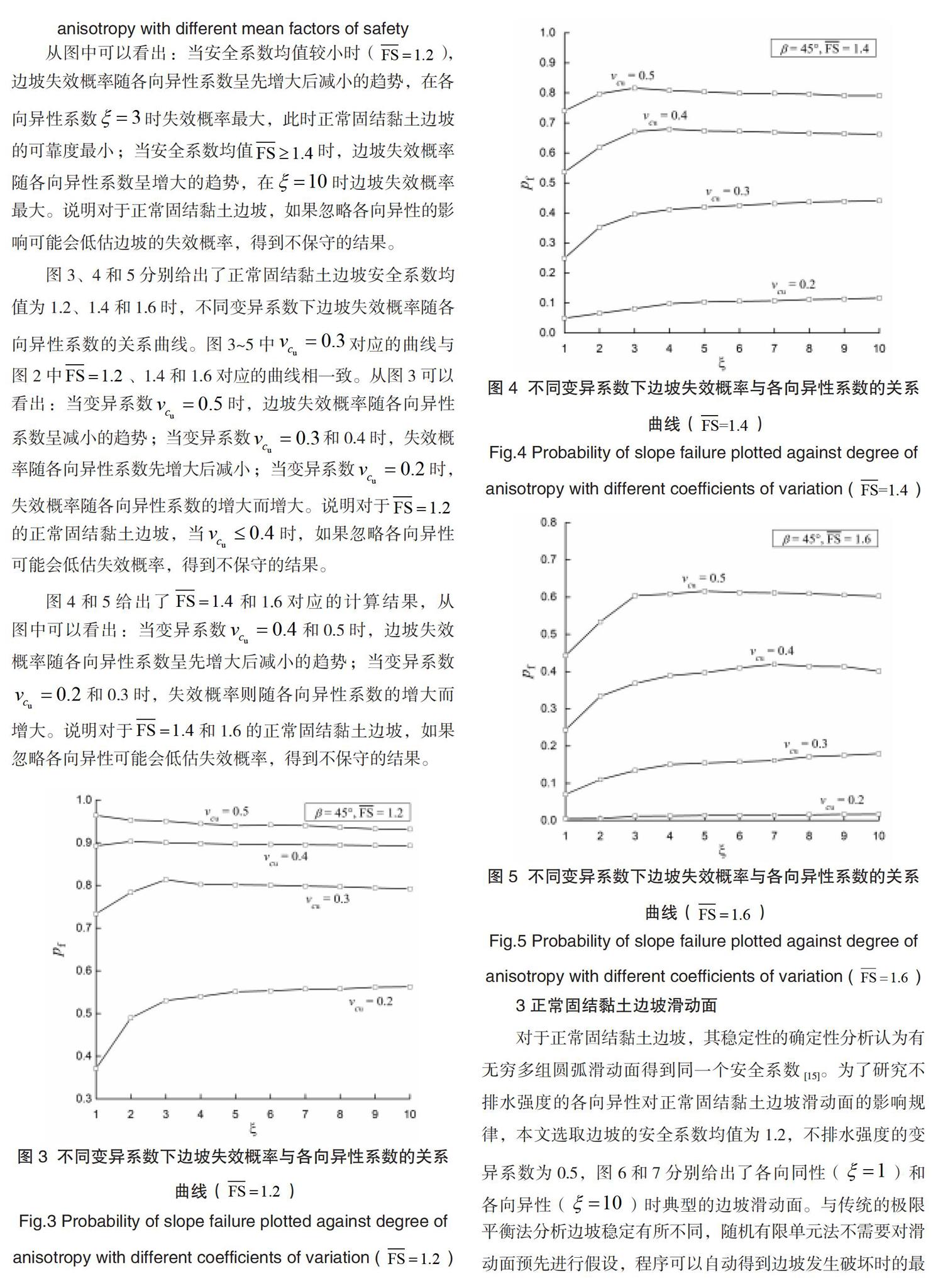
图3、4和5分别给出了正常固结黏土边坡安全系数均值为1.2、1.4和1.6时，不同变异系数下边坡失效概率随各向异性系数的关系曲线。图3～5中对应的曲线与图2中、1.4和1.6对应的曲线相一致。从图3可以看出：当变异系数时，边坡失效概率随各向异性系数呈减小的趋势;当变异系数和0.4时，失效概率随各向异性系数先增大后减小;当变异系数时，失效概率随各向异性系数的增大而增大。说明对于的正常固结黏土边坡，当时，如果忽略各向异性可能会低估失效概率，得到不保守的结果。

图4和5给出了和1.6对应的计算结果，从图中可以看出：当变异系数和0.5时，边坡失效概率随各向异性系数呈先增大后减小的趋势;当变异系数和0.3时，失效概率则随各向异性系数的增大而增大。说明对于和1.6的正常固结黏土边坡，如果忽略各向异性可能会低估失效概率，得到不保守的结果。

3 正常固结黏土边坡滑动面

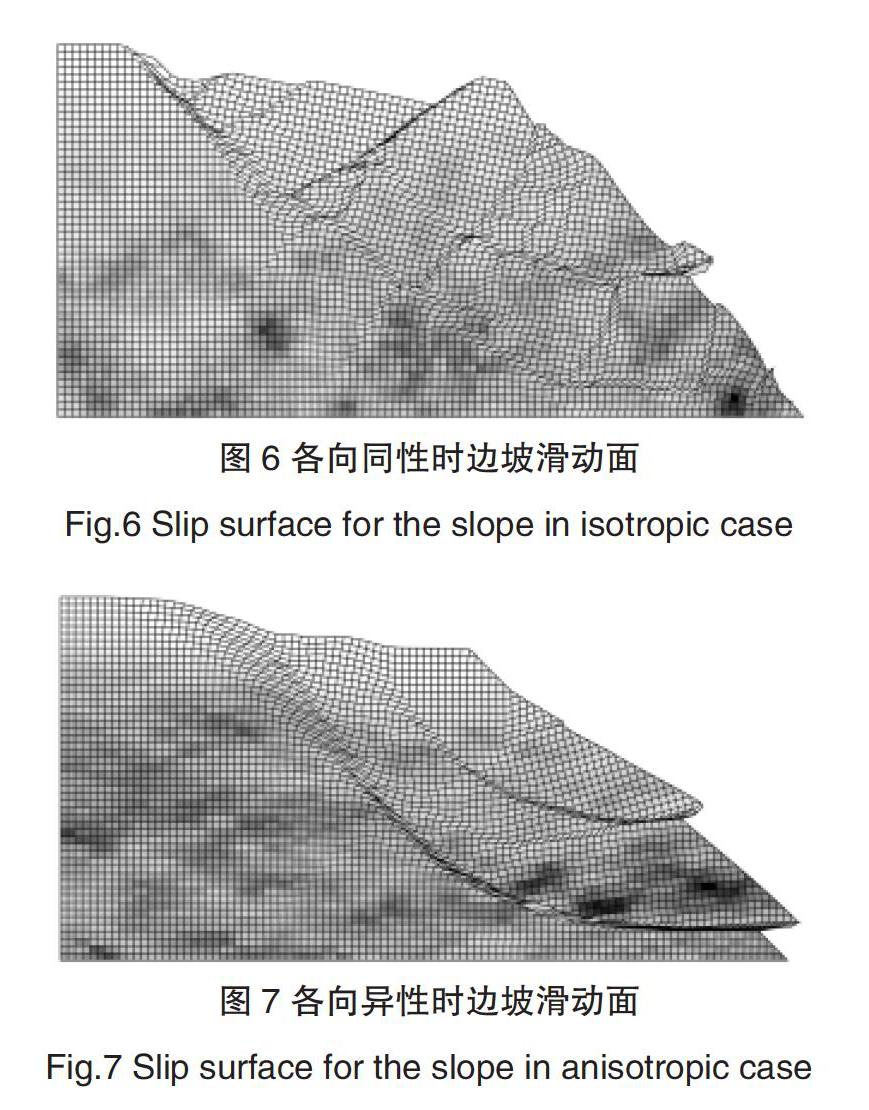
对于正常固结黏土边坡，其稳定性的确定性分析认为有无穷多组圆弧滑动面得到同一个安全系数[15]。为了研究不排水强度的各向异性对正常固结黏土边坡滑动面的影响规律，本文选取边坡的安全系数均值为1.2，不排水强度的变异系数为0.5，图6和7分别给出了各向同性（）和各向异性（）时典型的边坡滑动面。与传统的极限平衡法分析边坡稳定有所不同，随机有限单元法不需要对滑动面预先进行假设，程序可以自动得到边坡发生破坏时的最危险滑动面。图中黑色和白色部分分别代表正常固结黏土边坡不排水强度值高和低的部分。从图6中可以看出：正常固结黏土边坡的滑动面倾向于通过不排水强度值较低的区域，而不是呈现出规则的圆弧形。从图7中可以看出：因选取的水平相关距离是竖向相关距离的10倍，所以不排水强度在竖直方向上的变异性明显要大于水平方向上的变异性。在各向异性条件下，当滑动面通过水平方向上的不排水强度较低区域时，滑动面的形状呈现部分的“线性”。

4 结论

1）本文基于随机有限单元法，考虑土体不排水强度参数的各向异性，对正常固结黏土边坡进行了可靠度计算与分析。

2）对于正常固结黏土边坡，如果忽略各向异性的影响可能会低估边坡的失效概率，得到不保守的结果.不排水强度的变异系数越小，越不能忽略各向异性的影响。

3）在各向异性条件下，正常固结黏土边坡的滑动面形状会呈现部分的“线性”。

参考文献

[1]  DUNCAN J M. Factors of safety and reliability in geotechnical engineering[J]. J Geotech Geoenviron Eng， 2000， 126（4）： 307-316.

[2]  陈祖煜. 建立在相对安全率准则基础上的岩土工程可靠度分析与安全判据[J]. 岩石力学与工程学报， 2018， 37（3）： 521-544.

[3]  JI Jian， ZHANG Chunshun， GAO Yufeng， et al. Effect of 2D spatial variability on slope reliability： A simplified FORM analysis[J]. Geosci Front， 2018， 9（6）： 1631-1638.

[4]  LI Dianqing， ZHENG Dong， CAO Zijun， et al. Response surface methods for slope stability analysis： Review and comparison[J]. Eng Geol， 2016， 203： 3-14.

[5]  ZHU D， GRIFFITHS D V， FENTON G A. Worst-case spatial correlation length in probabilistic slope stability analysis[J]. Géotechnique， 2019， 69（1）： 85-88.

[6]  GRIFFITHS D V， FENTON G A. Probabilistic slope stability analysis by finite elements[J]. J Geotech Geoenviron Eng， 2004， 130： 507-518.

[7]   VANMARCKE E H. Random fields： Analysis and synthesis[M]. Cambridge： MIT Press， 1984.

[8]   GRIFFITHS D V， LANE P A. Slope stability analysis by finite elements[J]. Geotechnique， 1999， 49（3）： 387-403.

[9]   JHA S K. Reliability-based analysis of bearing capacity of strip footings considering anisotropic correlation of spatially varying undrained shear strength[J]. Int J Geomech， 2016， 16（5）： 06016003.

[10]  朱德勝， 高越， 费康. 正常固结黏土边坡可靠度随机有限元分析[J]. 华中科技大学学报（自然科学版）， 2019， 47（7）： 29-33.

[11]  朱德勝，朱佳能，李志刚，等. 基于各向异性随机场的黏土边坡可靠度分析[J]. 扬州大学学报（自然科学版）， 2019， 22（4）： 62-65.

[12]  PHOON K K， KULHAWY F H. Characterization of geotechnical variability[J]. Can Geotech J， 1999， 36（4）： 612-624.

[13]  EI-RAMLY H， MORGENSTERN N R， CRUDEN D M. Probabilistic stability analysis of a tailings dyke on presheared clay–shale[J]. Can Geotech J， 2003， 40： 192-208.

[14]  CHOS E， PARK H C. Effect of spatial variability of cross-correlated soil properties on bearing capacity of strip footing [J]. Int J Numer Anal Meth Geomech， 2010， 34： 1-26.

[15]  GRIFFITHS D V， YU X. Another look at the stability of slopes with linearly increasing undrained strength[J] Géotechnique， 2015， 65（10）： 824-830.