摆线在单叶片真空泵设计中的应用探讨

胡林勇 郑红江 金妙 林希

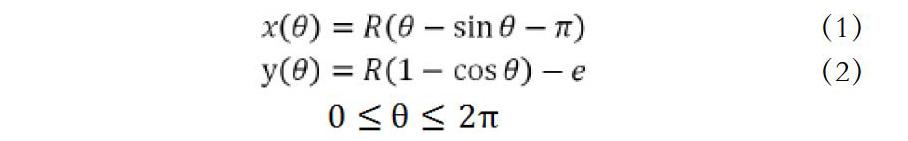
摘 要：汽车刹车助力系统中的真空泵通常采用单叶片设计。在这种设计中，叶片是一块两端为圆弧柱面的矩形平板。工作时，叶片与真空泵转子一起旋转。除了作径向运动，它的两端圆弧柱面必须保持与泵腔内壁曲面相切接触以形成气体密封。这要求泵体内壁曲面的投影为一特殊设计的光滑封闭曲线（泵腔形线）。由于泵腔形线直接决定叶片径向滑动的速度和加速度，因此泵腔形线对真空泵功耗、噪音、和耐久寿命都有较大的影响。本文探讨了摆线在单叶片真空泵设计中的应用，并给出了基于摆线的泵腔形线计算的数学公式。为保证叶片径向滑动加速度是连续的，本文给出了最优叶片长度。

关键词：真空泵;摆线;泵腔型线

1 前言

为了提高汽车发动机的工作效率以达到越来越高的节能减排要求，现代汽车发动机广泛采用涡轮增压技术。这使得刹车助力系统需要独立的真空泵提供助力真空。由于单叶片真空泵结构间单，成本低，被广泛应用到当前的汽车刹车系统中。图1显示单叶片真空泵的基本组成和工作原理。

单叶片真空泵主要由泵体、转子、叶片、泵盖和进排气口单向阀（图中未显示）组成。真空泵转子通常由发动机凸轮轴或曲轴通过连接机构驱动。刹车助力器真空罐被连到图1所示的进气口。当转子被驱动作逆时针方向旋转时，“A”腔容积逐渐变大而从进气口吸入空气，而在“B”腔中的空气被压缩从排气口排出。这样循环往复，连接到进气口的刹车助力器真空罐里的空气被逐渐抽出而形成刹车助力所需的真空。工作时，叶片将随转子旋转并同时作径向滑动。为保持“A”腔和“B”腔的密封，设计时，叶片两端通常选圆柱面，并要求叶片两端圆柱面理论上必须同时保持和泵腔内壁柱面相切。由于叶片被认为是刚体，真空泵泵腔曲面的投影必须是一条特殊设计的封闭曲线。因此，工程计术人员在设计单叶片真空泵时，其主要任务之一就是寻找一条满足上述要求的泵腔形线。在设计时，通常是先确定叶片两端密封柱面中心的轨迹，实际泵体内腔形线则是叶片端面圆的包络线。参考文献[1]探讨了真空泵泵腔形线的数学理论。文献[2]已显示圆弧或椭圆曲线均可用作设计中的参考曲线。本文将研究摆线在真空泵内腔形线设计中的应用，并推导出满足二阶连续泵腔形线公式。对真空泵的设计具有十分重要的参考价值。

2 基于摆线的泵腔形线的产生

在设计单叶片真空泵的泵腔内壁曲线时，通常给定参考曲线。如图2所示，当叶片一个密封端面（柱面）的中心点沿给定的参考曲线从起始点A滑动到参考曲线终点B时，叶片的另一密封端面的中心的轨迹即为泵腔生成曲线。显然点“A”和点“B”是参考曲线和生成曲线的连接点。为了保证真空泵平稳运行，设计时，要求参考曲线和生成曲线在连接点A和B处至少有相同的一阶和二阶导数。亦就是说叶片有连续的滑动速度和加速度。基于这一要求，本文将推道出基于摆线的泵腔生成曲线和泵腔内壁曲线。

从方程（9）可以看出，对于任意给定的叶片矩形部分长度L，转子外半径Rr和叶片密封端面圆弧半径r，参考曲线的偏心距e可以从方程（9）求解， 用（5）可以得到所需摆线生成圆的半径R，从而确定泵腔形线的参考曲线。然而，这样得到的泵腔形线不能保证在生成曲线和参考曲线的连接点“A”和 “B”处叶片的径向滑动加速度是连续的。为了保证叶片滑动加速的连续性，L和e的选取必须受到另外的约束。下面将探讨叶片的径向滑动，从而找出求解L和e的另一约束方程。

3叶片径向滑动速度和加速度

如图2所示，为研究叶片的径向滑动，对参考曲线上任意一点A，分别用和来表示它的极径和极角。应用极坐标和直角坐标的关系，极径和可以被表示为：

4 最优摆线参考曲线的确定

如前所述，为了得到一条保证叶片滑动加数度连续性的参考曲线，叶片长度的选取不能是任意的。因此，下面将探讨约束叶片选取的方程。

在连接点A，极角，参数;在连接点B，极角，，在这两点滑动加数度连续的条件可以被表示为[2]：

把和代入并应用（14）和（15），约束方程（16）可以被简化表示如下：

对于给定的， 联列方程（9）和（17）求解L和e可得到满足叶片滑动加速度连续性的参考曲线，从而得到最优的泵腔形线。由于方程是非线性的，下面将给出简单的尤拉近似求解法。

方程（9）和（17）中消除L得到如下仅含e的方程（假定是提前给定的）：

对于e的第k次近似，一阶尤拉方程根求解法给出其次迭代解为：

给定偏心距e的一个估计 ， 应用（19），（20）和（21）反复迭代，获得工程上足够精确的近似解，叶片矩形部分长度L的最优值可由（17）得到为：

5 计算实例

在这里将显示一个计算实例。微软EXCEL是一个比较好的工具。在這个计算实例中，取转子外半径，叶片密封面圆弧半径为。代入方程（19）-（21）进行反复迭代后得到e的近似值为。代入进入（22），计算得叶片的最优长度。叶片的总长度为78.932 mm。由（5）式求得最优参考摆线生成圆的半径;因此，最佳参考曲线的参数方程由（1）和（2）可得：

将参数作为自变量，用文献[1]给出了计算泵腔封闭曲线的基本公式，可得泵腔形线如图3所示。图中蓝色圆代表转子。图4中，X-轴为转子角位移，蓝色曲线为叶片径向滑动速度系数，红色曲线显示叶片径向滑动的加速度系数。

6 结束语

选择摆线作为单叶片真空泵的泵腔形线设计中的参考曲线时，由于摆线只有一个独立参数偏心距e或摆线生成圆半径R，为了保证叶片径向滑动的加速度是连续的，真空泵叶片的长度不能任意给定而有一个确定的最优值。因此，为了满足真空泵排量要求，泵腔深度将是一个重要参数。

参考文献：

[1]林希.汽车单叶片真空泵设计中的数学理论[J].西安航空学院学报，2013（01）.

[2]林希，李小光.汽车单叶片真空泵设计中的最优椭圆曲线[J].西安航空学院学报，2014（01）.