施工现场设施布局优化问题的新型启发式算法

王家 王洋 邓铁军 刘可心

摘   要：施工现场设施布局的合理性直接关系到项目成本等目标的实现.针对涉及设施较多的施工现场布局优化问题，首先将该离散变量优化问题转换为高维空间的随机抽样问题，进而利用过渡马尔可夫链蒙特卡罗方法的思想，提出一种高效的全局优化启发式算法.与针对连续型高维概率密度分布函数进行随机取样的过渡马尔可夫链蒙特卡罗方法相比，本文提出的启发式算法的框架基础需从概率密度分布函数转变为概率分布函数，进而需在马尔可夫链状态点的产生方法上进行修正，以适应离散型变量优化问题的不同特性.通过实例验证，与目前应用较广的遗传算法相比，本文提出的新型启发式算法在全局最优解的获取稳定性上有较大改进.

关键词：施工现场设施布局优化;启发式算法;全局优化算法;过渡马尔可夫链蒙特卡罗;遗传算法

中图分类号：TU721.2                          文献标志码：A

文章编号：1674—2974（2020）09—0128—09

Abstract：Layout of construction site facilities has great impact on the project objectives， such as project cost. In this paper， the problem of the construction site facilities layout with many facilities， which is an optimization problem with discrete variables， is considered. Firstly， the problem is transformed to a high-dimensional random sampling problem， and then addressed by a novel meta-heuristic algorithm based on transitional Markov chain Monte Carlo （TMCMC）.  Different from original TMCMC developed for optimization problems with continuous variables， the proposed meta-heuristic algorithm is based on introducing a sequence of probability distribution functions instead of probability density functions， and thus the method for iteratively generating states of Markov chains is modified in the proposed algorithm， in order to meet the specifics of optimization problems with discrete variables. As shown in an illustrative example， compared with the widely used genetic algorithm， the proposed meta-heuristic algorithm can obtain higher improvement in the stability of achieving global optimal solution.

Key words：construction site facilities layout optimization;meta-heuristic algorithm;global optimization algorithm;transitional Markov Chain Monte Carlo;genetic algorithm

施工现场设施布局是施工组织设计的重要任务，其目的是在满足场地约束条件下，为一组特定的临时设施分配适当的位置[1]. 施工现场设施布局的科学性和合理性直接关系到施工现场的生产效率和成本节约，进而影响项目成本等目标的实现[2]. 在传统的工程实践中，施工现场设施布局决策主要依靠施工人员的经验，决策的效率较低、不确定性较高[3]. 为提高施工现场设施布局的效率和科学性，国内外的相关学者从不同角度入手，进行了大量的研究工作.

施工现场设施布局问题为组合优化问题，一般利用二次分配问题（Quadratic Assignment Problem，QAP）的模型进行分析，其复杂程度随布局设施的数量增加而急速上升[4].当问题涉及的设施个数较多时，难以采用枚举法或解析方法获得最优解，一般采用元启发式算法（如遗传算法、蚁群算法、粒子群算法等）来得到问题的最优解或近似最优解[5]. 針对施工现场设施布局问题，遗传算法是应用较广的一种元启发式算法.Li和Love针对施工现场设施布局优化问题提出了一种以修饰的边缘重组算子作为交叉算子、以对称基因交换算子作为变异算子的遗传算法[6].Adrian等人比较了遗传算法、粒子群优化算法和蚁群优化算法在不同施工现场设施布局优化问题实例中的性能和效率，结果显示三种算法在解决施工现场设施布局优化问题时的性能和效率相当[7]. 元启发式算法具有随机性，其每次运行获得的最优解不一定相同（不稳定），但现有元启发式算法在全局最优解获取的稳定性上仍有较大的改进空间.

本文基于过渡马尔可夫链蒙特卡罗方法，提出一种针对施工现场设施布局优化问题的新型启发式全局优化算法. 具体而言，针对涉及设施较多的施工现场设施布局优化问题，本文首先将优化问题转换为高维空间的随机抽样问题，进而利用过渡马尔可夫链蒙特卡罗方法的思想，提出一种高效的全局优化启发式算法. 通过实例验证，与应用较广的遗传算法相比，本文提出的优化算法在全局最优解获取的稳定性上有较好的改进.

1   施工现场设施布局优化问题模型

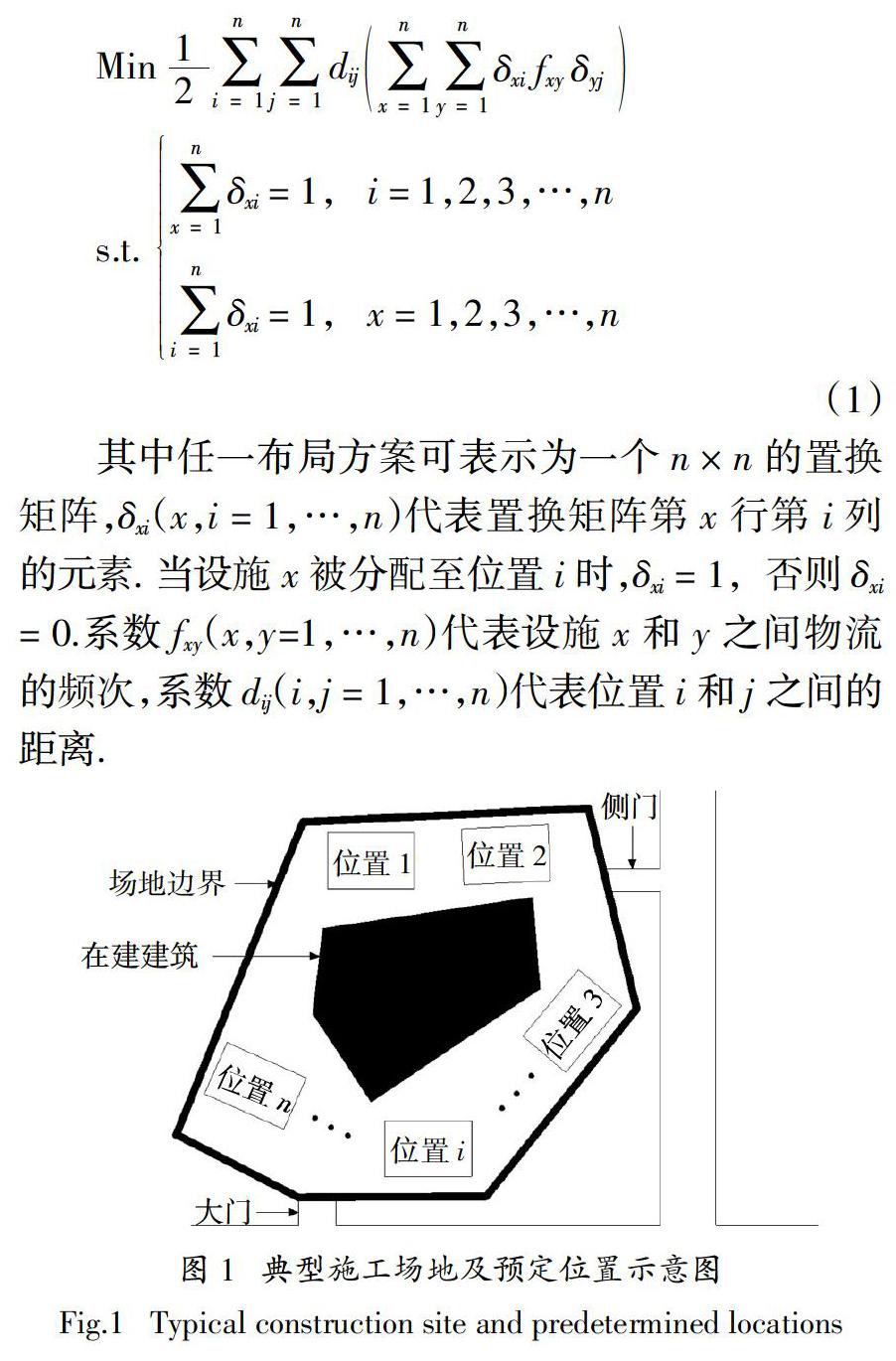
施工现场设施布局优化的目的，在于为一组临时设施分配施工现场的合适位置，以提高施工现场的工作效率，节约成本. 如图1所示，考虑n个临时设施和n个预先确定的施工现场位置，并假定任一预先确定的施工现场位置均足以容纳任一临时设施.以降低临时设施间物流的总移动距离为目的，施工现场设施布局优化问题模型可描述如下：

表1为针对5个临时设施、5个位置的一个布局方案的置换矩阵表示. 置换矩阵的每一行和每一列中均只有一个元素为1，其他元素均为0，该特性可保证公式（1）中的约束条件自动满足. 从物理意义上看，公式（1）中约束条件的含义为：一个位置只能布置一个临时设施，而一个临时设施也只能被分配到一个位置.

上述模型亦适用于将m个临时设施分配至n个位置（n > m）的布局优化问题. 此时，可添加（n - m）个虚拟设施，并将与虚拟设施相关的物流频次fxy赋值为0. 在这种处理方法下，虚拟设施的引入不会影响最终布局优化的结果.

2   施工现场设施布局优化问题的新型启发式算法

针对公式（1）描述的施工现场设施布局优化问题，首先将布局方案的置换矩阵表示转变为向量表示，进而通过建立适当的概率分布函数，将施工现场设施布局优化这一组合优化问题转化为根据给定的高度集中、高维概率分布进行随机抽样的问题，最后给出利用过渡马尔可夫链蒙特卡罗（Transitional Markov Chain Monte Carlo，TMCMC）方法完成随机取样、获取优化问题最优解的方法.本文考虑的施工现场设施布局优化问题为离散型变量优化问题，故其求解过程需解决的是离散型随机概率分布的抽样问题，与原始的TMCMC方法针对的随机抽样问题（针对连续型高维概率密度分布）不同.

因此，在利用TMCMC方法建立施工现场设施布局优化问题的新型启发式算法过程中，需对随机抽样对象以及由此引起的马尔可夫链的构造方法进行修改，以适应施工现场设施布局优化问题的不同特性.

2.1   布局方案的向量表示

描述施工现场设施布局优化模型的公式（1）中，布局方案表示为n × n的置换矩阵.为便于应用本文所提出的启发式方法，布局方案采用含有n个元素的行向量θ = [θ1，θ2，…，θn]来表示，其中行向量的第i个元素代表第i个设施被分配的位置标号. 布局方案的向量表示与置换矩阵表示存在一一对应关系.例如，表1的布局方案可表示为[3，5，2，1，4]，即将临时设施1，2，3，4，5分别分配至位置3，5，2，1，4处.

为满足公式（1）中的约束条件，布局方案行向量中的所有元素需从n个位置标号中选取，且不允许重复，因此可行布局方案的个数为n！. 对应于任一可行布局方案行向量θ = [θ1，θ2，…，θn]，為计算其在公式（1）中的目标函数值g（θ），可先将布局方案行向量转化为对应的置换矩阵，进而利用公式（1）中的目标函数表达式进行计算.

2.2   组合优化问题与随机抽样问题的联系

本文考虑的施工现场设施布局优化这一组合优化问题，与给定概率分布的随机抽样问题存在密切的联系. 在布局方案的向量表示下，可在可行布局方案集合上定义如下概率分布：

式中：g0为预先选定的无量纲化常数，g（θ）为给定可行布局方案θ下的目标函数值，T为温度参数.

在公式（2）定义的概率分布下，具有较小目标函数值（θ）的布局方案θ对应于较大的概率分布. 当温度参数T趋近0时，上述的概率分布（趋近）完全集中在拥有最小目标函数值的可行布局方案（集）上.如对此时的概率分布（对应T趋于0）进行随机抽样，进而在随机抽样的布局方案中选取最优，则可得到施工现场设施布局优化问题的最优解.但是针对高度集中的概率分布，一般的马尔可夫链蒙特卡罗（Markov Chain Monte Carlo，MCMC）方法的抽样效率较差，需经过大量过渡阶段的样本才能得到服从目标概率分布的马尔可夫链样本[8].

2.3   过渡马尔可夫链蒙特卡罗方法

过渡马尔可夫链蒙特卡罗（Transitional Markov Chain Monte Carlo，TMCMC）方法是由Ching和Chen提出的、适用于高度集中的高维概率密度分布函数的高效抽样方法[9]. 该方法在借鉴模拟退火算法[10]思想的基础上，引入了自适应温度下降策略和重抽样方法，以提高算法的抽样性能.针对公式（2）的离散型概率分布的随机抽样问题，利用TMCMC方法，可通过改变温度参数T，引入一组过渡阶段的概率分布（定义在可行布局方案集合上）：

2.4   基于TMCMC的新型启发式优化算法

针对研究的施工现场设施布局优化问题，基于TMCMC，提出的启发式优化算法的流程如下：

3）重复步骤2，直到满足迭代终止原则.本文的迭代终止原则取为达到预先设定的迭代次数.

3   案例分析

为检验基于TMCMC的建议优化算法的性能，并与施工现场设施布局优化领域中采用较广的遗传算法进行对比分析，本文采用两个工程实例进行验证.验证模拟实验使用的计算机硬件配置为处理器 Intel（R）Core（TM）i7-7700、内存16G，软件配置为MATLAB R2017b.

3.1   工程实例一（11项临时设施）

本实例采用文献[6]中的施工现场设施布局优化问题，该问题涉及11个临时设施和11个用以分配临时设施的位置，并假定每个预定位置都足以容纳任一临时设施. 表2提供了11个临时设施的具体信息和编号. 设施中的侧门（设施8）和正门（设施11）通常在开始施工之前就已经确定，在设施分配过程中正门和侧门的位置不会发生变化.但是其它设施与正门及侧门的相对位置仍会影响布局的物流移动总距离（模型的目标函数），因此侧门和正门不能从模型的考察设施中排除，仍需作为模型中的一种特殊约束存在.

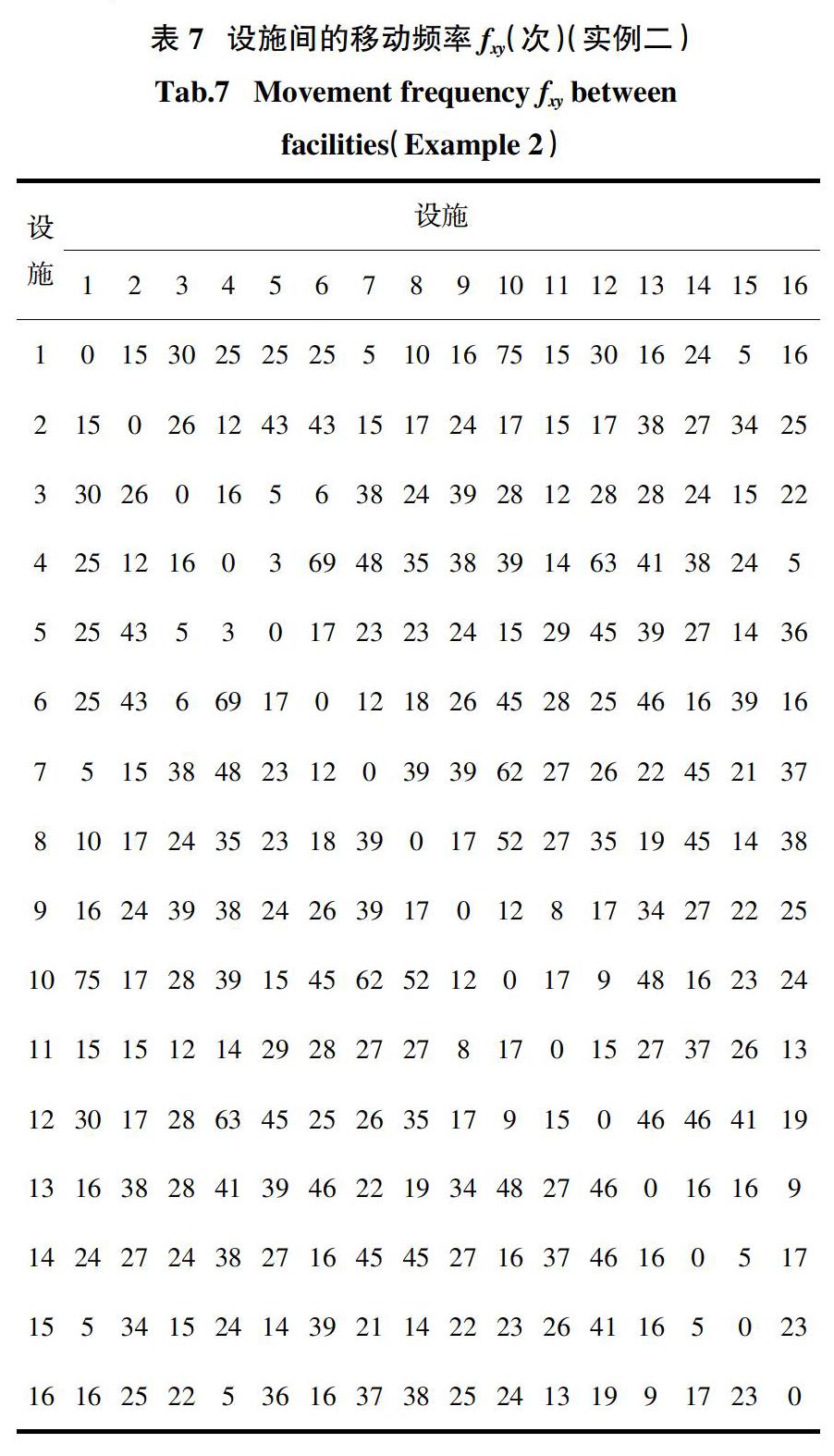
该施工现场设施布局优化问题的模型可根据公式（1）建立. 其中，设施间物流频次（一天内）参数fxy（x，y = 1，…，11）如表3所示，例如，设施1（现场办公室）与设施2（临时支架车间）一天内的物流频次为f12 = 5，设施6与设施8一天内的物流频次为f68 = 8. 位置间的距离参数dij（i，j = 1，…，11）如表4所示，例如，位置1与位置7间的距离为d17 = 47米，位置4与位置5间的距离为d45 = 7米. 在该案例的布局优化模型中，侧门（设施8）和正门（设施11）固定安排在位置1和位置10内，要求公式（1）增加约束条件δ8，1 = 1和δ11，10 = 1，对应的布局方案向量表示θ = [θ1，θ2，…，θ11]中要求元素θ8 = 1，θ11 = 10.

该设施布局优化问题需考虑将9个设施分配在9个位置，故问题的可行解（布局方案）个数为9！=362 880.通过枚举法可得到问题的最优目标函数值为6 273 m.针对本实例问题，基于TMCMC的建议优化算法的参数中，无量纲化常数g0取值10 000，样本变异系数取0.3.图2描述了基于TMCMC的建议优化算法一次典型求解过程（每一阶段的样本个数取100）中最优目标函数值随迭代阶段的变化，图3描述了该求解过程中温度参数随迭代阶段的变化.

为检验基于TMCMC的施工现场设施布局优化算法的稳定性，表5给出了针对案例问题的500次建议优化算法求解的统计结果. 作为对比，表5也提供了遗传算法（Genetic Algorithm，GA）的500次求解的统计结果.本文采用的遗传算法为双交叉算子遗传算法，其与传统遗传算法相比，更适用于组合优化问题，且性能更优[14]. 其交叉操作采用交叉掩码和部分映射杂交算子作为双交叉算子，既能保护优质染色体，又不影响劣质染色体的进化，从而提高种群的收敛速度.其变异操作采用染色体内部变异的方式，即随机选择染色体内的两个基因进行交换.考虑到计算资源对两种优化算法性能的影响，两种算法的迭代终止原则均取为迭代次数不超过20代.

由表5可知，当优化算法每代的样本数取50时，基于TMCMC的建议优化算法的500次独立运行结果中，有72.4%的频率可获得真实最优解（对应目标函数值6273 m），而基于GA的优化算法的相应频率仅为32.8%.当每代的样本数增加到100、150和200时，两种优化算法获得真实最优解的频率都随着样本数的增加而提高，且基于TMCMC的优化算法获得真实最优解的频率更高，这表明基于TMCMC的优化算法具有更好的求解稳定性.

此外，表5也提供了两种算法获得的最优解的目标函数值的统计结果（最大值、最小值、平均值及标准差）. 对比可知，在每代样本数相同的情况下，基于TMCMC的优化算法获得最优解的目标函数值的最大值（最差情况下）小于基于GA的优化算法的相应数值，且样本标准差更小，这再次验证了基于TMCMC的优化算法的求解稳定性. 同时，在每代不同样本数下两种算法的单次运行平均耗时如表5中的第8列所示.对比可见，在每代样本数相同的情况下，基于TMCMC的建议优化算法单次运行平均耗时更短，但性能（获取全局最优解的稳定性）更优，说明基于TMCMC的优化算法更为高效（与GA算法相比）.

3.2   工程实例二（16项临时设施）

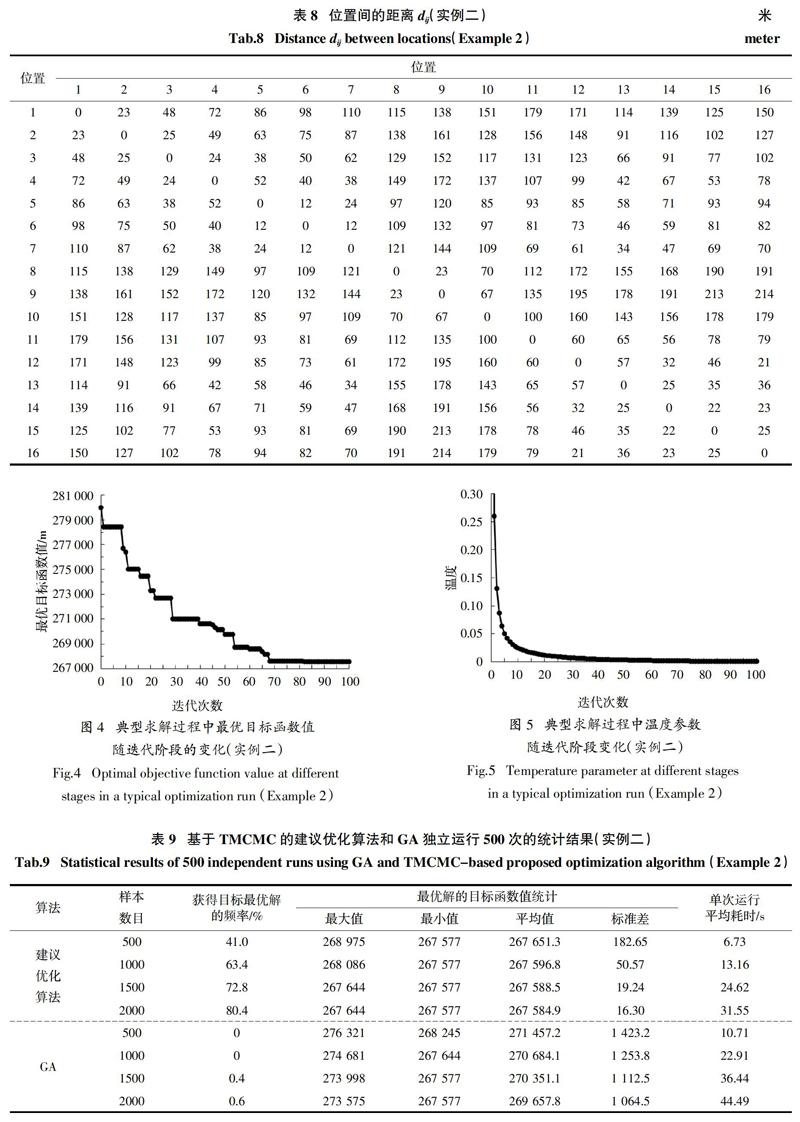
本实例来源于某房地产工程项目，该项目总建筑面积约17.88万m2，其中地上建筑面积12.88万m2，地下建筑面积5万m2. 在主体施工阶段需考虑将16个临时设施分配至16个预定位置内，同样假定每个预定位置都足以容纳任一临时设施. 16个临时设施的具体信息和编号如表6所示. 一天内临时设施间的物流频次如表7所示，所涉及的位置间的距离如表8所示. 因正门和侧门的位置预先已确定，分别分配在位置1（设施8，侧门）和位置10（设施11，正门）内.该优化问题需考虑将14个临时设施分配在14个位置，故问题的可行解个数为14！=8.718 × 1010.

针对本实例问题，基于TMCMC的建议优化算法的参数中，无量纲化常数g0取500 000，样本变异系数取值0.1.圖4描述了基于TMCMC的建议优化算法一次典型求解过程（每一阶段样本数取1 000）中最优目标函数值随迭代阶段的变化，图5描述了该求解过程中温度参数随迭代阶段的变化.为比较建议优化算法和GA算法的性能，表9给出了针对本实例问题的500次建议优化算法和GA算法求解的统计结果. 两种算法的迭代终止原则均取迭代次数不超过100代. 由于本实例问题可行解的个数过多（14！=8.718×1010），无法采用枚举法来得到问题的真实最优解，故采用考察中优化算法（建议优化算法和GA算法每代采用不同样本，独立运行500次）所有求出“最优解”中的最优者作为“真实全局最优解”，其目标函数值267 577（表9中第5列-最小值中的最小数）作为“真实最优目标函数值”，并以此作为比较建议优化算法和GA算法的基础.同时，与实例一的问题相比，实例二的设施布局优化问题中可行解的个数为实例一的240 240 （即14！/9！）倍，问题复杂程度急剧上升，故在建议优化算法和GA算法中每代的样本数取较大数值，即表9中的500、1 000、1 500、2 000.

通过对比表9和表5的结果可知，基于TMCMC的建议优化算法和GA算法在实例二中的求解统计结果不如实例一中的结果理想.但考虑到两个实例问题中差距巨大的可行解个数和复杂程度，上述的结果也较为合理. 同时，由表9可知，当每代的样本数取500时，基于TMCMC的建议优化算法的500次独立运行结果中，有41.0%的频率可获得“真实全局最优解”（对应目标函数值267 577 m），且其获得“真实全局最优解”的频率随着样本数的增加而提高. 当每代样本数取2 000时，其获得“真实全局最优解”的频率为80.4%. 作为对比，GA优化算法在每代样本数取500、1 000、1 500、2 000时获得“真实全局最优解”的频率几乎全部为0，最高值仅为0.6%.此外，由表9可知，在每代样本数相同的情况下，基于TMCMC的建议优化算法获得的最优目标函数值的平均值更接近2 675 577 m，且标准差大大小于GA算法的相应数值.由此可见，与GA算法相比，基于TMCMC的优化算法在获取全局最优解的稳定性上有较大的改进.同时，由表9中第8列两种算法的单次运行平均耗时的对比可见，与GA算法相比，基于TMCMC的建议优化算法计算效率更高，能够以更短的单次运行平均耗时获得更优的性能（获取全局最优解的稳定性）.

4   结   论

本文针对涉及较多设施的施工现场布局优化问题，基于TMCMC方法进行启发式优化算法的研究，主要研究结论如下：

1）在布局方案的向量表示下，可通过合理构造的概率分布函数，将施工现场设施布局优化问题转化为高维空间中的随机抽样问题，进而利用TMCMC方法来进行随机抽样、并获取最优解.

2）为适应离散型变量优化问题的不同特性，本文提出的启发式算法的框架基础需从原始TMCMC针对的连续型概率密度分布函数的随机取样转变为离散型概率分布函数的随机取样，进而需修改其中的马尔可夫链状态点的产生方法.

3）通过实例验证，与应用较广的GA算法相比，基于TMCMC的启发式优化算法在全局最优解的获取稳定性上有较大改进.

参考文献

[1]   YEH I C. Architectural layout optimization using annealed neural network[J]. Automation in Construction，2006，15（4）：531—539.

[2]    宋兴蓓. 基于BIM技术的施工现场动态布置研究[D].西安：长安大学经济与管理学院，2017：2—5.

SONG X B. The study of dynamic construction site layout based on BIM technology application[D]. Xi'an：School of Economics and Management，Chang'an University，2017：2—5. （In Chinese）

[3]    马筠强. 基于BIM的施工现场布置优化研究[D]. 哈尔滨：哈尔滨工业大学經济与管理学院，2016：1—6.

MA J Q. Research on construction site layout planning optimization based on BIM[D]. Harbin：School of Management，Harbin Institute of Technology，2016：1—6. （In Chinese）

[4]    TATE D M，SMITH A E. Unequal-area facility layout by genetic search [J]. IIE Transactions，1995，27（4）：465—472.

[5]    LIAO T W，EGBELU P J，SARKER B R，et al. Metaheuristics for project and construction management - A state-of-the-art review [J]. Automation in Construction，2011，20（5）：491—505.

[6]    LI H，LOVE P E D. Site-level facilities layout using genetic algorithms[J]. Journal of Computing in Civil Engineering，1998，12（4）：227—231.

[7]    ADRIAN A M，UTAMIMA A，WANG K J. A comparative study of GA，PSO，and ACO for solving construction site layout optimization [J]. KSCE Journal of Civil Engineering，2015，19（3）：520—527.

[8]    BECK J L，AU S K. Bayesian updating of structural models and reliability using Markov chain Monte Carlo simulation[J]. Journal of Engineering Mechanics，2002，128（4）：380—391.

[9]   CHING J，CHEN Y C. Transitional Markov chain Monte Carlo method for Bayesian model updating，model class selection and model averaging[J]. Journal of Engineering Mechanics，2007，133（7）：816—832.

[10]  KIRKPATRICK S，GELATT C D，VECCHI M P. Optimization by simulated annealing[J]. Science，1983，220（4598）：671—680.

[11]  WANG J，KATAFYGIOTIS L S. Reliability-based optimal design of linear structures subjected to stochastic excitations[J]. Structural Safety，2014，47（2）：29—38.

[12]  WANG J，KATAFYGIOTIS L S，NOORI M N. Reliability-based optimal structural design using transitional Markov chain Monte Carlo [C]// Proceeding of the Asian-Pacific Symposium on Structural Reliability and its Applications（APSSRA 2008）. Hong Kong：HKUST，2008：239—245.

[13]  HASTINGS W K. Monte Carlo sampling methods using Markov chains and their applications[J]. Biometrika，1970，57（1）：97—109.

[14]  WONG C K，FUNG I W，TAM C M. Comparison of using mixed-integer programming and genetic algorithms for construction site facility layout planning[J]. Journal of Construction Engineering and Management，2010，136（10）：1116—1128.