考虑剪应力作用的有限土体被动土压力分析

徐日庆 徐叶斌

摘   要：以挡土墙后有限范围砂土为研究对象，建立挡土墙位移与内、外摩擦角的关系，假定墙后土体为圆弧形拱，并考虑层间剪应力，采用多道滑裂面假设下得到的破裂面角与被动土压力系数，推导了有限土体的被动土压力解，该公式也可退化为半无限土体的被动土压力解. 与模型试验相比，所提理论解与试验值吻合较好，证明了解析解的合理性. 参数分析表明：考虑层间剪应力下不影响被动土压力的合力，但会使其合力作用点升高;被动土压力随土体宽高比减小呈现先变化不大后急剧增加的趋势;被动土压力合力随内摩擦角增加呈单增趋势，而合力作用点则随之降低.

关键词：被动土压力;薄层单元法;有限土体;层间剪应力;土拱效应

中图分类号：TU 472                                文献标志码：A

文章编号：1674—2974（2020）09—0076—09

Abstract：Taking the sand soil in the limited range behind the retaining wall as the object， the relationship between the retaining wall displacement  and the internal and external friction angles is established. Assuming that the earth behind the wall is arc-shaped and considering the shear stress between the soil layers， the angle of fracture surface and passive earth pressure coefficient under the hypothesis of multichannel slip surfaces are adopted， and then the theoretical formula of passive earth pressure with limited soil is derived. It can also be degenerated into the solution of passive earth pressure with semi-infinite soil. Compared with the model test， the proposed theoretical solution is in good consistency with the experimental values， which verifies the rationality of the analytical solutions. Parameter analysis shows that： considering the inter-layer shear stress， the total value of passive earth pressure is not influenced， while the position of action point is higher. The passive earth pressure changes little at first and then increases significantly with the decrease of the soil aspect ratio. With the increase of the internal friction angle， the resultant of passive earth pressure increases while the position of action point is lower.

Key words：passive earth pressure;thin-layer element method;finite soil;inter-laminar shear stress;soil-arching effect

挡土墙后土压力的计算理论由来已久，经典的朗肯土压力与库伦土压力虽被广泛采用，但均未考虑到墙土摩擦对应力状态的影响与土体单元的应力偏转，且两者都为线性解，与实际情况差距较大，存在明显的局限性，虽然理论简单但无法应用于复杂情况. 目前土压力的求解大多采用薄层单元法分析，土压力分布曲线具有很强的非线性. 此外大部分土压力理论均假定挡土墙后的土压力处于理想状态，而实际上并非如此，一方面是由于随着城市地下空间的蓬勃发展，基坑挡土墙后土体并不能完全满足半无限土体的条件，相比于半无限土体，有限土体对基坑挡土墙的主动土压力会偏小[1-5]，而被动土压力则会偏大许多[6-7];另一方面，基坑挡土墙的位移往往未达到极限状态，土体的内外摩擦角未能完全发挥，直接采用极限状态参数并不合理. 因此有必要对非理想状态的被动土压力进行深入研究，以建立更完善的被动土压力理论，用以指导相关的基坑工程挡土墙设计.

对于非理想状态的被动土压力，为考虑非极限状态的影响，徐日庆等[8]引入挡土墙位移与摩擦角发挥值的关系，宋飞等[9]进一步考虑密砂的强度变化特性对被动土压力的影响，推导了砂土在非极限状态下的被动土压力解，能够从一定程度反映挡土墙后的被动土压力值，但其解均为线性，可视为朗肯解或库伦解的一种推广，具有一定的局限性. 徐明等[10]采用离散元方法研究了大颗粒粒径混合体的主动土压力，得到了主动土压力随粒径尺寸的变化规律. 竺明星等[11]基于双土拱效应推导了砂性土滑坡中抗滑排桩的滑坡推力解，分析表明桩身滑坡推力與滑坡倾角、砂土内摩擦角和桩间距比值有关. 应宏伟等[5-6]对狭窄基坑下砂土的主动与被动土压力进行了研究，并通过ABAQUS进行数值模拟提出对于有限土体其会出现多道潜在滑裂面，其中主动土压力呈“Z”形，被动土压力呈“X”形，由此推导得到的理论解表明：对于被动土压力，有限土体下破裂面夹角随宽高比减小有所增大，被动土压力系数随宽高比减小而增加，且增幅快速提升.

为了考虑土体单元应力偏转的影响，引入土拱效应求解土压力具有重要意义，1936年Terzaghi[12]通过活动门试验首次证明了土拱效应的存在，土拱效应是土体在自重与荷载作用下产生不均匀变形，而使得一定范围内土体出现应力重分布. 侯键等[13]、朱建明等[14]与周晓龙等[15]分别考虑了土拱效应的影响，对理想状态下砂土与黏土的被动土压力进行了推导，朱建明等[14]指出对于被动土压力，土拱效应随墙体倾角增大而增强，合力作用点高度也随之降低;周晓龙等[15]则提出随外摩擦角与内摩擦角比值的增大土拱效應逐渐增强，但上述研究均未考虑层间剪应力的影响，这是不合理的. 对土体单元进行受力分析，剪应力只有在主应力作用面才为零，而考虑土拱作用下主应力将发生偏转，因此应当考虑层间剪应力的影响. 刘忠玉等[16-17]研究了层间剪应力对主动土压力的影响，结果表明考虑层间剪应力对土压力合力不产生影响，但会使得主动土压力作用点有所降低.

通过上述讨论可知目前对于临近地下室的被动土压力研究较少，还未有考虑土层层间剪应力的影响，有待于进一步的研究. 本文在前人研究的基础上，以平动挡土墙后有限范围砂土为研究对象，考虑非极限状态下的土拱效应与层间剪应力，采用多滑裂面假设下得到的破裂面夹角与被动土压力系数，并将有限土体分为两个分离体，采用薄层单元法进行受力分析，得到了有限土体的被动土压力理论解，并分析参数变化对被动土压力的影响，可为相关工程设计提供一定参考.

1   有限土体被动土压力推导

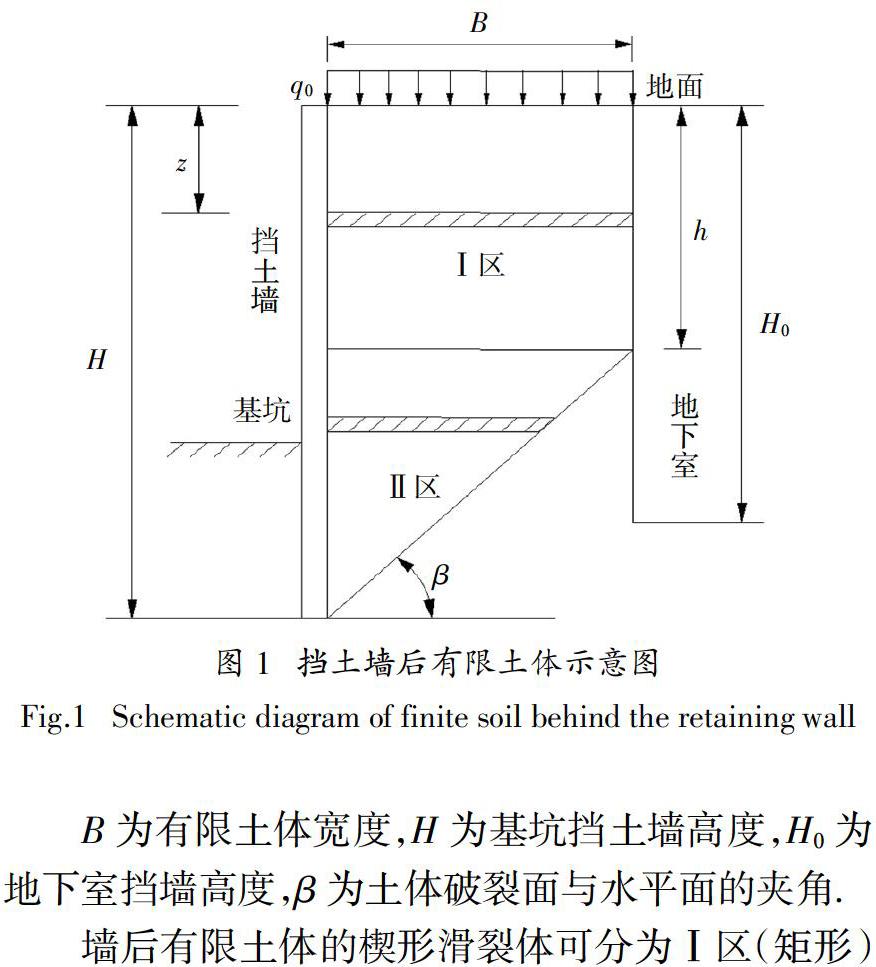
由于研究对象为基坑挡土墙后的有限土体，则应有土体破裂面与地下室挡墙交点到地面的距离h > 0，如图1所示.

B为有限土体宽度，H为基坑挡土墙高度，H0为地下室挡墙高度，β为土体破裂面与水平面的夹角.

墙后有限土体的楔形滑裂体可分为Ⅰ区（矩形）与Ⅱ区（三角形）两个分离体进行分析. 对于Ⅰ区，其薄层单元宽度固定为B;对于Ⅱ区，土体薄层单元宽度为Bz =（H - z）cot β. 当h = 0时，墙后土体只有Ⅱ区，即与半无限土体相同.

为了简化理论推导，可做如下假设：

其中h值为：

1）墙后砂土为单一土层，其内摩擦角为φ，土体与基坑挡土墙和地下室挡土墙之间的外摩擦角分别为δ和α.

2）地下室挡墙不产生位移，基坑挡土墙位移模式为平动，其水平位移设为Sz .

3）墙顶后土体与挡土墙在同一水平线上，且上部附加荷载均匀分布，设为q0 .

4）墙后破裂面与地下室外墙相交，即有H0 > h.

5）墙后砂土的土拱为大主应力拱，土拱形状为圆弧形.

1.1   非极限状态下的摩擦角

非极限状态是指挡土墙逐渐产生位移而使其后土体的摩擦角逐渐发挥的某一状态.

对于内摩擦角发挥值φm和外摩擦角发挥值δm，在平动模式下，Fang等[18]与Matsuzawa等[19]分别通过模型试验与数值模拟得出φ与δ随位移呈线性增长，然后保持一恒定值的结论，其取值均可采用Chang[20]提出的公式.

对于内摩擦角发挥值φm，其值为：

式中：土的内摩擦角初始值φ0可采用Federico等[21]的研究成果，取φ0 = 0.64φ. η为墙体位移比，其值为η = Sz /Sp，Sz为某被动状态下墙体的位移，Sp为被动极限状态下墙体的位移.

对于外摩擦角发挥值δm，其值为：

初始外摩擦角δ0可取为φ/2[19]，δ为实测值，在缺乏资料时可取δ = 2φ/3[20].

对于地下室挡土墙和土体之间的外摩擦角αm也有相同的结论.

1.2   非极限状态下土拱效应分析

1.2.1   Ⅰ区土拱效应分析

图2给出了挡土墙后Ⅰ区土体的大主应力轨迹线.

由图2中几何关系可知：

图3所示为挡土墙后土体的应力莫尔圆.

由图中的应力莫尔圆可求得有限土体两侧的主应力偏转角分别为：

微分单元体竖向应力和水平向应力分别为

式中：Kpm为朗肯被动土压力系数，其值为

1.2.2   Ⅱ区土拱效应分析

图4所示为挡土墙后Ⅱ区土体的大主应力轨迹线.

由图4中几何关系可知：

1.3   层间剪应力系数

1.3.1   Ⅰ区层间剪应力系数

对于土层层间剪应力，由章瑞文等[22]与图3可求得其值为

1.3.2   Ⅱ区层间剪应力系数

对于Ⅱ区的土体，考虑土拱效应下的平均剪应力为

1.4   破裂面角与被动土压力增强系数

对于破裂面角与被动土压力系数，本文参照应宏伟等[6]文中方法，假定有限宽度土体将会出现多道潜在滑裂面，其计算模型如图5所示.

当基坑挡土墙后为半无限土体时，仅有一道滑裂面，即满足

记β1为第一道滑裂面夹角，作用在h1上的被动土压力合力为F1，相应的被动土压力系数为K1. 按照经典库伦理论，使被动土压力系数K1达到极小值Kc的滑裂面角β1即为库伦滑裂面角βc，其中Kc与βc分别为

当土体宽高比减小刚进入有限土体时，将产生第二道滑裂面，此时满足

记β2为第二道滑裂面夹角，作用在h2上的被动土压力合力为F2，相应的被动土压力系数为K2.

取梯形滑裂体进行分析，其受力分析如图6所示.

其水平向与竖向的受力平衡方程如下：

对于楔形体满足库伦理论的求解条件，由此可知此时β2 = βc，K2 = Kc，代入式（23），并将K1对ξ1进行求导，导数为零的点即为被动土压力系数K1的极值点，由此也可得到相应的最危险滑裂面角β1 .

式中：

当土体宽度进一步减小时，将使n2也不再满足n2 ≥ nc的条件，此时将产生更多的滑裂面，假设共产生n组滑裂面，第i組滑裂面底部相应的深度为hi，相应的滑裂面倾角为βi，被动土压力合力为Fi .

设半无限土体下得到的被动土压力系数和破裂面角为Kc与βc，在有限土体B宽度下得到的被动土压力系数和破裂面角为KB与βB，令有限土体被动土压力增强系数 为

1.5   隔离体静力平衡方程推导

1.5.1   Ⅰ区静力平衡方程

取Ⅰ区薄层单元进行受力分析，如图7所示.

根据图7的受力分析图，分别建立竖向及水平向微分方程为

1.5.2   Ⅱ区静力平衡方程

取Ⅱ区薄层单元进行受力分析，如图8所示.

根据图8的受力分析，分别建立竖向及水平向微分方程为

1.6   挡土墙后侧向土压力

考虑被动土压力增强系数后，侧向土压力为

1.7   被动土压力合力及其作用点位置

挡土墙后被动土压力合力作用点距离挡土墙底部为hp，其值可按下式计算

2   模型试验对比分析

应宏伟等[7]对砂土的被动土压力进行了模型试验研究. 模型试验参数如下：填土重度γ = 14.6 kN/m3，摩擦角φ = 35°，墙土间摩擦角δ = 16.57°，填土表面均布荷载q0 = 0，挡土墙后土体高度为H = 0.525 m. 当土体宽高比为B/H = 10/3，可得B > H cot β，即为半无限土体;当墙后土体宽高比为B/H = 4/5时，可得B < H cot β，即为有限土体. 具体试验装置和试验过程详见文献[7].

图9给出了半无限土体和有限土体的理论解与试验值的对比图，其中应宏伟理论解与侯键理论解详见文献[6]与[13]. 结果表明：首先，无论是半无限土体还是有限土体，与侯键解和应宏伟解相比较，本文理论解均表现为上部偏大，而下部偏小一些，这可能与本文考虑了土层层间剪应力有关. 总体上本文解能较好地与试验值相吻合，验证了本文方法的合理性. 其次，所得被动土压力理论解在底部相比试验值会偏大，这可能是由于土体底部为模型箱而带来边界效应的影响.

3   参数分析

为了研究φ、B/H和层间剪应力对被动土压力大小及分布的影响，本文通过算例来讨论各因素的影响规律. 参数统一取值为：H = 10 m，φ = 30°，δ = α = 2φ/3，γ = 16 kN/m3，q0 = 0 kPa，η = 1.0，土体宽度B > H cot β，即为半无限土体. 在考虑相关参数影响时再另取值.

3.1   层间剪应力的影响

图10给出了层间剪应力和土拱效应对被动土压力的影响，从中可以得出：无论是被动极限状态还是非极限状态，考虑土拱效应均会使被动土压力的分布非线性更强，而考虑层间剪应力下被动土压力分布总体会有所抬高，而对其合力不产生影响. 其中，在挡土墙上部，考虑层间剪应力作用的被动土压力比未考虑层间剪应力的要大，而挡土墙下部则反之. 这是由于在平移模式下，被动土压力的层间剪应力方向与主动土压力相反，导致应力由土体底部向表面传递. 土层层间剪应力作为土体的内力，由作用力和反作用力的关系可知，其仅会影响土体被动土压力的分布，而不影响被动土压力的合力.

3.2   宽高比的影响

图11给出了不同内摩擦角下被动土压力合力随土体宽高比变化的规律. 由图可知，对于不同内摩擦角，随着土体宽高比的减小，被动土压力合力均表现为初期略有减小后增大，达到临界点之后呈急剧增长的趋势. 且土体内摩擦角越小，土体由半无限土体进入到有限土体的B/H值越小. 不难解释，土体内摩擦角越小，则破裂面角越大，有限土体的临界值B/H也就越小. 土压力合力的变化规律则是由于土体宽高比刚进入有限土体时，滑裂区土体减少引起被动土压力减小，而被动土压力系数初期变化不大;当土体宽高比进一步减小时，由于地下室挡土墙的约束导致被动土压力系数迅速增大，从而使被动土压力呈现急剧增长的趋势.

3.3   内摩擦角的影响

图12给出了内摩擦角φ对被动土压力的影响，由此可知：无论是有限土体还是半无限土体，被动土压力合力均随φ的增大而逐渐增大，且变化幅度不断增大;合力作用点则随φ的增大逐渐降低，半无限土体作用点高度始终高于有限土体. 不难解释，与主动土压力随φ的增大而减小不同，由于被动土压力的两侧摩擦力是向下的，因此内摩擦角增加会导致侧向土压力增大. 同样地，在内摩擦角一定时，外摩擦角与内摩擦角比值增大也会引起侧向土压力增大. 对于作用点高度，由于有限土体与半无限土体的被动土压力差值在下部显著大于上部，因此使得有限土体作用点高度偏低.

4   结   论

本文通过考虑土拱效应、土层层间剪应力和土体宽高比的影响，推导了有限土体的被动土压力解，该公式也可退化为半无限土体的被动土压力解. 与模型试验结果和前人理论解相对比，本文理论解能更好地与试验值吻合，证明了本文解的合理性. 参数分析表明：

1）对于被动土压力，层间剪应力使得其合力作用点有所抬高，而对其合力不产生影响，层间剪应力系数的数值取决于内外摩擦角与破裂面角.

2）随着宽高比的增加，被动土压力合力呈现先变化不大后急剧增长的趋势，且土体内摩擦角越小，土体由半无限土体进入到有限土体的B/H值越小.

3）无论是有限土体还是半无限土体，随着内摩擦角的增加，均表现为被动土压力合力逐渐增大，合力作用点逐渐降低.

目前关于土体宽高比对被动土压力影响的理论与试验还较少，有待于更多的理论研究与试验结果来更好地揭示其影响规律.

参考文献

[1]    岳树桥，左人宇，陆钊. 相邻基坑有限宽度土条主动土压力的计算[J]. 岩土力学，2016，37（7）：2063—2069.

YUE S Q，ZUO R Y，LU Z. A method for calculating active earth pressure of soil piece with a finite width between adjacent foundation pits[J]. Rock and Soil Mechanics，2016，37（7），2063—2069.（In Chinese）

[2]    杨明辉，戴夏斌，赵明华，等. 墙后有限宽度无黏性土主动土压力试验研究[J]. 岩土工程学报，2015，38（1）：131—137.

YANG M H，DAI X B，ZHAO M H，et al. Experimental study on active earth pressure of cohesionless soil with limited width behind retaining wall[J]. Chinese Journal of Geotechnical Engineering，2015，38（1）：131—137.（In Chinese）

[3]    王闫超，晏鄂川，陆文博，等. 无黏性有限土体主动土压力解析解[J]. 岩土力学，2016，37（9）：2513—2520.

WANG Y C，YAN E C，LU W B，et al. Analytical solution of active earth pressure for limited cohesionless soils[J]. Rock and Soil Mechanics，2016，37（9）：2513—2520.（In Chinese）

[4]    马平，秦四清，钱海涛. 有限土体主动土压力计算[J]. 岩石力学与工程学报，2008，27（S1）：3070—3074.

MA P，QIN S Q，QIAN H T. Calculation of active earth pressure for limited soils[J]. Chinese Journal of Rock Mechanics and Engineering，2008，27（S1）：3070—3074.（In Chinese）

[5]    应宏伟，黄东，谢新宇. 考虑邻近地下室外墙侧压力影响的平动模式挡土墙主动土压力研究[J]. 岩石力学与工程学报，2011（S1）：2970—2978.

YING H W，HUANG D，XIE X Y. Study of active earth pressure on retaining wall subject to translation mode considering lateral pressure on adjacent existing basement exterior wall[J]. Chinese Journal of Rock Mechanics and Engineering，2011（S1）：2970—2978.（In Chinese）

[6]    应宏伟，郑贝贝，谢新宇. 狭窄基坑平动模式刚性挡墙被动土压力分析[J]. 巖土力学，2011，32（12）：3755—3762.

YING H W，ZHENG B B，XIE X Y. Study of passive earth pressures against translating rigid retaining walls in narrow excavations[J]. Rock and Soil Mechanics，2011，32（12）：3755—3762.（In Chinese）

[7]    应宏伟，张金红，王小刚，等. 有限土体刚性挡墙平动模式被动土压力试验研究[J]. 岩土工程学报，2016，38（6）：978—986.

YING H W，ZHANG J H，WANG X G，et al. Experimental analysis of passive earth pressure against rigid retaining wall under translation mode for finite soils[J]. Chinese Journal of Geotechnical Engineering，2016，38（6）：978—986.（In Chinese）

[8]    徐日庆，李昕睿，朱剑锋. 刚性挡土墙平动模式下中间被动土压力的计算[J]. 浙江大学学报（工学版），2010，44（10）：2005—2009.

XU R Q，LI X R，ZHU J F. Calculation of inter-mediate passive earth pressure against rigid retaining wall of translation mode[J]. Journal of Zhejiang University （Engineering Science），2010，44（10）：2005—2009.（In Chinese）

[9]    宋飞，张建民. 考虑挡墙位移效应的被动侧土压力计算方法[J]. 岩土力学，2011，32（1）：151—157.

SONG F，ZHANG J M. Computational method of earth pressure at passive side considering wall displacement effect[J]. Rock and Soil Mechanics，2011，32（1）：151—157.（In Chinese）

[10]  徐明，王蕴佳，沈志平，等. 基于离散元的溶塌巨石混合体主动土压力研究[J]. 湖南大学学报（自然科学版），2018，45（S1）：128—132.

XU M，WANG Y J，SHEN Z P，et al. Study on active earth pressure of talus based on discrete element method[J]. Journal of Hunan University（Natural Sciences），2018，45（S1）：128—132.（In Chinese）

[11]  竺明星，卢红前，戴国亮，等. 基于双土拱效应的砂性土滑坡中抗滑排桩滑坡推力研究[J]. 湖南大学学报（自然科学版），2018，45（S0）：8—13.

ZHU M X，LU H Q，DAI G L，et al. Research on landslide thrust of anti-slide row piles in sandy slope with consideration of double soil-arching effects[J]. Journal of Hunan University（Natural Sciences），2018，45（S0）：8—13.（In Chinese）

[12]  TERZAGHI K. Theoretical soil mechanics[M]. New York：John Wiley and Sons，1943：66—76.

[13]  侯键，夏唐代，孔祥冰，等. 基于土拱效应原理求解挡土墙被动土压力[J]. 岩土力学，2012，33（10）：2296—3000.

HOU J，XIA T D，KONG X B，et al. Passive earth pressure on retaining walls calculated by principle of soil arching effect[J]. Rock and Soil Mechanics，2012，33（10）：2296—3000.（In Chinese）

[14]  朱建明，趙琦. 考虑土拱效应的挡土墙主动土压力与被动土压力统一解[J]. 岩土力学，2014，35（9）：2501—2505.

ZHU J M，ZHAO Q. Unified solution to active earth pressure and passive earth pressure on retaining wall considering soil arching effects[J]. Rock and Soil Mechanics，2014，35（9）：2501—2505.（In Chinese）

[15]  周晓龙，马亢，钱明，等. 黏性土填料下考虑土拱效应的挡土墙被动土压力计算[J]. 岩土力学，2014（S1）：245—250.

ZHOU X L，MA K，QIAN M，et al. Calculation of passive earth pressures on retaining wall considering soil arching effects of backfill clayey soil[J]. Rock and Soil Mechanics，2014（S1）：245—250. （In Chinese）

[16]  刘忠玉，陈捷，李东阳. 考虑剪应力作用的刚性挡土墙主动土压力分析[J]. 岩土力学，2016，37（9）：2443—2450.

LIU Z Y，CHEN J，LI D Y. Calculation of active earth pressure against rigid retaining wall considering shear stress[J]. Rock and Soil Mechanics，2016，37（9）：2443—2450.（In Chinese）

[17]  刘忠玉，陈捷. 平动模式下考虑剪应力作用的刚性挡土墙主动土压力计算[J]. 岩土工程学报，2016，38（12）：2254—2261.

LIU Z Y，CHEN J. Active earth pressure against rigid retaining wall considering shear stress under translation mode[J]. Chinese Journal of Geotechnical Engineering，2016，38（12）：2254—2261.（In Chinese）

[18]  FANG YUNG-SHOW，ISHIBASHI ISAO. Static earth pressures with various wall movements[J]. Journal of Geotechnical Engineering，1986，112（3）：317—333.

[19]  MATSUZAWA H，HAZARIKA H. Analyses of active earth pressure against rigid retaining walls subjected to different modes of movement[J]. Soils and Foundations，1996，36（3）：51—65.

[20]  CHANG M F. Lateral earth pressures behind rotating walls[J]. Canadian Geotechnical Journal，1997，34（2）：498—509.

[21]  FEDERICO A，ELIA G，GERMANO V. A short note on the earth pressure and mobilized angle of internal friction in one-dimensional compression of soils[J]. Journal of Geo Engineering，2008，3（1）：41—46.（In Chinese）

[22]  章瑞文，徐日庆. 土拱效应原理求解挡土墙土压力方法的改进[J]. 岩土力学，2008，29（4）：1057—1060.

ZHANG R W，XU R Q. Solution of problem of earth pressure on retaining wall calculated by method of soil arching effect[J]. Rock and Soil Mechanics，2008，29（4）：1057—1060.（In Chinese）