基于兰彻斯特方程的有人/无人协同作战
毛炜豪,刘网定,卢洪涛
(陆军指挥学院,江苏 南京 210045)
现代战场上,战场无人机、机器人等无人化、智能化武器的成建制使用,已经成为现实[1]。2015年12月,叙利亚政府军在俄军战斗机器人的强力支援下,成功攻占“伊斯兰国”武装分子控制的拉塔基亚754.5高地[2]。美国陆军也组建了有人/无人混编陆航营,为战斗航空旅的攻击直升机营编配24架AH-64E和3个RQ-7R(V2)“影子”200无人机系统排,使其具备有人/无人机的协同作战能力[3]。美空军还开始量产“忠诚僚机”,1架F-35能指挥3至6架XQ-58A无人机协同作战[4]。俄、美对于无人化装备的作战运用说明无人化装备通过接收指控信号可实现“人机一体”,发挥与有人装备相同甚至更强的作战效能。本文尝试结合现代战争无人化和智能化特点,根据有人/无人协同战术运用方式,通过加入新型变量、调整方程结构、修正方程因子等方法,构建基于兰彻斯特方程的“有人/无人协同”作战模型,并通过实例加以验证,探索对于无人化作战集群的最佳战术运用方式。
1 兰彻斯特方程
兰彻斯特方程[5]是在一些假设的前提下描述损耗过程的微分方程组,主要可用来测算兵力和武器装备的损耗,主要有三个定律:第一线性律、第二线性律和平方律。下面以平方律为例,从战斗力影响因子的角度对其进行简要介绍和再解读,这也是构建基于兰彻斯特方程的“有人/无人协同”作战模型的逻辑起点。
1.1 兰彻斯特平方律
兰彻斯特平方律又称兰彻斯特直接开火模型。在使用火炮或其他兵器集中射击时,按平均数量计算,每一件武器在特定时间内都会有效地命中一定数量的目标,因此,在单位时间内消灭敌方目标的数量,就与射击一方兵力或武器的数量成正比。于是得到了如下的平方律方程。兵力损耗模型为
(1)
式中,x、y为红、蓝双方在t时刻的瞬时兵力(或剩余兵力);α、β分别表示红方、蓝方的平均战斗效能。
由式(1)推导可得
(2)
1.2 战斗力影响因子分析
现代战争中,进攻方对于防御方发起的地面“冲锋”或两栖“突击上陆”行动,是打破敌防御体系的关键行动,往往是整个作战进程的高潮部分,并决定攻防战斗的最终结果。因此,双方指挥员往往投入大量兵力兵器,力求赢得这一作战阶段的胜利。由于近距离战斗时,兵力规模因子对于战斗力的影响大于单兵战斗效能因子,因此,指挥员往往采取“集中兵力”的方式,对敌形成局部优势,进而,破击敌整体防御体系。这也是“集中兵力”用兵原则背后的数学原理。
使用无人机、机器人等无人化作战集群参与地面或两栖作战,尤其是在发起冲锋或突击上陆等攻坚作战阶段,具有如下优势:第一,在进攻时,无人机、机器人等装备机动速度快、自带传感器和火控系统,可以更加高效地对防御方实施侦测和打击;第二,无人化武器装备与士兵协同作战,相当于增加了进攻方的兵力,这在近距离战斗中可显著增强进攻方的整体战斗力;第三,防御方对于这类无人化武器目标的打击,减少了进攻方的兵力消耗,相当于降低了防御方的兵力优势。综上所述,使用无人化装备集群可显著增强整体战斗力,并削弱对方兵力优势。
2 “有人/无人协同作战”混合模型
为了充分验证有人/无人协同作战的整体效能,下面尝试构建三类不同的交战模型。为了便于对比,分别对红方“有人/无人相对独立作战”与蓝方“传统有人作战”、红方“有人/无人密切协同作战”与蓝方“传统有人作战”、红方“有人/无人密切协同作战”与蓝方“有人/无人相对独立作战”三种情况构建数学模型,并进行分析。由于“有人/无人协同作战”中,无人作战集群依赖于有人作战集群而存在,因此,在模型中将无人作战集群数量设置为兵力数量的一定比例。
2.1 交战一方“有人/无人相对独立作战”模型
交战一方“有人/无人相对独立作战”模型设想红蓝双方交战,其中,红方为“有人/无人相对独立作战”,而蓝方为“传统有人作战”。所谓“有人/无人相对独立作战”是指在作战过程中,红方士兵与无人机和战斗机器人集群共享战场情报,但分别相对独立作战。如,在空间上处于不同的作战地域,或在时间上参与不同的作战阶段,以遂行不同的作战任务。例如,叙政府军在俄军战斗机器人的支援下攻占拉塔基亚754.5高地[6],先由机器人实施“火力精确拔点”,然后,叙政府军实施战场扫荡,就属于有人/无人相对独立作战的类型。这种协同方式有利于发挥有人集群和无人化集群各自的优势,但缺点在于二者之间仅存在有限的协同,容易被各个击破。
由此,构建模型为
(3)
式中,Q为蓝方侦察效能(即红方被全部发现的概率,因此,Q≤1),P1、P2分别为红方有人和无人化集群的侦察效能(即蓝方分别被红方有人集群和无人化集群发现的概率,因此,P1+P2≤1);β为蓝方单兵作战效能,α1、α2分别为红方单兵和单个无人装备的作战效能;γ为无人化装备数量与兵力数量的比例,即无人化装备数量为γx(t);x(t)、y(t)分别为红方、蓝方在t时刻的剩余兵力。由式(3)可推导出
(4)
2.2 交战一方“有人/无人密切协同作战”模型
类似地,红蓝交战,设想红方为“有人/无人密切协同作战”,而蓝方为“传统有人作战”。所谓“有人/无人密切协同作战”,是指在作战过程中,红方士兵与无人化集群密切协同作战,如在空间上处于同一作战地域,或在时间上参与相同的作战阶段,共同遂行同一作战任务[7]。例如,美军演习中,隐形战机和无人机前出协同突防,并通过“战斗云”共享战场态势。首先,遥控X-47B型无人机实施多波次突击,压制敌防空系统,一旦取得局部制空权,常规战机迅速跟进,对敌目标实施精确火力打击[8]。这种协同方式有利于快速共享战场情报,并充分发挥有人集群和无人化集群协同作战的优势,但缺点在于目前协同难度较大,尤其在地面作战中,要确保无人化装备具有强大的自组织和敌我识别能力,操作人员也要具备一定的专业素养,避免在协同作战时造成误伤[4]。
由此,构建模型为
(5)
类似式(3),上式中,Q为蓝方侦察效能(Q≤1),P1、P2分别为红方有人和无人化集群的侦察效能(P1+P2≤1);β为蓝方单兵作战效能,α1、α2分别为红方单兵和单个无人装备的作战效能;γ为无人化装备数量与兵力数量的比例,即无人化装备数量为γx(t);x(t)、y(t)分别为红方、蓝方在t时刻的剩余兵力。由式(5)可推导出
(6)
2.3 两种协同方式对战混合模型
设想红方为“有人/无人密切协同作战”,而蓝方为“有人/无人相对独立作战”。由此,构建模型为
(7)
类似地,上式中,Q1、Q2分别为红方有人和无人化集群的侦察效能(Q1+Q2≤1),P1、P2分别为红方有人和无人化集群的侦察效能(P1+P2≤1);β1、β2分别为蓝方单兵和单个无人装备的作战效能,α1、α2分别为红方单兵和单个无人装备的作战效能;v为蓝方无人化装备数量与兵力数量的比例,即无人化装备数量为vy(t);γ为红方无人化装备数量与兵力数量的比例,即无人化装备数量为γx(t);x(t)、y(t)分别为红方、蓝方在t时刻的剩余兵力。由式(7)可推导出
(8)
令Q1=P1,Q2=P2;β1=β2,α1=α2;且v=γ,y0=x0,则可推导出
(9)
式(9)中,由于右侧始终为正值,因此,红方必胜。这就说明,在红蓝双方均采取有人/无人协同作战,且双方侦察效能、作战效能、兵力规模完全一致的情况下,采取“有人/无人密切协同”作战方式,必然能够击败“有人/无人相对独立”作战方式。
3 仿真实例
为了进一步验证三类模型,使结果对比更加直观,本文使用Matlab进行仿真验证。由于有人/无人作战集群在自主性、协同性、侦察效能、作战效能、抗毁伤能力等方面各有优势,很难逐一量化比较,为了聚焦核心问题,即对比分析有人/无人作战集群不同协同方式带来的影响,在下面的实例中,均假设有人/无人作战集群的侦察效能、作战效能完全一致。
3.1 交战一方“有人/无人相对独立作战”模型
假设红蓝对战,其中,红方为有人/无人作战集群,士兵与无人化装备的侦察效能、作战效能完全一致,红方拥有无人作战集群,但兵力处于劣势;蓝方为有人作战集群,兵力处于优势。在“有人/无人相对独立作战”条件下:
1)红方兵力与无人集群数量之和等于蓝方兵力时,令红方初始兵力为500人,蓝方初始兵力为1 000人,侦察效能均为0.5,作战效能均为0.6,红方无人作战集群作战效能为0.5,侦察效能为0.6,数量比例为1(无人化装备等于士兵数量)。即x0=500,y0=1 000,Q=P1=0.5,α1=β=0.6,P2=0.5,α2=0.6,γ=1。如图1所示。

图1 有人/无人相对独立作战模型(红方有人/无人集群数量相等,且二者之和等于蓝方兵力)
2)令红方初始兵力为600人,蓝方初始兵力为1 000人,侦察效能均为0.5,作战效能均为0.6,红方无人作战集群作战效能为0.5,侦察效能为0.6,数量比例为0.67(即无人化装备数量约为400)。即x0=600,y0=1 000,Q=P1=P2=0.5,β=α1=α2=0.6,γ=0.67。如图2所示。
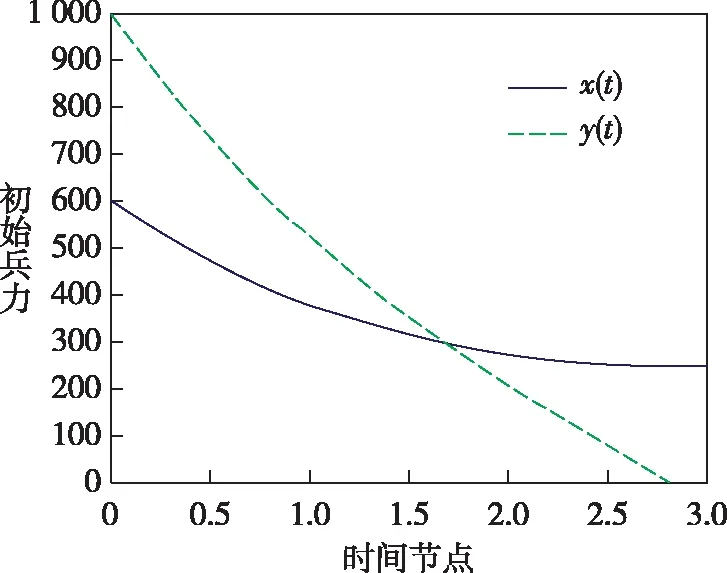
图2 有人/无人相对独立作战模型(红方兵力增加、无人集群减少,且有人/无人集群数量之和等于蓝方兵力)
3)令红方初始兵力为400人,蓝方初始兵力为1 000人,侦察效能均为0.5,作战效能均为0.6,红方无人作战集群作战效能为0.5,侦察效能为0.6,数量比例为1.5(即无人化装备数量为600)。即x0=400,y0=1 000,Q=P1=P2=0.5,β=α1=α2=0.6,γ=1.5。如图3所示。

图3 有人/无人相对独立作战模型(红方兵力减少、无人集群增加,且有人/无人集群数量之和等于蓝方兵力)
以上三种情况说明,假设红蓝对战,其中,红方拥有无人作战集群,但兵力处于劣势;蓝方为有人作战集群,兵力处于优势。在“有人/无人相对独立作战”条件下,当红方有人/无人集群数量相同且二者之和等于蓝方兵力时,红方兵力消耗速度显著小于蓝方,红蓝方最终同归于尽;经过有人/无人集群数量比例调整后,红方在兵力增加条件下才可能取胜。由此得出以下结论。
结论一:在“有人/无人相对独立作战”条件下,红方对蓝方优势较大。在兵力相同的情况下,红方必胜;即使红方兵力处于劣势,依然有大约一半概率获胜。
结论二:在“有人/无人相对独立作战”条件下,兵力规模因子对作战的影响比无人作战集群大。
3.2 交战一方“有人/无人密切协同作战”模型
假设红蓝对战,其中,红方为有人/无人作战集群,士兵与无人化装备的侦察效能、作战效能完全一致,红方拥有无人作战集群,但兵力处于劣势;蓝方为有人作战集群,兵力处于优势。在“有人/无人密切协同作战”条件下:
1)红方兵力与无人集群数量之和等于蓝方兵力时,令红方初始兵力为500人,蓝方初始兵力为1 000人,侦察效能均为0.5,作战效能均为0.6,红方无人作战集群作战效能为0.5,侦察效能为0.6,数量比例为1(无人化装备等于士兵数量)。即x0=500,y0=1 000,Q=P1=0.5,α1=β=0.6,P2=0.5,α2=0.6,γ=1。如图4所示。
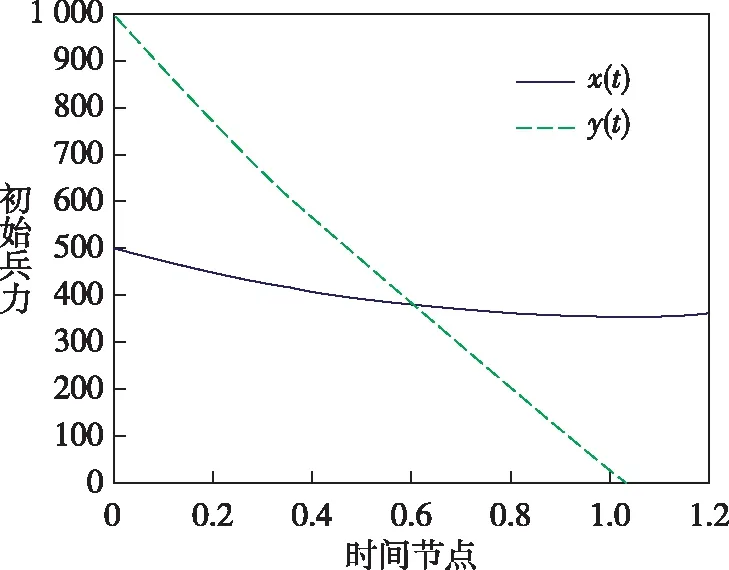
图4 有人/无人密切协同作战模型(红方有人/无人集群数量相等,且二者之和等于蓝方兵力)
2)令红方初始兵力为800人,蓝方初始兵力为1 000人,侦察效能均为0.5,作战效能均为0.6,红方无人作战集群作战效能为0.5,侦察效能为0.6,数量比例为0.25(即无人化装备数量为200);即x0=800,y0=1 000,Q=P1=P2=0.5,β=α1=α2=0.6,γ=0.25。如图5所示。
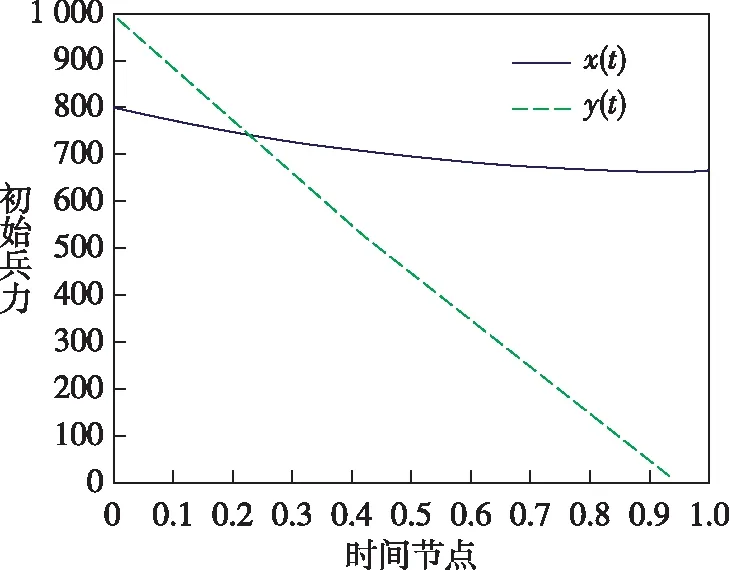
图5 有人/无人密切协同作战模型(红方兵力增加、无人集群减少,且有人/无人集群数量之和等于蓝方兵力)
3)令红方初始兵力为200人,蓝方初始兵力为1 000人,侦察效能均为0.5,作战效能均为0.6,红方无人作战集群作战效能为0.5,侦察效能为0.6,数量比例为4(即无人化装备数量为800);即x0=500,y0=1 000,Q=P1=P2=0.5,β=α1=α2=0.6,γ=4。如图6所示。

图6 有人/无人密切协同作战模型(红方兵力减少、无人集群增加,且有人/无人集群数量之和等于蓝方兵力)
以上三种情况说明,假设红蓝对战,其中,红方拥有无人作战集群,但兵力处于劣势;蓝方为有人作战集群,兵力处于优势。在“有人/无人密切协同作战”条件下,当红方有人/无人集群数量相同且二者之和等于蓝方兵力时,红方兵力消耗速度远远小于蓝方,蓝方必败;红方增加兵力,可显著加快蓝方兵力消耗速度,蓝方必败;只有当红方兵力远远小于蓝方时,蓝方才有可能获胜。由此得出以下结论。
结论一:在“有人/无人密切协同作战”条件下,红方对蓝方具有非常大的优势,即使兵力处于劣势,依然有较大概率击败对方;
结论二:在“有人/无人密切协同作战”条件下,兵力规模因子比无人作战集群对作战的影响更大。
3.3 两种协同方式对战混合模型
假设红蓝对战,双方均为有人/无人协同作战集群,且士兵与无人化装备的侦察效能、作战效能均完全一致;但红方为“有人/无人密切协同作战”,蓝方为“有人/无人相对独立作战”:
1)红方兵力与无人作战集群数量与蓝方完全一致时,令红蓝双方初始兵力均为1 000人,双方有人/无人侦察效能均为0.5,作战效能均为0.6,数量比例均为1(无人化装备等于士兵数量)。即x0=y0=1 000,Q1=Q2=P1=P2=0.5,α1=α2=β1=β2=0.6,γ=v=1。如图7所示。

图7 两种协同方式对战模型(红蓝双方有人/无人集群数量完全一致)
2)令红方初始兵力为700人,蓝方初始兵力为1 000人,双方有人/无人侦察效能均为0.5,作战效能均为0.6,红方数量比例为1.43(无人化装备数量约为1 000),蓝方数量比例为1(无人化装备数量为1 000)。即x0=400,y0=1 000,Q1=Q2=P1=P2=0.5,α1=α2=β1=β2=0.6,γ=1.43,v=1。如图8所示。
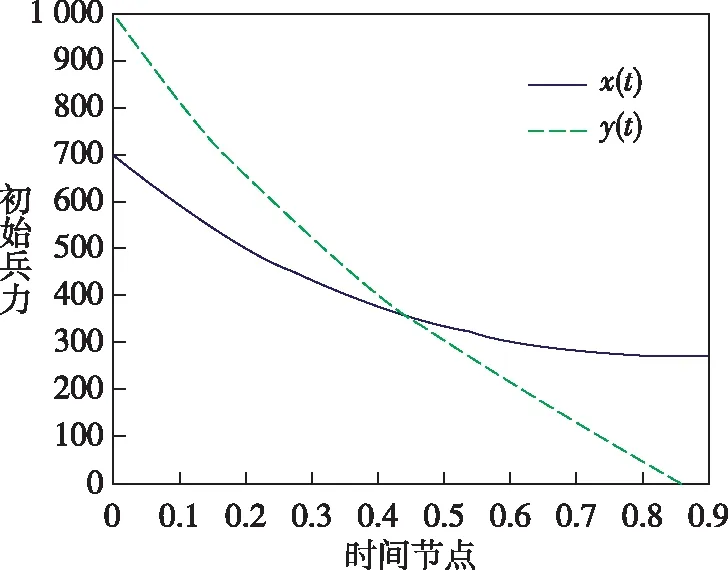
图8 两种协同方式对战模型(红方兵力较少,无人作战集群数量与蓝方相同)
3)令红方初始兵力为1 000人,蓝方初始兵力为1 000人,双方有人/无人侦察效能均为0.5,作战效能均为0.6,红方数量比例为0.1(无人化装备数量为100),蓝方数量比例为1(无人化装备数量为1 000)。即x0=1 000,y0=1 000,Q1=Q2=P1=P2=0.5,α1=α2=β1=β2=0.6,γ=0.1,v=1。如图9所示。
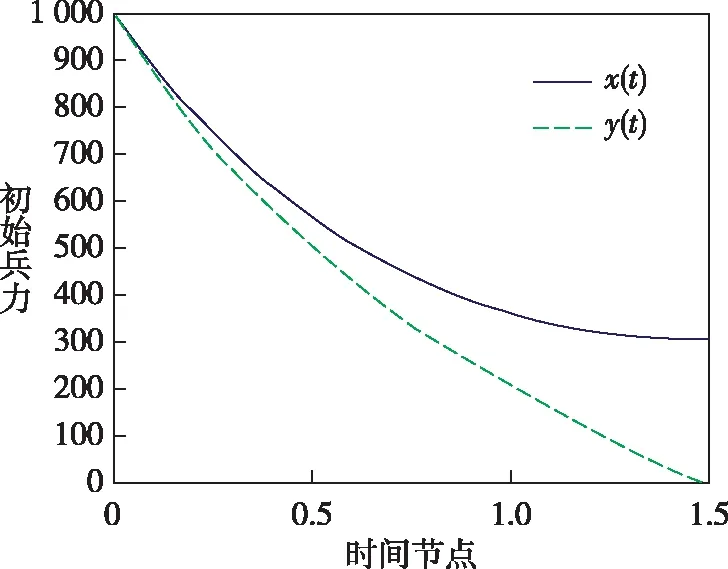
图9 两种协同方式对战模型(红方无人作战集群数量较少,兵力与蓝方相同)
4)令红方初始兵力为1 000人,蓝方初始兵力为1 000人,双方有人/无人侦察效能均为0.5,作战效能均为0.6,红方数量比例为0.5(无人化装备数量为500),蓝方数量比例为2(无人化装备数量为2 000)。即x0=1 000,y0=1 000,Q1=Q2=P1=P2=0.5,α1=α2=β1=β2=0.6,γ=0.5,v=2。如图10所示。
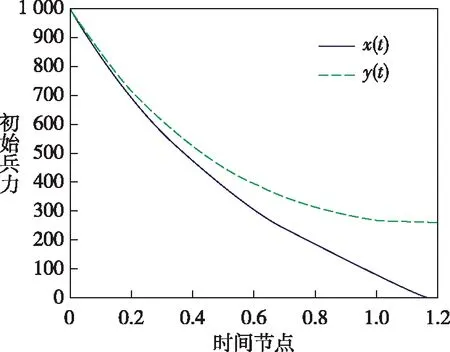
图10 两种协同方式对战模型(红蓝兵力相同,无人作战集群比例红方减至0.4、蓝方增至2)
以上四种情况说明,假设红蓝对战,双方均为有人/无人协同作战集群,且士兵与无人化装备的侦察效能、作战效能均完全一致;但红方为“有人/无人密切协同作战”,蓝方为“有人/无人相对独立作战”。当红方兵力、无人作战集群数量与蓝方完全一致时,蓝方必败;当红方兵力较少、无人作战集群数量与蓝方相同时,红方仍有一定概率获胜;当红方无人作战集群数量较少、兵力与蓝方相同时,只有在特定情况下蓝方才可能获胜(如第四种情况)。由此得出以下结论。
结论一:“有人/无人密切协同作战”相对于“有人/无人相对独立作战”,具有较大优势,红方即使兵力处于劣势,依然有一定概率击败对方;
结论二:“有人/无人密切协同作战”中,兵力规模对作战的影响远远大于无人作战集群。
4 结束语
根据现代战争中无人化装备的运用特点,本文提出了基于兰彻斯特方程的“有人/无人协同作战”模型,推导了三种情况下的数学模型表达式,并进行了仿真分析。研究结果表明:在兵力相同且其他条件一致的情况下,从整体作战效能来看,“有人/无人密切协同作战”≻“有人/无人相对独立作战”≻“传统有人作战”,且前者对后者均具有较大优势;此外,兵力仍然是“有人/无人协同作战”最重要的影响因子。这对无人化作战集群的协同运用提供了借鉴和参考,如将无人装备编配到班排级,加强“有人/无人”战术协同训练等。本文也存在一定不足:一是未区分空中无人机、地面机器人、无人自行火炮等不同无人化装备的性能特点;二是未设置打击、机动、防御、后勤等相关能力因子,不能全面反映无人作战集群优势;三是模型比较粗糙,对协同问题没有考虑协同控制层级[9]。上述问题将在下一步研究中进一步深化。

