面向模糊逻辑控制的移动群智感知多任务分配

杨桂松，张杨林，何杏宇

1(上海理工大学 光电信息与计算机工程学院，上海 200093) 2(上海理工大学 出版印刷与艺术设计学院，上海 200093)

1 引 言

随着移动设备的传感，计算和通信的快速发展，由大量携带有移动设备的参与者组成的移动群智感知成为一种新颖的感知范式[1]，并且得到极大的关注.与传统的固定部署感知模式相比，移动群智感知有部署成本低、网络维护更容易、系统更有可扩展性等优点[2],因此更适合完成大量的感知任务，例如，智能交通[3]，医疗保健应用[4]，噪声检测[5]等.近年来，也已经建立一些移动群智感知平台，如WAZE[6]，Millionagents[7]，Medusa[8]，PRISM[9].

在移动群智感知中，参与者携带的移动设备被用作基本感知单元.首先，系统平台应将任务分配给合适的参与者，然后参与者执行任务，并将感知数据上传到系统平台.最后，系统平台分析和处理感知数据以完成这些任务.其中，任务分配是一个根本而核心的问题.任务分配的研究经历了几个发展阶段.在早期的任务分配研究中，大多数研究工作集中在单任务分配[10-12].随着越来越多的应用利用移动群智感知，考虑到有限的资源(即，移动设备的数量，传感器的类型和能量等)，并且任务的数量逐渐增加，因此在有限资源下的多任务分配成为研究热点[13-15].另外，在移动群智感知中，由于参与者的感知活动受到时间和空间的影响，因此研究多任务分配的时空特性[14，16,17]具有重要意义.

在特定的时空中，参与者密度，即活动的参与者数量占所有参与者的比重，是移动群智感知的重要因素，并且对任务完成的质量和效率具有重要影响.例如，一些工作研究了参与者密度对任务分配的影响[15]和位置隐私保护[18,19].目前，获取参与者密度的一种直接方法是要求他们不停地报告实时位置，以便系统平台可以准确地查看不同区域的密度.但是，这种方法通常是不切实际的，因为它不仅昂贵，而且还会在位置隐私方面带来潜在的风险.另一种方法是与城市管理部门合作，以便系统平台可以获取参与者出行的数据.但是这种方法的灵活性较差，通常情况下，这些部门不愿意合作.因此，对于移动群智感知的应用和系统，需要另一种密度估计方法.在本文中，我们旨在解决两个挑战.1)如何准确，灵活地估算参与者密度.2)如何在参与者密度的限制条件下实现任务分配策略.

为了解决第一个挑战，我们提出了用于参与者密度分析的模糊逻辑控制方法.考虑到时空下的参与者密度是非线性且复杂的，因此难以在高参与者密度和低参与者密度之间校准清晰的边界.为了解决这个问题，在本文中，采用模糊逻辑控制方法来获取不同时间和空间下的参与者密度.作为基于规则的方法，模糊逻辑控制方法可以模拟人的思维并将专家知识转换为启发式控制算法[20].模糊逻辑控制的最重要特征是反映人们的经验和以自然语言表达的推理规则.在本文中，根据参与者的出行时间和空间来反映经验和规则，从而可以获得不同时空下的参与者密度.

另外，为了应对第二个挑战，我们提出了任务分配策略.首先，基本思想是根据参与者的密度确定任务所需的有效样本数量.例如，在低参与者密度的特定时空中，由于参与者数量不足，任务分配的效率和感知质量将降低.在这种情况下，传统的任务分配策略可能会导致较长的完成周期，甚至某些任务无法在有效时间内完成.因此，对于每个任务，根据参与者密度，如何确定其有效样本数量(合理范围内的较低值)以确保每个任务在有效时间内完成很重要.相反，在参与者密度较高的特定时空中，由于参与者数量充足，因此对于每个任务，确定其有效样本数量(合理范围内的较高值)也很重要，以便系统平台可以在有效时间内收集足够的高质量样本.另外，本文还考虑任务的属性和参与者方的因素来计算所有任务的效用.进一步地，为了最大化所有任务的效用，在参与者承载的最大工作负载和任务所需要的样本数量的限制条件下，本文提出了一种全局贪婪算法将任务分配给参与者.

总之，本文通过基于模糊逻辑的参与者密度分析，研究了多任务分配问题.本文的主要贡献如下:

1)由于不同时空下的参与者密度是非线性的、复杂的，因此采用模糊逻辑控制方法对参与者密度进行分析.

2)为了最大化所有任务的效用，提出了一种全局贪婪算法进行任务分配.

2 相关工作

一些工作研究不同情况下的多任务分配问题.Guo等人在[13]中考虑了时间敏感任务和延迟容忍任务的参与者选择问题.Song和Hu研究了如何在任务分配质量受限的情况下将多个任务分配给参与者[21,22].与这些研究工作不同，本文考虑不同时空下参与者密度的问题以进行任务分配.

在移动群智感知中，时空模型是一个热门的研究问题，近年来引起了很多关注.与典型的众包不同，基于时空模型的任务分配需要考虑任务和参与者的时空特征，例如时间，空间，时空覆盖等.例如，在文献[10]中，一种名为CrowdRecruiter的新型参与者选择框架，以通过选择少量参与者并满足时空覆盖概率约束来最小化奖励支出.Xiong等人定义了一种新颖的时空覆盖率度量，即k深度覆盖率，并在不同激励和k深度覆盖的约束下优化任务分配[16].就时间和地点而言，Cheng等人考虑每个空间任务都受时间限制，并提出了一种最优的参与者和任务分配策略，该策略可以在预算约束下最大化参与者的利益[23].

上述工作仅考虑了任务和参与者的某些时空特性，并且缺乏对参与者的时空密度进行全面分析和建模的能力.因此，就参与者密度对任务分配的影响而言，本文充分考虑了参与者密度，并采用模糊逻辑控制方法进行了分析.

作为近似推理模式的逻辑[24]，模糊逻辑已在导航系统，医疗，食品等许多领域中得到应用.在文献[25]中，开发了一种用于移动机器人的导航系统，其中，将移动机器人的传感数据用作模糊逻辑的输入，以获得不同的机器人行为.在文献[26]中，提出了一种基于模糊逻辑的专家系统，该系统可以为患者诊断可能的心脏病.文献[27]等人设计了基于模糊逻辑控制的面团发酵系统，该系统不需要数学模型，并且具有更好的抗干扰性能.

Liu等人考虑了参与者密度对任务分配的影响，他们提出了一个名为TaskMe的参与者选择框架，用于两种典型的多任务分配情况，即参与者少，任务多和参与者多，任务少，并根据这两种情况提出了不同的优化目标和算法[15].据我们所知，目前还没有其他工作将模糊逻辑控制应用于移动群智感知中的任务分配领域.因此，基于该技术，如何获得不同时空的参与者密度具有重要的研究价值.

3 效用分析

本文设计的系统模型考虑了一个实际场景，即所有任务和参与者都是双方选择.具体过程如图1所示.

图1 系统模型Fig.1 System model

首先，任务请求者将任务提交给系统平台，系统平台基于时空下的参与者密度，可以生成每个任务所需的有效样本数的样本表.然后，系统平台将任务信息(例如任务的位置，任务的感知内容以及任务的感知时间)提供给所有参与者.之后，每个参与者可以根据任务信息和自己的意愿选择任务，然后向系统平台提交意愿表.另外，系统平台通过考虑任务的感知质量，感知时间，以及参与者的感知质量，参与者的意愿性，生成所有参与者去感知每个任务的系统效用表.进一步地，系统平台基于样本表和系统效用表，通过混合贪婪算法将这些任务分配给参与者.最后，当参与者完成感知任务之后，参与者应将感知数据上传到系统平台，然后系统平台处理该数据并将结果反馈给任务请求者.

为了更清楚地表示上述过程，系统中使用的详细参数描述如下.

在这项工作中，对于某一个感知区域的时空划分，系统平台将一天划分为等长的z个时间周期TZ={T1，…，Tg，…，Tz}，并将感知区域按基站划分为l个独立的子区域SL= {S1，…，Sk，…，Sl}.在特定的时间周期和子区域中，n个任务的集合表示为tN={t1，…，ti，…，tn}，m个参与者的集合表示为pM={p1，…，pj，…，pm}.每个参与者对每个任务的意愿性用Wi，j表示，其中Wi，j= 1表示参与者pj愿意感知任务ti，否则Wi，j= 0.另外，任务ti和参与者pj的分配状态用表示，表示任务ti已分配给参与者pj，否则.应注意的是，意愿性Wi，j和分配状态φi,j均为二进制值.

在本文中，考虑到特定感知区域的时空划分，系统平台将一天划分为24个时间周期T={T1，T2，…，T24}，并将感知区域按基站划分为10个独立的子区域S={S1，S2，…，S10}，不同的子区域有不同的参与者密度.

3.1 参与者密度设计

通常，决策受到多方面不确定性的影响，决策中的信息可能是不完整，不精确，零散，不完全可靠，模糊，自相矛盾或以其他方式缺乏[27].由于模糊逻辑控制可以用计算机来执行人们的控制策略，并且避免在实际应用中建立复杂的模型，因此很多不确定性可以使用模糊逻辑来处理.由于不同时间周期和子区域中的参与者密度是非线性且复杂的，因此模糊逻辑控制方法对于参与者密度分析变得非常有益.

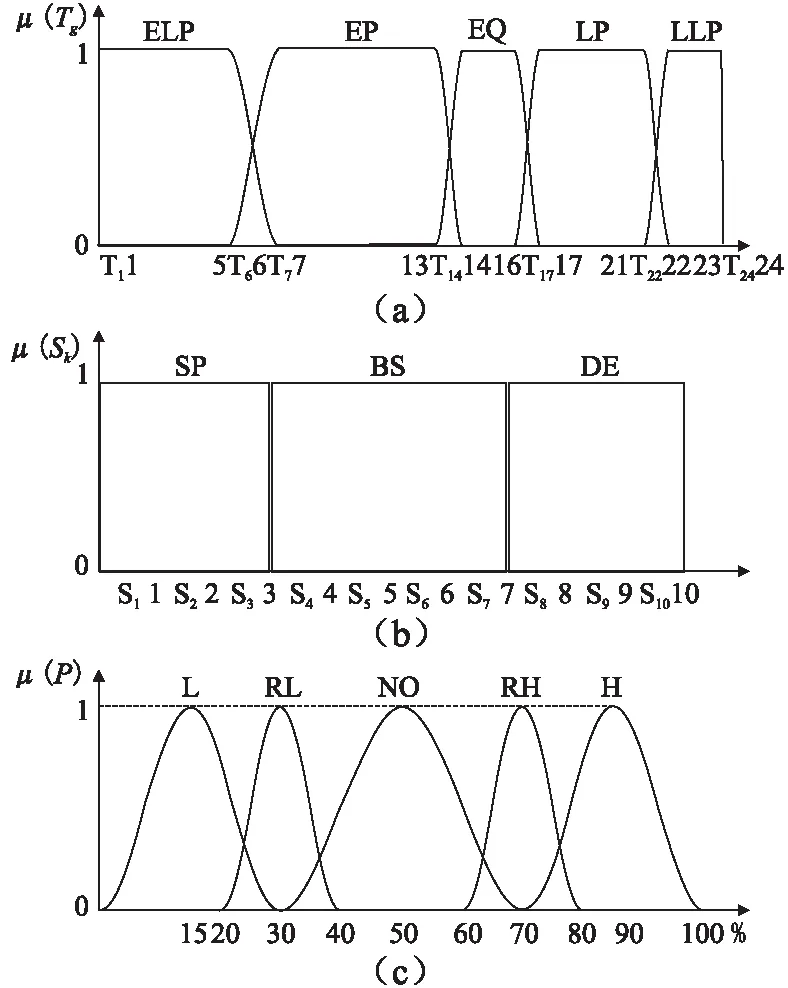
图2 隶属度函数Fig.2 Membership functions

传统的模糊逻辑控制系统以三个步骤运行，如图2所示.首先，通过隶属函数将精确的输入转换为输入变量的模糊集，即模糊化.其次，根据输出变量的隶属函数和模糊逻辑规则，系统推导输出模糊集，即模糊推理.最后，对输出模糊集进行去模糊化，将模糊值转换为系统输出的精确值，即去模糊处理.在运行模糊逻辑控制系统时，应先确定输入和输出变量.参与者密度受参与者出行的时间周期和子区域的影响.例如，在低峰期和稀疏子区域中，参与者较少，这导致参与者密度较低.相反，在高峰期和密集子区域中有较高的参与者密度.因此，在本文中，将参与者的出行时间周期Tg和参与者的出行子区域Sk作为输入变量，参与者密度P作为输出变量.

在这项工作中，详细的模糊逻辑控制系统设计如下.

模糊集和隶属度函数.使用MATLAB对模糊逻辑控制系统进行编程.在这项工作中，根据参与者的出行时间周期和子区域的经验，通过建立隶属度函数来描述输入和输出变量的模糊集.

模糊逻辑规则.模糊逻辑控制系统主要基于规则的方法来运行，该方法使用IF(条件)和THEN(结论)的可变公式化来定义规则.因此，在设置输入和输出变量之后，下一步是将它们与IF-THEN规则进行匹配，即模糊推理.在这项工作中，使用Mamdani的模糊推理方法[26]，15条规则均如下所示.另外，我们提供一个示例来说明如何评估规则.

1. IF(Tg=ELP)and(Sk=SP)，THEN(P=L).

2. IF(Tg=ELP)and(Sk=BS)，THEN(P=RL).

3. IF(Tg=ELP)and(Sk=DE)，THEN(P=NO).

4. IF(Tg=EP)and(Sk=SP)，THEN(P=NO).

5. IF(Tg=EP)and(Sk=BS)，THEN(P=RH).

6. IF(Tg=EP)and(Sk=DE)，THEN(P=H).

7. IF(Tg=BT)and(Sk=SP)，THEN(P=RL).

8. IF(Tg=BT)and(Sk=BS)，THEN(P=NO).

顶层由Sphere包围盒作为外部处理，内部加以OBB包围盒结合设计。这种设计方法主要是考虑到Sphere包围盒的构造简单性以及检测易操作两方面，如果外围的Sphere包围盒已经发生相交或者碰撞情况，则需进一步地检测，内部的OBB包围盒开始运作；如果外部Sphere包围盒还未碰撞，不进行下一步检测操作。而以OBB包围盒为内部的根节点，其中心即为Sphere包围盒的球心，进一步方便构造，而且Sphere包围盒结构方面的优势，无论被测物体进行平移还是旋转操作，其形状不发生改变，有利于更新。

9. IF(Tg=BT)and(Sk=DE)，THEN(P=RH).

10. IF(Tg=LP)and(Sk=SP)，THEN(P=NO).

11. IF(Tg=LP)and(Sk=BS)，THEN(P=RH).

12. IF(Tg=LP)and(Sk=DE)，THEN(P=H).

13. IF(Tg=LLP)and(Sk=SP)，THEN(P=L).

14. IF(Tg=LLP)and(Sk=BS)，THEN(P=RL).

15. IF(Tg=LLP)and(Sk=DE)，THEN(P=NO).

如果参与者的出行时间周期处于早期高峰，并且出行的子区域很密集，那么参与者的密度就高.可以给出表示形式，IF(Tg=EP)and(Sk=DE)，THEN(P=H).

模糊化.模糊化通过使用重心法(COG)将模糊值转换为精确值.模糊推理的最终输出值是根据隶属度函数曲线的重心和交叉坐标区域确定的[20].因此，参与者密度的精确输出值表示为.

(1)

其中Pi和Pj表示积分的第i界和第j界，而μ(P)表示隶属度函数P的值.

另外，在时间周期Tg和子区域Sk中，参与者密度的精确值是通过计算多个精确值的平均值来表示的.

3.2 效用设计

为了节省系统资源以及确保任务的感知质量，系统平台根据任务类型预先设置样本量的区间[vil,vir].实际上，一方面，如果任务ti的样本数量超过vir，则将浪费系统资源.另一方面，如果任务ti的样本数量少于vil，则无法确保ti的质量.另外，为了确保样本质量，假定每个参与者为其分配的任务提供一个有效样本.

在特定的时间周期Tg和子区域Sk中，ti所需的有效样本数量与任务ti的预区间以及参与者密度有关.任务ti所需的有效样本量和任务ti的感知质量定义如下.

定义1.假设在时间周期Tg和子区域Sk中，任务ti需要的有效样本数量定义如下：

(2)

其中，POk,g表示在时间周期Tg和子区域Sk中参与者密度的精确值.

定义2.设在时间周期Tg和子区域Sk中，任务ti的感知质量计算如下：

(3)

基于以上定义，所有任务的效用具体计算如下.

在特定的时间周期和子区域中，参与者感知任务的效用受任务的属性和参与者方因素的影响.一方面，任务的属性包括感知时间，感知质量，其中感知时间与任务的类型和复杂性有关.另一方面，参与者方的因素包括参与者的感知质量和意愿性，其中参与者的感知质量受其移动设备的性能影响.因此，对于系统平台，在时间周期Tg和子区域Sk中，参与者pj感知任务ti的效用可以计算为：

(4)

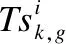
另外，在时间周期Tg和子区域Sk中，m个参与者感知任务ti的效用表示为：

(5)

因此，在时间周期Tg和子区域Sk中，所有n个任务的效用计算为：

(6)

对于系统平台，在时间周期Tg和子区域Sk中，目标是最大化所有n个任务的效用.考虑到移动设备的性能差异，一方面，每个参与者具有承载的最大工作负载fj，即可以完成的最大任务数.例如，当fj=2时，它表示参与者pj在一次任务分配中最多可以完成2个任务.另一方面，任务ti所需的有效样本数量应由不同的参与者提供.因此，以下目标函数和约束可以表示为：

(7)

约束条件：

(8)

(9)

此外，在上述问题中，我们还考虑了在时间周期和子区域中分配任务以实现最大化任务效用.

4 任务分配

在时间周期Tg和子区域Sk中，对于所有任务，将每个参与者去感知每个任务的效用建模为系统效用表，用公式(10)表示.其中，ti∈tN以及pj∈pM.

(10)

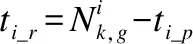
在这项工作中，使用GGA将任务分配给参与者，同时最大化所有任务的效用.此外，为了确保样本质量，参与者为每个任务只提供一个有效样本.详细的算法过程如下描述.

算法1说明GGA的执行过程.

算法1.全局贪婪算法(GGA)进行任务分配过程

2.输出： M

3.Repeat

4.forΩ≠Ødo

6.ifpj_r≠0 andti_r≠0then

7. 任务ti分配给参与者pj

8.pj_r=pj_r-1，ti_r=ti_r-1

9.elseifti_r=0then

10. Ω=Ω-ti

11.else

12. continue

13.endif

14.endfor

15.UntilΩ≠Ø or ∀pj_r≠0

16.ReturnM

图3展示了任务分配实例.在这个例子中，我们假设任务集tN={t1，t2，t3}，参与者集pM={p1，p2，p3，p4}.在任务分配之前，我们使用二分图来表示参与者去感知任务的效用，其中每条连接线代表的是参与者pj愿意去感知任务ti的效用.图3(a)展示了参与者感知任务的效用，参与者可用的工作负载以及任务需要的有效样本数的初始设置值.算法搜索系统效用表，找到满足约束条件的最大效用42，如图3(b)所示，用黑色虚线椭圆框标记42，并将t1分配给p1，同时更新t1_r=2以及p1_r=1.目前，除42外，最大的效用是38，如图3(c)所示，用黑色虚线椭圆框标记38并将t2分配给p4，同时更新t2_r=0以及p4_r=1.该算法继续搜索系统效用表，找到除已经标记过的最大效用26，此时t2_r=0，表明任务t2已经被分配完，则任务t2不会分配给参与者p3.以相同的方式进行贪婪选择过程，分别如图3(d)，图3(e)以及图3(f)所示，t1，t3，t1依次分配给p2，p4，p3.

图3 任务分配实例Fig.3 Task allocation instance

5 实验分析

为了进一步说明所提出的模型和算法的优势，我们在MATLAB和Python中对任务分配的性能进行了实验.仿真实验的主要参数在表1中给出.

表1 仿真参数Table 1 Simulation parameters

为了与提出的GGA进行比较，将其他两种算法(随机分配算法(RAA)和局部贪婪算法(LGA))作为基线，并针对在不同时间周期和子区域上的情况进行比较.

随机分配算法(RAA)-在RAA中，所有的任务都是基于随机性分配给参与者，同时要满足两个约束条件，即每个参与者承载的最大工作负载以及任务所需的有效样本数量由不同的参与者提供.

局部贪婪算法(LGA)-在LGA中，基于GGA的约束条件，所有任务将依次分配给参与者，同时通过最大化每个任务的效用来最大化所有任务的效用.

虽然本文提出的GGA在时间复杂度上面高于LGA以及RAA，但是在获得最大化所有任务的效用方面远远优于其他两个.

由于参与者密度受参与者出行的时间周期和子区域的影响，我们研究了所有任务的效用随不同时间周期和子区域下的任务数量、参与者数量以及参与者承载的最大工作负载的变化而变化.以上三种算法产生的最终仿真结果平均计算50次.

5.1 参与者密度

如第3.1节所述，参与者密度至关重要，因为它决定了系统是否可以成功分配任务.

图4显示了在不同时间周期和子区域下的参与者密度变化.在图6中，对于10个子区域S1-S10，参与者的出行时间周期设置为Tg=T20，Tg=T15，Tg=T5，即{19：00-20：00，14：00-15：00，4：00-5：00}分别隶属于模糊集LP，EQ和ELP.根据第3节中的模糊逻辑控制系统的设计，我们可以得到如图4所示的参与者密度变化，其中在时间周期T20，T15，T5时的参与者密度分别约为69%，50%和32%.显然，在时间周期T20的参与者密度高于在时间周期T15和T5的参与者密度，其原因是，在时间周期T20，有更多的参与者.总的来说，这种现象表明数值结果在实际应用中是合理的，符合模糊逻辑规则的设计精度.

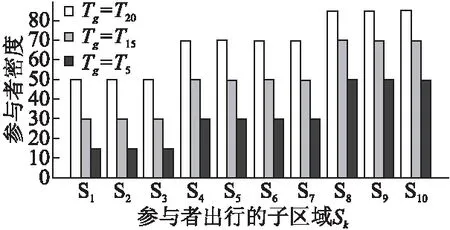
图4 参与者密度Fig.4 Participant density

根据理论分析，所有任务的效用与不同时间周期和子区域中任务的数量、参与者的数量以及参与者承载的最大工作负载有关.因此，本文分别通过使用GGA，LGA和RAA计算在不同时间周期和子区域下，不同任务数量、参与者数量以及参与者承载的最大工作负载的所有任务的效用.在仿真中，不同时间周期和子区域被设计为(a)Sk=S2,Tg=T5；(b)Sk=S8,Tg=T20.

5.2 任务的数量

在这一部分中，参与者的数量固定为50，参与者承载的最大工作负载固定为2.

如图5所示，实验结果表明，随着任务数量从5增加到25，在三种算法中，所有任务的效用均增加.另外，当最大化所有任务的效用时，GGA的性能要优于LGA和RAA.此外，当任务数量增加到一定值时，GGA，LGA和RAA生成的所有任务的效用之间的差异变得越来越明显.原因是，如第4节中所述，在每次任务分配时，GGA全局地从系统效用表里搜索最大效用以最大化所有任务的效用，而LGA是依次分配任务并且每次都是局部搜索.进一步地，随着任务数量的增加，需要将更多的任务分配给参与者，因此，GGA和LGA之间的性能差异变得更加明显.在RAA中，所有任务都是基于随机性将任务分配给参与者，因此，RAA的性能比GGA和LGA差.

值得注意的是，当任务数量增加到一定值时，所有任务的效用增加地速度变慢.这是由于，在早期过程中，参与者的数量大于任务需要的有效样本数量.进一步地，根据公式(6)，任务数量的增加将导致所有任务效用的增加.但是，随着任务数量的增加，由于可用的参与者的工作负载越来越少，算法会将过多的任务分配给有限的参与者，这将导致所有任务的效用增长速度比早期的慢.

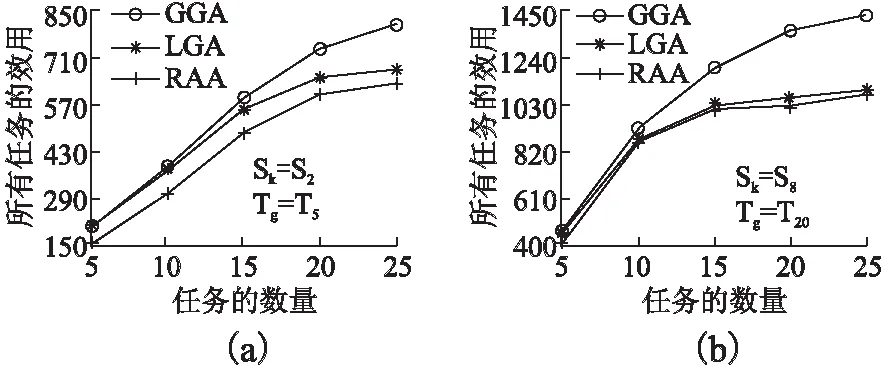
图5 不同时空下任务数量对所有任务效用的影响Fig.5 Utility of all tasks for the quantity of task in different time and space

此外，如图5(a)和图5(b)所示，在时间周期T20和子区域S8中所有任务的效用比在时间周期T5和子区域S2中所有任务的效用大.这是由于，根据第3.1节中说明的模糊逻辑规则，时间周期T20和子区域S8分别隶属于模糊集LP和模糊集DE，因此参与者密度P隶属于模糊集H.时间周期T5和子区域S2分别隶属于模糊集ELP和模糊集SP，因此参与者密度P隶属于模糊集L.因此，在时间周期T20和子区域S8，参与者密度是最大的.进一步地，根据公式(2)，任务需要的有效样本数量越大，所以需要更多地参与者去提供样本.再根据公式(5)，所有参与者去感知每个任务的效用越大，所有任务的效用越大.

5.3 参与者的数量

在仿真中，任务的数量固定为20，参与者承载的最大工作负载固定为2.

如图6所示，随着参与者数量从10增加到50，在GGA，LGA以及RAA中，所有任务的效用都增加，并且GGA的性能是远优于LGA和RAA.原因与第5.2节一样.

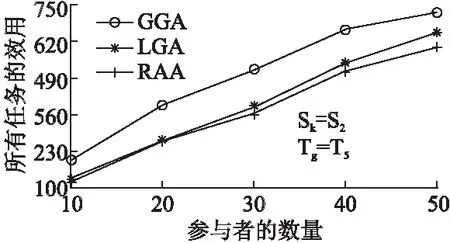
图6 参与者数量对所有任务效用的影响Fig.6 Utility of all tasks for the quantity of participant

此外，从图6还可以看出，随着参与者数量的增多，GGA的优势越来越好.这是由于，在早期分配过程中，任务的数量是大于参与者的数量，即任务需要的有效样本数是多的，因此在早期阶段，所有的任务的效用增长速度较慢.但是，随着参与者数量的增多，参与者可用的工作负载将增加，算法在资源充足的条件下，将一定的任务分配给过多的参与者，因此增长速度比早期的快.

5.4 参与者承载的最大工作负载

在仿真中，任务数量固定为10，参与者数量固定为20.

如图7所示，随着参与者承载的最大工作负载从1增加到4时，在三种算法中，所有任务的效用都是处于增加趋势，另外，可以看出GGA在最大化所有任务的效用性能上要优于LGA和RAA.原因是，GGA是通过全局的搜索最大的效用以实现所有任务的效用最大化，而LGA是局部的实现任务的效用最大化，RAA则是基于随机性进行分配任务以达到效用最大化.

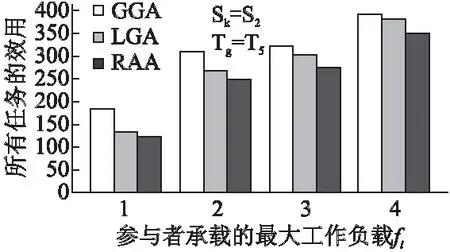
图7 参与者承载的最大工作负载对所有任务效用的影响Fig.7 Utility of all tasks for participant maximum workload

由图7所示，随着参与者承载的最大工作负载越来越多时，在GGA中，所有任务的效用越来越大.这是因为，任务的数量一定时，表明任务需要的有效样本数量一定.在早期阶段，由于参与者承载的工作负载少，因此可以被分配的任务比较少.进一步地，算法在有限的可用的工作负载条件下，将任务分配给一定的参与者，导致所有任务的效用比较低.但是随着参与者承载的工作负载越来越大时，表明参与者可以完成的任务的数量也越来越多，根据公式(5)，所有任务的效用随着可以任务数量的增加而增加.

6 总 结

在本文中，考虑到参与者密度在实际应用中的影响，我们的工作集中在通过基于模糊逻辑的时空参与者密度分析中的任务分配问题.为了解决该问题，采用了模糊逻辑控制方法来获得不同时间周期和子区域中的参与者密度.然后，基于参与者的密度和所有任务的效用，提出了一种GGA，以确保最大化所有任务的效用.仿真结果表明，该算法是有效的，并且在最大化效用方面表现良好.至于将来的工作，应更多考虑任务的复杂性、紧急性以及参与者的专业知识、时间可用性等属性对多任务分配的影响.同时，还将探索更多的优化方法.