一种高效的阻尼器优化设计方法

李 钢，翟子杰，余丁浩

(大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024)

0 引 言

阻尼器是消能减震结构的一个重要组成部分，中国现行抗震设计规范将阻尼器分为速度型和位移型2种，其中常用的速度型阻尼器有黏弹性阻尼器和黏滞阻尼器，主要利用其中黏弹性材料的剪切变形或活塞在黏滞性流体内的运动来耗散地震输入的能量；位移型阻尼器主要有摩擦阻尼器和金属阻尼器2种，前者通过摩擦片摩擦产生滞回耗能，后者通过金属材料本身的非线性变形来耗能。对于消能减震结构，阻尼器的布置及其各项参数对结构设计目标的实现具有显著影响，需通过阻尼器优化设计实现最佳的结构振动控制效果，为此，国内外学者对消能减震结构设计进行了一系列研究。Lin等[1]提出了直接基于位移的消能减震结构设计方法，并给出了各阻尼器等效线性化公式。李钢等[2]研究了直接基于位移的设计方法，提出了基于实际地震动记录位移谱的设计方法。周云等[3]针对附加位移型阻尼器的消能减震结构提出了基于性能的简化设计方法。翁大根等[4-5]分别针对黏滞阻尼器和金属阻尼器提出了实用化设计方法。

由于传统的消能减震结构设计方法依赖于工程师的设计经验，设计过程中需要对结构参数修正迭代，耗费大量时间，设计效率较低，因此随着计算机的应用和普及，大量的智能算法被引入消能减震结构优化设计中，包括拓扑优化方法、模拟退火方法、基于线性不等式的方法等[6-7]。随着遗传算法在结构优化设计中的广泛使用，国内外学者又将遗传算法引入到阻尼器优化设计中。Moreschi等[8]采用遗传算法对预期减震效果下黏滞和黏弹性阻尼器的位置和参数优化进行了研究。Ren等[9]针对形状记忆合金阻尼器，采用多目标遗传算法对阻尼器的数量和位置进行优化设计。Parcianello等[10]针对非线性黏滞阻尼器，在阻尼指数确定的情况下，采用遗传算法对阻尼系数进行了优化设计。曲激婷等[11-12]分别对速度型和位移型阻尼器提出了新的目标函数，采用遗传算法对阻尼器位置优化进行了研究。由于大多数阻尼器本身具有非线性，为简化分析，很多设计方法将阻尼器进行了等效线性化处理，但是等效线性化方法不可避免地会引入较大误差。若直接采用非线性时程分析对消能减震结构进行动力计算，则可以得到较为准确的计算结果，但是这种方法计算量大，尤其需要反复试算时，设计效率较低。Li等[13-15]提出了一种提高结构非线性分析效率的新方法——隔离非线性方法(IS-FEM)，该方法通过对材料或单元进行变形分解，建立单元的非线性变形场，并引入Woodbury公式，在非线性迭代时可避免结构整体刚度矩阵的实时更新和分解，取而代之的是对小规模的塑性矩阵进行相应运算，可显著提高非线性分析效率，尤其适用于局部非线性问题。在地震作用下，消能减震结构的非线性变形集中于阻尼器，主体结构保持弹性或者少量构件进入非线性，局部非线性特征明显，因此引入隔离非线性方法有助于提高消能减震结构的优化设计效率。在ETABS和SAP2000等软件中通常采用快速非线性分析方法(FNA)处理局部非线性问题，但是该方法只考虑连接单元的材料非线性，主体结构保持弹性[16]。事实上，在进行阻尼器优化设计时，通常难以保证主体结构始终处于弹性状态，而隔离非线性方法并未对非线性单元的位置做出要求，因此适用性更广。

本文以隔离非线性方法基本理论为基础，使用基于隔离非线性方法的纤维梁单元建立主体结构的分析模型，推导了位移型和速度型消能减震结构的隔离非线性控制方程，进一步结合基于种群可行性的约束优化遗传算法[17-19]，并改进遗传算法，使其适用于阻尼器参数优化设计，提出了一种消能减震结构中阻尼器准确、高效的优化设计方法。

1 基于隔离非线性的消能减震结构设计方法

1.1 隔离非线性基本理论

隔离非线性理论是以变形分解思想为基础发展而来的结构高效非线性算法，该方法将非线性应变分解为线弹性和非线性两部分，并引入额外的非线性自由度描述材料的非线性变形，可保持结构整体刚度矩阵不变，结构非线性行为仅通过规模较小的局部塑性矩阵进行描述，可实现非线性问题的高效计算[20]。本文以图1(uxi，uyi，uzi分别为单元第i个节点的x，y，z方向的平动位移，θxi，θyi，θzi分别为单元第i个节点的x，y，z方向转动位移，i=1，2)所示多层框架结构为例，阐述隔离非线性方法的基本思想和计算流程，该结构共有n个梁柱节点，假设每根梁柱使用1个单元进行模拟，结构总位移自由度m=6n。当对该结构进行非线性分析时，若某个线性化增量迭代步中有少量单元进入非线性(图1中的单元)，则可将其截面变形增量分解为弹性和塑性两部分，其中塑性变形场通过插值形式进行模拟，为便于有限元计算，在图1所示单元中间2个高斯积分点处设立塑性变形插值点，非线性插值点处的截面变形分解表达式为

图1 多自由度框架模型和梁柱单元

(1)

若该结构共有p个非线性自由度进入非线性状态，根据该结构此时的平衡方程及非线性插值点处的平衡条件，可得结构的隔离非线性控制方程

(2)

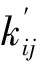
(3)

由于整体弹性刚度矩阵Ke在分析中始终保持不变，因此只需在分析开始前对其进行一次LDLT分解，在分析过程中不需要再进行相应计算。从式(3)可以看出，隔离非线性方法的主要计算量在于p×p阶Schur补矩阵的分解运算，相较于传统变刚度方法在迭代求解时对整体切线刚度矩阵(m×m阶)的反复更新与分解，隔离非线性方法可以显著提高非线性计算效率，在非线性自由度较少时，该方法的效率提升尤其明显。

1.2 附加位移型阻尼器计算方法

图2 金属阻尼器单元与双线性模型

Δq=[Δq1Δq2]T

(4)

式中：Δq1，Δq2分别为2个节点处的位移增量。

消除刚体平动位移后，其单元轴向变形增量可表示为

Δd=Δq2-Δq1

(5)

式中：Δd为单元轴向变形增量。

根据隔离非线性理论，对单元轴向变形增量进行弹塑性分解

Δd=Δd′+Δd″

(6)

式中：Δd′，Δd″分别为弹性变形和塑性变形增量。

由于该阻尼器单元为变形均匀分布的轴向单元，因此可在单元中任一点处设立塑性变形插值点，插值函数C(x)=1；弹性变形增量等于消能单元弹性刚度的逆(弹性柔度)与外力增量的乘积，即

(7)

式中：ke,d为单元弹性刚度；Δf为外力增量。

在任意线性化迭代增量步中，该单元力与变形关系还可以表示为

Δf=kt,dΔd

(8)

式中：kt,d为单元切线刚度。

将式(5)，(6)代入式(7)，可得该结构的平衡方程为

ke,d(Δq2-Δq1-Δd″)=Δf

(9)

将式(8)代入式(9)，整理并联立式(9)可得局部坐标系下金属阻尼器单元控制方程为

(10)

本文主体结构的分析模拟采用基于隔离非线性法的纤维梁单元建立，将式(10)转换到整体坐标系，并且与主体结构整体坐标系下的控制方程进行集成，可得消能减震结构的隔离非线性控制方程

(11)

(12)

cos(θy,i)cos(θz,i)]T

(13)

式中：ke,d,i中的下标i代表第i个消能单元；θx,i，θy,i，θz,i分别为该单元与x，y，z轴正方向的角度。

由于摩擦阻尼器恢复力模型与金属阻尼器类似，主要区别在于滞回曲线形状有所不同[24]，因此隔离非线性理论同样适用于摩擦阻尼器单元，摩擦阻尼器的恢复力模型可采用刚塑性模型，其摩擦起滑力对应金属阻尼器屈服力Fy，起滑位移对应金属阻尼器屈服位移uy，屈服后刚度系数为0。

1.3 附加速度型阻尼器计算方法

工程中常用的速度型阻尼器有黏滞阻尼器和黏弹性阻尼器，以黏弹性阻尼器为例，其计算模型可采用复刚度模型、Kelvin模型或Maxwell模型[24]，如图3(a)，(b)所示，恢复力曲线如图3(c)所示。假设支撑平面内刚度无穷大，其恢复力Fd可表示为

图3 黏弹性阻尼器单元与Kelvin模型

(14)

在地震作用下，消能减震结构任一增量步中的动力方程可表示为[25]

(15)

单元阻尼矩阵为

(16)

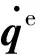
在动力计算中，黏弹性阻尼器附加的刚度矩阵始终保持不变，附加阻尼矩阵与该增量步中的速度直接相关，因此呈现非线性特征，如果每一迭代步都对整体有效刚度矩阵求逆将耗费大量的计算时间，因此结合隔离非线性基本思想将非线性阻尼项隔离，并将式(2)代入式(15)得

(17)

式(17)中符号左边各矩阵在非线性计算中均保持不变，非线性全部体现为等号右边的虚拟荷载，结合Newmark平均加速度方法对该运动方程进行处理可得

(18)

将式(19)与式(3)联立可得基于隔离非线性的结构控制方程

(19)

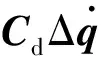
综上所述，基于隔离非线性方法求解附加黏弹性阻尼器的消能减震结构动力方程时，将黏弹性阻尼器恢复力模型中的弹性恢复力和非线性阻尼力隔离开，提高了求解效率，是一种高效的求解方法。

2 高效阻尼器参数优化设计

2.1 改进的基于种群可行性约束遗传算法

在阻尼器优化设计中，通常采用性能化设计方法，以层间位移角为约束条件，使消能减震结构在罕遇地震下满足既定的层间位移角要求。然而最优的阻尼器设计参数往往处在满足要求的最大层间位移角附近，如图4所示(θmax为计算得到的最大层间位移角，θobj为目标层间位移角)，根据各组解是否满足目标层间位移角要求可将其分为可行解与不可行解。

图4 搜索空间

从图4可以看出，个体A虽然是不可行解，但是与可行解B相比，距离全局最优解D更近，对于求得全局最优解至关重要。由于在计算前全局最优解的位置并不能确定，如果采用罚函数法直接舍弃不可行解或者降低不可行解参与交叉遗传的概率，会导致算法搜索效率较差，甚至陷入局部最优，基于种群可行性的遗传算法在每代个体中均保证一定数量的可行解与不可行解参与交叉和变异，从不同搜索方向向全局最优解逼近，是一种求解最优解位于可行域边界附近约束优化问题的有效算法。因此本文将文献[17]～[19]提出的求解该类问题的遗传算法引入消能减震优化设计领域，并作出如下改进：

(1)采用Sobol序列映射阻尼器设计变量的初始值，使得初始种群在全决策空间范围有更均匀、多样的分布[26]，适用于初始种群数量较少的情形，阻尼器优化设计中包含大量弹塑性时程分析过程，种群数量不宜过多，因此采用该方法可以充分搜索整个解空间。

(2)在选择操作中，采用基于排序的适应度分配方法，将种群按适应度值大小进行排序，再按个体在种群中的排名决定个体被选中的概率。排序后的适应度为[27]

(20)

式中：ffitness为适应度值；ppos为个体在种群中的排名；ssp为选择压力，即最优个体选中的概率与平均选中概率的比值，ssp∈[0，1]；N为个体总数。

在本小节中，我们通过具体的实验，将普通的纹理贴图、法线贴图和视差贴图三者的绘制效果进行对比来体现视差贴图的特点。

采用上述方法可以解决适应度值较大的个体使后代种群多样性急剧降低的问题。

(3)在交叉操作中，交叉产生的后代必定在两父代个体的连线上，因此本文针对可行解的内部交叉及可行解与不可行解的交叉，提出新的交叉算子，使交叉操作具有导向性

(21)

根据种群可行性对参数λ分别取值的目的是使新个体不断向可行域边界逼近，提高算法的搜索效率。

(4)在变异操作中，对可行解采用自适应的边界变异算子，即根据变异后适应度值的变化趋势自动选择变异为该基因位的最大值或最小值，使可行解向更优解方向变异；对不可行解采取高斯变异加强该算法的局部搜索能力。

2.2 高效阻尼器参数优化设计流程

本文结合改进的基于种群可行性约束遗传算法与隔离非线性方法，提出了适用于阻尼器优化设计的遗传算法GAIS-FEM，图5给出该方法的主要流程：

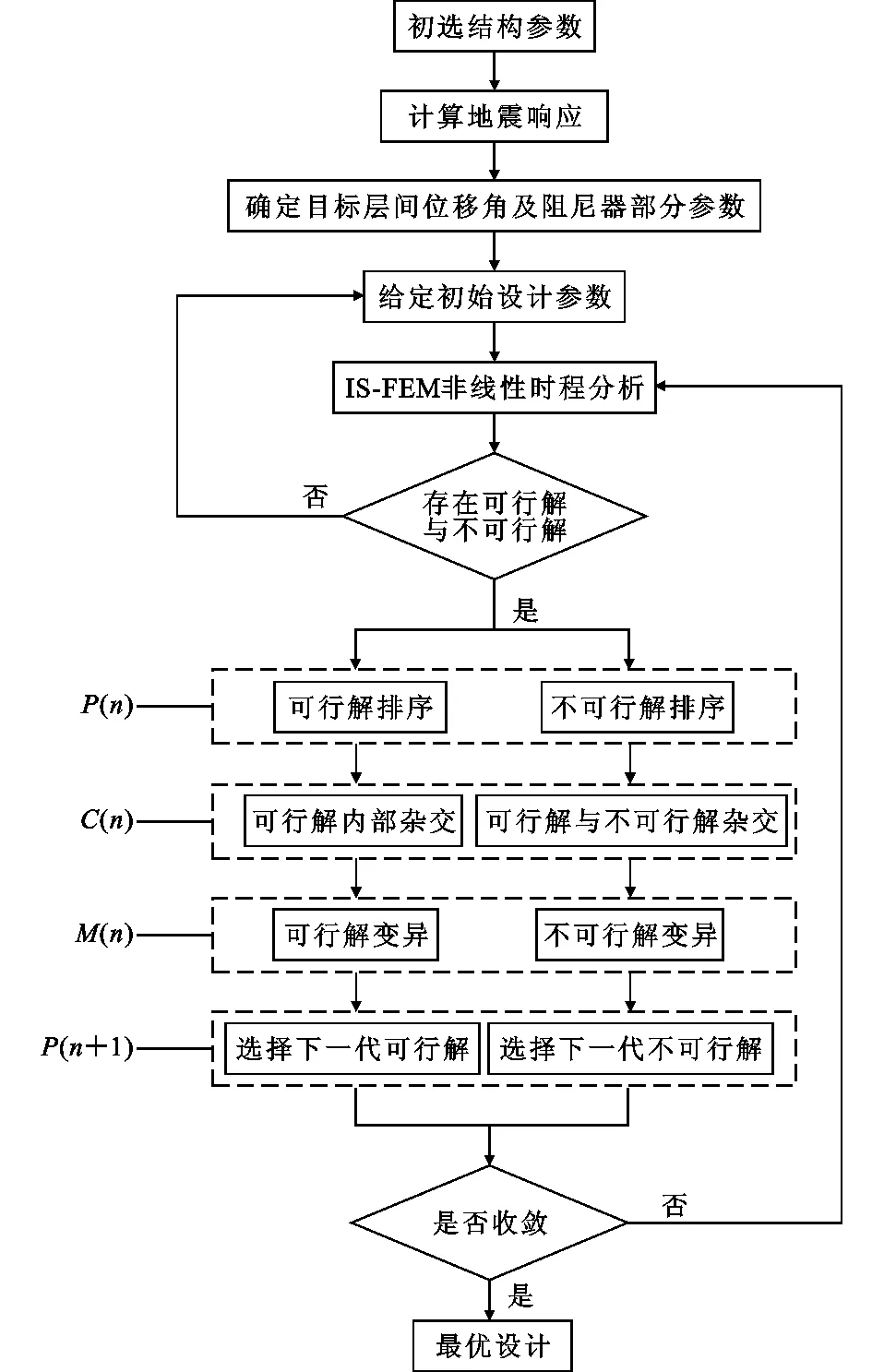
图5 GAIS-FEM流程图

(1)初选主体结构参数，计算主体结构在地震作用下的层间位移角。

(2)确定结构抗震设防目标，即消能减震结构所允许的最大层间位移角，并根据目标层间位移角预设对抗震性能影响不大或者较为固定的部分阻尼器参数值，如黏滞阻尼器的阻尼指数、金属屈服型阻尼器的屈服后刚度系数等，使遗传算法搜索区域集中在部分参数。

(3)采用MATLAB中Sobol伪随机数发生器，随机产生N组均匀分布的初始阻尼器参数，对各组参数下的消能减震结构进行IS-FEM非线性时程分析，具体分析计算流程如图6(a)所示。对比传统计算方法[图6(b)]可知，IS-FEM计算流程可避免整体刚度矩阵的重复分解计算，提高计算效率。将各组解分为可行解和不可行解，若不存在可行解或不可行解，则重新产生N组初始参数，直到两部分解空间同时存在为止。

图6 IS-FEM计算流程与传统方法对比

(4)对可行解按其目标函数值进行排序，根据式(20)计算其适应度；对不可行解按其违反度值或目标函数值排序，这样排序后选出的不可行解或者有最小的违反度值，或者有最低的目标函数值，从而提高了算法在解空间里的搜索能力。不可行解的违反度为

(22)

式中：v(θ)为违反度函数；θi为第i层的最大层间位移角。

当某个解为可行解时，v=0，否则v>0。第n代所有可行解与不可行解记为P(n)。

(5)按给定的交叉概率pc对可行解和不可行解按式(21)进行交叉。对于可行解，首先找出当前最优解，将最优解和剩下的可行解进行交叉；对于不可行解，随机选出与其数量相等的可行解进行交叉，交叉得到的新解记为C(n)。

(6)按给定的变异概率pm对可行解和不可行解采取变异操作。变异后得到的新解记为M(n)。

(7)在P(n)∪C(n)∪M(n)中采用随机遍历取样方法(SUS)选择N个下一代个体。

(8)若连续5代不再产生更优解或者达到定义的最大遗传代数，则认为该算法收敛，否则进入下一代计算。

3 数值算例

3.1 工程概况

某18层钢框架结构需要进行加固设计，该结构模型平面和立面图如图7所示，首层层高5.5 m，其余层高4 m。抗震设防烈度为8度，Ⅱ类场地，设计地震分组为第3组(特征周期Tg=0.45 s)。梁和柱分别采用H形截面和箱形截面，材料为Q235钢，构件具体尺寸见表1。楼屋面恒荷载为4.6 kPa，楼屋面活荷载为2.0 kPa。选跨中一榀框架建模分析，分析时考虑重力二阶效应，各层质量取该榀框架节点附近楼面荷载、填充墙荷载及其梁柱自质量之和，模型质量集中在梁柱节点处。

表1 结构构件尺寸

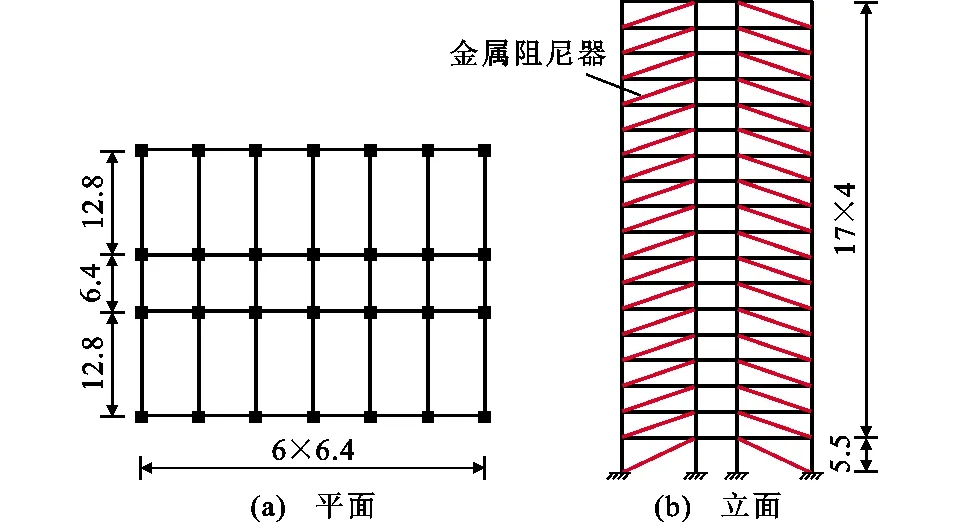
图7 18层钢框架平面和立面图(单位:m)

3.2 算例验证

为验证本文提出的基于隔离非线性的消能减震

图9 附加黏滞阻尼器(VD)的结构位移对比

结构计算方法的正确性，分别在MATLAB和ABAQUS有限元软件中建立消能减震结构进行动力计算。分别布置金属阻尼器和非线性黏滞阻尼器，金属阻尼器参数为：弹性刚度为60 kN·mm-1，屈服力为600 kN，屈服后刚度系数为0.02。黏滞阻尼器参数为：阻尼系数为400 kN·(m·s-1)-0.8，阻尼指数为0.8。主体结构采用考虑剪切变形的三维二阶Timoshenko梁单元(B32)，2种方法均采用纤维模型，其中ABAQUS中的纤维梁单元采用清华大学开发的PQ-Fiber子程序进行计算，金属阻尼器采用Axial连接单元进行模拟，黏滞阻尼器采用Dashpot阻尼单元模拟。分析中采用Rayleigh阻尼，结构阻尼比为0.02。施加调幅至400 cm·s-2的El Centro地震激励，对比2种方法的顶点位移时程曲线，如图8，9所示。2种方法计算的顶点位移时程曲线吻合较好，验证了基于隔离非线性的消能减震结构计算方法的正确性。

图8 附加金属阻尼器(MYD)的结构位移对比

3.3 设计方案及优化算法参数设置

该工程设计方案如下：采用增设金属阻尼器的措施提高结构抗震性能，设计目标为罕遇地震下结构最大层间位移角不大于1/200；目标函数为满足结构层间位移角要求所需阻尼器的最小总刚度，即

(23)

式中：f为优化目标函数；ki为第i个阻尼器的弹性刚度。

阻尼器布置方案为每层边跨设置2个金属阻尼器，每3层阻尼器参数相同，共6个设计变量；为保证阻尼器具有一定的耗能能力，各层阻尼器屈服位移均设置为6 mm。根据已有的阻尼器优化设计经验，GAIS-FEM算法中采用的参数为：初始种群数量N=30；最大遗传代数为40；交叉概率pc=0.85；变异概率pm=0.15；线性排序选择压力ssp=1.6。

3.4 地震波选取

根据《建筑抗震设计规范》(GB 50011—2010)(以下简称抗规)中第5.1.2条的相关规定[28]，本工程选取了实际2条强震记录曲线(El Centro波和Taft波)和1条人工模拟加速度时程曲线(兰州人工波)，时程反应谱(THRS)与规范反应谱(CRS)曲线见图10(g为重力加速度)，振型分解反应谱法和弹性时程分析得到的基底剪力如表2所示，符合抗规中的相关规定，因此3条波均可用于该工程设计。弹塑性时程分析中的地震波峰值加速度按照抗规8度罕遇地震的规定调整为400 cm·s-2。

表2 振型分解反应谱法和弹性时程分析的基底剪力

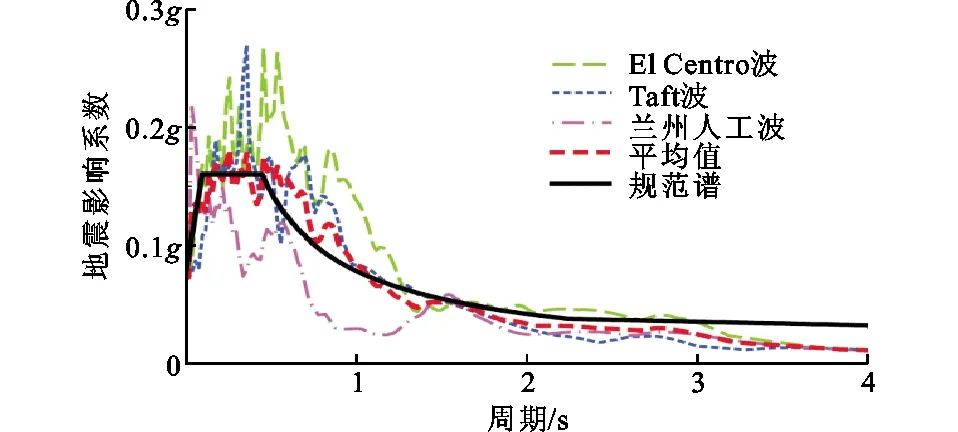
图10 时程反应谱与规范反应谱对比

3.5 优化结果分析

从每代个体的最优解变化趋势(图11)可以看出，每一代群体都在向更优解发展，并且随着遗传代数的增多，边际收益开始下降，32代以后基本保持平稳状态。图12为每代所有可行个体各基因位的方差平均值，随着遗传代数的增加，方差逐渐减小，优秀的基因(参数)被筛选和继承，因此可以认为GAIS-FEM算法计算结果较好。最终的设计结果如图13，14所示，图13为各层附加金属阻尼器的初始刚度，图14对比了无控结构和消能减震结构在3条强震作用下的最大层间位移角均值，可以发现3条地震波下消能减震结构的最大层间位移角均值从1/129.2降低到了1/201.1，成功控制在1/200的约束条件边界上，因此该金属阻尼器设计方案对结构的位移控制较为准确；由图14中原结构层间位移角可以看出，无控结构层间位移角较大的位置出现在第2，7，9，14层，对比图13的最终设计参数可以发现，这些楼层附加阻尼器的初始刚度相较于其他楼层更大，附加阻尼器后层间位移角显著减小，因此该算法可以准确地定位到薄弱层位置并加以强化，提高了整体结构的抗震能力。

图11 每代最优解变化趋势

图12 每代可行群体各基因位的方差平均值

图13 金属阻尼器的初始刚度最终设计结果

图14 无控结构和消能减震结构最大层间位移角均值

3.6 效率分析对比

算法时间复杂度理论是一种算法效率定量评价方法，其本质是算法运行所需的计算工作量，是问题规模的函数，算法的时间复杂度越低，算法的效率越高。算法时间复杂度可从运行算法的实际计算机中抽象出来，该量化结果不依赖于计算机，因此被广泛用于效率评价。李钢等[29]基于算法时间复杂度理论给出了隔离非线性方法的时间复杂度计算公式，并且对比了一个非线性迭代步内隔离非线性方法和传统变刚度法的时间复杂度大小。本文采用该文献提出如下时间复杂度公式

(24)

T2=mb2+8mb+m

(25)

式中：T1，T2分别为隔离非线性法和传统变刚度法在一个迭代步内的时间复杂度；b为整体弹性刚度矩阵的带宽；d′为非线性插值点处产生非线性的自由度数，即控制方程右下角塑性矩阵维数；α′为控制方程右上角矩阵每列最大非零元的个数；β为控制方程右下角塑性矩阵每列最大非零元的个数。

在本文算例中，结构自由度总数m=432，弹性刚度矩阵带宽b=226，与非线性自由度数目相关的参数d′，α′，β在计算中不断变化，因此具体数值不作详细说明。

在遗传算法每一代群体中，需要进行多次非线性时程分析，包含多个分析步及非线性迭代步。因此本文采用时间复杂度累加的形式，对比隔离非线性方法和传统变刚度法在GAIS-FEM中的效率，即

T1,total,i=∑T1

(26)

T2,total,i=∑T2

(27)

式中：T1,total,i，T2,total,i分别为第i代群体累加的隔离非线性法和传统变刚度法的时间复杂度。

由式(26)，(27)计算所得的每代累积的时间复杂度如图15所示，其纵坐标采用对数坐标。选取代表性遗传代数的时间复杂度大小，见表3。由表3可以看出，采用隔离非线性方法所需的时间复杂度约为传统变刚度法的1.46%，因此GAIS-FEM是一种高效的阻尼器优化设计方法。

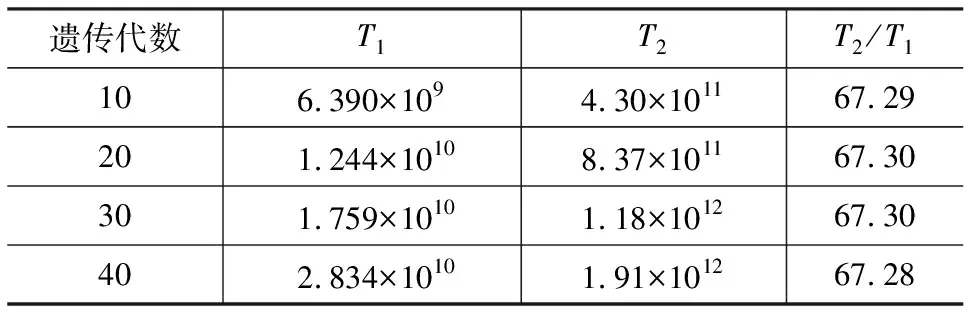
表3 2种方法时间复杂度对比

图15 隔离非线性法与变刚度法的时间复杂度

4 结 语

(1)本文基于隔离非线性理论，实现了阻尼器消能单元开发应用，拓展了隔离非线性方法的应用范围。

(2)本文改进了基于种群可行性的遗传算法，使其适用于阻尼器参数优化设计，并且提高了遗传算法在可行域边界附近的搜索能力。

(3)本文提出的基于隔离非线性的阻尼器优化设计方法通过对局部塑性矩阵的更新分解，避免了对整体刚度矩阵进行相应运算，提高了计算效率，是一种高效的阻尼器优化设计方法。