SPH方法与LBM方法在溃坝水流模拟中的对比研究

张力方，张建民

(四川大学 水力学与山区河流开发保护国家重点实验室，成都 610065)

近三十年来，新兴的基于无网格法的数值模拟方法在计算流体力学领域发展十分迅速，较为具有代表性的有光滑粒子流体动力学和格子玻尔兹曼方法。对于简单的自由面流动问题，传统的网格法数值模拟一般可以得到较为精确的计算结果，但是当自由液面发生剧烈变形时，如翻卷、破碎、液滴飞溅等现象，受限于网格尺寸等因素往往无法精确地捕捉。然而无网格粒子法在处理这些问题时能够体现其极大的优势。溃坝问题作为具有自由面大变形的经典问题之一，许多学者利用这两种方法对溃坝流进行了数值模拟来验证其可靠性。缪吉伦等[1]利用SPH方法对下游不同障碍物挑流与消能进行了初步分析。Marrone等[2]采用delta-SPH方法研究了溃坝水流冲击不同形状障碍物的自由面变形，并将预测的冲击压力与试验值和解析解进行了比较，验证了该数值方法的准确性和稳定性。叶永等[3]利用基于LBM方法研发的X Flow软件模拟了有矩形障碍物的三维溃坝问题，结果表明增强壁面函数法可以提高计算的稳定性。本文分别将SPH法和LBM法应用于模拟二维溃坝、三维溃坝水流碰撞固定障碍物，与试验值对比监测点的水深、压力随时间变化。而对于溃坝水流冲击浮体的模拟较少，尤其是LBM方法，因此两种方法还被应用于模拟浮体的位置变化，并分别与试验值对比，分析两种方法在结果上的准确性和异同点，最后对比了计算效率上的差异，得出两者的优势和不足，便于在解决实际问题时选择合适的方法。

1 研究方法

1.1 光滑粒子流体动力学

Dualsphysics[4]是基于光滑粒子流体动力学的一套开源代码，同时具有CPU并行和GPU并行，可操作性强，能够与多种算法耦合，目前发展已经较为成熟。该代码基于WCSPH模型，将流体视为弱可压缩的，控制方程为拉格朗日形式的连续性方程和动量方程：

(1)

(2)

式中：t表示时间；u表示速度矢量；ρ表示流体密度；P表示压力；g为重力加速度；υ为运动黏滞系数。

经过核函数近似和粒子近似将上式表示成SPH形式，应用delta-SPH公式[5]，在连续性方程中引入扩散项，并且在动量方程中加入人工黏性项可以消除模拟过程中产生的数值振荡，因此控制方程如下所示：

(3)

(4)

式中：ρa、Pa分别为粒子a处的密度、压强；b表示粒子a的支持域内其他粒子；rab表示粒子a和粒子b之间的距离；Wab表示光滑核函数；δΦ为可调节的无量纲参数，对于大多数模拟问题推荐取值为0.1。

光滑核函数和人工黏性项∏ab如下所示：

(5)

光滑核函数的选择对于SPH方法的模拟效果至关重要。核函数的自变量为相互作用粒子之间的无量纲距离(q)，定义为q=r/h。本文采用的三次样条函数，如下所示：

(6)

式中：αD在二维问题中取值为10/7 πh2，在三维问题中取值为1/πh3。

基于弱可压缩假定，通常使用Tait状态方程来确定压力和密度之间的关系：

(7)

边界处理方法采用动力边界条件，假定边界粒子满足与流体粒子相同的控制方程，但是不会根据作用力进行移动，而是保持固定的位置或根据自定义运动函数进行运动。当流体粒子与边界粒子之间的距离小于2倍的光滑长度，边界粒子的密度将增加，从而导致压力的增加。同时，边界粒子将对流体粒子产生排斥力，以防出现粒子穿透现象。

1.2 格子玻尔兹曼方法

X Flow软件基于格子玻尔兹曼方法(LBM)，用介观模型来模拟流体宏观行为，将水体离散模拟为微粒，研究其运动参数，具有无需网格、高效并行、边界条件处理简单等特点。LBM方法最早是由普通Boltzmann方程发展而来的。1993年，伪势模型由Shan和Chen提出[6,7]，对于采用标准的Bhatnagar-Gross-Krook (BGK)碰撞算子的伪势模型，其相应的粒子演化方程为：

fi(x+eiΔt,t+Δt)-fi(x,t)=

(8)

(9)

式中：ρ为宏观密度；u为宏观速度；αi为权重系数。

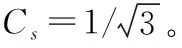
2 案例分析

2.1 二维溃坝

如图1所示，上游水体长L=1 m，高H=2 m，总计算域大小为长4 m×高3 m，求解尺度为0.01 m，计算时间为2 s。所有壁面均采用无滑移边界条件。在SPH中，水体粒子数为20 000。初始状态水体由挡板阻隔，处于静止状态，开始计算时，挡板被瞬间提起，水体在自身重力的作用下坍塌变形。

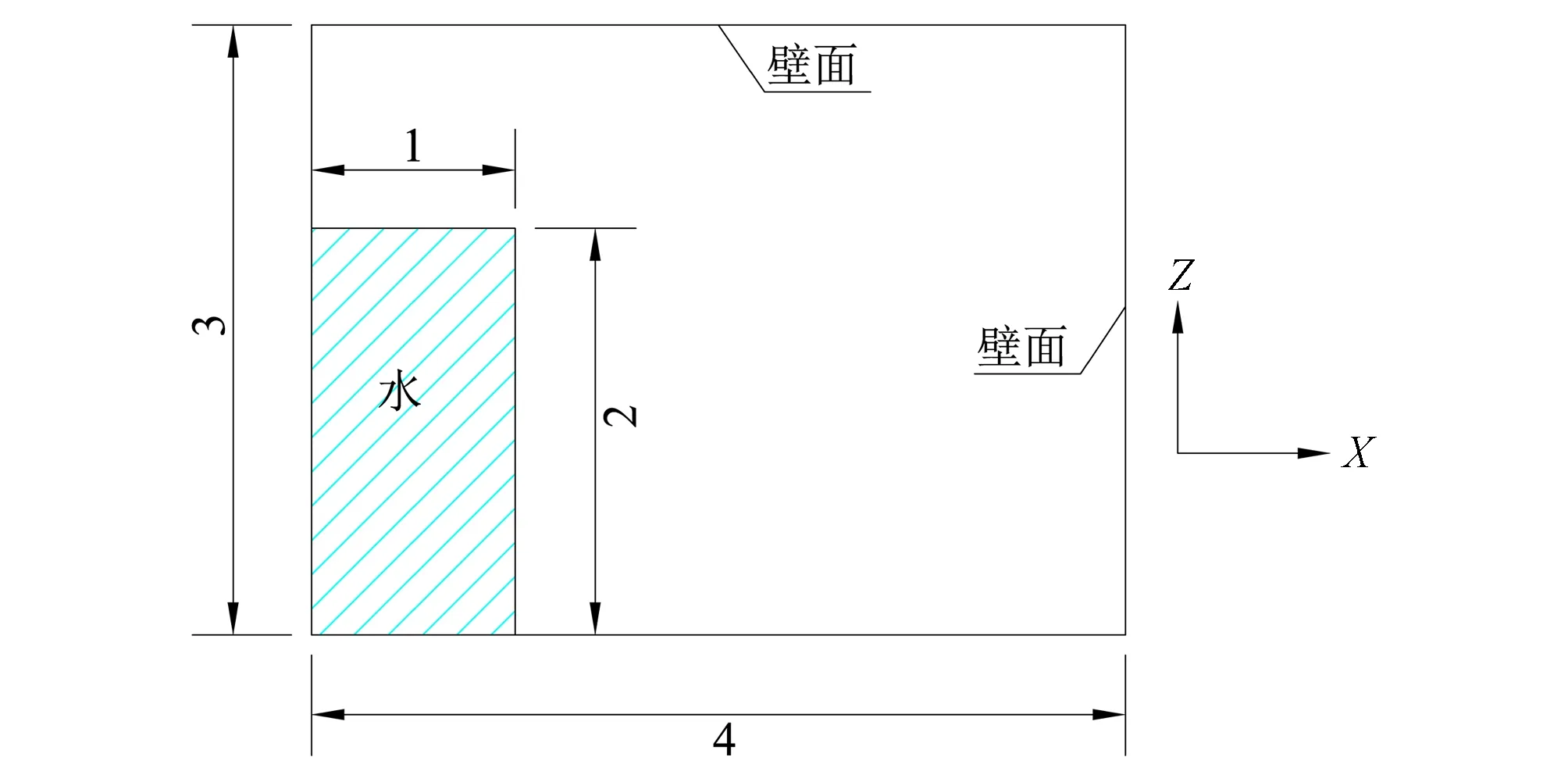
图1 二维溃坝模型立视图(单位：m)Fig.1 Elevation view of the two-dimensional dam-break model

图2展示了溃坝水流前锋位置的SPH法和LBM法的计算结果，并与Koshizuka[8]试验结果进行对比，图2中结果已进行无量纲化处理。整体上看数模结果与试验相吻合，但随着水流的行进，两者差距越来越明显，这是由于在数值模拟中未考虑底部阻力的影响，计算出的水流前缘稍快于试验结果，且SPH方法模拟结果略优于LBM方法。

图3展示了各时刻溃坝水流的自由面形状数值模拟结果，即使经历了坍塌、碰撞、翻卷、入水等过程，两种方法均能捕捉到自由面的剧烈变形情况。在t=0.5 s时刻，对于溃坝水流前缘的模拟LBM结果显得比较凌乱，而SPH结果的自由表面相对光滑，但由于SPH的固壁边界处理不够完善，在边界处产生极大的数值黏性使得粒子黏附在左侧壁面上，自由面发生滞留；在t=1 s时刻，水体碰撞墙壁向上爬升，SPH结果的水面线呈一条斜线，水体厚度随着爬升高度的增加而变薄，LBM结果的前缘粒子在爬升时逐渐破碎、分离，自由面变得不连续；在t=1.5 s时刻，中部水体由于重力原因也开始翻卷，SPH结果中前缘水体由于受到上边界和下方水体的挤压，飞溅至较远处，而LBM的前缘水体一部分沿着顶部继续滑移；在t=2 s时刻，翻卷水体与上游水面融合，两者结果均在入水时形成空腔，在剧烈碰撞后，LBM结果中部分粒子仍散落在空中。综上所述，两种方法的模拟结果与试验现象较为符合，且SPH法非常适合于处理剧烈变形的自由面问题，LBM法在自由面捕捉上仍需稍加改进。

图2 溃坝水流波前位置对比Fig.2 Comparison of wave-front position of dam-break flow

图3 各时刻下自由液面形状Fig.3 Time sequence of the free surface shape

2.2 溃坝水流碰撞固定障碍物

在实际工程中，往往由于复杂的地形特征需要考虑三维特性，在此开展了三维溃坝水体与下游方形结构物碰撞模拟，如图4所示。总计算域为3.22 m×1.0 m×1.0 m，上游水体为1.228 m×1.0 m×0.55 m。求解尺度为0.01 m，计算时间为6 s，其余设置与上述案例相同。在SPH中，水体粒子数为669 735。根据Kleefsman等人[10]在荷兰海事研究所(MARIN)进行的试验，有4个水深测点分布在水池中轴线，一个设在上游水库，另外3个设置在下游空地。在障碍物的前部和顶部上各布置4个压力传感器，如图5所示。

图4 溃坝水流碰撞固定障碍物模型布置图(单位：m)Fig.4 Sketch of the dam-break flow against fixed obstacle

图5 障碍物尺寸及压力测点布置(单位：m)Fig.5 Sketch of the obstacle and pressure measuring point

通过观察图6可知，在SPH 模拟结果中，t=1 s时刻水流与障碍物碰撞后，自由面产生剧烈变形，两侧水流绕开障碍物并向中心线运动，直至碰撞右侧墙壁，合并形成一个反向回流，与越过障碍物的水流相遇。水流沿X轴正向流速逐渐增大，在右侧墙壁中心线处流速最大达到3.7 m/s，因为这部分水流未受到阻碍，重力势能几乎全部转化为动能。

图6 在t=1 s时刻SPH方法模拟下自由面变形及速度云图Fig.6 Free surface deformation and velocity contour simulated by SPH method at t=1 s

图7展示了H1、H2、H3、H4测点处水深值时历曲线试验值与模拟值对比，数值模拟整体趋势与试验值一致。H1测点离上游最远且受障碍物阻挡，水深在约t=1 s后开始迅速增加，水流撞击右侧墙壁发生较大变形，试验与数模结果均有一定程度的波动，水流重新流向上游，水深减少，当上游水流在t=5 s时刻再次流动至H1测点，水深有所回升；H2、H3测点位于障碍物前方，水深值先后开始增加且受障碍物回流影响在短时间内陡增，约在t=4.25 s时，来自水库的回流再次撞击障碍物，水深值第二次陡增。H4测点位于上游水库，水深在t=2.5 s降至最低值0.1 m，随后受回流影响有两次陡增，一次是来自于撞击障碍物的回流，另一次是撞击最右侧墙壁的回流，说明遭遇障碍物后产生的回流会引起水深的不连续突变，不同于溃坝波的渐变式连续变化。

图7 H1、H2、H3、H4测点处水深时历曲线对比Fig.7 Comparisons of water depth time histories at H1, H2, H3 and H4

图8展示了P1、P2、P3、P5测点处压力值时历曲线试验值与模拟值对比，可以看出数值模拟较好地捕捉了障碍物受到水流冲击的压力变化过程。在t=0.5 s时刻，水流前缘碰撞障碍物前部，压力急剧上升，随后缓慢下降，在t=4.5 s时刻压力曲线出现第二个波峰，是受到反向回流冲击的影响。SPH由于采用动力边界条件，边界粒子与流体粒子之间存在一定间隔，所以测点必须放置在距离边界1.5倍光滑长度h处，在t=0.5～1.5 s时段出现明显的压力曲线波动，并且过高地估计了压力峰值，在t=1.5～4.5 s时段压力曲线比较稳定且与试验值一致，对第二个波峰的时间预测略微延迟，但压力大小较为吻合。测点P5位于障碍物顶部，约在t=1.5时刻出现压力峰值，是流体粒子碰撞后一部分翻卷落入上游，另一部分翻越障碍物砸向障碍物顶部，SPH预测值偏低，在t=4～6 s时刻，出现不合理的负压现象，一方面受制于边界处理方法的缺陷，另一方面在障碍物顶部的水深仅有0.04～0.05 m，而1.5h为0.026 m，边界处粒子数偏少，不便于压力的捕捉。LBM结果压力预测值与试验值吻合良好，无负压现象发生。综上，对于压力的处理LBM方法预测结果良好。

图8 P1、P2、P3、P5测点处压力值时历曲线对比Fig.8 Comparisons of pressure time histories at P1, P2, P3 and P5

图9 溃坝水流碰撞可运动障碍物模型平面布置图(单位：m)Fig.9 Plan view of the dam-break flow against transportable obstacle

2.3 溃坝水流碰撞可运动障碍物

Amicarelli等人[11]在巴西利卡塔大学水力学实验室进行了三维溃坝水流碰撞可运动障碍物的试验研究， 模型布置如图9所示。水槽总长3.5 m，宽0.5 m，上游水库水深为0.35 m，并在水体右侧设立闸门，其尺寸为0.037 6 m×0.5 m×0.4 m，闸门在t=2 s时开启，保持以0.11 m/s的速度向上提起。有两个固定障碍物布置在下游，分别距左边界2.5 m和2.95 m，距下边墙0.06 m和0.29 m，尺寸均为0.15 m×0.15 m×0.75 m。放置在水槽底板上的浮体为一边长为0.054 m的正方体，质量为0.073 kg，密度为464 kg/m3，其质心距离左边界2.532 m，距离上边墙0.187 m。设置粒子间距为0.01 m，SPH方法中水粒子数为86 436，强迫运动粒子数为9 800，浮体粒子数为252，浮体的动摩擦系数为0.7，恢复系数为0.6，其余边界粒子动摩擦系数为0.45，恢复系数为0.65。LBM方法中设置浮体运动方式为刚体运动，不进行任何约束，系数设置与SPH方法相同。

试验过程中，溃坝水流挟带浮体撞向第二个障碍物，由于该浮体密度小于水，被水流提升一定高度，最后移动到右岸，在下游缓慢漂浮，试验监测的浮体质心坐标变化与数值模拟结果对比如图10所示。SPH结果在t=3～4 s时差异较大，浮体起动时间较试验晚了0.5 s，说明预测的溃坝水流速度偏小，是由于DEM方法考虑了水流与底板的摩擦，之后与试验结果吻合较好。LBM方法预测的浮体起动时间与试验值一致，但是过高估计了浮体在垂直方向的位移，随水流被提升至接近0.5 m，在t=4 s时开始下落，受到右侧墙壁的反射波影响，最终漂浮到初始位置的上游，说明LBM方法对于刚体运动模拟还不够完善。

图10 可运动障碍物位置对比Fig.10 Comparison of the position of transportable obstacle

2.4 计算效率对比

数值模拟方法的计算效率也是大多数学者们较为关注的一个重要方面。本小节将对以上3个案例的计算时间进行对比，如表1所示。程序是在CPU为Intel® CoreTMi7-4790(3.6 GHz)，GPU为NVIDIA GeForce GTX 1080Ti的环境下运行的，但XFlow软件的LBM方法目前还不支持GPU并行，仅使用CPU并行进行计算。在采用相同CPU并行的条件下，LBM计算效率略高于SPH方法；采用GPU加速后，SPH 的计算速度加快了15～25倍，计算效率显著提升，说明GPU并行非常适合于粒子法，因此非常有必要实现LBM方法的GPU并行。

表1 计算时间对比 s

3 结 论

SPH和LBM方法在溃坝问题中的模拟结果与试验值大致吻合，验证了计算模型的可靠性和稳定性。对于自由液面的处理，SPH方法具有较强的自适应性使得自由面光滑、清晰，但是会出现粒子附壁现象，而LBM结果较为凌乱、破碎；对于边界处压力值的预测，LBM方法优于SPH方法，SPH法的压力值预测出现波动，是由于边界粒子积分截断导致的，需要进一步对边界条件处理方法进行改善；对于刚体运动的模拟，利用耦合DEM的SPH方法具有较好的模拟效果，LBM结果偏差较大，仍需进一步改善；在计算效率上，使用相同CPU并行的条件下，LBM计算效率高于SPH，若将GPU并行应用于拉格朗日粒子法能够极大地缩短计算时间，在计算工程问题时具有极大的应用价值。

□