基于实时监测数据的温室墒情预测研究

高国祥，王仰仁，田文艳，武朝宝，王 敏

(1.天津农学院水利工程学院，天津 300392；2.山西水利职业技术学院工程管理系，太原 030032；3.山西省中心灌溉试验站，山西 文水 032107)

0 引 言

土壤墒情[1]是影响作物生长的一个主要因素。随着气候变化的加剧和气候的不确定性，旱涝、干旱等现象频发，对农业生产的影响日益突出，带来的威胁也越来越大。根据土壤墒情监测的结果，了解土壤含水量，根据含水量的丰缺，适时采用灌水或者排水等措施。土壤墒情的监测和预报是一项重要的农业活动，对农业生产有重要的意义[2]。国内外已有许多的关于土壤墒情预报方法的研究，所采用的方法概括起来可大致分为土壤水动力学法、时间序列法、经验公式法、水量平衡法、消退指数法、神经网络模型法等[3,4]，结果表明，基于神经网络模型的训练比其他模型的训练效率更高。在相关向量机、神经网络和多元自适应回归样条的情况下，预测误差较低[5-7]。有的学者提出基于相邻时段参考作物蒸散发的土壤水分预测方法[8]，证明利用该方法预测土壤含水率也具有较高精度。

目前，我国监测土壤墒情的方法主要有人工取土法和传感器监测法两种。人工取土法精度高，但时间长，一次测量通常需要6～10 h。因此，通常每10 d进行一次监测，数据收集的频率较低。自动监测是将土壤水分传感器埋在农田土壤中，根据传感器输出的电信号与土壤水分之间的对应关系来获得土壤水分，数据采集的频率高，快速且方便[9]。

土壤墒情的变化，不仅与降水、蒸发、日照时数、风速等气象因子有关，还与土壤类型、土壤质地、土壤前期储水量、作物类型、作物所处发育期等多种因素有关，因此土壤墒情的预报是一个非常复杂的过程[10-12]。为了更加精确的预测土壤含水率，本研究根据水量平衡原理，通过实时监测土壤含水率，利用水量平衡原理以时段初的土壤含水率为自变量，采用泰勒级数对地下水补给量和蒸发蒸腾量做线性化处理，得到了以日为时段的实时墒情预测模型，由此对土壤含水率进行动态预测，为实施精准灌溉、节约农田用水提供可靠的依据。

1 材料与方法

1.1 数据来源

1.1.1 试验地概况

试验于2018年8-12月以及2019年2-9月在山西省中心灌溉试验站大棚内进行，该温室为东西走向(长47 m、宽7.5 m)，覆盖塑料薄膜，有通风系统。试验地土质为黏壤土，0～100 cm平均土壤容重1.51 g/cm3，田间持水量为26%(占干土重的%)。

1.1.2 试验设计

(1)灌水设计。设置不同水分条件处理，定期测定土壤含水量。灌溉方式为膜下滴灌。膜下铺设滴灌带，试验设2个灌水量处理，分别为D1、D2(D1为正常灌水量，D2为减半灌水量)。处理D1与处理D2之间设置宽度为1.3 m的隔离区，2年灌水处理相同。

(2)起垄覆膜方式。2018年试验地垄宽70 cm、沟宽60 cm，膜内铺设两条滴灌带，每条膜内种植两行作物，黄瓜株距50 cm、行距50 cm，茄子株距100 cm、行距50 cm，每行15株。2019年试验地垄宽55 cm、沟宽45 cm，每膜内种植两行作物，每行作物铺设一条滴灌带，黄瓜株距45 cm，行距45 cm，茄子株距60 cm、行距60 cm，每行17株。如图1所示。

(3)土壤含水率监测方式。由于传感器数量有限，考虑到种植倒茬和移动传感器影响测试精度问题，所以2018年黄瓜土壤含水率采用传感器监测，茄子土壤含水率采用人工监测；2019年茄子土壤含水率采用传感器监测，黄瓜采用传统人工监测。本研究中传感器可以按照10 cm一层间距监测土壤含水率，监测深度为1 m，每小时发送一次土壤水分监测数据。每个处理埋设两个传感器，分别在膜内两条滴灌带中间和膜外垄沟中间。人工监测每10 d一次，灌水前后加测，每20 cm一层，测试深度为100 cm。

1.2 模型构建及参数拟合

1.2.1 模型构建

水量平衡原理是指给定土体在一定的时段内，输入给土体的水量与输出土体的水量之差等于土体蓄水量的变化量[13]。大棚蔬菜的试验中，通常没有降水量，其水量平衡方程如下：

Wt+1=Wt+M-ET(θt)+K(θt)

(1)

式中：Wt+1为时段末土壤储水量，mm；Wt为时段初土壤储水量，mm；M为时段内灌水量，mm；ET(θt)为时段内耗水量，mm;K(θt)为时段内地下水补给量(或下渗量)，mm。

用土壤含水率的表达形式，可以写为式(2)：

(2)

式中：θt和θt+1分别为时段初和末的土壤体积含水率，cm3/cm3；H为土层厚度，mm。

在以日为计算时段的情况下，采用泰勒级数，把K(θt)和ET(θt)做线性化处理，即：

K(θt)=Kt+Kt+1θt,ET(θt)=at+at+1θt

整理可得：

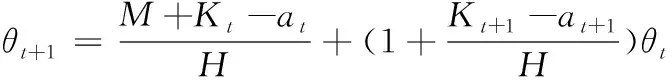
(3)

(4)

模型的内在原理为：用第t天的土壤含水率θt推求第t+1天的土壤含水率θt+1。依次可推求第3、第4、……、第n天的土壤含水率，n为预见期，本研究中设定n为5、10、15 d 3个预见期。在具有实时墒情监测数据条件下，可先由式(5)求得M，考虑建模系列长度，以日为时段，动态地进行线性回归分析，可得到逐日的模型参数a、b。

(5)

式中：Δθp为某一待定参数。

1.2.2 模型参数拟合

传感器监测数据以小时为间隔，考虑到含水率变化过程的连续性，以及为了数据分析方便，取每日12点含水率数据作为日土壤含水率监测值；考虑大棚蔬菜根系较浅，利用分层含水率值分析计算得到0～60 cm土层平均含水率，以此作为模型参数拟合依据。为了比较建模系列长度对预测精度的影响，设置了5、10、15 d 3种建模系列长度，以日为间隔，对每种建模系列长度按照式(4)做线性回归分析，可得到每种建模系列长度条件下逐日的每种模型参数a、b以及相应的确定性系数[14]DC。鉴于滴灌条件下土壤水分二维分布特性，采用膜内一点含水率的值进行了参数拟合和建模，称为模型1；采用膜内、膜外两点含水率的平均值进行参数拟合和建模，称为模型2。

1.3 模型精度评价方法

1.3.1 拟合精度分析方法

采用确定性系数(DC)分析模型的拟合精度，确定性系数的大小在一定程度上反映了预测模型的可靠程度。其值越大表示预测模型的可靠性越高，计算公式为式(6)：

(6)

式中：DC为确定性系数；y0(i)为0～60 cm土层平均含水率实时数据，cm3/cm3；yc(i)为0～60 cm土层平均含水率预测值，cm3/cm3；m为建模系列长度，本研究中设定m为5、10、15 d 3种建模系列长度。

1.3.2 预测精度分析方法

本文采用相对误差的方法对实时条件下的预测值进行预测精度分析，其方法为通过实时得到的预测值与实际测得的含水率值进行对比分析，比较两者之间的平均相对误差大小来进行预测精度分析。计算公式如下：

(7)

式中：δR为平均相对误差，%；Mi、Si分别为0～60 cm土层平均含水率的监测值和预测值，cm3/cm3；i为0～60 cm土层平均含水率的监测值和预测值的编号；N为0～60 cm土层平均含水率的监测值总数。

1.3.3 合格率分析方法

预报方案的合格率指评定中的合格点数占全部点数的百分率。其中，预报方案合格率达甲、乙等级的可用于作业预报；丙等级可用于参考性预报；丙等级以下不能用于作业预报。预测精度合格率等级评定标准见表1。合格率的计算公式为式(8)：

(8)

式中：QR为合格率，%；e为合格预报次数(合格预报次数指在准许相对误差范围内的次数)；f为预报的总次数。

表1 预测精度合格率等级评定标准Tab.1 Grade evaluation standard of qualification rate of prediction accuracy

2 结果与分析

2.1 模型参数拟合结果及分析

本研究利用传感器实时监测的土壤水分数据确定了预测模型[式(4)]参数(表2和表3)，对模型参数进行对比分析。表2和表3同时给出了模型中参数a、b的平均值和变化范围。

由表2可看出实时墒情预测模型参数的变化规律：①黄瓜正常灌水模型1的参数a随着建模系列长度的增加而增大；参

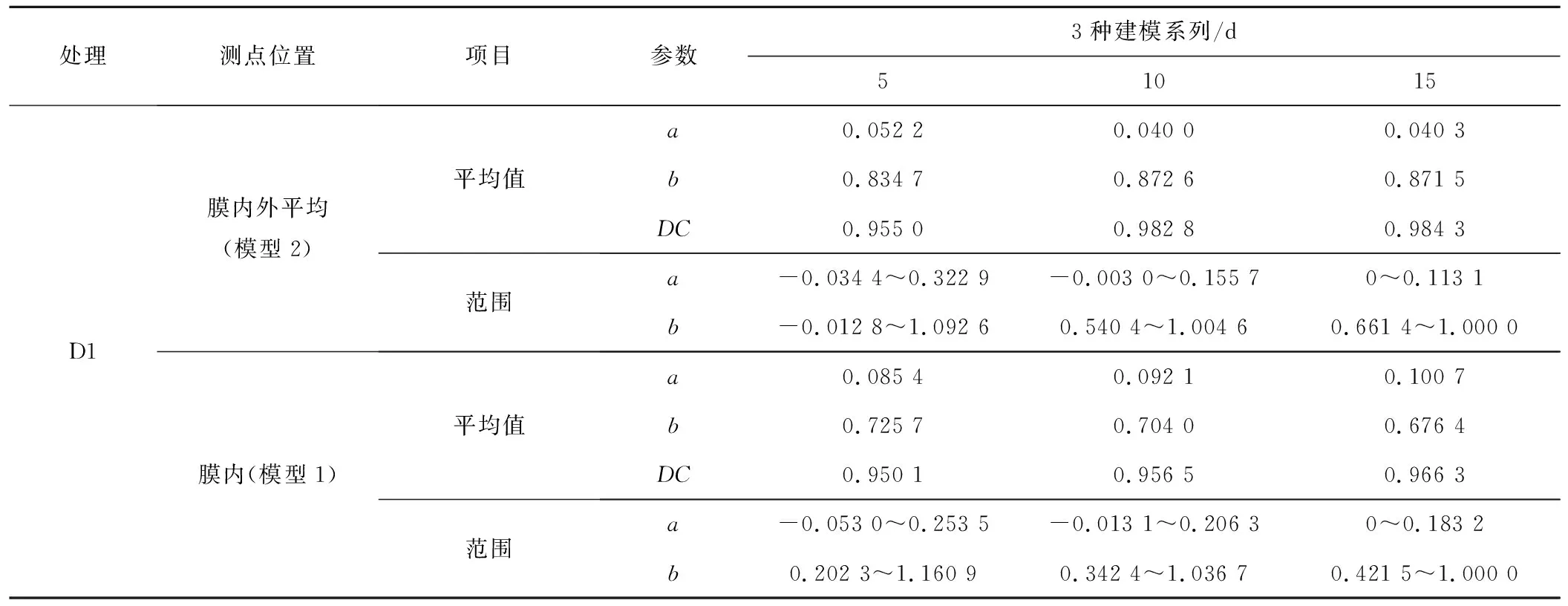
表2 2018年黄瓜不同灌水处理不同测点位置3种建模系列模型参数Tab.2 Three modeling series of model parameters for different irrigation treatments and different measurement points of cucumber in 2018

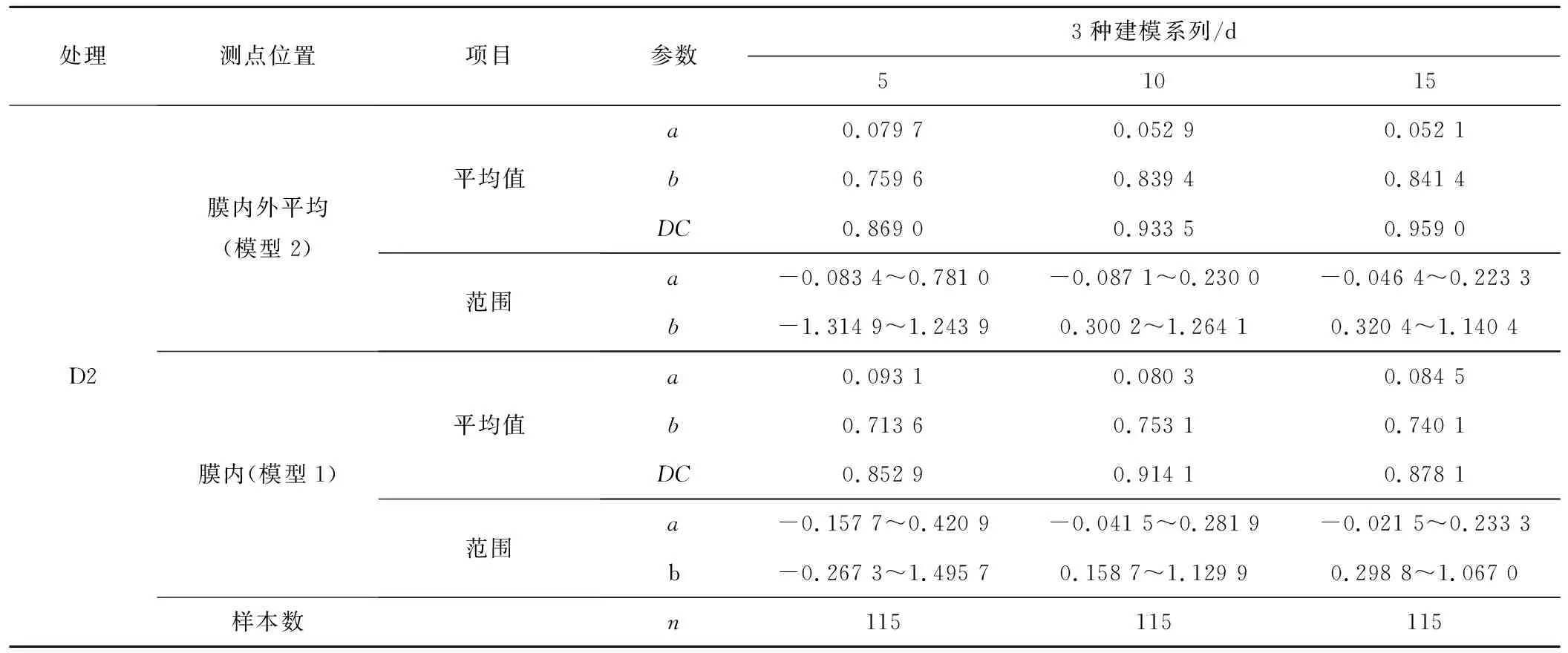
续表2 2018年黄瓜不同灌水处理不同测点位置3种建模系列模型参数

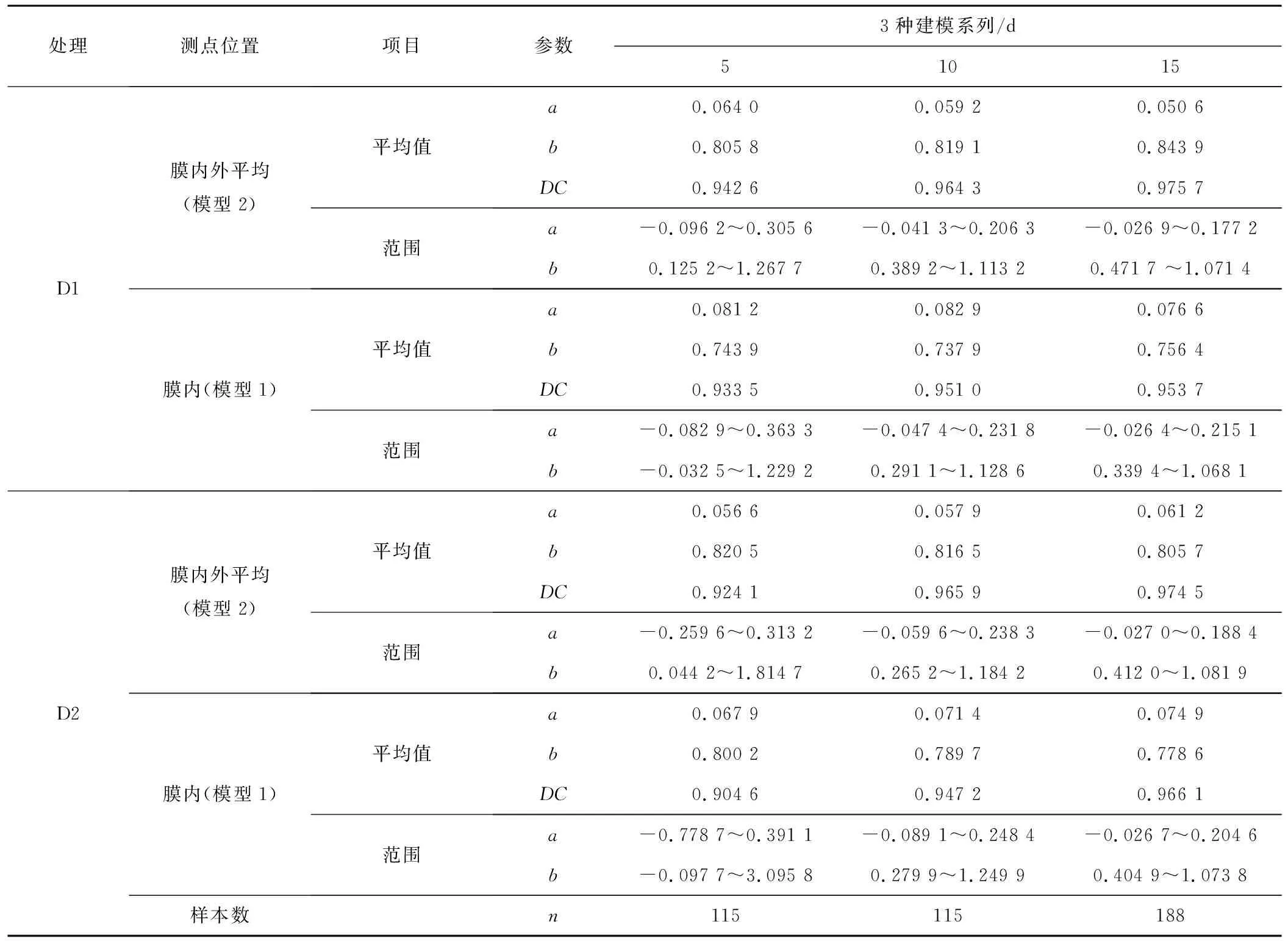
表3 2019年茄子不同灌水处理不同测点位置3种建模系列模型参数Tab.3 Three modeling series model parameters for different irrigation treatments and different measuring points of eggplant in 2019

数b与参数a的变化规律相反，参数b随着建模系列长度的增加而减小。黄瓜减半灌水模型1参数a的最大值和参数b的最小值出现在5 d建模系列， 10 d和15 d建模系列下参数a的值较为接近。②与正常灌水模型1参数a不同的是：正常灌水模型2的参数a的平均值5 d建模系列下最大；参数b在10 d建模系列下出现最大值；减半灌水模型1、2参数的变化规律和正常灌水模型1一致；③由表3也可以看出，茄子的参数a、b也具有类似的变化特性。

为了展示实时墒情预测模型参数a、b随时间的变化过程，给出了2018年黄瓜5、10、15 d 3种建模系列下的参数a、b值随时间的变化过程，见图2、图3。

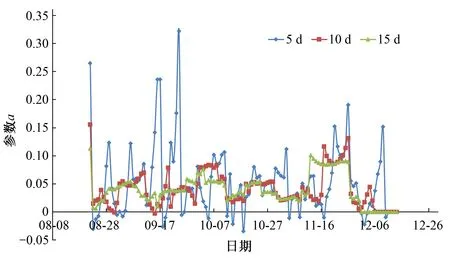
图2 2018年黄瓜膜内3种建模系列实时模型参数a随时间变化过程Fig. 2 Three modeling series of real-time model parameters a in cucumber membrane changed with time in 2018

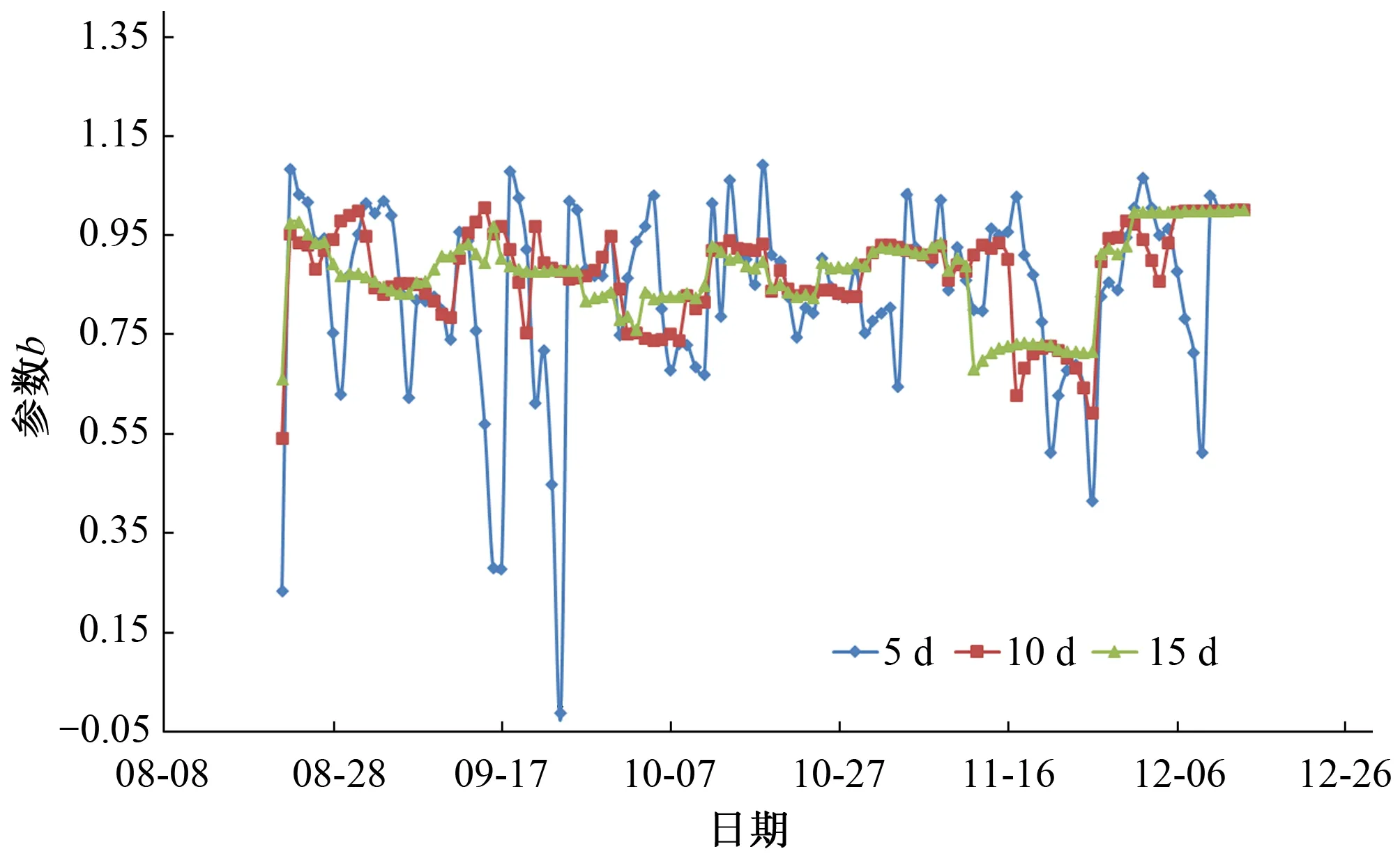
图3 2018年黄瓜膜内3种建模系列实时模型参数b随时间变化过程Fig.3 Three modeling series of real-time model parameters b in cucumber membrane changed with time in 2018

从图2中可以看出5 d建模系列的参数a随时间的变化较为剧烈，特别是黄瓜生长初始阶段，到10月7日之后幅度变得较为平缓；10 d建模系列下参数a变化幅度变得较稳定；15 d建模系列时，参数a最为稳定，变化幅度最小。从表2、表3也可看出参数a、b的变化范围随建模系列长度的增加有减小的趋势。对比图3，参数b的变化幅度随建模系列的变化与参数a具有类似的变化规律，变化幅度随建模系列长度增大而减小，参数b的变化范围具有趋于减小的趋势，与表2、表3结果一致；分析结果表明：3种建模系列的实时模型参数a、b随时间变化规律一致，参数a、b变化幅度由大到小顺序为：5 d建模系列>10 d建模系列>15 d建模系列，即在15 d建模系列下参数最为稳定。

2.2 模型拟合精度分析

2.2.1 确定性系数随时间的变化

图4为黄瓜的确定性系数随时间变化过程，可以更好地观察确定性系数DC逐日的变化。从表2可以看出黄瓜的DC值的变化表现为15 d建模系列下最大，最大为0.975 7，5 d和10 d建模系列下DC值接近。结合表3可以看出黄瓜和茄子均以15 d建模系列确定的实时墒情预测模型拟合精度最高，DC普遍较大，黄瓜达到0.87以上，茄子达到0.95以上。从图4中也可以看出与表2描述一致，建模系列长度为15 d的时候确定性系数DC较高，而5 d建模系列下DC值随时间变化幅度较大，拟合精度较低。

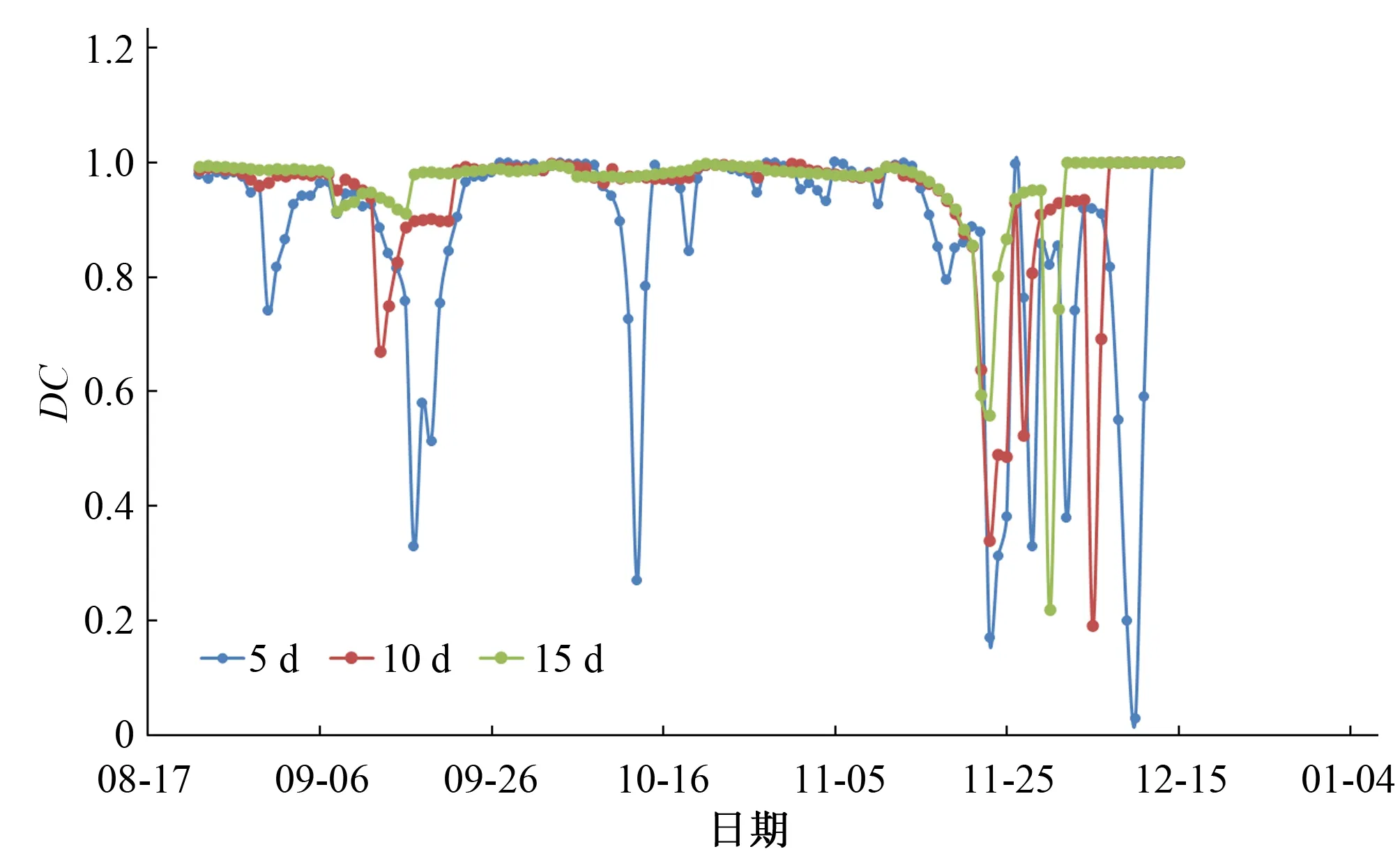
图4 2018年黄瓜膜内DC随时间的变化过程Fig.4 The change process of DC in cucumber film over time in 2018

2.2.2 参数Δθp对确定性系数的影响

以2018年黄瓜试验的处理D1为例，给出了DC与Δθp之间的关系(图4)。由图5可以看出，5、10、15 d 3种建模系列下，DC值均随着Δθp的增大而减小，当Δθp处于0.04～0.06之间时DC下降幅度最大，当Δθp增加到0.06时DC达到最小且不再变化；当Δθp为0时DC为最大值，所以本研究中取Δθp=0，可使模型拟合精度最高。

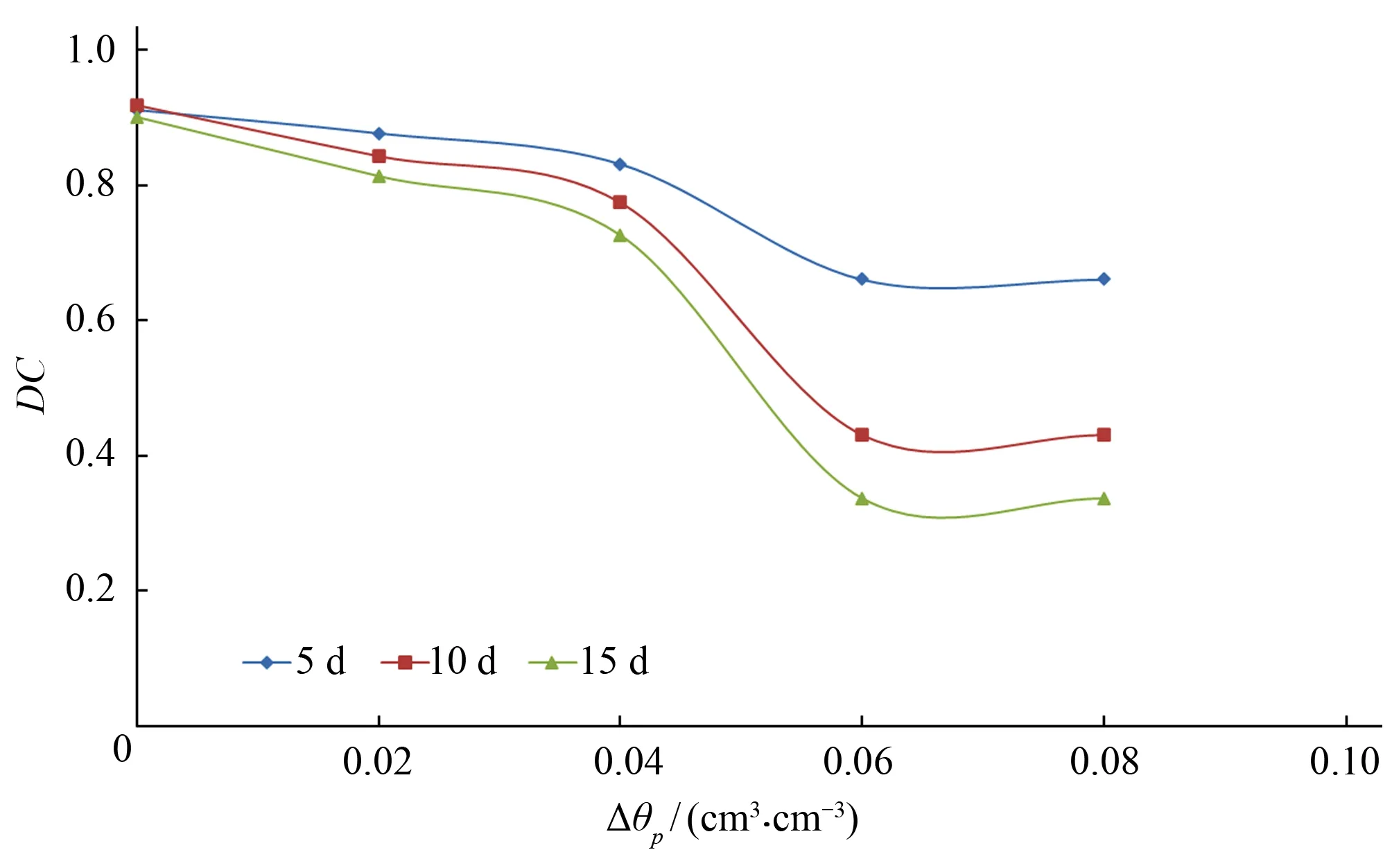
图5 2018年黄瓜膜内DC平均值随Δθp变化过程Fig.5 Change of mean value of DC in cucumber membrane with Δθp in 2018

2.3 模型预测精度分析

采用实时预测值和实测值的相对误差进行模型预测精度分析，表4给出了2018年黄瓜以及2019年茄子不同预见期的预测值相对误差平均值以及最大值。

由表4可以看出，黄瓜在相同建模系列长度条件下随着预见期增大相对误差在增大；相同预见期条件下，随着建模系列增大相对误差在减小；黄瓜处理D1的相对误差值总体大于处理D2；2018年黄瓜的预测最大相对误差在13%以内。表明该模型预测精度是比较高的。

2019年茄子墒情预测精度与2018年黄瓜有同样的变化趋势，最大误差在17%以内，略高于黄瓜的相对误差。

图6给出了2018年黄瓜平均相对误差与Δθp的关系图，可以看出3种建模系列下，实时墒情预测模型的预测值的平均相对误差随着Δθp增大而增大，同样在Δθp=0.06时最大且不再增加，Δθp=0时平均相对误差最小，同DC与Δθp之间的关系一致，Δθp对模型精度产生一定影响，Δθp=0时影响程度最低，所以模型采用Δθp=0最为合理。

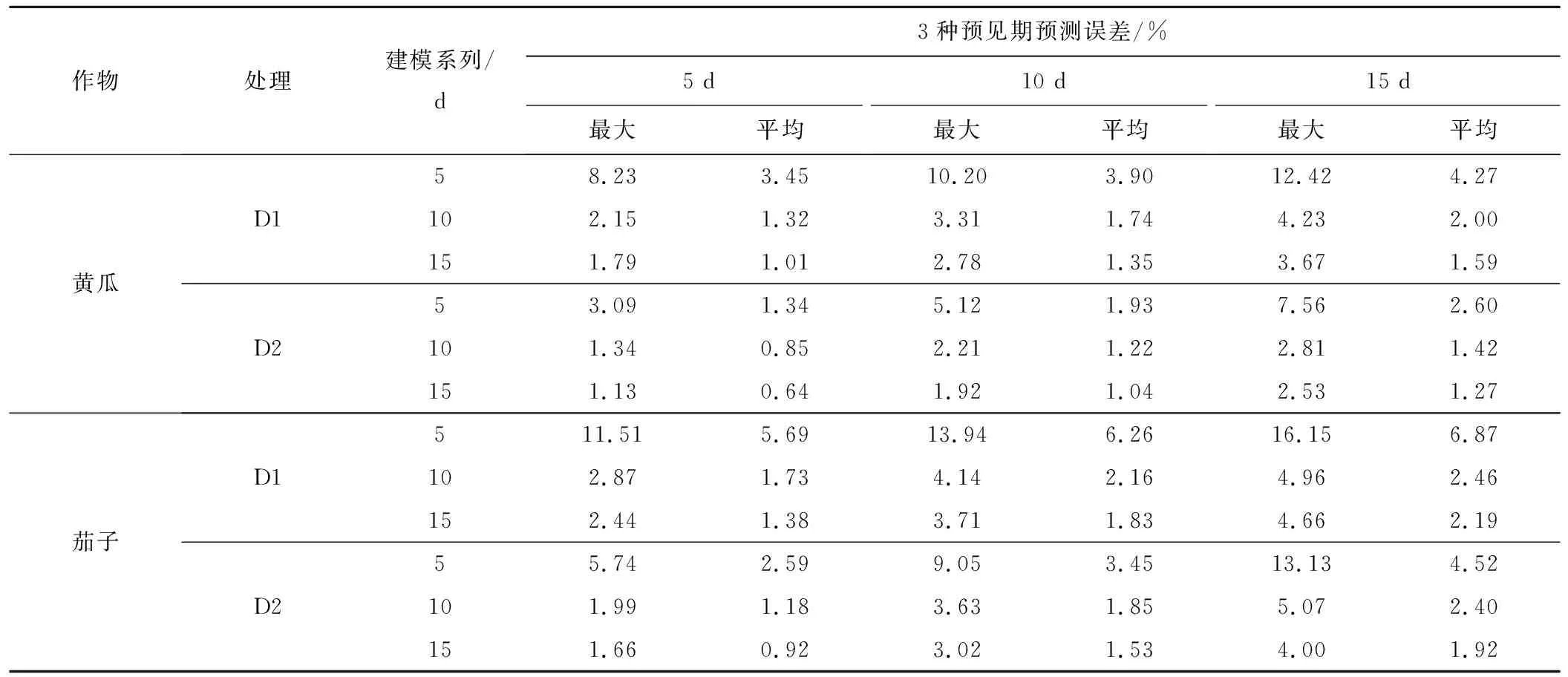
表4 3种预见期下预测值相对误差Tab.4 Mean value of relative error of predicted value under 3 prediction periods

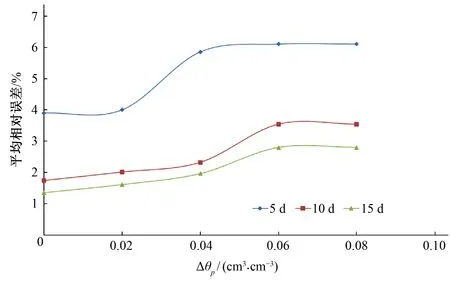
图6 2018年黄瓜膜内平均相对误差随Δθp变化过程Fig.6 Variation process of mean relative error in cucumber membrane with Δθp in 2018

2.4 合格率分析

采用式(8)计算3种准许误差值5%、10%、15%条件下的合格率，得出黄瓜、茄子不同处理墒情预测值合格率，见表5。

本文设置了5%、10%、15% 3个预测准许误差，由此评价实时墒情预测模型的预测精度。黄瓜的两个处理在3个准许误差和3个预见期下的合格率都非常高，全部为甲等，说明该模型预测的精度较高，符合预测等级要求；茄子的预测合格率也非常高，其中只有一个乙等，一个不合格，其他全部为甲等，表明本文构建的实时墒情预测模型具有较高的预测精度，达到了预测等级要求。表5合格率分析结果表明，本文提出的预测模型精度较高，同时预测模型具有实时性的特点，能够根据实时情况较为准确地预报未来5、10、15 d的土壤含水率。

表5 墒情预测值合格率 %

上述分析可见，不同作物不同处理之间模型参数a、b都是不相同的(表2、表3)，模型参数a、b随时间是动态变化的，而且变化幅度较大(图2、图3)。但模型拟合精度和预测精度均表明该模型具有足够高的精度，其主要原因是模型参数的动态变化隐含了作物生长动态变化及其实时环境对墒情预测的影响。该模型的这一动态特性确保了模型的预测精度。

3 结 论

本文基于水量平衡原理构建了实时墒情预测模型，利用实时监测的数据确定模型参数，分别对模型参数拟合结果、模型拟合精度、模型预测精度和合格率进行了分析，得出如下结论。

(1)实时墒情预测模型参数随时间的变化而变化，其变化幅度随建模系列长度增加而减小。

(2)该实时墒情预测模型对于不同作物和不同受旱程度都具有较好的适应性。

(3)随着建模系列的增大，预测相对误差在减小，15 d建模系列的预测值相对误差最小，最大误差不超过13%(黄瓜)和17%(茄子)，表明模型预测精度较高。

(4)在5%的准许误差和10 d预见期条件下，预测合格率等级均能达到乙等水平，达到了预测等级要求。