基于演化博弈的售电商组合增值服务策略

潘 悦, 魏云冰

(上海工程技术大学 电子电气工程学院, 上海 201620)

随着售电市场逐步放开以及售电市场竞争机制逐步完善,一般工商业平均电价持续下降.开放的售电市场意味着用户有自主选择权[1],用户选择售电公司的标准也不仅限于售电价格,因此售电公司仅依靠价格优势取胜变得逐渐难以实现.此时,售电公司应转变观念,以提供更为优质的售电增值服务为途径吸引更多的用户.

增值服务可分为直接增值服务和间接增值服务[2].对于增值服务的重要性国内外已有了一定的研究.Li等[3]考虑将谐波控制作为一项公共事业增值服务应用于售电策略制定.涂京等[4-6]针对用户需求响应提出售电决策方案,分别考虑对区域用户电力资源进行整合代理、建立虚拟电厂进行自适应学习等方式,从而给出更优的售电公司购售电方案.马愿谦等[7]提出针对用户电压敏感设备的“以旧换新”增值服务,将销售新设备和因服务带来的电量销售的增加作为利润,分析证明“以旧换新”服务的可行性和正确性.以上文献都只针对单一增值服务对销售策略决定的优势进行分析,并未考虑用户参与多项增值服务策略的结果,以及多项增值服务之间的相互影响.

国内外对演化博弈在售电市场的应用也有一定的研究.孙云涛等[8]提出结合层次分析法和演化博弈的用户效益分析模型,但其增值服务模型过于简略,没有明确数值标准,且未将分布式供电等合同结构作为和增值服务同等的指标.伍惠铖等[9]提出一种考虑负荷转移和多重博弈的智能小区需求响应策略,通过重复博弈得到用户最佳用电量和售电公司最优电价,但对售电公司的增值服务策略考虑不足,用户和售电公司效用模型均只考虑电价支出和收益.Raphaёl-homayoun等[10]从售电公司角度,对售电合同类型和售电时段进行分析,提出新的投资组合,但未考虑用户不同选择所带来的影响.

针对以上研究的不足,本文对负荷平移和“以旧换新”两种增值服务及其组合策略进行建模.通过Logit模型动态调整,建立多策略演化博弈模型.改变新旧设备价值的比值和“以旧换新”后的设备价格,分析组合增值服务策略的可行性.通过仿真计算得出用户对3种策略的选择情况以及不同情况下设备定价和最终售电公司的收益.

1 多策略演化博弈模型的构建

演化博弈是基于种群而非单一个体的演变,比古典博弈更适合研究群体间博弈.演化博弈强调动态平衡,在博弈中可能无法得到稳定策略,出现结果不确定的循环,或者得到多个稳定策略,比起结果的稳定,更注重于从博弈过程中得到启发,也更符合实际情况.

演化博弈放弃静态博弈的纳什均衡,引入演化稳定(ESS)概念.假设存在一个种群,它主要由采取策略i的个体和采取突变策略j的个体组成,E(i,j)表示个体选择策略i而对手选择策略j的收益,策略i为演化稳定策略,需满足的条件为E(i,i)>E(j,i)或E(i,i)=E(j,i)且E(i,j)>E(j,j).

演化博弈种群中的动态过程由演化方程来描述,常用的演化动态有复制动态[11]、扩散动态[12]和战略竞争动态[13]等.

1.1 Logit动态演化方程

Logit模型即评定模型,其中Logit在经济学上指效益.Logit模型采用Logistic概率分布函数,当策略被选择的概率Pi=Pj=0.5时,概率受目标效益影响最大,可以较好地反映概率变化.概率与效益的关系为

(1)

式中:Ui、Uj分别为选择策略i、j时的效益.

常用Logit演化方程为两策略演化博弈分析,本研究需要拓展至三策略分析,假设一个种群存在m、j和k共3种策略,选择策略j的概率为xj,此时关于策略j的演化方程为

(2)

(3)

(4)

将式(3)和式(4)代入式(2)中可得

(5)

(6)

此结果与两策略演化动态一致,开放电力市场中多组不对称演化博弈的渐近稳定性已在文献[14]中证明.

1.2 用户效益模型

博弈论模型在分析双方竞争中的收益时,由单一常量来表示,而在博弈中往往需要考虑的并不只是资金收入,还有所需承担的风险、为社会做出的贡献等.因而需要将多目标转换为单一目标,此处采用统一目标法,公式为

(7)

式中:X=(x1,x2,…,xn)为n维变量;λk为权重.结合电力市场的现有情况,将用户效益转换为4个指标:用电支付、策略选择情况、供电可靠性和增值服务.通过模型计算得出指标结果,再通过主成分分析确定各指标的权重λk.为防止数据之间由于单位不同而相差较大,导致演化博弈难以收敛,故而对各指标进行归一化处理.

2 售电用户增值服务模型的建立

2.1 负荷平移

商业用户负荷存在种类少、使用时段集中、负荷弹性水平低的特点[15],比居民用户更为可控,故本文采用商业用户进行分析.

商业用户的负荷平移主要依靠错时用电、集中负荷控制等方法.调查表明个体用户和企业对用电调整的态度为:50%不接受和50%视情况而定[16],说明参与负荷平移的用户普遍不愿意调整自己的用电习惯,此时,可推荷个体用户和企业采用蓄能类电力设备或者智能控制设备,使用户在不改变用电习惯的情况下,实现负荷平移.

对于蓄能设备,以中央空调为例,通过蓄能技术将一部分用电负荷平移至低电价时段.保证负荷平移前后制冷负荷相同,满足场地空调设备的需求.制冷负荷CL的表达式为

CL=B(Tout-Tin)+Q

(8)

式中:B为传热系数和新风比热系数之和;Tin和Tout分别为室内温度和室外温度;Q为除温度外建筑物瞬时升高的热量.

以用户满意度作为该项增值服务的评价标准,表达式为

(9)

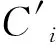
现实中负荷平移增值服务的开展会存在一些问题:一方面,在不改变用户用电习惯的前提下,需要安装新的设备,即需要资金投入,使得用户对于是否选择负荷平移产生犹豫;另一方面,如果新设备定价过低,售电公司又需要负责长时间的相关设备维护和保养,使得售电公司收益反而不如不开展此项服务.

2.2 “以旧换新”服务

“以旧换新”服务指售电公司将用户原有设备按一定价值折算入新设备售价中,从而提高用户购买欲望.电力设备有其使用寿命,当用户需要购买新设备时,售电公司在开展“以旧换新”服务的同时,可以推荐用户顾客购买蓄能类或智能类设备.

现假设某新设备i的实际价值为vi,用户对设备价值的感知系数为θi,则用户感知下新设备的价值为θivi.旧设备实际价值是新设备的βi倍(βi∈(0,1)),用户感知下旧设备的价值为βiθivi,“以旧换新”服务下新设备价格为pi,n,用户参与“以旧换新”的前提是

θivi-pi,n>βiθivi

(10)

令新设备直接购买价格为pi,d,则用户直接购买新设备的前提是

θivi-pi,d>0

(11)

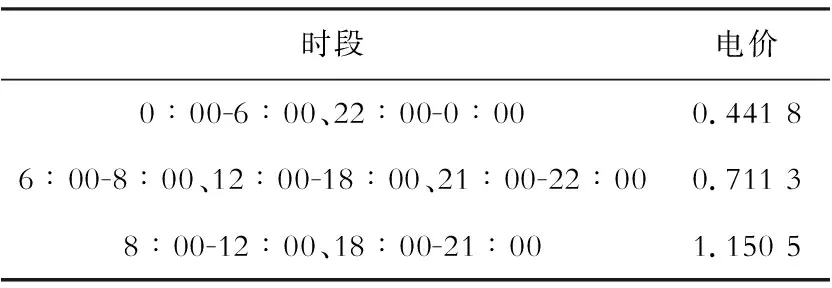
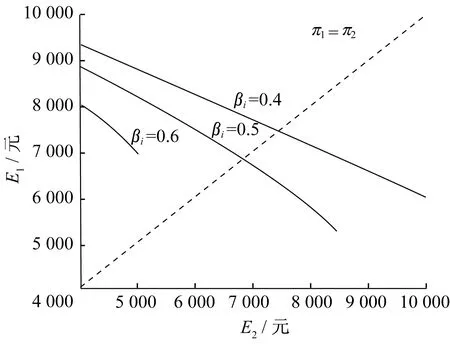
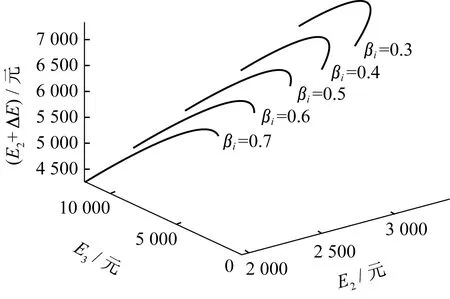
式(1)和式(2)需要满足pi,n

S2=θivi-pi,n-βiθivi

(12)

S3=θivi-pi,d

(13)

参与“以旧换新”和负荷平移时售电公司的收益E2和E3分别为

E2=Ei+Ei,n-Ei,m

(14)

E3=Ei+Ei,d-Ei,m

(15)

式中:Ei为原先售电产生的利润;Ei,n和Ei,d为销售设备产生的利润;Ei,m为设备维护费用.

新设备成本为ci,则

Ei,n=pi,n-ci

(16)

Ei,d=pi,d-ci

(17)

假设存在用户对待增值服务态度的4种场景,不同场景下用户的满意度和支付以及售电公司的收益见表1.

表1 4种场景下用户和售电公司模型Table 1 Models of users and electricity suppliers companies under four scenarios

对于用户,支付主要由用电支付和设备支付两部分组成.不参与负荷平移时用电支付为C1,参与负荷平移后为C2.普通新设备支付为p1·d,负荷平移相关新设备支付为p2·d.当不参与增值服务时,满意度为0;参与负荷平移的满意度为购买设备的满意度与负荷平移部分满意度之和.对于售电公司,当用户两项服务均参加时,公司总收益为“以旧换新”部分获得的收益与负荷平移后带来电量增加的收益(ΔE).

3 算例分析

假设售电公司开展“以旧换新”服务,设备的价值、成本和价格感知系数参考文献[7],标幺值为[v1,v2,c1,c2,θ1,θ2]=[7,8,1.5,2.1,0.7323,0.8612].该公司采用分时电价,其分时电价见表2.

表2 某售电公司分时电价Table 2 Time-of-use electricity price of a power sale company 元/(kW·h)

某区域用户负荷平移前后的单日负荷如图1所示.

图1 负荷平移前后单日负荷曲线Fig.1 Daily load curve before and after load shift

分别将“以旧换新”和组合策略,与用户不参与增值服务的情况进行比较,通过改变新旧设备价值比值βi和“以旧换新”新设备定价pi·n,反应售电公司收益的变化,结果如图2和图3所示.直线π1=π2表示两策略收益相等,当曲线在直线下方时,即新服务的收益高于原策略.为便于研究,将两策略收益限制在[4 000,10 000]之间.

图2 “以旧换新”和无增值服务收益比较Fig.2 Revenue comparison of “trade-in” and non-value-added services

图3 组合增值服务和无增值服务收益比较Fig.3 Revenue comparison of combined value-added services and non-value-added services

观察图2,随着βi的上升,用户对“以旧换新”的参与度逐渐降低,当βi超过一定数值后,即当用户的设备更换年限尚短时,用户不会考虑参与“以旧换新”服务,其收益自然低于原策略.当βi增大时,随着pi,n减小,曲线下降加快但也会变短,表示即使设备较新,但售电公司仍可以依靠低价新设备吸引用户,但是会受新设备成本所限.

同时,随着pi,n下降,“以旧换新”带来的收益越高,当定价高于定值时,曲线在直线π1=π2上方,即“以旧换新”新设备定价较低时才能受到用户青睐,与实际情况相符.

比较图2和图3可以发现,βi范围有所扩大.经过计算,“以旧换新”时βi≤0.57,组合策略时扩展到βi≤0.73,增加了用户参与增值服务的可能性,组合策略可以弥补“以旧换新”的不足.曲线与直线π1=π2交点的结果对比见表3,可以发现组合策略在收益较低的情况下即可优于原策略,相应时刻的用户选择概率也将高于“以旧换新”,即使“以旧换新”新设备的定价提高也可以获得足够多的用户支持.这表明,组合策略更易被用户接受,“以旧换新”新设备定价空间也有所提升,并且解决了部分用户因不愿意购买新设备而不参加负荷平移的问题.

表3 “以旧换新”和组合策略对比Table 3 Comparison of “trade-in” and combination strategy

固定负荷平移新设备售价标幺值p2,d=5,售电公司开展“以旧换新”、负荷平移和组合策略3种策略演化博弈下收益对比如图4所示.可以明显发现负荷平移时售电收益上界最高,这是因为其除了售电收益外,还有直接售出新设备的收益.

图4 3种策略收益比较Fig.4 Revenue comparison of three strategies

观察曲线在x轴和z轴上的投影,可以发现随着βi减小,“以旧换新”和组合策略的收益逐渐提升,符合之前的结论.且随着p2,n减小,收益曲线出现明显的拐点,由于售电公司需要维护设备,定价过低会减少收入.随着βi减小,拐点处的p2,n增大,当βi=0.3时,p2,n,l=3.5.

p2,d=5时改变p2,n,3种策略演化博弈用户选择情况和售电公司总收益变化曲线如图5所示.

由于只有一家售电公司,所以随着p2,n增大,用户有多种策略可供选择,售电公司收益持续增大,但有减缓的趋势.同时由于p2,n增大,用户会更倾向于直接购买新设备,此时“以旧换新”和组合策略选择人数都会下降.当βi=0.3时,组合策略和负荷平移选择情况会出现交点,而随着βi增大,相对负荷平移和组合策略将不存在优势,但仍有超过三分之一的用户会选择组合策略.

由于不同用户旧设备的实际情况各有不同,未必都会选择组合增值服务.所以对于售电公司而言,不能用组合增值服务代替单一增值服务,而是将组合增值服务作为一种服务套餐,供用户按照各自需求进行选择.并且随着“以旧换新”设备定价增大,组合增值服务对用户的吸引力逐渐下降,单一售电公司的收益增长也会逐步放缓.由于我国现有售电市场为竞争性售电市场,可以预见此时售电公司将流失部分用户.

由此可见,如何更好地确定新设备定价p2,d和“以旧换新”设备定价p2,n,对于售电公司而言尤为重要.售电公司收益拐点处p2,d和p2,n的值见表4,分析可知设备定价比值适宜范围在0.667～0.725之间.

表4 新设备定价和“以旧换新”定价Table 4 Pricing of new equipment and “trade-in”

4 结 语

本文将Logit动态演化博弈应用于用户多策略选择模型中,对用户策略选择情况进行分析.研究可知,组合增值服务策略可以弥补单一增值服务的缺陷.相较于“以旧换新”,组合增值服务的优势有:1) 吸引用户及时更换设备,扩大增值服务受益群体;2) 售出价格较高的新设备,增加出售设备所获利润;3) 通过负荷平移减少用户支出,增大用户接受程度.同时,组合增值服务通过使用智能控电设备和减少用户用电支出解决了现阶段个体户和企业家用电调整接受程度较低的问题.

本文还通过试验数据仿真对设备定价提出建议,得出“以旧换新”设备定价约为新设备定价的2/3时,售电公司可获得最大收益.