基于组合相关函数的AltBOC（15，10）信号的无模糊跟踪方法

袁志鑫，周艳玲

（湖北大学计算机与信息工程学院，武汉 430062）

（*通信作者电子邮箱sunnyzhou@hubu.edu.cn）

0 引言

在全球导航卫星系统（Global Navigation Satellite System，GNSS）中，交替二进制偏移载波（Alternate Binary Offset Carrier，AltBOC）调制信号具有显著的优势，欧洲伽利略系统在E5 频带（1 164 MHz～1 219 MHz）中采用了此信号［1-3］。在Galileo E5 中，下边带被命名为E5a，而上边带被命名为E5b，中心频率分别是1 176.45 MHz 和1 207.14 MHz。AltBOC 信号是双频恒包络调制信号，该信号可以将位于E5a 和E5b 上的两个四相移键控信号合并为恒定的包络信号，所以AltBOC调制能够在上下频带上承载不同的服务，这两个子频带可以独立接收和处理以实现与传统二进制相移键控（Binary Phase Shift Keying，BPSK）信号相同的性能［4］；并且恒定包络的AltBOC 信号可以降低实现复杂度并减少传播时间的不稳定性［5］。

对于接收机，采用多路复用传输的E5a 和E5b 信号允许三种可选接收机来实现和处理［6］。因此，与传统的二进制相移键控信号相比，AltBOC 信号可以提供更好的码跟踪精度并获得更好的定位精度［4］。但是，AltBOC 信号存在严重的跟踪模糊问题。由于AltBOC 调制信号的子载波为其自相关函数（AutoCorrelation Function，ACF）带来了多个正负峰值，接收机可能会误锁在其中一个副峰，这将导致现代导航无法容忍的偏差测量［7-8］。因此，需要更好的方案来解决模糊问题。

为了减轻或者消除AltBOC 调制信号跟踪过程中的模糊问题，国内外相关文献已研究出了几种典型方法：1）类二进制相移键控（BPSK Like）法通过实现一对可以单独使用，也可以非相干组合使用的信号单边带相关接收机来消除副载波调制的影响［6］。因此，每个旁瓣被独立地视为BPSK（10）信号，它提供了具有较宽峰值的无模糊相关函数；但是BPSK Like 方法会在消除模糊的同时牺牲ACF的尖锐主峰，使得AltBOC 信号失去了对多径的鲁棒性。2）子载波相位消除（Sub Carrier Phase Cancellation，SCPC）技术是解决模糊问题的一种创新方法［9］。这种方法以与载波相同的方式去除子载波，产生同相和正交相位的本地子载波，因此接收到的信号既与子载波同相的本地信号相关，又与子载波正交的本地信号相关，然后非相干地组合了相关器的输出，从而消除相关函数的副峰［10］。SCPC 方法的主要缺点是主峰的锐角被破坏，跟踪精度较低；并且由于AltBOC 信号的码片波形较为复杂，SCPC 技术一般不能直接用于AltBOC 信号，需要调整AltBOC 信号的导频分量［11］。3）伪相关函数（Pseudo Correlation Function，PCF）法［12］将多路经过特殊设计的信号分别与接收信号相关得到互相关函数（Cross-Correlation Function，CCF），再经过非线性组合获得无模糊相关函数以消除模糊跟踪问题。文献［6］中描述了基于PCF 方法的无模糊跟踪技术，但是没有对热噪声的影响进行定量分析。

文献［13-14］中提出了组合相关函数方法消除跟踪模糊的基本框架，但都是以正弦相位BOC 信号或者余弦相位BOC信号［15］为研究对象。AltBOC 信号是设计最为复杂的导航信号，对该信号基于组合相关函数方法来设计本地参考信号值得研究。

本文设计了基于组合相关函数的AltBOC 信号无模糊跟踪方法。该方法设计了两个新的多电平码片波形的本地参考信号，并给出了与接收信号的互相关函数表达式。通过将CCF 和ACF 相乘以及线性组合方式，获得了单峰的无模糊组合相关函数，并分析了热噪声下的跟踪性能和抗多径干扰性能。

1 AltBOC调制

AltBOC 调制在E5 频段中传输E5a-I、E5a-Q、E5b-I 和E5b-Q 四个信道［16］，其中：E5a-I 和E5b-I 称为数据通道，而其他两个称为导频通道。本文将AltBOC 调制信号表示为AltBOC（m，n），其中n表示伪码码率fc与1.023 MHz 的比值，m表示副载波频率fs与1.023 MHz 的比值。m和n都被定义为正整数，m≥n，并且比率M=2m/n也是正整数，称为调制系数。

分析AltBOC 调制时，必须具有恒定的包络，否则卫星中的高功率放大器引起的失真将无法容忍［4］。AltBOC（m，n）调制信号采用四级副载波波形，并且当使用四种不同的伪码时，添加乘积项以保持信号恒定的包络。由文献［17］可知，恒定包络的AltBOC（m，n）调制信号的解析表达式为：

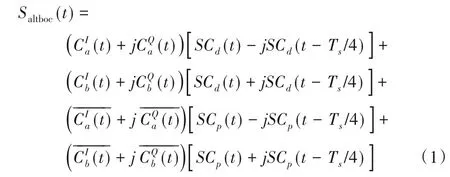
其中：Ts是副载波的周期；SCd(t)是副载波；是包含由伪码调制的导航数据的数据信道的信号分量；和是仅包含伪码的导频信道的信号分量；和副载波SCp(t)是用于获得恒定包络信号的乘积项。乘积项可由式（2）得到：

可以看到，式（1）中后面的两行乘积项没有任何有用的导航信息。

为了方便于公式的推导，有必要分析数据和导频副载波。在本文方法中，所有码片波形都被分成M段，每个段的长度TS=TC/M相等，其中TC是码片波形的周期。因此，数据和导频副载波可以写为式（3）：

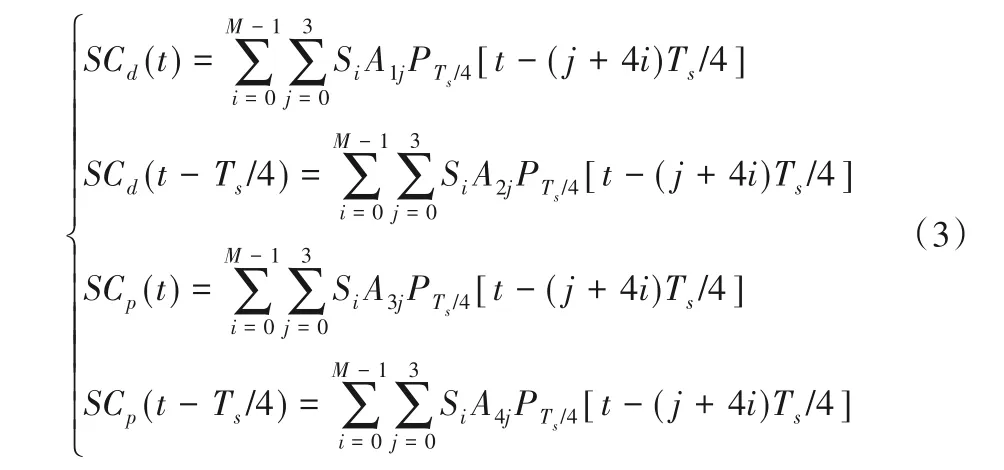
其中：

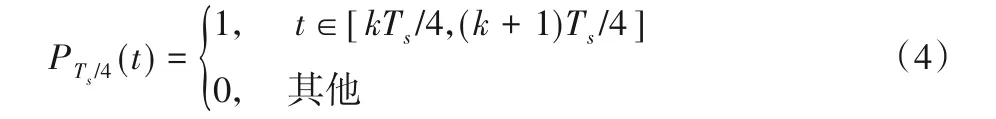
Si是AltBOC信号的扩频波形码符号，定义为：

一般来说，码符号Si可以采用任何实数值。但为了满足码符号序列的能量归一化条件，码符号必须满足Si=(-1)i。而A1j、A2j、A3j和A4j是码符号的参数，用向量的形式表示其具体数值如式（6）所示：

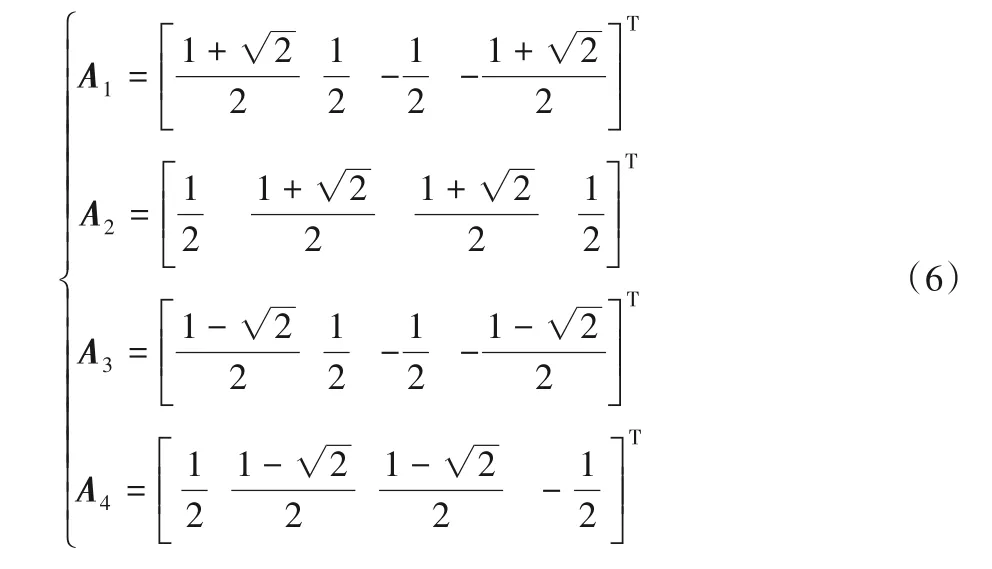
2 本文方法

本文方法和其他跟踪技术之间最显著的区别是本地参考信号调制码符号的区域定义［13］。对于PCF 和其他典型的SCPC 技术，调制码符号定义范围为［0，TC］，而本文提出的调制码符号定义为［-0.5TC，1.5TC］。以这种方式，波形将由相应伪随机噪声（Pseudo Random Noise，PRN）码片的超前、即时和滞后复制码片波形确定。理论上波形可以用更长的间隔来定义，但即使定义范围很宽也不一定能提高提出算法的跟踪性能，并且会降低优化的收敛，因此本文定义范围长度设置为［-0.5TC，1.5TC］。

如果本地参考信号与AltBOC 信号使用相同的伪码，则AltBOC 信号和本地参考信号之间的CCF 等于其调制码符号之间的线性CCF。因此，该问题被转换为设计本地参考信号的调制码符号。由于AltBOC（15，10）信号定义相对复杂，为了方便实现其无模糊跟踪方法，需要使用两个本地参考信号。主要设计思路：设计的两路信号与接收信号相关后分别得到两个在相同的区间内都保留主峰而在其余的区间尽量错开次峰的互相关函数，这样两个互相关函数通过乘法运算就可以保留主峰同时消除多余副峰。由文献［14］可知，在t∈［0，TC-2TS］范围内调制码符号的积分结果为0，那么如果将本地参考信号的调制码符号设计成一个宽度为2TS的矩形，则CCF中的副峰数将明显减少。由于当AltBOC 信号和本地参考信号之间的延迟为0，它们之间的CCF 应该具有最大值，也就是最高的主峰，因此设计了两个宽度为2TS的矩形来确定第一个本地参考信号的调制码符号pl1。由于第一个参考信号和接收信号的CCF依然存在少量副峰，为了消除这些副峰，需要第二个本地参考信号尽量保证与接收信号互相关后，获得的CCF满足前文提到的在相同的区间里保持主峰且副峰正好可以错开。这样可以通过两个CCF的乘法运算来消除这些多余的副峰。根据以上条件要求，可以设计两个形式相对简单的本地参考信号，码符号定义为：

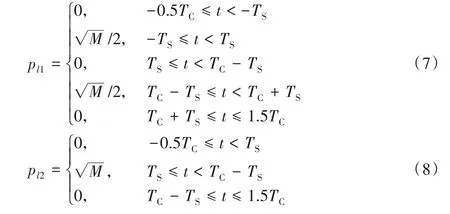
可以看到，上面的两个码符号已经过能量归一化处理，并且pl1、pl2不限于［0，TC］，因此，根据文献［14］，本文称这两个码符号为“等效”码符号，以AltBOC（15，10）信号为例，码符号如图1所示。

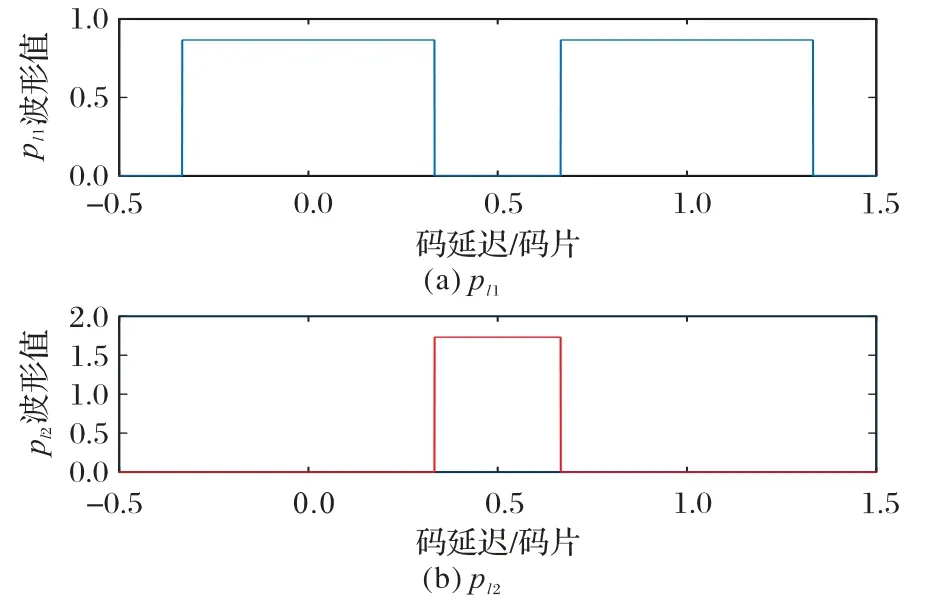
图1 两个本地参考信号的码符号Fig.1 Code symbols for two local reference signals

在带宽足够的假设下，选择不包含数据码并且可以具有更长积分时间的两个导频信道进行更加稳健的跟踪。选择导频信道的信号作为跟踪对象，可以表示为：

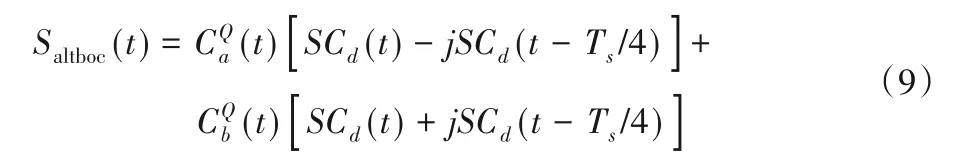
于是，将设计的本地参考信号的码符号和AltBOC（15，10）导频通道信号定义式相乘即可获得以下两个本地参考信号表达式：

由此可以得到对应的两个本地参考信号波形，如图2所示。

图2 本地参考信号波形Fig.2 Local reference signal waveforms

由图2 可知，本地参考信号S1可认为是位于伪码边缘且宽度为2TS的信号。本地参考信号S2可以视为t∈［-TS，TC-TS］的AltBOC信号，在TC的其他位置值都为零。

于是接收到的基带信号与两个本地信号之间的互相关函数可以表示为：

为了实现对AltBOC 信号的无模糊跟踪，需要减少或消除这些多余的CCF 副峰。由接收机性能可知，组合相关函数受接收机设计复杂度和副峰数量的限制，使用较多的CCF 构造组合相关函数虽然会有更好的形状和峰值，但是太多的互相关函数将大大增加实现的复杂性。AltBOC 信号和本地参考信号之间的CCF 应具有尽可能少的副峰，并且在码跟踪过程中使用的组合相关函数必须没有侧峰，即除主峰位置外，其他位置的值应等于零。为了将其他位置的所有峰值设置为零，可以使用乘法中任何数字乘以零等于零的性质，基于此乘法，可以考虑使用乘法运算来抑制不希望的副峰。于是，组合相关函数可以表示为：

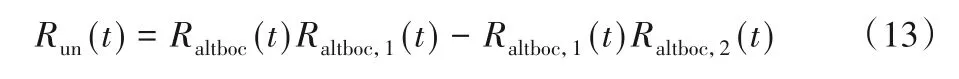
其中：Raltboc，1(t)和Raltboc，2(t)分别是AltBOC 信号与两个本地参考信号的CCF；Raltboc(t)是AltBOC 的自相关函数。图3为两个本地参考信号与AltBOC（15，10）信号的互相关函数，以及由这两个互相关函数得到的组合相关函数。可以看到，得到的组合相关函数出现了两个很小的副峰，但它们的幅度很小，可以忽略。于是，可认为组合相关函数只有一个尖锐主峰，也就是说，组合相关函数是无模糊的。

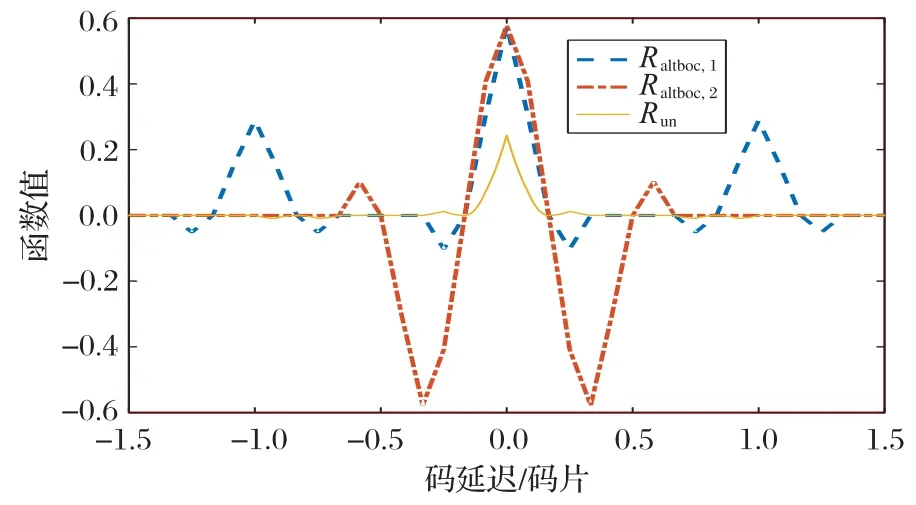
图3 AltBOC（15，10）信号对应的组合相关函数Fig.3 Combined correlation function corresponding to AltBOC（15，10）signal

组合相关函数的码跟踪环路新模型如图4 所示。接收到的射频信号S（t）与本地生成的载波相乘，然后下变频为基带同相（I）和正交分量（Q）。下变频后的I和Q信号分别乘以本地生成的参考信号S1和S2，这些信号由码生成器生成，并且每个码片信号都由式（1）中所述进行调制。

图4 码跟踪环路Fig.4 Code tracking loop

其中，接收机首先生成本地AltBOC 信号以及两个本地参考波形的超前（E）和滞后（L）版本。接收的AltBOC 信号先分别与复现的同相和正交载波相乘，剥离载波。然后，接收信号与本地AltBOC信号的超前（E）和滞后（L）复制码相关，相应的同相相关器输出分别表示为IEaltboc和ILaltboc，正交相相关器输出分别表示为QEaltboc和QLaltboc。同时，接收信号与本地参考信号S1的超前（E）和滞后（L）复制码相关，相应的同相相关器输出分别表示为IE1和IL1，正交相相关器输出分别表示为QE1和QL1。同理，本地参考信号S2对应的分别是IE2、IL2、QE2和QL2。最后，将得到的积分结果发送到提出的非相干超前减滞后鉴别器中。鉴别器输出函数的表达式为：

其中：Δτ表示码延迟的估计误差；d是超前相关器和滞后相关器的间隔；A表示接收信号的幅度。相关器的间隔取0.2TC时，AltBOC（15，10）信号的鉴别器输出曲线如图5 所示。图5中，峰跳（Bump Jump）法是解决模糊问题的一种检测技术，该方法通过对跟踪的峰值和左右邻近峰值进行比较来确定最大峰值。可以看到峰跳法的鉴别曲线实际上是常规超前减滞后的结果，这也是该信号的理想极限情况，一般用来作为对比评价其他方法的理论值。Bump Jump 方法的鉴别曲线存在多个误锁点，导致该方法在实际应用中存在模糊跟踪问题。而PCF 方法、BPSK Like 方法和本文方法的鉴别曲线都是没有误锁点的，即是无模糊的，并且可以看到本文方法的鉴别曲线的斜率比BPSK Like 方法要大，比PCF 方法略小一些，其对应的鉴别器增益也会高于BPSK like 方法低于PCF 方法；同时由于本文方法的鉴别器峰值低于PCF 方法，非零值区间小于BPSK Like方法，这也预示了其抗多径性能的优势。

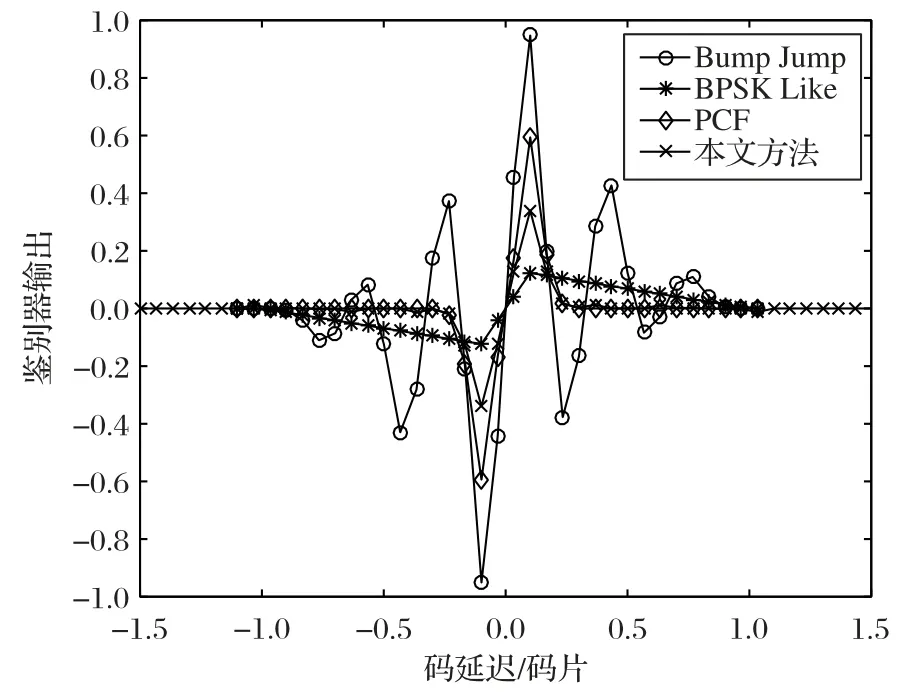
图5 AltBOC（15，10）信号的鉴别器输出曲线Fig.5 Discriminator output curve of AltBOC（15，10）signal

3 性能分析

3.1 热噪声的影响

假设Δθ=0，则相关器输出IE1、IL1、IE2、IL2、IEaltboc和ILaltboc在Δτ=0时满足下列联合高斯分布：

其中μ0和σ分别表示均值和方差，公式如下：

其中：N是独立分布的零均值高斯白噪声过程的双边功率谱密度；Tcoh是码跟踪环路的相干积分时长；R1，1(t)、R2，2(t)和R1，2(t)分别表示本地参考信号S1的自相关函数，本地参考信号S2的自相关函数，以及S1和S2的互相关函数。

由式（16）～（17）可知，假设此时接收机处于稳定跟踪状态时，可以通过蒙特卡洛仿真来获得码跟踪环路各个分支的样本，然后运用统计方式来得到本文方法的鉴别器输出进而获得鉴别器增益的标准差。并且当d=0.2 码片时，本文方法的鉴别器增益大于BPSK like方法。

根据文献［18］所述，闭环码跟踪误差标准偏差σst可通过式（18）获得：

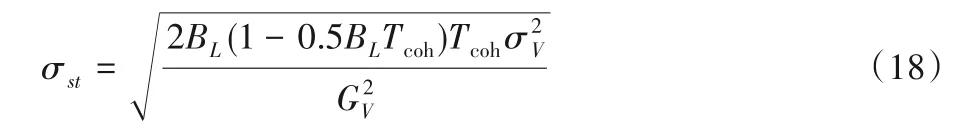
其中：BL是码跟踪环路噪声带宽；σV是鉴别器输出标准差；GV是鉴别器增益。仿真中，设置BL=1 Hz，信号幅度为1，Tcoh为1 ms，相关器间隔d=0.2码片，载波相位差设置为0时，AltBOC（15，10）信号的码跟踪误差分析如图6所示。

图6 AltBOC（15，10）信号的码跟踪误差Fig.6 Code tracking error of AltBOC（15，10）signal

图6 中设置了载噪比C/N 范围是25～50 dB·Hz。在无限带宽情况下，本文方法的跟踪性能优于BPSK Like 方法。本文还分析了Bump Jump、BPSK Like、PCF 方法的码跟踪性能。假设不发生假锁，当信号主峰被正确跟踪时，Bump Jump 法的性能与AltBOC 信号本身一样好，是同条件下该信号的最理想跟踪情况。然而，当环路锁定在错误的峰值时，需要花费一定的时间进行判断，这将降低系统的动态性能，并且Bump Jump法没有消除模糊问题，跟踪性能的优劣和误锁检测技术密切相关，而实际情况尤其是信噪比较低时，Bump Jump 方法存在一定概率的误锁。本文方法中本地信号与输入信号不完全匹配，性能有所损失，跟踪性能比假设完全无跟踪模糊的Bump Jump 方法差一些，但是消除了跟踪模糊。虽说本文方法也存在信噪比损失，但是其码跟踪性能比BPSK Like 好很多，这主要是由于其获得的无模糊相关函数主峰相对较窄，保留了相对较高的鉴别器增益。本文方法在载噪比较低时跟踪性能差于PCF 方法，在载噪比大于40 dB·Hz 时与PCF 方法性能相当。随着载噪比的增加，本文方法与理想值之间的码跟踪误差标准差的差距减小，而且没有任何模糊性威胁，总体上具有不错的码跟踪性能。

3.2 多径抑制性能

多径效应一般被认为是导航卫星信号跟踪过程中的主要误差来源［11］，当存在多径时，多径信号和直达信号进行叠加，导致了相关函数的失真以及鉴别器曲线中过零点的偏移，失真的鉴别器曲线就会有多个过零点，从而产生了跟踪误差。为了研究多径对信号的影响，本文使用了一个通用的多径效应模型，该模型只考虑一条多径信号，并且此多径信号的幅度有一定的幅度衰减以及一定的相位延迟。假设多径的幅度和相位延迟是时不变的，同时设置多径信号与直达信号的相位差为0°或180°，这样可以评估最大的测量误差。

前端带宽设为无限，假设多径直达比为-6 dB，即多径信号的幅度是直达信号幅度的一半，同时设置超前和滞后相关器之间的间隔为0.1 码片。仿真结果如图7～8，分别显示了AltBOC（15，10）信号的多径误差包络和平均多径误差。

图7 AltBOC（15，10）信号的多径误差包络Fig.7 Multipath error envelope of AltBOC（15，10）signal

从图7 中可以看到，当多径延迟小于0.1 个码片时，本文方法对反相多径的抑制效果略差于其他方法，与传统方法的抑制效果接近，但是对同相多径的抑制效果和BPSK Like 方法接近，比PCF 方法略好一点；当多径延迟大于0.1 个码片时，本文方法对多径的抑制效果明显好于其他三种方法，特别是当多径延迟大于0.6 个码片时，能够完全抑制多径，多径误差几乎为零。平均多径误差反映的是方法的整体多径抑制能力，从图8 也可以看到，随着多径延迟的增加，本文方法整体上表现出了很好的多径抑制性能，优于其他几种方法。

图8 AltBOC（15，10）信号的运行平均多径误差Fig.8 Running average multipath error of AltBOC（15，10）Signal

4 结语

本文针对AltBOC 信号设计了两个本地参考信号波形和组合方式，以实现对该信号的无模糊跟踪。分析结果表明，本文提出的方法尽管增加了一定的硬件计算成本，但完全消除了跟踪模糊问题，码跟踪精度总体上优于BPSK Like 方法；并且在多径抑制性能方面明显优于BPSK Like 方法和PCF 方法。进一步工作将考虑从理论上优化本地波形的设计以改善跟踪性能。