基于随机函数的非线性映射保序加密方案

徐衍胜，张游杰

（1.山西军跃迈科信息安全技术有限公司，太原 030006；2.太原鹏跃电子科技有限公司，太原 030032）

（*通信作者电子邮箱zyoujie@163.com）

0 引言

近年来，云计算以其动态扩展、按需服务、按量计费等优势，吸引了众多的企业关注［1］。在软件即服务（Software as a Service，SaaS）成为应用趋势的大背景下，部署和虚拟化在云计算环境中的数据库应用也越来越广泛［2］。与此同时，由于数据存储在云端，用户失去了对数据的直接控制，全部交由第三方云服务提供商进行管理，敏感数据的安全性将难以得到保证，云环境下的数据安全以及隐私保护也成为一个重要问题［3］。为保证数据安全性，一般采用加密的方法，将敏感数据加密后存入云服务器。但是，传统的加密方法多数都不支持直接对密文的运算［4］，如排序、范围查询等。在检索时，必须将云端的大量数据传输到本地，极大削弱了云计算的优势和应用范围。

因此，研究既能保证数据安全性，又能为数据库提供高性能检索的数据加密方法，具有重要的意义。

1 相关工作

1.1 保序加密

保序加密方案（Order Preserving Encryption Scheme，OPES）最早由Agrawal 等在2004 年提出［5］，核心思想为扩域映射，即将明文空间映射到一个更大域的密文空间。由于其密文值顺序与明文值顺序是一致的，因此可以支持对密文数据的最大值、最小值、范围查询，同时可以对密文数据执行group by、order by 等操作。但是，由于数据的有序性，可以给攻击者更多的背景知识。攻击者可以通过获取一些统计信息包括数据频率和数据分布来进行统计攻击［6-7］。同时，该方法需要预先知道数据库中所有被保护数据的值域。当需要对数据库进行插入操作时，该方法仅在理论上具备可行性［5，8］。

在OPES 基础之上，为了从根本上提高保序加密（Order Preserving Encryption，OPE）的效率和安全性，国内外学者进行了大量的研究［8-14］。如Boldyreva等［9］将OPES与超几何和负超几何分布相结合，提出了基于折半查找和超几何概率分布的保序对称加密方法。Krendelev 等［10］基于非退化矩阵概念，提出一种改进的OPES。Martinez等［11］基于网格对角线划分原理实现了保序密文生成。沈楠等［12］综合运用坐标自动网格化处理、保序加密机制、基于身份加密和完整性验证等多种密码学手段，提出了基于保序加密的网格化位置隐私保护方案。

从现有研究成果来看，目前大部分保序加密方案不能隐藏原始数据分布的概率，容易遭受统计攻击，存在安全隐患［13］。为了达到高安全性，许多保序加密方案需要通过使用额外的功能来隐藏密文的顺序并且完成顺序比较，但是这些额外的功能会导致效率的降低。

1.2 保序加密安全性

针对OPES 的安全性能，Boldyreva 等［14］提出一种新的安全性标准：等序明文不可区分IND-OCPA（INDistinguishability under Ordered Chosen Plaintext Attack）。该标准规定，保序加密理想的安全状态等是等序明文不可区分，即：对于2 个序关系相同的明文，攻击者无法区分加密后密文的序关系。根据该标准，经过保序加密后，除了明文顺序信息以外，不应该暴露明文的其他信息。

1.3 线性加密与非线性加密

Liu 等［15］在2013 年首次提出线性加密的基本模型：ax+b+noise。但是该方案安全性很低，攻击者只需要知道2 对明文和密文即可破解线性参数a和b。针对这种情况，Liu 等［15］进一步提出了非线性加密模型af（x）+b+noise。该方法很好地弥补了线性加密的缺点，不会因为重复型数据而让攻击者估计a的大小。

在此基础上，郁鹏等［6］提出了一种基于非线性映射的保序加密方案（nOPE）。该方案根据数据分布的疏密程度来将其划分为多个不同的区间，通过分段函数来确定明文x所在的区间索引i，利用Enc(x)=aix3+bi+δi来实现加密。该方案在高效率的基础上进一步提高了安全性。但是，由于在实际使用中比较复杂，使其应用范围受到了限制。表现在：1）该方案需要预先知道数据集的分布情况，并据此划分区间和设置参数；2）在原始数据集合中插入大量新的数据后，需要再次对数据集进行区间划分，并更改密钥，重新进行加密。

为解决这些问题，兼顾安全性、高效性与易用性，本文提出一个基于随机函数的非线性映射保序加密方案，命名为rnOPE。

2 算法模型

2.1 原理及系统构成

本文方案的基本原理是将明文空间看作一个等差递增数列，数列中每一个元素都映射到一个单独的密文空间。在密文空间的顺序与明文空间一致的情况下，利用随机函数来保证密文空间与明文空间具有不同的分布特征。在加密时，只需从对应的密文空间中随机选取一个值即可作为其密文。

加密系统{D，C，K，E}由明文空间D、密文空间C、密钥K和加密算法E构成。

明文空间D由长度为L的等差递增数列{d1，d2，…，dL}构成，公差为d，满足以下条件：

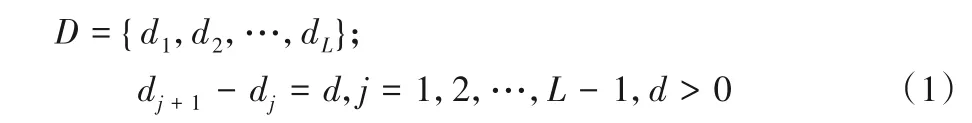
密文空间C由L个长度不同的空间Ci(i=1，2，…，L)构成，每个空间Ci与D中的di一一对应。C满足以下条件：

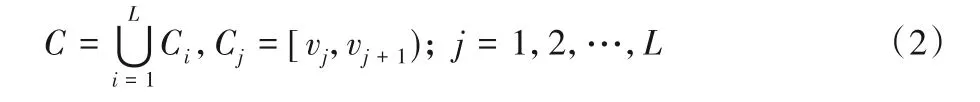
其中：vj和vj+1是空间Cj对应区间的最小值与最大值，{v1，v2，…，vL+1}是一个非等差的递增数列，记为V。

密钥K用于构建密文空间C。

加密算法E用于实现di与Ci的对应关系，并从对Ci中随机选取一个值作为加密后的数据，满足以下条件。

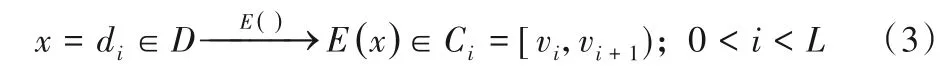
2.2 密文空间的计算

由式（2）可知，密文空间的计算过程实际上是一个确定递增数列V的过程。为使加密前后的数据具有不同的统计特征，V中相邻元素的差值（即Ci的长度）应具有非均匀分布的特征。计算过程如下。

1）初始化密钥K。

①确定一个数值N，N≤L，并符合条件1的限制。条件1的定义见下文。

②确定一个用于构造密钥K的随机数发生函数F（）。每次调用该函数都将产生一个随机数字，这些随机数字在N次内应具有非均匀分布的特征。为达此目的，可对一个均匀分布的随机函数做非线性运算，以破坏其分布特征。同时，明文空间D的各项参数及数值N也可以参与运算，以便每个参数都可以对密钥K产生作用。比如，本文中采用了以下公式：

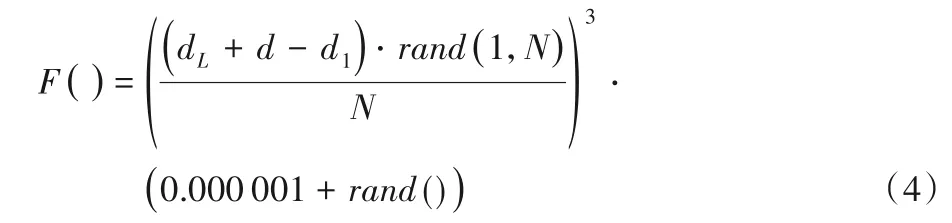
其中：dL和d1分别是D的最大值和最小值，d是构成D的等差数列的公差；rand（1，N）可随机生成整数，0 ≤rand(1，N) ＜N；rand()可随机生成实数，0 ≤rand() ＜1.0。

③连续调用N+1 次F（），生成数列R={r1，r2，…，rN+1}。数列R是一个非等差的递增数列，该数列中每两个相邻的元素构成一个区间Ki(i=1，2，…，N)，进而构成密钥K。K满足以下条件。

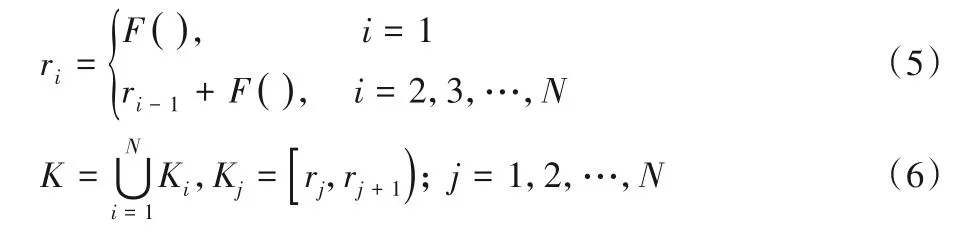
2）利用密钥K生成密文空间。

密文空间C的长度L往往是一个非常大的数字。为了方便编程实现，设计一个函数G，在需要时临时生成所需部分的区间。即

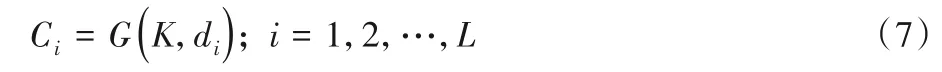
已知某数值x∈D，函数G(K，x)的实现方法如下：

①将明文空间D等分成N个长度相同的明文区间Di(i=1，2，…，N)，作为明文区间初始值，并找出x所在的明文区间；将密钥K作为密文区间初始值，Di与Ki(i=1，2，…，N)一一对应。其中等分是指Di符合以下条件：a）D=；b）所有Di都由一个长度为L/N的等差数列构成，公差均为d；c）Dj的最大值小于Dj+1的最小值，j=1，2，…，N-1。

②判断x所在的明文区间中是否只有1个元素，如果是则此时对应的密文区间即为输出，否则执行以下操作。

③将x所在的明文区间再次等分为N份，并在等分后的区间中找出x所在的区间；将对应的密文区间也分为N份，保证与明文区间的对应关系。其中，密文区间按密钥K中每个元素的长度比例来划分。

④转到步骤②。

根据此方法，规定条件1 为：N必须保证明文空间D中的任意元素在生成对应的密文区间时，上述步骤执行的顺序和次数都相同。

该方法在计算机上的实现过程如下。

①定义参数及变量：（a）定义长度为L的明文空间D，确定其构成参数dL、d1和d的值，并保证x∈D。其中dL和d1分别是D的最大值与最小值，d是构成D的等差数列的公差。（b）定义常量N。（c）定义数组变量M，整数型变量index，实数型变量Mmax、Mmin、Vlen、Vmax和Vmin，用于计算过程中各个中间数据的存储。在计算完成后，Vmax和Vmin用于记录x对应的密文区间，可记为［Vmin，Vmax）。

②将明文空D间平均分为N等份，使用变量M来表示。计算x在M中的索引，存入变量index，计算公式为index=。x所在的区间记为M［index］，最大值与最小值分别存入变量Mmax和Mmin，计算公式为Mmax=d1+(index+1)×(dL+d-d1)/N，Mmin=d1+index×(dL+d-d1)/N。对应的密文区间V［index］的最大值与最小值分别存入变量Vmax和Vmin，计算公式为Vmax=rindex+2，Vmin=rindex+1。其中：rn(n=1，2，…，N+1)是数列R中的元素，函数Int()的作用为取整。以上表述中下标全部从1开始，index从0开始，下同。

③如果Mmax-Mmin≤d，则认为V[index]=[Vmin，Vmax)即是x所对应的密文区间，可以结束运算。

④如果Mmax-Mmin＞d，则执行以下运算。令M=M[index]，然后将区间M平均分为N等份，并继续使用变量M来表示。计算x在M中的索引，存入变量index，计算公式为。x所在的区间记为M［index］，最大值与最小值分别存入变量Mmax和Mmin；对应的密文区间变量V［index］的最大值与最小值分别存入变量Vmax和Vmin，计算公式为Vmax=Vmin+rindex+2×Vlen/(rN+1-r1)，Vmin=Vmin+rindex+1×Vlen/(rN+1-r1)。其中，Vlen=Vmax-Vmin，且Vlen必须在Vmax和Vmin之前进行计算。

⑤转到步骤③。

2.3 加密算法E的实现

加密算法E需要实现从明文空间D到密文空间C的映射，并从对应的密文区间中随机抽取一个值作为密文。公式为：

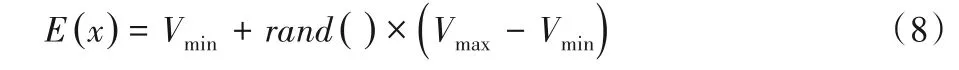
其中：Vmax、Vmin是由函数G(K，x)生成的密文区间的最大值与最小值，满足[Vmin，Vmax)=G(K，x)；rand()可随机生成实数，0 ≤rand() ＜1.0。

3 正确性与安全性分析

从正确性、IND-OCPA 安全和抗统计攻击三方面对rnOPE进行分析。

3.1 正确性分析

在明文空间D中任选两个元素x1、x2，x1＜x2。如果有E(x1)＜E(x2)，则认为方案是正确的。

下面对函数G(K，x)在计算机上的实现过程进行分析。

假定：1）计算一个明文元素的密文空间需要n(n≥0)轮循环；第0轮循环对应过程中的步骤2）。2）每轮循环中，x1对应明文区间的索引记为index1，对应密文区间的最大值记为Vmax1；x2对应明文区间的索引记为index2，对应密文区间的最小值记为Vmin2。

如果x1与x2在第0 轮循环处于不同的区间，则由步骤2）可知，index1 ＜index2，Vmax1=rindex1+2，Vmin2=rindex2+1。由于rindex1+2≤rindex2+1，所以：Vmax1≤Vmin2。

如果x1与x2在第m(m＞0)轮循环时处于不同的区间，则由步骤4）可知，index1 ＜index2，Vmax1=Vmin+rindex1+2×Vlen/(rN+1-r1)，Vmin2=Vmin+rindex2+1×Vlen/(rN+1-r1)，其中Vlen和Vmin分别是上一轮循环中x1与x2所对应密文区间的长度和最小值。由于rindex1+2≤rindex2+1，所以Vmax1≤Vmin2。

综上所述，如果x1＜x2，则对应的密文区间满足条件Vmax1≤Vmin2。根据约定，区间包含最小值，不包含最大值。因此，由式（8）可知，E(x1)＜E(x2)。所以，rnOPE是正确的。

3.2 IND-OCPA安全

假设攻击者能够操纵客户端，并且有顺序关系完全相同的两组数据集D1 和D2。攻击者将这两组数据发送至客户端，操纵客户端对其中一组进行rnOPE 加密。如果攻击者能够通过分析加密结果来判断客户端加密了哪一组数据，则认为rnOPE不满足IND-OCPA；反之则认为满足IND-OCPA［8］。

攻击者用于分辨客户端加密了哪一组数据的条件有三种：根据密文顺序判断、根据单个密文值大小判断和根据明文与密文值变化规律判断。

对于根据密文顺序判断的情况：在rnOPE 方案中，对明文数据集中值不相等元素，对应密文的顺序与明文完全相同；对明文数据集中值相等元素，由于每个元素对应的密文值是一个随机数据，故其对应密文的顺序是随机的。由于数据集D1和D2具有相同的顺序关系，在这两种情况下都无法由密文的顺序判分辨出明文数据集。因此，根据密文顺序进行判断的条件是不成立的。

对于根据单个密文值大小判断的情况：由密钥K的计算公式可知，大小与明文空间D的各项参数及数值N有关。在攻击者不知道这些参数的情况下，无法由密文大小推断出明文值的范围。因此，根据密文值大小进行判断的条件也是不成立的。

对于根据明文与密文值变化规律判断的情况：在本文方案中，无论是密文空间C的划分，还是加密算法E的实现，全部通过随机算法来随机生成。按特定规律分布的明文在经过加密后，除顺序不变以外，将变得没有规律。因此，根据明文与密文值变化规律判断的条件也是不成立的。

由以上分析可知，两组数据加密后，攻击者无法判断对哪一组数据进行了加密。

同时，由密文空间的计算过程可知，对于∀x∈D，对应的密文空间构造函数G(K，x)只与x在D中的位置有关，而与x本身的值无关。因此，通过rnOPE 加密后的结果，除顺序信息外，不会暴露明文的其他信息，所以rnOPE 满足IND-OCPA安全。

3.3 抗统计攻击

假设攻击者能够操纵客户端，并且已知某数据集中明文的数值以及各个明文的数量，攻击者操纵客户端将该数据集进行加密后，存入数据库。如攻击者可以基于明文上的一些统计信息找到密文值和明文值之间的匹配，则认为不能有效地抵抗统计攻击。

统计攻击发生在明文与密文一一对应，且不会改变的情况下［8］。在rnOPE 方案中，由式（8）可知，同样值的明文在每次加密时其结果是不同的。假设某数据集D1的长度为L1，某个值x在数据集D1 中出现的次数为Z（Z＞1），则其频率为Pr(x)=，而对应的密文值频率为Pr(E(x))=。由此可看出，明文值和密文值的频率明显不同。因此，rnOPE 能够有效地抵抗统计攻击。

4 实验与结果分析

为验证rnOPE 的性能，分别做了运算性能实验和正确性与安全性实验。实验环境为：Windows 10 操作系统，8 GB 运行内存，Intel Core i5-4660 CPU @3.20 GHz，开发环境Visual.Net 2010，C#语言。

4.1 运算性能实验

由密文空间的计算过程可知，运算性能与明文空间D的范围、公差d及密钥K的长度N有关。在实际应用中，D的范围与公差d的取值只要能保证要加密的数据集是D的子集即可。基于此，实验方法如下。

明文空间D取值［0，109），公差d=1，长度L=109。设计8组数据集X1、X2、…、X8，各组数据集的长度依次为1×105，2×105，…，8×105，取值方式均为从1开始依次递增1的整数。对每组数据集，分别做三组实验，每组实验所用密钥K的长度N分别取102、104、106。每组数据集的实验过程为：首先随机生成密钥K；然后开始计时，并开始对数据集中的数据依次加密；数据全部加密完成后，记录所用时间。结果见图1。

由实验结果可知，在明文空间D不变的情况下，密钥K的长度越大，加密速度越快。当密钥K的长度N固定时，所需时长与加密数量呈线性关系。密钥长度为100 时，每加密10 万个数据耗时约47 ms；密钥长度为106时，每加密10 万个数据耗时约38 ms。

4.2 正确性与安全性实验

取某一个班级的学生总分成绩作为数据集，长度为37，数据的取值范围在100～800。明文空间D取值［0，1 000）。考虑到成绩可能保留1 位小数，公差d设为0.1，以保证成绩数据集包含在明文空间之内。密钥K的长度N设定为20。对这组数据集采用rnOPE 进行加密，对加密前后的数据进行比较分析，结果见图2～3。

图2（a）给出了学生成绩分布，图2（b）给出了加密后的数据分布。通过对加密前后的数据进行分析，可得出：

1）对于不同的成绩，加密后的顺序与加密前保持了一致。对于相同的成绩，在加密后成为不同的数据。如图2（b）中，有成绩排名靠后的数据大于排名靠前数据的现象。这是因为这两条数据在加密前相等，成绩全为210，加密后的值分别为1.677E+09 和1.692E+09，后者大于前者。由此可知，该方案是正确的。

2）数据加密前后其分布差异很大。如图2（b）与图2（a）相比，在不考虑相同成绩的情况下，两者仅在趋势上相同，都是呈下降趋势。而从下降幅度来看，相邻数据间的降幅差异巨大且无规律。因此，仅通过对密文数据的分析，很难推断出除排名顺序以外的其他信息。由此可知，该方案符合INDOCPA安全。

图2 数据分布Fig.2 Data distribution map

图3（a）给出了学生成绩范围统计分布，图3（b）给出了加密后的范围统计分布。通过对加密前后的统计分布进行分析，可知：

加密前后的数据统计分布特征明显不同：学生成绩在300～400 分人数最多，为11 人；但加密后，在2.5E+09～3.0E+09 次数最多，为16。加密结果明显地破坏了数据的统计分布特征。由此可知，该方案可以有效抵抗统计攻击。

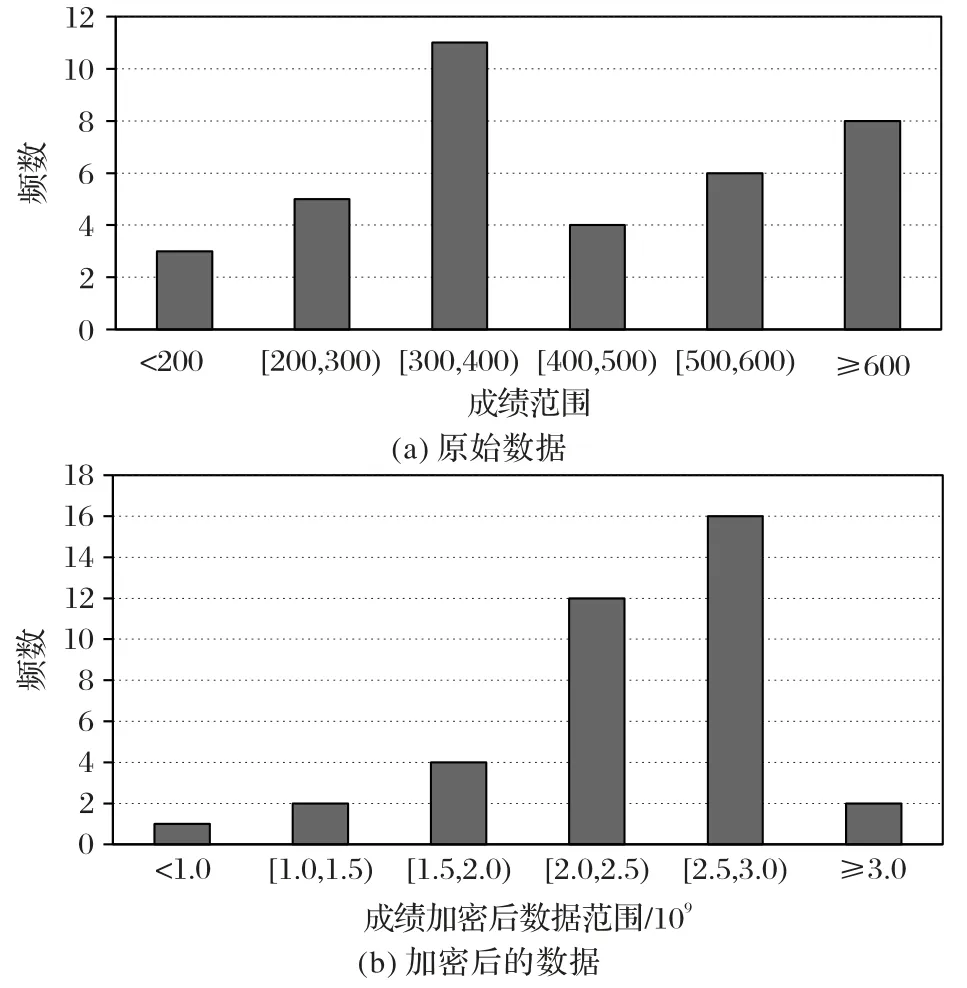
图3 范围统计分布图Fig.3 Range statistical distribution map

4.3 方案比较

在效率、安全性、易用性方面，将本文所提的rnOPE 方案与文献［6］所提的nOPE方案进行对比：

1）在效率方面。rnOPE在密钥长度为106时，每加密10万个数据耗时约38 ms。nOPE 每加密十万个数据耗时约30 ms［6］。考虑到文献［6］未指明实验所需具体硬件环境，可以认为，rnOPE 与nOPE 的加密运算性能处于同一量级，执行时间短、效率高［6］。

2）在安全性方面。rnOPE 达到了理想安全IND-OCPA，并能有效抵抗统计攻击；nOPE 只达到了IND-DNCPA（INDistinguishability under Distinct and Neighboring Chosen Plaintext Attack）［6］，同样能有效抵抗统计攻击。

3）在易用性方面。rnOPE 可采用任何计算机语言实现，可编程性强，同时参数设置简单，适应性强；nOPE同样可编程性强，但参数设置较为复杂，应用范围受到限制。

5 应用场景

本文方案采用了一种不可逆的加密方法，不能提供解密功能。在实际应用中，需要与已知的普通高安全加密算法如3DES（Triple Data Encryption Standard）、高级加密标准（Advanced Encryption Standard，AES）等配合使用，以达到解密的目的。

针对本文方案的应用场景，图4 反映了数据提供者、云服务器、用户之间的数据交互过程。过程如下：1）数据提供者分别使用保序加密算法E和普通加密算法E1 对数据集{d1，d2，…，dn}进行加密，得到密文si和ev，并提交给云服务器存储；2）用户在得到数据提供者授权后，使用算法E对搜索条件参数param进行加密，并且同计算要求type一起发送给云服务器；3）云服务器根据搜索条件，对si进行检索，并将对应的ev返回给用户；4）用户对ev进行解密，得到相应的明文。

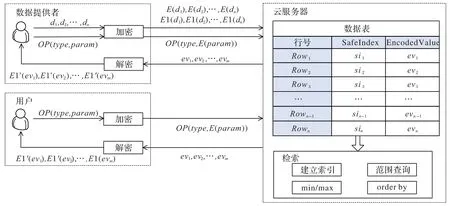
图4 应用场景Fig.4 Application scenario

在此过程中，使用了两种加密算法，加密结果分别在数据表中占用2 个字段。其中保序加密算法E生成的密文si所在字段SafeIndex 主要用于检索，可建立索引，可执行范围查询、最大值、最小值、排序等检索操作；普通加密算法E1生成的密文ev所在字段EncodedValue 不参与检索操作，只将结果返回用户，由用户解密后得到明文。

6 结语

本文方案基于随机函数，通过从明文空间到密文空间的非线性映射实现了保序加密。该方案具有三个特点：1）在保证密文空间与明文空间顺序一致的同时，可有效破坏数据的分布特征，抵抗统计攻击，并且达到了IND-OCPA 安全；2）每10 万个数据的平均加密时间在30 ms～50 ms，加密效率较高；3）方案不需要复杂的参数预设，且可以采用任何计算机语言实现，具有良好的易用性。综上所述，本文方案较好地兼顾了安全、效率和易用性，配合常用的高安全加密算法，可适用于云环境下关系型数据库中数值型数据的加密存储。