雾滴飘移预测试验研究

倪佳胜,茹 煜,王水金,孙笑雪

(南京林业大学 机械电子工程学院,南京 210037)

0 引言

农药使用过程中,控制雾滴的飘移对于林业病虫害防治来说相当关键[1-2],即使用农药防治作物灾害的关键是尽可能减少农药使用中的雾滴飘移量[3- 4]。在喷洒农药的过程中,有很大一部分农药都散失到周围的环境当中,造成使用的效率差[5-7]及农药残留等问题。所以,科学合理地控制雾滴的飘移、减少农药的浪费,有益于生态环境的和谐发展。

雾滴飘移常见的测试方法包括田间测试、模型模拟计算分析、风洞测试分析及飘移测试平台。目前,风洞一般作为雾滴飘移的主要试验场所,试验结果较为可信[8]。至今,国内外学者纷纷进行了大量的基于风洞的雾滴飘移试验。Fritz等[9-10]利用风洞测试不同条件下的雾滴粒径和流场,建立WTDISP模型。Martin等[11-12]在风洞内做试验,得到不同侧风气流下静电喷头的雾滴飘移规律。曾爱军等[13]在风洞内做试验,通过飘移潜在指数DIX的概念分析了在不同温湿度等参数时雾滴的飘移规律。张惠春[14-15]等研究发现:喷头高度、气流速度、喷雾压力的提高都能减小雾滴体积中径,如果采用模型模拟计算分析,利用模型对不同的温度、湿度、风速等自然条件的结果做出预期,可以加强模型的科学合理性[16]。刘雪美等[17]利用CFD模型研究了不同自然风、辅助气流、自身重力及三者之间的互作效应对雾滴飘移的影响。Nuyttens等[18]通过CFD创建出喷雾飘移的仿真模型,得到了农药特性、天气情况、雾滴粒径等相关条件,并通过试验验证了模型的可靠性。Teske等[19]建立了AGDISP和AGDRIFT模型,可以用来预测喷头型号、农药性质、气候及飞机型号等引起的飘移。

本文采用CFD模拟分析法与风洞试验法相结合的方式,开展了雾滴飘移规律的研究。在风洞试验中,对喷雾的采样大多采用棉线、尼龙绳、圆筒等收集方式[20],而笔者提出采用水敏纸采集方法,结合CFD技术[21-23],建立雾滴飘移距离和飘移量的数学模型[24],比较各因素条件下对雾滴飘移的影响,从而可更清晰地反映雾滴飘移的实际情况。

1 模型构建及数值模拟

1.1 几何模型建立

建立以试验所用风洞同等大小的模型为模拟区域,模型长8m、宽2.2m、高2.2m,其模拟布局如图1所示。图1中,Z轴为水平正方向,值为-2.2～5.8m;Y轴为模型高度,取值-2.2～0m;模型宽度沿X坐轴,取值-1.1～1.1m,因此原点坐标为O(0,0,0)。在模拟区域中,采集点所在位置水平方向距离喷头1.8、2.3、2.8、3.3、3.8m,在距离喷头1.8m的竖直方向上采集点分别高0.1、0.2、0.3、0.4、0.5m。

1.2 CFD数值模拟

由于雷诺数Re=ρvd/μ,当v=1、3、5m/s时,Re均大于2 000,因此本文采用CFD中的三维湍流模型来模拟风洞中的气流场,并采用标准k-ε模型。由于雾滴在风洞内气流场中的运动是气液两相流运动,雾滴的飘移受到气流速度、方向的影响,且从喷头喷出的雾滴体积占自然气流体积的比例低于10%,符合CFD软件中对于选择离散相模型的条件。所以,本模拟选用离散相模型,将喷雾作为离散相处理,将自然气流作为连续相处理。

2 试验材料与方法

2.1 试验装置

试验在北京市农林科学院农业智能装备技术研究中心的IEA-1型风洞实验室完成。该系统由低速风洞装置、喷雾系统和采集装置组成。其中,低速风洞装置包括风机和低速风洞,风速范围3～46m/s;喷雾系统包括喷头、流量计、稳压器、泵和水箱等;采集系统由收集架和水敏纸组成。

试验采用日本株式会社KONOMAX多点风速仪,量程为0～50m/s,选择压差流量计控制喷头中的喷雾流量,采用规格为76×26mm的水敏纸收集雾滴。

2.2 试验方法

本试验选用了TeeJet公司的XR11002-VS喷头、DG95015EVS喷头,以及Lechler公司的IDK120-03喷头、LU120-01S喷头,用激光粒度仪测粒径标定出4种雾滴粒径并对其雾滴粒径进行标定,获得风洞内飘移测试所需粒径(100、200、300、400μm)的喷雾压力条件。

在低速风洞内按照图1示意图排布好收集架。每根收集架长1m,在其上均匀放置5张水敏纸;同时,开启喷头和风速控制台,每次开启时间为3s。试验过程中,室内温度和空气湿度保持恒定,试验介质为清水,每组试验重复3次,取其平均值作为最终数据。试验布置实物图如图2所示。

为了研究气流速度对雾滴飘移规律的影响,试验选用雾滴粒径为100μm,喷头高度为0.6m,风洞的气流速度为1、2、3、4m/s,最终结果取3次测量平均值,并要求3次测量标准差小于5%,记录测量结果。在研究喷头高度对雾滴飘移规律的影响时,试验选用雾滴粒径为100μm,风速为1m/s,喷头的高度设置为0.6、0.8、1.0、1.2m;同理,在研究雾滴粒径对雾滴飘移规律的影响时,试验选用风速为2m/s,喷头高度为0.9m,雾滴粒径为100、200、300、400μm。

2.3 计算方法

试验区域雾滴飘移量占比计算方法为

(1)

其中,Adi为1根收集架上雾滴的飘移量;n为1根收集架上放置的水敏纸数量,试验中n=5;di为每根收集架上第i个水敏纸上雾滴的沉积量,数据由iDas Pro雾滴飘移分析系统得到;s为每根收集架上相邻两张水敏纸之间的距离,试验中水敏纸间距离为18cm;w为水敏纸的长度,试验中水敏纸的长度为7.6cm。

(2)

其中,Ad为试验区域的飘移总量;n为放置水敏纸的收集架数量,取n=10,水平方向和垂直方向分别进行求和;Adij为第j根收集架上雾滴的飘移量;s为收集架间的距离,试验竖直距离为10cm,水平间距离为50cm;w为水敏纸的宽度,试验中水敏纸的宽度为2.6cm。

(3)

其中,Ta为总的喷水量;Sd为水敏纸收集到的雾滴飘移量占喷头总喷出的百分比。

3 结果与分析

3.1 数值模拟结果

在气流速度为1、2、3、4m/s,喷头高度为0.6、0.8、1.0、1.2m,雾滴粒径为100、200、300、400μm 的条件下,通过正交实验得到雾滴轨迹散点云图如图3所示。图3中,纵坐标是雾滴在不同水平位置的雾滴轨迹高度。

由图3(a)～(d)可知:随着气流速度的增大,风洞中的雾滴的漂移距离也逐渐增加。当气流速度为1m / s时,大部分雾滴沉积在喷头下面,飘移不明显;当气流速度为2、3m/s时,雾滴受到气流影响有飘移现象;当气流速度为4m/s时,雾滴受到的气流速度过大,雾滴飘移严重。由图3(e)～(d)可知:随着喷头高度的增加,雾滴飘移距离越远。由图3(i)～(l)可知:随着雾滴粒径的逐渐增大,雾滴逐渐主要集中堆积在喷头周围,风洞中雾滴的飘移距离逐渐减小。当雾滴粒径为300μm时,雾滴近似垂直向下喷射,几乎没有飘移,说明雾滴粒径在超过300μm时对于雾滴的飘移距离影响不大。

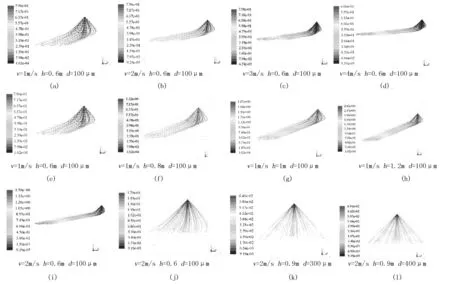
图3 气流速度、喷头高度、雾滴粒径对雾滴飘移的影响

3.2 风洞试验结果及数据对比分析

3.2.1 气流速度对雾滴飘移的影响

不同气流速度下雾滴飘移量占喷施总量的百分比如图4所示。由图4(a)可知:随着距离地面高度的增加,雾滴的飘移量逐渐减少;随着气流速度的变大,雾滴飘移量也逐渐增多。由图4(b)可知:当气流速度为1m/s时,大部分雾滴由于水平力小的原因分布于喷头下方位置,雾滴的飘移过于集中,不利于喷雾作业;当气流速度为2、3m/s时,雾滴的飘移比较均匀,喷雾效果最佳;当气流速度为4m/s时,雾滴几乎消失于测量范围之内,说明雾滴随机飘移距离过大,导致无法有效控制雾滴分布,不利于喷雾作业。

3.2.2 喷头高度对雾滴飘移的影响

不同喷头高度下雾滴飘移量占喷施总量的百分比如图5所示。由图5(a)可知:随着喷头高度的增加,雾滴飘移量逐渐减小。由图5(b)可知:当喷头高度为0.6m时,在喷头正下方的雾滴飘移量占喷施总量的百分比最大,不利于喷雾作业;当喷头高度为0.8m和1.0m时,雾滴的飘移量占喷雾总量百分比呈正态分布,且雾滴的飘移相对均匀;当喷嘴高度为1.2m时,雾滴飘移严重,不利于进行喷雾作业。

图4 不同气流速度下雾滴飘移量占喷施总量的百分比

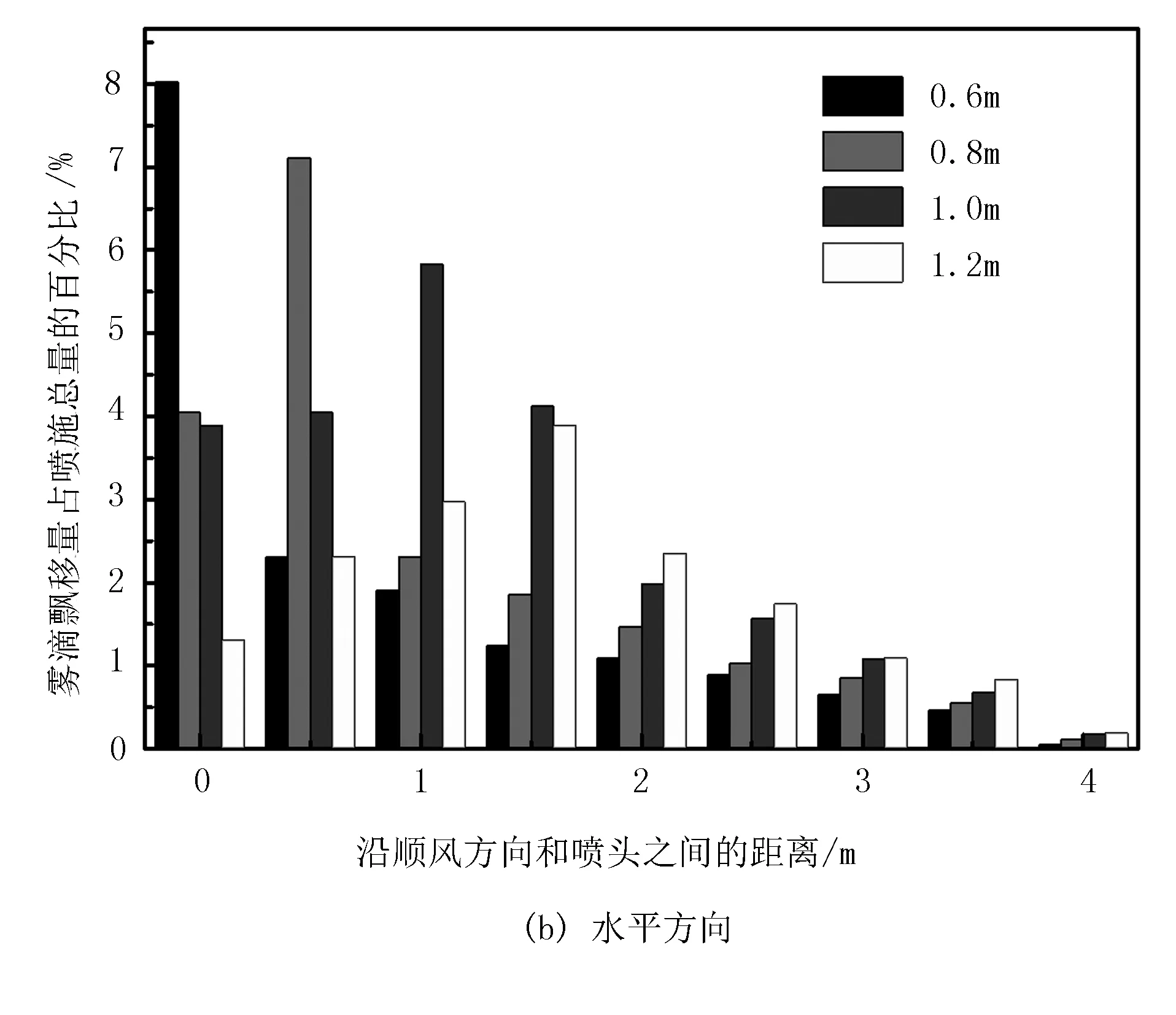
图5 不同喷头高度下雾滴飘移量占喷施总量的百分比

3.2.3 雾滴粒径对雾滴飘移的影响

不同雾滴粒径下雾滴飘移量占喷施总量的百分比如图6所示。

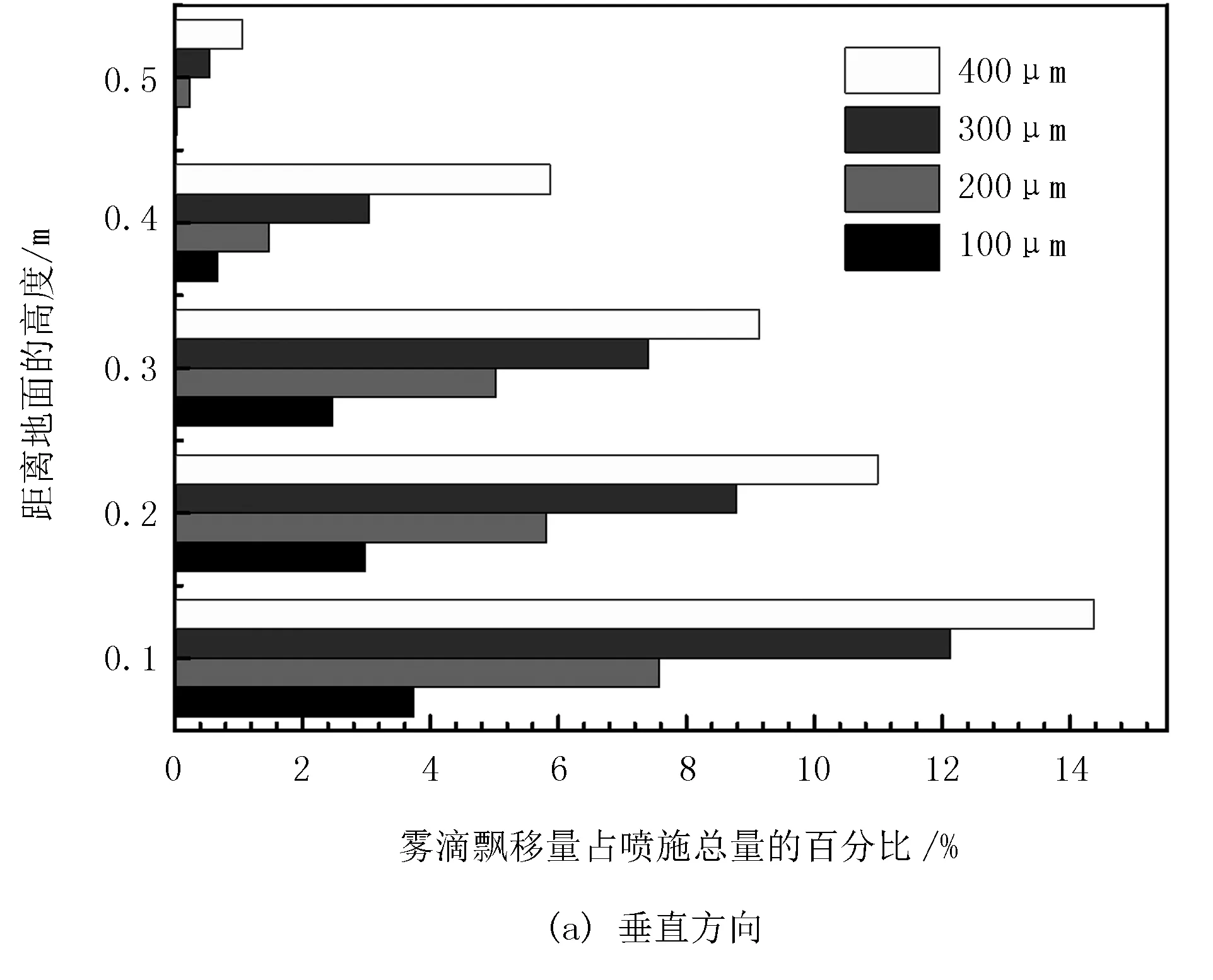
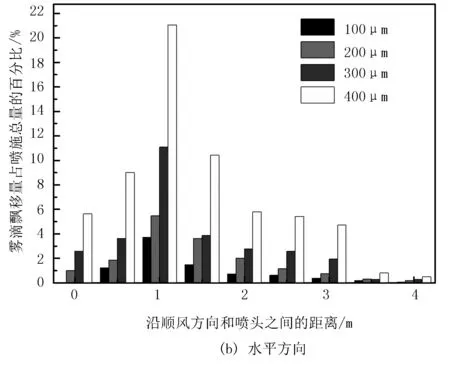
图6 不同雾滴粒径下雾滴飘移量占喷施总量的百分比

由图6(a)可知:随着雾滴粒径的增大,雾滴飘移量也逐渐增大。由图6(b)可知:当雾滴粒径为100μm时,在沿顺风方向和喷头之间的距离4m内的雾滴飘移量占喷施总量的百分比之和不到10%,可推测出雾滴飘移距离很长,不适宜喷施作业;当雾滴粒径为200、300μm时,雾滴飘移总体比较均匀;当雾滴粒径为400μm时,仅仅在雾滴飘移高峰区即距离喷头1m处的雾滴飘移量占喷施总量的百分比就超过20%,说明雾滴粒径在超过300μm时对于雾滴的飘移距离影响不大。

通过以上试验数据和模拟数据对比发现:两者在雾滴飘移研究所得的分析结果大致相似,即可以通过模型模拟来预测雾滴飘移的沉积效果。

3.3 雾滴飘移模型

3.3.1 雾滴飘移距离多元线性回归模型

试验考察了气流速度(A)、雾滴粒径(B)、喷头高度(C)对于飘移距离(P)的影响,利用SPSS的逐步回归法进行分析,建立多元线性回归拟合的方程为

P=0.102A+7.260B-42.244C+20.238

对以上回归模型的拟合度进行检验,经调整后R2=0.706,即飘移距离的变化占总变化的比例为70.6%,证明该拟合方程可以较好地表达变量之间的相关性。

3.3.2 雾滴飘移量多元线性回归模型

试验考察了气流速度(A)、雾滴粒径(B)、喷头高度(C)对于飘移量(Q)的影响,利用SPSS的逐步回归法进行分析,建立多元线性回归拟合的方程为

Q=-2.471A-0.024B-9.616C+17.324

对以上回归模型的拟合度进行检验,经调整后R2=0.839,即飘移量的变化占总变化的比例为83.9%,证明该拟合方程可以较好地表达变量之间的相关性.。

4 结论

1)采用CFD数值模拟技术开展雾滴飘移规律的研究,结果表明:随着气流速度的加快,雾滴的飘移距离增加;随着喷头高度的增加,雾滴飘移距离也增大;随着雾滴粒径的增大,雾滴逐渐主要集中堆积在喷头周围,雾滴在风洞内的飘移距离逐渐减小。

2)风洞试验表明:当气流速度为2、3m/s时,雾滴的飘移比较均匀,喷雾效果最佳;当喷头高度为0.8m和1.0m时,雾滴的飘移量呈正态分布,雾滴飘移总体比较均匀;当雾滴粒径为200、300μm时,雾滴的沉积效果较好。

3)试验结果表明:气流速度、喷头高度、雾滴粒径和雾滴飘移距离具有相关性。通过逐步回归分析,建立包含气流速度、喷头高度、雾滴粒径在内的基于风洞的雾滴飘移距离的多元线性回归模型,以及雾滴飘移量的多元线性回归模型。