风口参数对集热蓄热墙通风及换热特性的模拟研究

赵建会，樊舒雅，崔保天，朱 彬，方子君

(西安科技大学 能源学院，陕西 西安 710054 )

0 前 言

随着社会的发展，越来越多的环境问题逐渐显现，如城市上空出现的雾霾。我国能源结构以化石能源为主，超过30%的社会总能耗用于建筑[1]，能源利用率低。在建筑能耗中，有一部分为采暖能耗。我国传统的供暖方式中提供热源的设备多为锅炉，而使用锅炉供热则大都需要燃烧煤、石油、天然气等化石能源，燃烧后可能会产生污染，且这些能源不可再生。相对的，如果使用可再生的、清洁的能源，如太阳能，就可避免这些问题。使用太阳能可节约资源，而集热蓄热墙就是利用了太阳能达到给室内供暖和通风的目的，集热蓄热墙又称Trombe墙。使用集热蓄热墙可提高能量利用率[2-3]和节能[4-5]。

国内外对于优化集热蓄热墙的通风及换热特性都有研究：王登甲等[5]对青藏高原地区Trombe墙式太阳房进行实验测试，发现Trombe式太阳房的通风口在日出后2～3小时开启，日落前1小时关闭效果最佳。吴彦廷等[6]对太阳能相变蓄热集热墙系统进行模拟，发现系统内空气夹层的流量在一定范围内随空气夹层的宽度增加而逐渐增加，出口温度则随空气夹层宽度的增加而逐渐降低。沈娇等[7]对集热蓄热墙进行二维模拟，通过改变集热蓄热墙通风口的尺寸，对室内温度场，速度场和压力场的分布进行了分析，得出合理选择通风口尺寸有助于提高集热蓄热墙的性能。Burek等[8]搭建了一个的试验台，研究了如太阳能烟囱和Trombe墙的空气换热器的传热和流动特性，发现通过空气夹层的流量与得热量和夹层深度有关，系统热效率与得热量有关，与空气夹层深度无关。Gan[9]使用CFD技术对Trombe墙进行了模拟，研究了空气夹层宽度、墙体高度、玻璃盖板类型及墙体保温对其性能的影响，结果表明，通风率随着壁温和得热量的增加而增加，在夏季运行的集热蓄热墙系统应采取墙体绝热措施。

现有对于集热蓄热墙空气夹层的研究较多，而对于集热蓄热墙的风口的研究还较少。对于通风和供热运行模式下的集热蓄热墙，本文通过改变风口形状、风口面积、进出风口的相对大小来研究有外保温结构的集热蓄热墙风口参数对于其通风及换热特性的影响。

1 理论模型

有外保温结构的集热蓄热墙(见图1)由玻璃盖板、空气夹层、集热结构、保温结构、墙体、上风口、下风口、排风口组成。玻璃盖板和集热结构受太阳辐射后温度升高从而使空气夹层内空气温度升高并产生密度差，继而推动热气流向上自然流动，室内空气则从下风口通过空气夹层由上风口送入室内或由排风口排出。

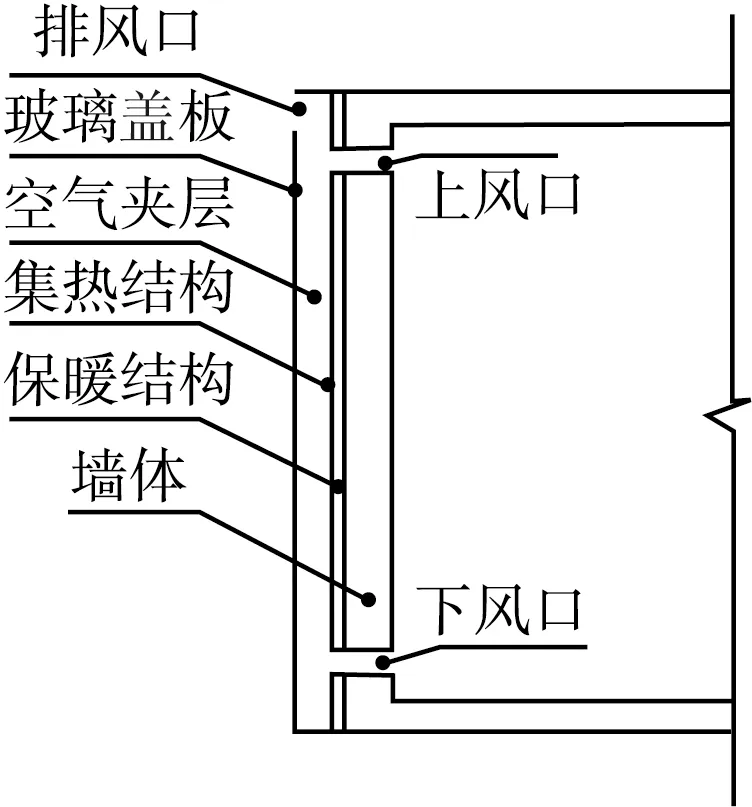
图1 有外保温结构的集热蓄热墙示意图

图2为有外保温结构的集热蓄热墙工作状况示意图。集热蓄热墙的运行大致分为冬季和夏季两种情况，通过调节不同风口的开闭情况来转换冬、夏季运行模式。冬季以供热为主，即室内空气经过空气夹层加热并通过对流换热作用送入室内，同时集热蓄热墙的保温结构也可大量减少热量进入墙体，供热模式侧重于送入室内的供热量。夏季则以通风为主，室内空气由空气夹层内的自然抽吸力排出室外，通风模式侧重流出室内的空气流量即通风量。另外，夏季还可增加遮阳结构来阻止集热。本文着重研究风口参数对有外保温结构的集热蓄热墙的通风和供热效率的影响，从而提高该墙的性能。

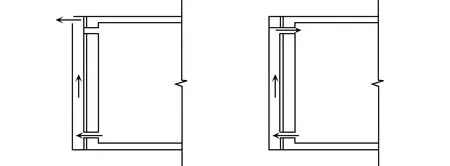
(a)夏季通风模式(只打开下风口和排风口) (b)冬季供热模式(只打开下风口和上风口)

集热蓄热墙空气夹层内空气的流动依靠自然通风作用。自然通风主要依靠室内外风压或热压的不同来进行室内外空气交换。如果建筑物外墙上的窗孔两侧存在压力差△P，就会有空气流过该窗孔，空气流过窗孔时的阻力就等于△P[10]。

(1)

式中，△P为窗孔两侧的压力差，Pa；v为空气流过窗孔时的流速，m/s；ρ为空气的密度，kg/m3；ζ为窗孔的局部阻力系数。

通过窗孔的空气量[10]：

(2)

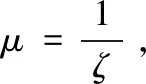
通过空气夹层的换热量：

Q=Cm△t

(3)

式中，Q为通过空气夹层的换热量，W；C为空气的比热容，J /(kg·K)；m为通过空气夹层的质量流量，kg/s；△t为空气夹层的进出口温差，K。

2 物理模型

为了研究夏季和冬季不同工作状况下有外保温结构的集热蓄热墙空气夹层的通风和供热性能，本文根据有外保温结构的集热蓄热墙运行模式设计两个集热蓄热墙空气夹层简化物理模型，如图3所示。图3中下部风口处空气由于热空气自然上升的抽吸作用流入空气夹层，然后从上部风口处流出空气夹层。两个模型的空气夹层厚度均为0.1 m，宽均为1 m，高均为2.8 m，下风口距地面均为0.2 m，其中图3(a)为夏季通风模式下的模型1，只有下风口和排风口。图3(b)为冬季供热模式下的模型2，只有下风口和上风口。下风口均为进口，上风口和排风口均为出口。本文通过改变两个模型的风口参数来进行研究。

(a)模型1

3 数值模拟

本文采用Fluent 模拟软件进行模拟，网格划分采用六面体网格，为了保证对壁面处速度梯度和温度梯度的准确模拟，在壁面处加密网格。数值模拟使用Realizable k-ε湍流模型，壁面处理采用增强壁面函数法。同时为了简化问题，作如下假设：①空气密度符合Boussinesq假设；②不考虑壁面间辐射传热；③不考虑漏风的影响，认为空气夹层除通风口处都密封完好；④传热过程不考虑墙体的蓄热；⑤稳态条件；⑥材料特性与温度无关；⑦不考虑室外风压的影响。

将太阳辐射简化为定热流量模型，当太阳辐射透射过玻璃盖板照射到集热壁面上，空气夹层左右两侧施加的热流条件有相互对应的关系。玻璃的物性参数：吸收系数为 0.06，透射系数为0.85，反射系数为0.09；表面涂层的物性参数：吸热系数为 0.95；则集热壁面每吸收100 W/m2的太阳辐射，玻璃盖板接收的热流为7.43 W/m2[11]。

本文将模型1和模型2的集热壁面的热流密度设为300 W/m2，玻璃壁面的热流密度设为22.92 W/m2，进出口边界条件均为压力边界条件，环境压力均为101 325 Pa, 模型1的进口温度为295 K，出口温度为306 K，模型2的进口温度为287 K，出口温度为287 K。

4 模型的验证

为验证模拟的可靠性，对文献[12]中所述的实验条件下竖直集热板屋顶式太阳能烟囱的自然通风情况进行数值模拟，该实验为一个壁面为均匀的热通量变化的竖直式太阳能烟囱模型，其烟囱高度为2 m，长度为1 m，宽度在0.4～1.2 m，烟囱入口距离地面的高度为0.7 m。该实验模型与本文所述模型基本原理相同，简化该实验模型为一个竖直矩形通道，上下分别为出风口和进风口，该太阳能烟囱宽度取为0.4 m，集热壁面和玻璃壁面的热流密度均按照上述比例给出。

将模拟结果与实验结果进行对比，如图4所示。结果显示，模拟结果与实验结果的变化趋势相同，相对误差为 11.1%～13.1%。这是由于数值模拟与实验所采用的材料及一些环境因素的不同，对通风量有一定的影响。计算结果与实验结果的偏差小于15%，所以，前文中建立的模型，对于空气夹层内的空气流动具有较好的适用性。

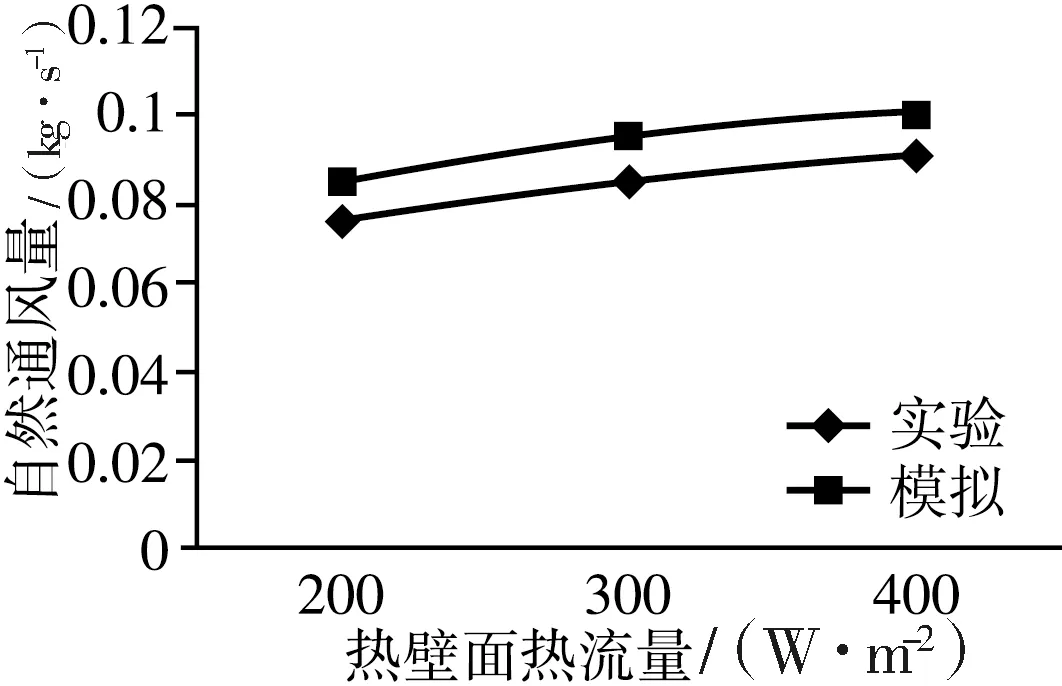
图4 模拟结果与实验结果对比

5 模拟结果及分析

5.1 风口形状对通风及换热特性的影响

为研究风口形状对有外保温结构的集热蓄热墙空气夹层通风及换热特性的影响，在风口的进出风口总面积相等的条件下，设其为0.115 2 m2，分别对于两个模型设定两个风口形状(正方形和长方形)进行模拟。模型1和模型2的边界条件已由前文给出，模型2的“换热量”由式(3)算出。

5.1.1 模型1与模型2的模拟结果

不同风口形状下的模拟结果见表1～2，温度场和速度场见图5～6。

表1 模型1的不同风口形状下的模拟结果

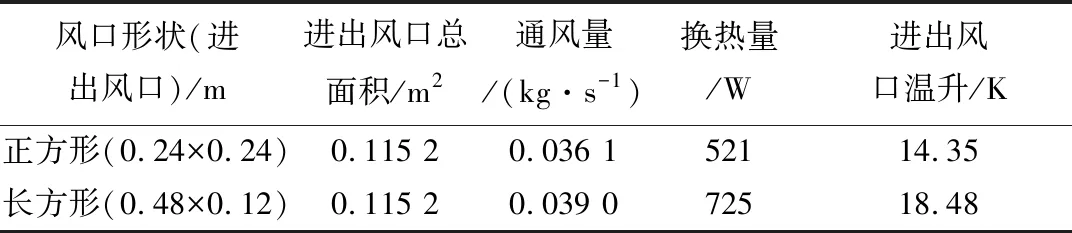
表2 模型2的不同风口形状下的模拟结果

(a)正方形模型的速度场

5.1.2 模拟结果与分析

分析图5～6可得，分别对比长方形风口和正方形风口空气夹层内的温度场和速度场，可知无论是模型1还是模型2，长方形风口空气夹层内的温度分布和速度分布都比正方形风口的均匀，这样可得出长方形风口空气夹层内的通风阻力小于正方形风口，既可增加通风量，又可使空气夹层的换热更加均匀。分析表1～2可得，对于模型1，侧重于通风的情况。相同的进出风口面积下，长方形风口的通风量大于正方形风口，更有利于集热蓄热墙的通风。对于模型2，侧重于供热的情况。相同的进出风口面积下，长方形风口的换热量大于正方形风口，这样更有利于室内的供热。对于以上两种模型，长方形风口的总体性能均优于正方形风口，在实际应用中，可考虑使用长方形风口代替正方形风口。

(a)正方形模型的速度场

5.2 风口面积对通风换热特性的影响(以长方形风口为例)

为研究风口面积对有外保温结构的集热蓄热墙空气夹层通风及换热特性的影响，在风口的进出风口面积相同且风口长宽比为4∶1的条件下，分别对于两个模型设定5个逐渐递增的进出风口总面积参数(进风口和出风口的长宽比例和面积相同)进行模拟。模型1和模型2的边界条件已由前文给出，模型2的“换热量”由式(3)算出。

5.2.1 模型1和模型2的模拟结果(见表3～4,图7～10)

表3 模型1不同进出风口总面积

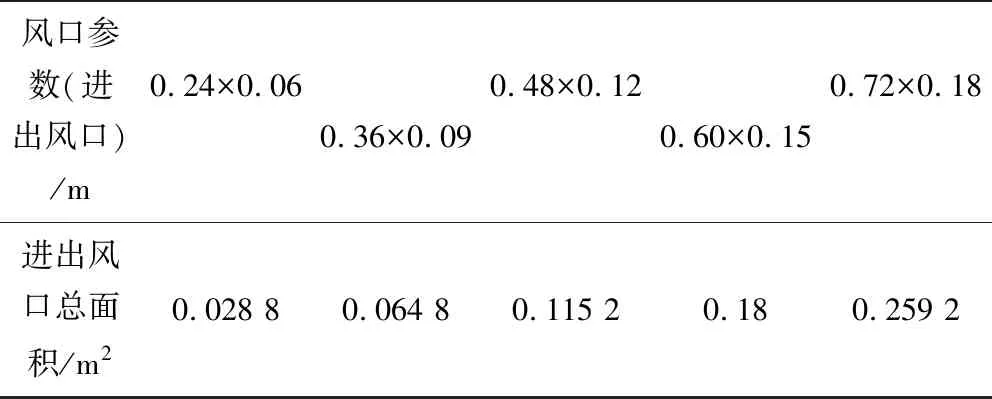
表4 模型2不同进出风口总面积

图7 通风量和进出风口速度

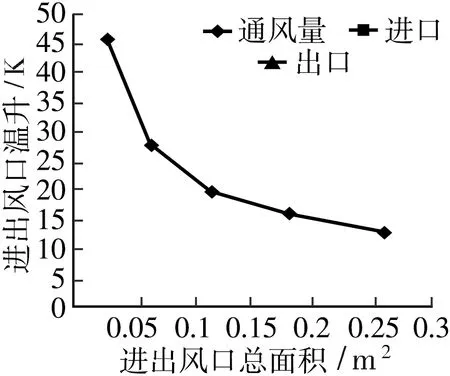
图8 进出风口温升

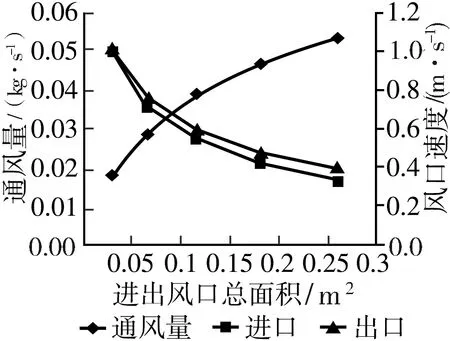
图9 模型2不同进出风口总面积下的通风量和进出风口速度

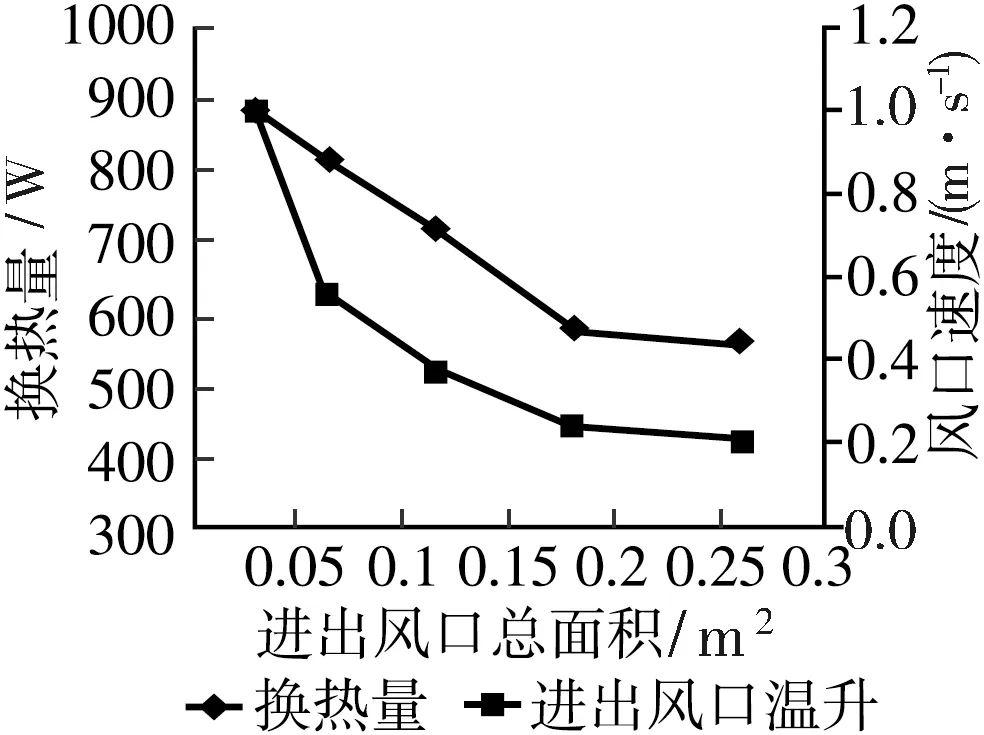
图10 模型2不同进出风口总面积下的换热量和进出风口温升

5.2.2 模拟结果的分析

分析图7～10可得：对于模型1，等比例增加进出风口的面积，随着进出风口总面积的增大，进出风口风速减小，空气夹层的通风量增大，空气夹层的进出风口温升也随之减小，这更有利于有外保温结构的集热蓄热墙的通风；但对于模型2，等比例减小进出风口的面积，随着进出风口总面积的减小，进出风口风速变大，空气夹层的通风量减小，增加了空气在空气夹层的停留时间，换热时间增加，换热更加充分，进出风口温升也随之增大，有外保温结构的集热蓄热墙空气夹层的换热量随之增大，这更有利于其供热。

5.3 进出风口的相对大小对其通风换热特性的影响(以长方形风口为例)

为研究进出风口的相对大小对有外保温结构的集热蓄热墙空气夹层通风及换热特性的影响，在风口长宽比为4:1的条件下，对于模型1以分别以3个方式(B、C、D)加大了进出风口总面积，对于模型2分别以3个方式(F、G、H)减小了进出风口总面积进行模拟。模型1和模型2的边界条件已由前文给出，模型2的“换热量”由式(3)算出。

5.3.1 模型1的模拟结果及分析(见表5，图11～12)

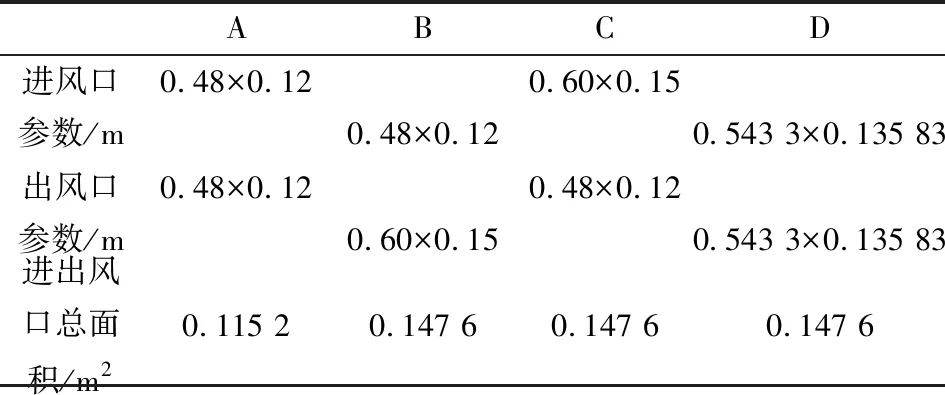
表5 模型1的不同的进出风口面积

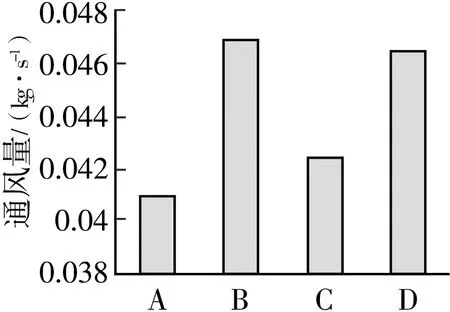
图11 模型1不同进出风口面积下的通风量

图12 模型1不同进出风口面积下的进出风口温升

分析表5和图11～12可得，在风口长宽比为4:1的条件下，以三种方式(B、C、D)加大风口总面积约28%， B、C、D三种方式的通风量都有所增加，B和D分别增加了约14.4%和13.4%，C只增加了约3.7%，增加的相对较少，这是由于C方式的出风口面积小于进风口面积从而增大了通风阻力，所以C方式的通风量增加的不是很显著，同时进出风口温升也没有较为明显变化。但出风口面积大于进风口面积的B方式却是获得最多的通风量的方式，这是由于这种方式可以减小通风阻力，通风量就有所增加，进出风口温升也就随之减少，更有利于有外保温结构的集热蓄热墙的通风。

5.3.2 模型2的模拟结果及分析(见表6，图13～15)

表6 模型2的不同的进出风口面积

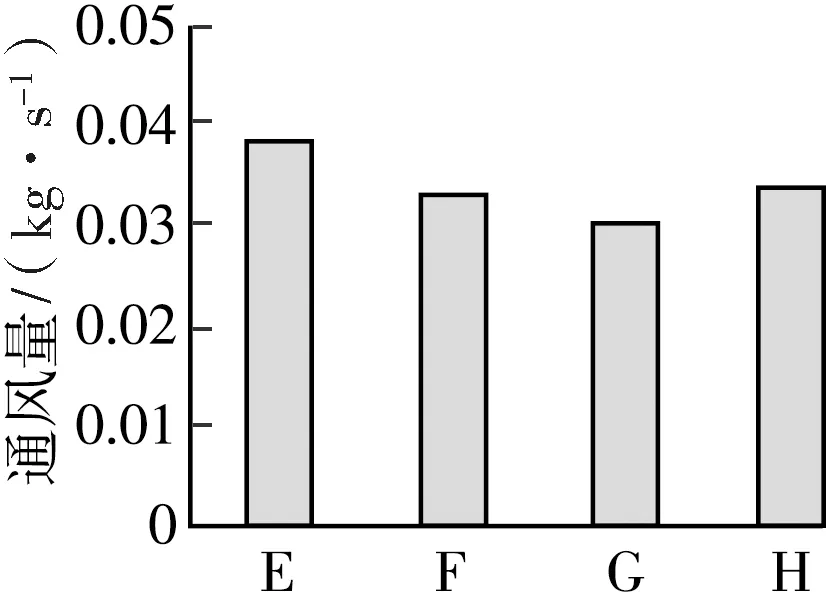
图13 模型2通风量

图13为模型2不同进出风口面积下的通风量，图14为模型2不同进出风口面积下的进出风口温升，图15为模型2不同进出风口面积下的热换量。分析模拟结果可得出，在风口长宽比为4:1的条件下，以三种方式(F、G、H)减小风口总面积约21%， F、G、H三种方式的通风量都有所减少，进出风口温升均有所增加。G方式的换热量增加的最为显著，约12.6%，F和H的分别增加了约-3.6%和4.1%。这是由于F的出风口面积大于进风口面积，通风阻力减小，进出风口温升就增加的较少，加之风口总面积减小则通风量减小，所以F的换热量有所减小；但G的出风口面积小于进风口面积，通风阻力增加，通风量虽有所减少，但换热时间更长，进出风口温升随之增加的较为显著，换热量也就增加的较为显著，更有利于有外保温结构的集热蓄热墙的供热。

图14 模型2进出风口温升

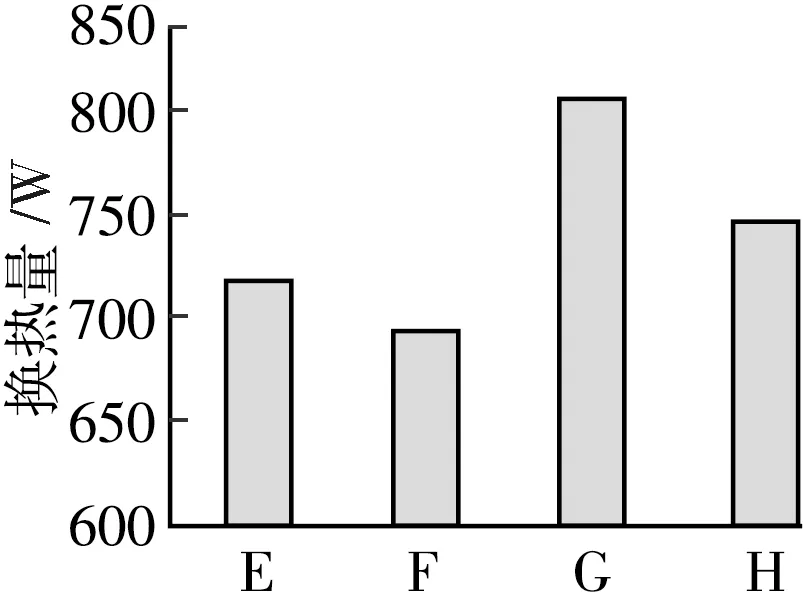
图15 模型2换热量

6 结 论

1)对比正方形风口和长方形风口，长方形风口更有利于有外保温结构的集热蓄热墙的通风和供热。

2)在进出风口相同的条件下，无论是通风模式还是供热模式，增大风口面积可以增加有外保温结构的集热蓄热墙的通风量，但也会减少其换热量。

3)在风口长宽比相同的条件下，对于有外保温结构的集热蓄热墙的通风模式，使用出风口面积大于进风口面积的结构更有利于其进行通风；对于有外保温结构的集热蓄热墙的供热模式，使用出风口面积小于进风口面积的结构更有利于其供热。

4)在实际应用中，可设计有外保温结构的集热蓄热墙的排风口面积大于下风口面积，上风口面积小于下风口面积，以达到最佳的通风和供热的目的。

[ID:010133]