基于改进鸟群算法和极限学习机模型的光伏发电系统输出功率预测研究
饶宇飞, 刘 阳, 李玲玲, 方 舟, 曲立楠
(1. 国网河南省电力公司电力科学研究院, 河南 郑州 450002; 2. 河北工业大学 电气工程学院, 天津300130; 3.中国电力科学研究院(南京), 江苏 南京 210000)
0 引言
化石能源的过度开采和消耗造成了严重的环境污染。人们逐渐重视可再生能源(太阳能、风能、地热能和水能等)的开发和利用。可再生能源的广泛应用有利于减少温室气体的排放, 降低化石能源的消耗[1],[2]。 光伏发电是一种重要的太阳能利用方式,随着科学技术的不断进步,光伏发电技术得到了长足发展。 光伏发电量占我国总发电量的比重呈逐年升高的趋势。 光伏发电对促进我国经济的可持续发展有着重要意义[3]。
光伏发电系统输出功率的预测是光伏发电领域的一项重要技术, 国内外专家对该技术进行了大量的理论研究和数值模拟。 人工智能方法被广泛地应用于光伏预测领域,如BP 神经网络、支持向量机、极限学习机等预测模型。 文献[4]建立了基于遮阳云动态特性的光伏发电超短期预测模型,该模型包括3 个预测阶段:第一阶段选择遮阳云; 第二阶段提取对光伏发电影响较大的目标云的动态特性;最后,通过径向基函数(RBF)神经网络对光伏发电系统输出功率进行预测, 分析结果表明:该预测方法在多云天气下,可以对光伏发电系统输出功率进行精确预测;RBF 神经网络具有较强的映射能力, 但在实际应用中对样本的依赖性很大。 文献[5]提出了一种基于集成经验模式分解(EEMD)和变权组合预测的光伏发电系统输出功率预测方法,该预测方法采用EEMD 将光伏电力数据分解为低频、中频和高频数据;然后,利用变权组合预测模型对这3 组序列的光伏发电系统输出功率分别进行预测;最后,将预测结果进行叠加,得到最终的预测结果,该预测方法可以对光伏发电系统输出功率进行准确预测, 但该预测方法在一定程度上增加了计算成本。 文献[6]提出了基于深卷积神经网络的光伏短期电力预测混合方法, 该预测方法可以减轻光伏并网系统中由太阳辐射不确定性带来的影响, 卷积神经网络适用于处理高维数据, 但卷积神经网络的池化层会导致有价值信息的丢失, 须要通过数据扩增来解决这一问题。 文献[7]基于密度峰值聚类算法并结合Elman 神经网络, 对光伏发电系统输出功率进行预测,分析结果表明,相比于BP 神经网络,Elman神经网络具有良好的动态特性和较快的逼近速度。 文献[8]采用BP 神经网络对3 种天气下的光伏发电系统输出功率分别进行预测,为了提高BP神经网络的预测精度, 采用经典PSO 算法对BP神经网络的参数进行寻优。 为了提高数据缺失情况下, 光伏发电系统输出功率的预测精度, 文献[9]采用双维度顺序填补方法来补齐缺失的数据,并采用广义回归神经网络对光伏发电系统输出功率进行预测。
综上可知, 上述光伏发电系统输出功率预测方法均存在一定的缺陷, 如BP 神经网络易陷入局部最优,模态分解会增加模型的计算成本。为了解决这些问题,本文采用非线性映射能力强、泛化能力强、 学习速度快的极限学习机模型来预测光伏发电系统输出功率。 本文首先分析了极限学习机(ELM)和鸟群优化算法(BSA)的基本原理;然后,对BSA 算法进行改进,提出了改进鸟群优化(IBSA) 算法, 并采用3 个标准测试函数对IBSA算法的收敛性能进行测试;接着,将IBSA 算法的模拟结果与BSA 算法的模拟结果进行比较;最后, 分析了多云天气对光照强度的影响, 建立了BSA-ELM 模型、SVM 模型和IBSA-ELM 模型,并在两种天气下, 利用这3 种模型对光伏发电系统输出功率进行预测。
1 预测模型的构建
1.1 极限学习机原理
极限学习机(ELM)是基于单隐含层前馈神经网络提出的, 具有泛化能力强和学习速度快等优点。 ELM 由输入层、输出层和隐含层组成,其中,输入层和输出层的神经元分别与隐含层的神经元相连接。
隐含层与输入层之间的连接权值ω 的表达式为[10]~[12]

隐含层与输出层之间的连接权值η 的表达式为
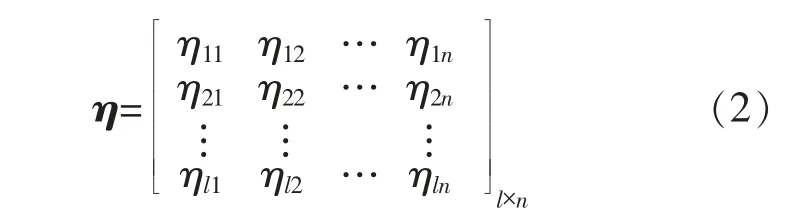
隐含层阈值v 的表达式为
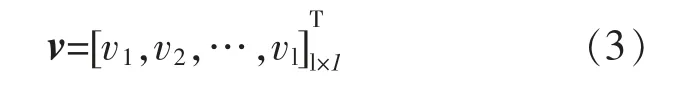
如果有P 个样本集,该样本集的输入C 和输出D 的表达式分别为

假设隐含层的激活函数为A(x),且单隐含层前馈神经网络的输出B 的表达式为
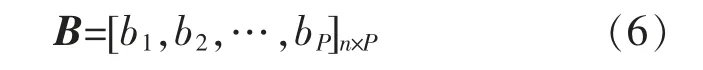
则B 中某一元素bj的表达式为
式(7)可以表示为

式中:L为隐含层的输出。
L 的表达式为

隐含层与输出层之间的连接权值Sη的表达式为
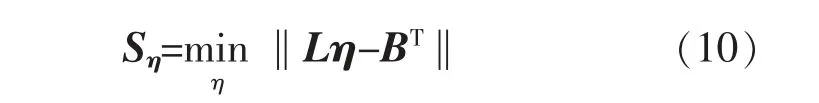
对式(10)进行求解,可得到如下的数值解。

式中:L+为L的广义逆矩阵。
在ELM 的训练过程中,未对输入层的权值和隐含层的阈值进行调整,这样会增加ELM 的隐含层节点数,从而增加预测模型的计算量,降低预测模型预测结果的稳定性。因此,本文采用改进鸟群优化算法对ELM 的输入权值和隐含层阈值进行优化。
1.2 鸟群优化算法及其改进
鸟群优化(BSA)算法是通过模仿自然界中鸟的飞行行为和觅食行为建立的。 BSA 算法遵循以下规则[13]:①每只鸟可以选择觅食行为或警戒行为;②每只鸟可以记录群体中的最优信息和个体最优信息,且信息在群体中是共享的;③当鸟选择警戒行为时,鸟会向群体中心移动,并且在移动的过程中,存在竞争关系;④鸟群会周期性地迁徙到下一个地点;⑤当鸟群迁徙到下一个地点时,选择适应度最佳的鸟作为生产者,将适应度最差的鸟作为乞讨者,剩下的鸟被随机选择成生产者或乞讨者;⑥乞讨者跟随生产者进行觅食。

BSA 算法第2 个规则的表达式为

当鸟选择警戒行为时,其位置的更新公式为
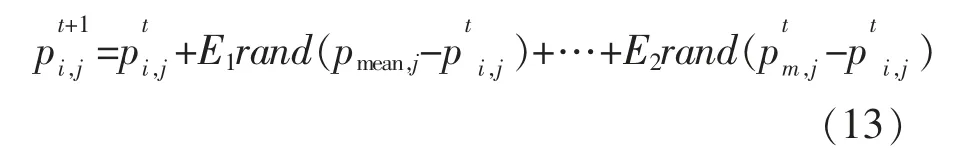
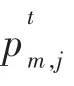
E1,E2的表达式分别为
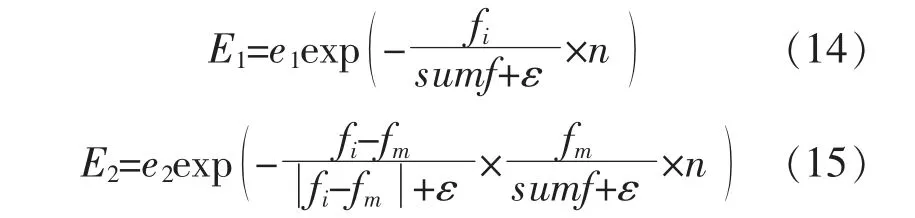
式中:sumf 为鸟群的适应度总和;ε 为无穷小量;e1,e2均为[0,2]内的常数;fi为第i 只鸟的适应度值;fm为第m 只鸟的适应度值。
生产者和乞讨者的位置更新公式分别为

式中:GL 为乞讨者的跟随系数,GL∈[0,2];randn为服从正太分布的随机数。
利用传统的BSA 算法处理维数较高的问题时,容易陷入局部最优解。 本文对BSA 算法进行改进,以提高BSA 算法的搜索能力。 在BSA 中,生产者的觅食能力是最强的,当生产者陷入局部最优时,将会导致整个算法陷入局部最优解。 本文对生产者位置更新公式进行改进,在生产者位置更新公式中引入学习系数,从而提高生产者的搜索能力[16]。 在鸟群中乞讨者的觅食能力是最差的,因此,在寻优的过程中,乞讨者很容易陷入局部最优解。 在迭代后期,本文将变异算子引入到乞讨者位置更新公式中[17],通过变异操作来提高乞讨者跳出局部最优解的能力。
改进后的生产者位置更新公式为

式中:v(t)为生产者的学习系数。
v(t)的表达式为

式中:t 为当前迭代次数;tmax为最大迭代次数;vmax为学习系数最大值;vmin为学习系数最小值。
生产者的学习系数v(t)呈正弦变化,在迭代前期该学习系数较大,从而加强了生产者的全局搜索能力;在迭代后期该学习系数较小,从而加强了生产者的局部搜索能力。 通过引入学习系数,加强了算法的全局和局部搜索能力。
改进后的跟随者位置更新公式为
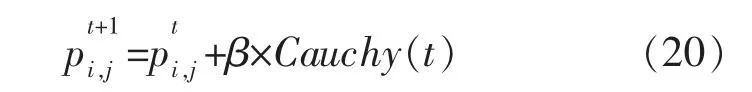
式中:β 为变异的控制程度;Cauchy(t)为服从柯西分布的一个随机变量。
在BSA 算法中,将适应度最好的个体作为生产者,将适应度最差的个体作为乞讨者,剩余个体随机选择为生产者或乞讨者。 这样的选择机制会将适应度相对较好的个体选择为乞讨者,将适应度相对较差的个体选择为生产者,从而降低了算法的收敛速度和收敛精度。 本文针对这一问题在BSA 算法的基础上,提出了IBSA 算法。
IBSA 算法的计算步骤:首先,当鸟迁徙到目的地后,对鸟群的适应度进行排序,并将前4 个个体设定为生产者,最后的3 个个体设定为乞讨者,剩下的个体随机选为生产者或乞讨者。 这样既保证适应度较好的个体被选为生产者,又保证鸟群的多样性。
改进后的生产者和乞讨者的位置更新公式分别为

利用IBSA-ELM 模型对光伏发电系统输出功率进行预测的具体步骤: ①确定训练样本和测试样本的数量; ②将输入的光伏发电系统输出功率数据进行归一化处理; ③将鸟群算法的参数初始化,包括最大迭代次数M,种群数量N,迁徙频率FQ 等;④将鸟群初始化,并计算适应度,确定局部最优个体和全局最优个体; ⑤开始迭代,对ELM 模型的输入层权值和隐含层阈值进行寻优;⑥迭代终止,并得到ELM 模型的最优参数;⑦采用训练好的模型对光伏发电系统输出功率进行预测;⑧采用评价指标对ELM 模型的预测结果进行评估。
2 实验验证
2.1 改进鸟群优化算法(IBSA)的收敛性能测试
为了测试IBSA 算法的搜索能力, 本文采用测试函数对IBSA 算法的收敛性能进行测试,并将测试结果与传统BSA 算法进行比较。 IBSA 算法和BSA 算法的基本参数: 鸟群的迁徙频率FQ为5;最大迭代次数M 为500;种群数量N 为20;学习系数e1,e2均为1.5。
本文采用3 个测试函数对BSA 算法和IBSA算法进行测试,测试次数均为10 次,测试维数均为50。 这3 个测试函数的表达式分别为
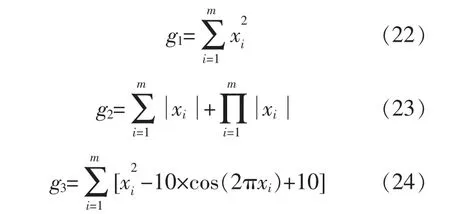
式中:g1~g3均为测试函数的函数值;xi为测试函数的自变量。
g1~g3的 取 值 分 别 为[-100,100],[-10,10],[-5.12,5.12],这3 个测试函数的最优值均为0[18]。本文利用上述3 个测试函数分别对BSA 算法和IBSA 算法进行测试, 得到的测试结果如表1 所示。

表1 测试结果Table 1 Test results
由表1 可知, 利用函数g1进行测试时,IBSA算法收敛到了全局的最优解,但BSA 算法没有收敛到全局的最优值;利用函数g2进行测试时,BSA算法和IBSA 算法均没有收敛到全局的最优值,但IBSA 的收敛精度较高; 利用函数g3进行测试时,BSA 算法和IBSA 算法均收敛到了全局的最优值。 综合比较发现,IBSA 算法的收敛精度高于BSA 算法。
2.2 云遮蔽对光照强度的影响
在影响光伏发电系统输出功率的因素中,光照强度的影响最大, 多云天气又直接影响了光照强度。本文的实验数据来自澳大利亚的DKA 太阳能中心(Desert Knowledge Australia Solar Center,DKASC)。DKASC 位于澳大利亚中部,是一个商业化太阳能技术示范基地。 本文选取2017 年8 月8日(晴朗天气)和10 月7 日(多云天气)9:00-16:00 的测量数据进行分析。
图1 为测试日, 光伏发电系统输出功率和光照强度随时间的变化情况。
由图1 可知, 光照强度与光伏发电系统输出功率存在很大的相关性, 光照强度和光伏发电系统输出功率的变化趋势基本一致, 均呈现出先增大后减小的变化趋势。由图1 还可看出:晴天天气条件下, 光照强度曲线和光伏发电系统输出功率曲线波动幅度较小;多云天气条件下,光照强度曲线和光伏发电系统输出功率曲线波动幅度均较大, 这说明天气状况对光伏发电系统输出功率影响较大。


图1 测试日,光伏发电系统输出功率和光照强度随时间的变化情况Fig.1 Changes of output power and radiation intensity of photovoltaic power generation system with time on test day
2.3 光伏发电系统输出功率预测
本文选用2017 年8 月8 日-12 日 (晴天天气)和10 月3 日-7 日(多云天气)9:00-16:00 的测量数据作为样本数据, 以分析不同模型模拟结果的准确度。 其中,2017 年8 月8 日-11 日的测量数据和10 月3 日-6 日的测量数据作为预测模型的训练样本,8 月12 日和10 月6 日的测量数据作为预测模型的测试样本。
本文分别建立了BSA-ELM 模型、IBSA-ELM模型和SVM 模型,并利用这3 种模型对两种天气条件下的输出功率进行预测。将环境相对湿度、环境温度和光照强度作为预测模型的输入量, 将光伏发电系统输出功率作为预测模型的输出量。
本文采用均方根误差 (RMSE) 和决定系数(R2)作为评价指标,对各模型的预测结果进行评估[19]~[23]。
RMSE 的计算式为

R2 的计算式为
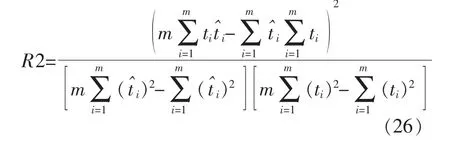
决定系数R2 越接近于1,说明模型输入和输出的拟合效果越好。
2017 年8 月12 日(晴天天气)和10 月6 日(多云天气),光伏发电系统输出功率的实际值,以及利用BSA-ELM 模型、IBSA-ELM 模型和SVM模型得到的光伏发电系统输出功率的模拟值随时间的变化情况如图2 所示。
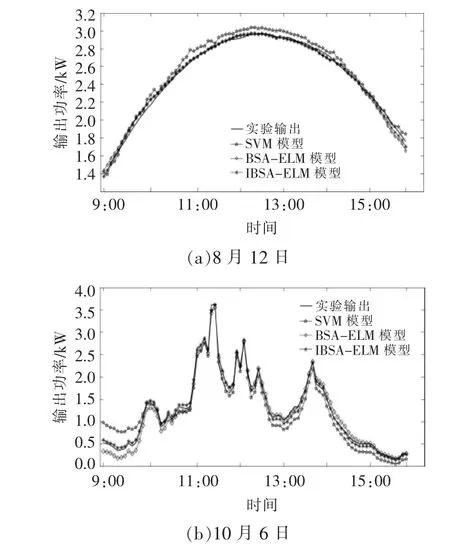
图2 测试日,光伏发电系统输出功率实际值,以及利用不同模型得到的光伏发电系统输出功率模拟值随时间的变化情况Fig.2 Changes of the actual values of the output power of the photovoltaic power generation system and the simulated values of the output power of the photovoltaic power generation system obtained with different models over time on the test day
由图2 可知, 晴天条件下, 利用SVM 模型、BSA-ELM 模型和IBSA-ELM 模型得到的光伏发电系统输出功率模拟值均具有较高的拟合精度,这是由于晴天条件下, 光伏发电系统的输出功率波动幅度较小。 多云条件下,9:00-10:00,SVM 模型和BSA-ELM 模型的拟合精度均较低,而IBSA-ELM 模型的拟合精度较高;10:00-16:00,SVM 模型、BSA-ELM 模型和IBSA-ELM 模型的拟合精度均较低。由图2 还看出,晴天和多云条件下,与其他2 种模型的拟合精度相比,IBSA-ELM模型的拟合精度较高。
2017 年8 月12 日 和10 月6 日,BSA-ELM模型、IBSA-ELM 模型和SVM 模型模拟结果的相对误差随时间的变化情况如图3 所示。
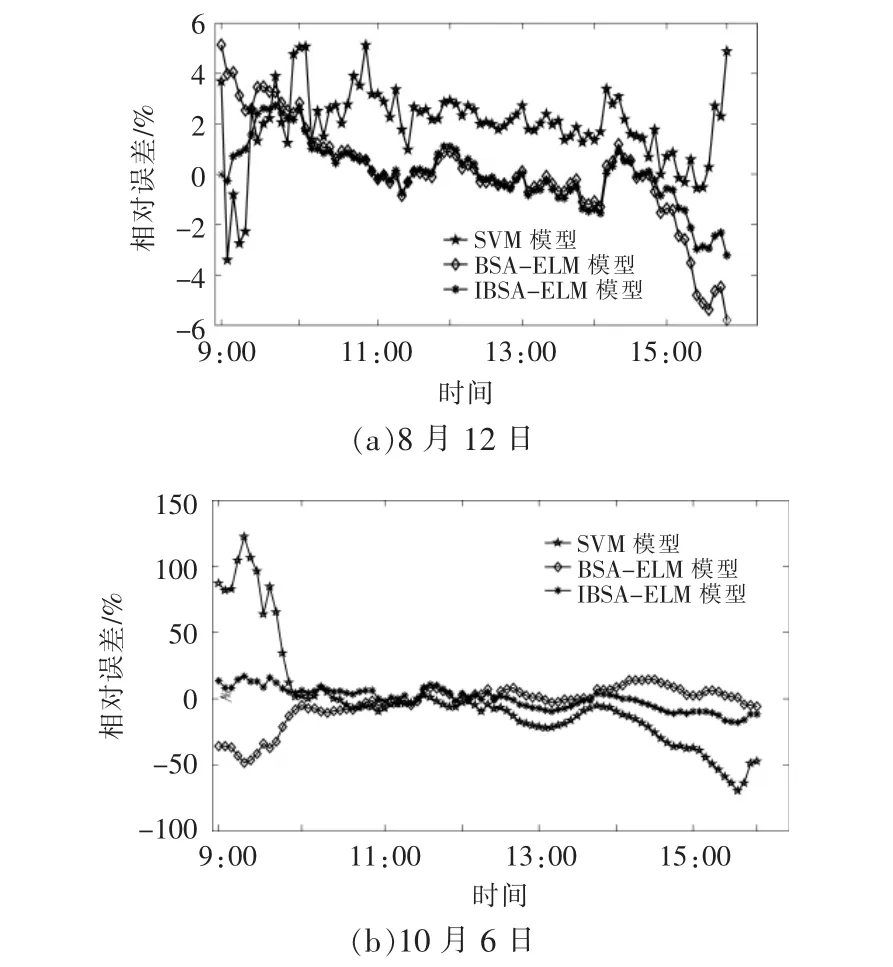
图3 测试日,不同模型模拟结果的相对误差随时间的变化情况Fig.3 Changes in the relative errors of the simulation results of different models over time on the test day
由图3 可知,晴天条件下,3 种模型模拟结果的相对误差均在[-6%,6%]内。 由图3 还可看出,与晴天条件下各模型模拟结果的相对误差相比,多云条件下,3 种模型模拟结果的相对误差较大。此外,根据不同天气条件下各模型模拟结果的相对误差可知,IBSA-ELM 模型模拟结果的相对误差小于其他两种模型。
不同天气条件下,SVM 模型、BSA-ELM 模型和IBSA-ELM 模型模拟结果的精度如表2 所示。表中:NRE为相对误差在[5%,-5%]内的个数;PRE为相对误差在[5%,-5%]内的个数占相对误差总个数的百分比。
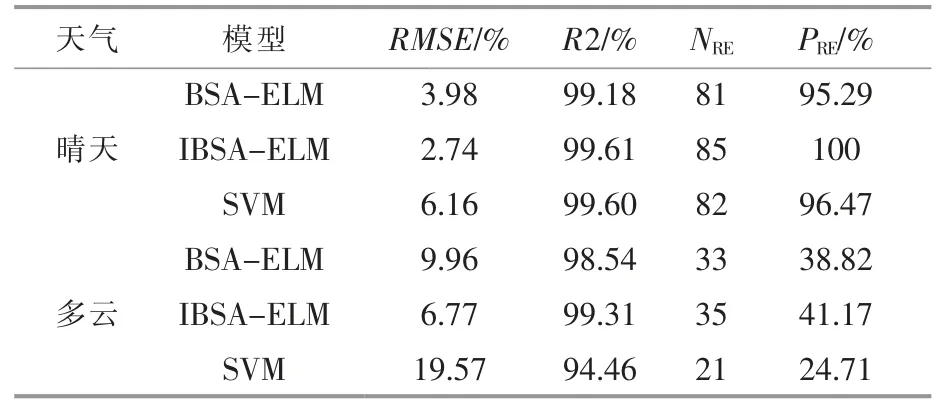
表2 不同天气条件下,3 种模型模拟结果的精度Table 2 The simulation results accuracy of the three models under different weather conditions
由表2 可知,晴天条件下,3 种模型预测结果的精度明显优于多云天气。多云条件下,3 种模型模拟结果的RMSE 约为晴天条件下的3 倍,这说明多云天气能够增大3 种模型的预测误差。此外,晴天条件下, 与SVM 模型和BSA-ELM 模型相比,IBSA-ELM 模型的RMSE 分别降低了3.42%,3.19%。多云条件下,与SVM 模型和BSA-ELM 模型相比,IBSA-ELM 模型的RMSE 分别降低了12.80%,1.24%,这表明IBSA-ELM 模型的预测误差较低。
由表2 还可看出,晴天条件下,3 种模型模拟结果的R2 均在99%以上; 多云条件下,IBSAELM 模型的R2 为99.31%, 其他两种模型的R2低于99%,这表明多云天气使预测模型的拟合效果变差。 此外,不同天气条件下,IBSA-ELM 模型的R2 大于BSA-ELM 和SVM 模型的R2,这说明IBSA-ELM 模型的拟合效果较好。 最后,晴天、多云条件下,IBSA-ELM 模型的相对误差在[-5%,5%]内的个数占相对误差总个数的百分比分别为100%,41.17%, 并且均高于SVM 模型和BSAELM 模型,这表明IBSA-ELM 模型预测结果的稳定性较高。
3 结论
为了准确地预测光伏发电系统的输出功率,本文基于BSA 算法,提出了IBSA 算法,并在两种天气下,利用SVM 模型、BSA-ELM 模型和IBSAELM 模型对光伏发电系统的输出功率进行预测,得到如下结论。
①相比于BSA 算法,IBSA 算法的收敛精度更高,收敛速度更快。
②天气因素对预测模型的预测效果影响较大。 多云条件下,SVM 模型、BSA-ELM 模型和IBSA-ELM 模型的RMSE 均约为晴天条件下的3倍。
③两种天气条件下, 相比于BSA-ELM 模型和SVM 模型,IBSA-ELM 模型的RMSE 较小,表明IBSA-ELM 模型的预测精度较高。 两种天气条件下,IBSA-ELM 模型的R2 均高于99%, 表明IBSA-ELM 模型的拟合效果较好。

