数据驱动的精密双原子分子振动能谱研究进展

付 佳，龙杉杉，蹇 君，钟丽君，罗春润，王 桥，樊群超

（西华大学理学院，四川 成都 610039）

精确的双原子分子振动能谱是研究双原子分子结构和性质的重要基础[1-3]。目前，该方面的纯理论研究主要集中在基于量子力学的各种从头计算法。考虑到实际多粒子体系运动形式的复杂性，从头计算法不得不对多粒子体系的物理模型做简化和近似，如轨道近似等。这些近似的使用造成计算精度的不确定性，同时计算成本很高，人们不得不在精度与体系大小，时间演化尺度方面做精细而复杂的平衡工作。例如Hartree-Fock[4]方法考虑了粒子之间时间平均的相互作用，多组态自洽场方法[5-6](multi-configuration SCF,MCSCF)加入了费米(Fermi)相关、库伦(Coulomb)相关和非动力学相关的影响。多参考组态相互作用[7](multi-reference CI,MRCI)增加了组态函数中的电子相关效应和完整的价组态相互作用。从头计算法发展到现在，已经适用于元素周期表中的大多数元素组合而成的分子，具体计算时，也不需要针对特定体系做过多处理，在应用上已经比较方便。针对双原子分子体系，利用从头计算法，已经可以容易地获得平衡核间距附近的精确势能曲线，为分子动力学、化学和原子分子物理等领域的研究提供了重要的数据支撑。然而由于长程相互作用的复杂性，要获得精确的长程势，尤其是近离解区和离解区的精确势能信息仍然比较困难；因此，目前仍然难以直接通过从头计算法获得高精度的高振转能级信息。

另一方面，针对双原子分子系统，实验上已能通过成熟的光谱学技术[8-10]来测量相应的能级数据。例如：基于傅里叶变换的光谱技术[11]、傅里叶变换微波光谱技术[12-13]、激光诱导荧光光谱技术等[14]。这些光谱测量技术能够测得双原子分子的短程区域分子谱线，但仍然难以获得中长程区域的分子谱线。同时，实验测量数据精度受到环境以及仪器等的影响会有无法避免的不确定度。人们对使用光谱测量技术测得的实验数据进行统计拟合，可以得到一系列光谱常数；但是拟合只能较好地复现已有的实验数据，在用于对实验未能测得的高能级部分进行预测时就会遇到极大的困难。

为了实现对双原子分子振动能谱的精确预测，孙卫国课题组提出了基于实验数据和代数方程的代数法(AM)[15-16]。代数法为固定8阶展开，通过一系列物理判据约束相应的光谱常数，从而达到预测能谱的目的，对多数体系来说其预测结果十分理想。对于一部分AM方法无法处理的体系，该课题组进一步将其优化为可变阶数的代数法，通过扩展模型的表达能力，提高了方法对部分复杂体系的适应性。但对于某些特殊的双原子分子体系而言，由于实验数据误差结构的奇异性，在经过复杂计算后，微小误差被急剧放大，使得预测结果不准确。因此，孙卫国课题组又提出了变分代数方法(VAM)[17]，在选取实验数据时加入一个微小变分项，让其抵消实验误差，从而优化预测结果，达到准确预测的目的。

然而，变分代数法的实现不仅依赖于实验测得的能级数据，还依赖于实验测得的离解能。同能级测量类似，实验测出的离解能也有不确定度，而且相对能级不确定度而言，往往较大，不够精确的离解能数值会使能谱的预测在特定区域产生较大误差[18]。基于我们目前的了解，学界还缺乏对双原子分子体系理论和实验不确定度的严格定量研究。但是从经验上讲，在实验方面，对多电子复杂体系，离解能的测量误差可能会达到数千个波数。比如历史上，实验对于基态CO分子离解能的测量差别极大。最小的离解能实验值为55 821.12 cm-1[19]，而最大的为90 679.1 cm-1[20]，而最近两次测量值的差异也达到了1 063.6 cm-1[19-20]。在理论研究方面，使用从头计算法的不确定度一般也有数千至上万个波数。比如针对基态Br2分子，使用十几种理论配置[21]的计算误差绝大多数都在数千个波数，其中DC-HF方法加pVDZ基组所计算的误差高达12 909.205 cm-1。只有在极少数情况下（NRCCSD(T)方法和pVTZ基组），计算误差能够到数十个波数（66.705 5 cm-1）。

因此，在实验和理论方法目前还无法获取准确离解能的情况下，如何消除离解能不确定度带来的能谱预测障碍，提高能谱预测可靠性，是VAM方法必须要解决的问题。值得注意的是，目前已有一些关于振动能谱的衍生性质研究表明除离解能外，存在着其他可测的物理量(如热容)对全振动能谱也具有敏感依赖性。如果能利用这些关系，采用数据驱动的方法，联合离解能进行交叉验证，可能对VAM方法可靠性的提高大有裨益。

1 整体方法

1.1 双原子分子构成及其哈密顿量

双原子分子由两个原子组成，从结构上说是最简单的分子。双原子分子含有两个原子核，故核外电子在双原子分子中运动时处于多中心场。此外，由于原子核在分子中也有运动自由度，描述分子的内部运动时需要兼顾核外电子和原子核的运动。考虑经典对应，可将分子的平动部分分离，并进一步将剩余部分细分为核的转动、振动和核外电子运动。

按照量子力学的标准求解方法，要获得定量的分子微观运动模式及其演化特性，需要求解分子体系的薛定谔(Schrödinger)方程。若将双原子分子体系中的电子和原子核看作质点，不考虑相对论效应，无外场情况下，则只需求解双原子分子的定态薛定谔方程：

式中：r为电子质点坐标；R为 原子核质点坐标；E为分子体系的总内能；ψ(ri,Rα)为整个分子体系的波函数；为整个分子体系总哈密顿量。

式中：Mα指原子核 α的质量；Zα指原子序数；Rαβ指核 α与核 β的核间距；riα表示核 α与电子i之间的间距；rij表示电子i与电子j间的距离。式(2)中第一项表示核的动能算符：

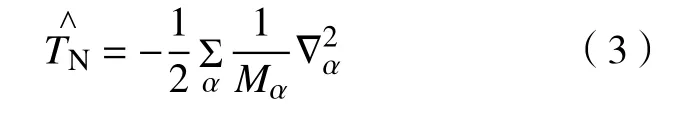
第二项是电子的动能可表示为：

式(2)后三项表示核与核、核与电子、电子与电子之间的相互作用势能：

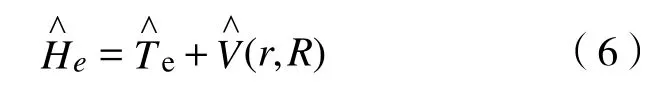
遗憾的是，式(1)在通常情况下并无解析解。而且由于核与电子之间原则上相互影响，对于一般的双原子分子而言，方程的维度可以达到几十甚至上百，使得获得精确的数值解也变得十分困难。因此需要根据双原子分子的特点对式(1)进行近似处理。

1.2 玻恩-奥本海默近似与势能函数

从结果上看，电子的运动速度要远远大于核的运动速度，且原子核的质量远远大于电子质量，电子绕核运动时对核产生微小影响后，核与电子能够迅速实现新的平衡。因此从电子角度看来，当电子调整自己位置时，核在体系中可看作静止不动，即电子在固定的力场中围绕核运动。反过来，当考虑核运动时，核外电子迅速达到平衡，其对核运动的影响就可以通过假设一个与电子坐标无关的等效势替代。核与核外电子的运动特点使得体系中核与核、核与电子的运动可以被分开近似处理，将核与电子之间的相互作用视为微扰势。此方法就是著名的玻恩-奥本海默近似[22]。

另一方面，固定原子核后，在获取等效势时，也需要对电子的多体相互作用问题进行近似求解。原子在形成分子时，其中的大多数电子在整个分子空间范围内运动，在构建描述分子中电子空间运动的波函数时，以单电子近似为基础构建起来的分子轨道理论[23]就是用来描述多电子状态的一种常用模型（对波函数 ψ进行有限展开逼近）。具体到双原子分子，其一部分分子轨道由对称性匹配的2个原子轨道叠加得到。若两核间电子的概率密度增大，能量比原来的原子轨道能量低，例如轴对称轨道(σ轨道)、镜面对称轨道(π轨道)等统称为成键分子轨道。若两核间的概率密度增大，相比于原来的原子轨道能量较高，则不利于成键，例如σ*、 π*轨道等统称为反键分子轨道。还有一种非键分子轨道，其特征是组成分子轨道的原子轨道没有有效重叠，与组合之前原来的原子轨道能量差异不大。总的来说，通过原子轨道线性组合得到分子轨道，需要遵循轨道最大重叠原则、能量近似原则、对称性匹配原则等组合原则。分子轨道中的电子排布则遵循洪特规则、能量最低原理和泡利不相容原理等。

原子中的电子在一个球对称的力场中运动，其运动状态常用主量子数n、角量子数l、磁量子数ml、自旋量子数ms来描述。双原子分子体系由于2个力心的存在，核电场没有球形对称性，只存在绕分子轴对称性。因此，电子的轨道角动量L不守恒，只有轨道角动量L在核间轴方向的分量ML是运动常量，ML的取值为L,L-1,L-2,···,-L。若电场中所有电子的运动方向反向，系统的能量不会改变，ML却变成了-ML。双原子分子中具有相同能量而ML的符号不同的各态称为简并态。L绕分子轴的进动随着电场强度增大也越来越快，造成其轨道角动量意义的缺失；但其在分子轴方向上的分量ML仍存在物理意义。令Λ=|ML|，其中相应的角动量矢量 Λ代表电子轨道角动量沿核间轴的分量，其数值为Λ(h¯/2π)。根据ML的取值可知，对给定的一个L数值，量子数 Λ的取值为：0,1,2,3,···,L。即每一个L的值，Λ都对应着L+1个能量不同的态。按照Λ的取值依次将分子态标记为Σ,Π,Δ,Φ,···[24-25]。

由于电子的自旋与磁场相互作用，双原子分子的电子光谱带具有多重结构。双原子分子中各电子的自旋合成总自旋角动量S，自旋量子数S根据电子数的奇偶性取半整数的奇数倍或者偶数倍。当Λ=0时，电子的轨道运动形成一轴向内磁场，并引起S绕分子轴进动，S在分子轴方向的分量是MS(/2π)。将量子数Ms的绝对值记为Σ，其值为Σ=S,S-1,S-2,···,-S；将总电子角动量标记为：Ω=Λ+Σ，此处Λ，Σ为沿核连线方向，电子总角动量量子数Ω=|Λ+Σ|，当给定 Λ时，Ω共有2S+1个不同值，代表电子态的多重性，如Σ=0表示单重态。根据电子态和分子轨道理论[26]，分子体系总的波函数可以写作：

式中：ψe(ri,Rα)表示电子的波函数，其参数仅受电子状态的影响，相关于核的坐标，独立于核的量子状态；ψN(Rα)表示核运动的波函数，描述体系中原子核的振动和转动。

由玻恩-奥本海默近似，假定核的相对位置R静止不动，哈密顿算符中的核动能项便可以看作为常数。联立式(1)、式(2)、式(6)和式(7)，得

将式(6)、式(7)和式(8)代入式(1)中

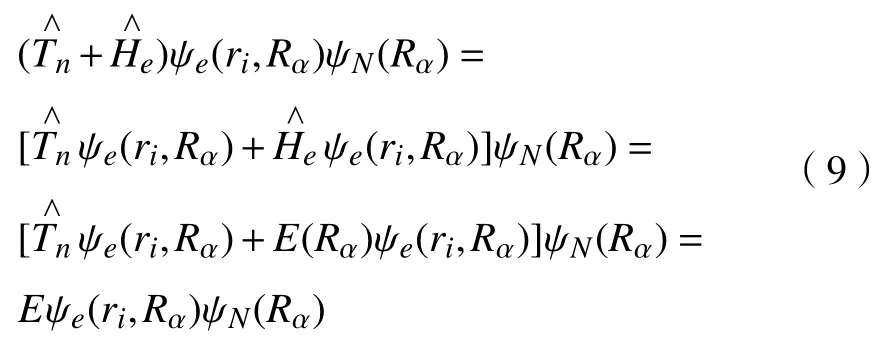
两边同时除以ψe(ri,Rα)，可以得到

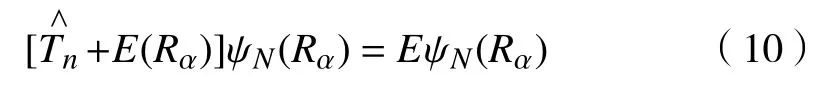
将式(10)与式(8)对比可知，E(Rα)既是当体系中原子核固定时，电子的本征能量，也是体系的势能函数。

1.3 振动能级展开式

从玻恩-奥本海默近似出发，利用二阶微扰求解薛定谔方程，可获得只含光谱常数的双原子分子体系振动能谱的多项式展开表达式[15-17]：

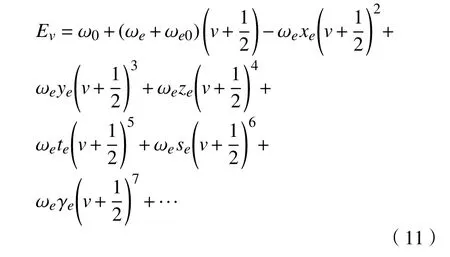
式中：(ω0,ωe,ωe0,ωexe,ωeye,ωeze,ωete,ωese,ωeγe)是分子振动光谱常数；v是振动量子数；Ev是振动能级。式(11)与Herzberg表达式相比，多出了ω0和ωe0两个微小项，其表达式为：

式中的f表示力常数，其大小反映了化学键的振动难易程度。力常数为正表示原子间的作用力是排斥力，为负则表示原子间的作用力是吸引力。由式(11)可知，只需要确定光谱常数，就可以得到分子的全部振动信息。因此，课题组致力于通过实验、理论等各种信息获取这些精确的光谱常数，达到预测能级的目的。

2 计算方法

2.1 代数方法

孙卫国课题组在双原子分子体系纯振动能谱公式的基础上提出了求解双原子分子体系振动能谱的代数方法，即AM[15-16]（algebraic method）方法。将振动能谱公式(11)写为矩阵形式：

式中：Aυk为系数矩阵；X为光谱常数矩阵；E为振动能级；v是振动量子数。

在AM方法中，从振动能谱公式的展开式中选取前八项，从已知的实验能级数据中随机选取8个代入式(14)中进行求解，可得到光谱常数矩阵X。将光谱常数代入式(11)中，则可计算得到双原子分子的完全振动能级。在选取数据时，随机从n个实验数据中选取8个数据，则有种选法，若将每种可能情况分别计算后进行比较，会耗费大量时间且浪费计算资源。因此，需要一组判据，用于挑选出最合适的一组实验数据，拿来预测双原子分子的整套能级。判据如下：

其中：“exp”表示实验测出的数据；“cal”表示用AM方法算出的数据；Evmax为实验测出的最高能级；De表示离解能；表示用实验数据的最高3个能级算出的离解能。

挑选实验数据时，找到符合式(16)—式(22)的1组实验数据，代入式(12)求解矩阵方程得到预测的振动能谱。值得注意的是，AM方法中固定选取振动能谱展开公式的前8项以及选取8个实验能级数据来预测全谱的模式并不适用于所有双原子分子体系。对于一些特殊的双原子分子体系来说，振动能谱公式采取8阶展开并不能得到精确的振动能级全谱。研究者要根据不同体系，选择合适的展开阶数，并选取相应数量的实验能级数据，用于预测完全振动能级。

2.2 变分代数方法

事实上，在使用可变阶数的AM方法进行预测能谱时，由于实验测得的能级数据具有一定的微小误差，在经过复杂运算之后则会放大这个误差，导致预测出的双原子分子的振动能谱不够精确。

为了抵消实验数据所存在的误差，在选取数据点(vi,Evi)(vi为选取的实验数据所对应的振动量子数，Evi为选取的实验能级数据)时，可以加入微小的变分项δE，将可变阶数的AM方法优化为变分代数方法（variational algebraic method,VAM）[17]。此时，式(14)变为

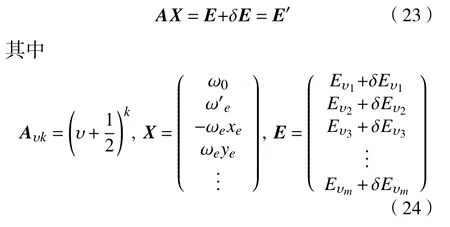
式中，m为VAM方法中所选取的振动能谱展开式的阶数，根据不同体系，m的值不同。同时，加入的微小变分项δE要满足

因此，在VAM方法中，从n个已知实验能级数据中选取m个组成计算子集[Ev]，共有种选法，依次将每个子集中的m个数据都做3次变分试探(-δEvm,0,+δEvm)，这样原来的个子集就变为了N=·3m个子集。此时，将这些子集依次代入式(25)中求解，并利用判据(18)—(24)挑选出N个子集中最好的1组，由此便能预测双原子分子的完全振动能谱。

3 应用与讨论

3.1 PO分子的完全振动能谱

表1所示是用VAM方法预测出的PO分子在X2Π态时的完全振动能谱。

由表1可知，使用VAM方法预测出的PO分子的能级与实验能级相比，误差很微小，并且预测出了振动量子数从0到61的整个振动能谱。然而，当离解能在误差允许范围内产生变化时，预测出的能谱也会随之改变，如表2、表3所示，分别为PO分子的离解能减去5 000 cm-1和加上5 000 cm-1时的振动能谱。

由表1、表2、表3可知，当离解能发生变化时，不同离解能对应的计算能级与实验能级之间的误差并不一致，离解能不确定度会影响能谱的预测精度，在离解能附近区域影响更严重。而离解能通常的测量和计算误差有可能在10%左右。因而完全依赖于实验离解能来计算振动能谱可能会影响其计算可靠度，特别是对高振动能级更是如此。

总的来说VAM方法将有限的实验振动能级与严格的理论计算相结合,通过严格求解代数方程和使用正确的物理判据可以获得双原子分子各电子态的完全振动能谱。由于以实验能级为基础，VAM方法对大多数振转能级的预测可以达到与实验相匹配的精度。但是由于目前的离解能测量精度要远逊于振动能级[18]，会导致在预测整套分子振动能谱过程中，对靠近离解能区域的能谱处理相对不那么可靠，进而可能影响相应的衍生分子性质的研究（例如对热力学量的计算）。并且，对于一些双原子分子体系来说，通常存在着实验离解能数据缺失的问题，这将导致无法使用VAM方法预测相应的振动全谱。

3.2 可能的改进策略

针对离解能具有不确定度以及某些双原子分子还没有实验离解能数据的情况，采用最近大放异彩的数据驱动方法[29]有希望在一定程度上弥补这一不足。数据驱动方法是将大量的数据分为训练集和测试集，并产生合适的模型，通过对训练集数据的学习，达到预测未知数据的目的，最后用测试集评判模型的好坏。对于双原子分子体系来说，离解能具有一定的不确定度，在此情况下使用VAM方法预测的振动能谱会有一定的风险。为了降低来自离解能的影响，根据数据驱动方法，需要引入更多的数据扩充数据集用于提取更多的交叉信息来提高模型稳健度。所以，VAM方法需要扩展其使用数据的类型范围，并改进搜索算法，通过利用新的数据类型（例如热容等）来降低离解能不确定度带来的影响。

总的来说，为了得到更加可靠的结果，利用数据驱动的思想，结合变分代数方法(VAM)[17]，除了实验数据以外，由Hartree-Fock[4]自洽场方法、密度泛函理论(DFT)等方法得到的理论数据也可加以利用。另一方面，结合VAM方法的特点，还可以尝试通过多模型融合，关联能级和波函数信息，进一步拓展VAM方法的研究范围，使其除了应用于预测精确的振动能谱及其不确定度外，还可以获得体系的波函数及其他衍生性质。

4 结论

近年来，研究双原子分子的实验技术和理论方法已取得了很大的进步。实验上，已经能够通过成熟的光谱学技术来探测谱线，得到低激发态的精密能级数据，但仍然难以获得高振动激发态的能级数据。特别地，对离解能的探测还远远落后于振动能级的研究。理论上，基于从头计算的理论方法不依赖经验参数，在分子平衡核间距附近取得了较好的结果，能够得到与实验相媲美的精度；但其在近离解能区域的计算结果仍然不够理想，对离解能的计算也存在着较大误差。

表1 PO分子的完全振动能谱

从现阶段来看，仅基于实验方法或者仅基于理论方法的改进已经很难提升精度，针对这一现状，孙卫国课题组提出固定8阶展开的AM方法，将有限的实验振动能级与严格的理论计算相结合，通过严格求解代数方程和使用正确的物理判据从理论上获得双原子分子电子态的完全振动能谱。该方法是现有从头算和实验方法的有力拓展。在此基础上，为了适配更多的分子体系，将AM方法优化为可变阶数的AM方法。进一步，为了控制实验所测数据的误差带来的影响，通过在可变阶数的AM方法中加入微小变分项来抵消实验误差，AM方法演化为VAM方法，提高了计算精度。然而，VAM方法在分子能谱预测时并没有考虑离解能的误差影响。而实际上实验所测离解能的不确定度往往可以达到数百个波数，这会导致能谱预测过程中产生大的不确定性；因此，为了进一步提高VAM方法可靠性，可能需要基于数据驱动的思路，通过扩展VAM方法的可用数据类型（如热容等）来控制离解能的不确定度带来的负面影响。同时通过交叉多项数据来源的信息，VAM方法的应用范围有望被进一步拓展，使其有可能用于预测波函数等更丰富的分子信息。

表2 PO离解能减去5 000 cm-1时的完全振动能谱

表3 PO离解能加上5 000 cm-1时的完全振动能谱

续表3