基于遗传算法智能改进优化蚁群算法

◆宋杨

基于遗传算法智能改进优化蚁群算法

◆宋杨

（徐州生物工程职业技术学院 江苏 221006）

作为进化模拟新算法之一，蚁群算法旨在找寻最短路径。但蚁群算法存在一定的缺陷，如停滞、收敛慢等。所以，以遗传运算为基础，提出了一种改进后的蚁群算法，通过路径交叉与变异运算，更新了信息素，很好地优化全局、避免停滞等。基于此，本文从遗传算法出发，主要探讨了蚁群算法的智能改进与优化，仅供参考。

蚁群算法；智能优化；遗传算法

遗传和蚁群这两种算法均是启发类型的算法，且均用于最优组合求解上。但是，这两种算法均有一定的缺陷：通过遗传算法，无法发挥反馈信息的作用，会引起冗余迭代、缓慢求解等问题；通过蚁群算法，则匮乏最初信息素，会减缓算法速度。但以遗传算法为基础，适当改进蚂蚁算法，便能充分利用两种算法各自的优点，完全突破他们的缺陷，达到优势互补的效果。现阶段，在蚁群算法的基础上，优化完善遗传算法已经获得了很理想的效果。

1 蚁群基本算法概述

1.1 算法原理

在蚁群算法中，基本原理就是：在行进途中，蚂蚁会释放信息素，如果蚂蚁沿这样的轨迹前进，就能明显感觉到该激素。通过信息素，可以吸引蚂蚁前进。所以，蚂蚁往往会选择跟随信息素更浓的途径，而产生内在的催化反应，又或加强自己的正反馈效果。经由数量庞大的蚂蚁集体，而形成的行为便体现了正反馈信息现象。而通过这样的行为，蚁群就能准确找到到达目标位置的最理想的途径。

1.2 转移规则

在蚂蚁行进中，常常会根据某种转移规则。基于转移概率函数Pij，可以模拟蚂蚁选择的边（i，j）。在这个函数中，融入了信息素tij浓度、启发函数hij。针对第i点位置的第k只蚂蚁，当j不属于tabuk时，则选j的概率计算方法就是

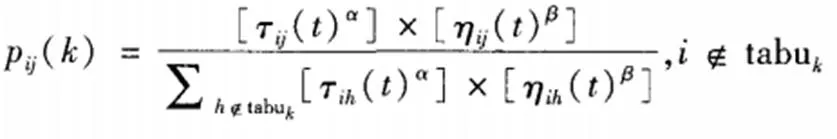
在其他时候，pij（k）=0。而tij（t）—t时刻边（i，j）对应的信息素浓度，属于全局信息，体现出蚁群的先验路段经验；hij——启发函数，通过源问题下的贪婪算法获得，仅思考本地信息，体现蚂蚁运动中出现的诸如长度等启发信息；α、ß—信息素基础下的启发、能见度因子；tabuk—第k只蚂蚁集合发不可行节点。比如，从TSP问题上看，已经过路线上的点，便为不可行类型的点。

1.3 更新信息素

根据转移规则，蚂蚁会沿各种节点向前行进，一直到形成源问题的一个处理方案。譬如，针对TSP问题的一个有效解决方案，便为蚂蚁找出一条可以遍历一切点的准确线路。而当蚂蚁得出解决方案后，就是蚁群算法基础下的一次循环。当循环一次后，就会根据更新策略，再次更新各边信息素整体浓度。

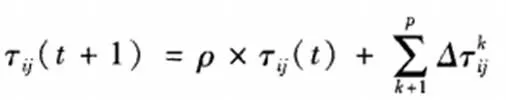
式中，ρ—残留信息素系数（0，1）；Dtijk—当前循环中第k只蚂蚁边（i，J）上出现的增量；p—整体上的蚁群规模，常见更新策略：Ant—quantity；Ant—density； Ant—cycle。其中的区别就是信息素更新方式。在前两种模型中，蚂蚁均不是在终结路径后才开始释放信息素，也就是使用局部信息，而在最后一个模型中，用到了整体信息。

最初在不同城市放m只蚂蚁，控制各边信息素具有一样的浓度，即tij（0）=C。各蚂蚁tabuk首个元素初始值就是其节点。在蚂蚁均搜索完一次后，算出tijk，再更新各边信息素实际浓度，即进入下一个循环。如果循环预定次数，又或蚂蚁均选择某路径，就应终止所有算法。

2 交叉智能优化变异改进

和别的优化算法相同的是，蚁群算法和容易出现局部最优情况。因此，应添入交叉、变异后的算子，令蚂蚁基础算法在出现局部最优并且停滞不前的情况时，丰富蚂蚁种群，以防算法过于早熟。在广阔的自然界，重组遗传基因和生物的变异，在生物进化当中发挥着核心作用。而在遗传算法中，遗传交叉算子也具有核心作用。其中的交叉指的是先替换重组2个父代个体，再产生新的个体。在交叉以后，可以大幅提升遗传算法在搜索方面的能力。作为交叉算子，可按交叉率，随机交换种群两个体的基因，并形成基因新组合，以组合有益基因。通过遗传算法变异，旨在赋予遗传算法随机搜索和丰富群体的能力。基于交叉算子，遗传算法接近到蚁群最优解邻域时，通过随机搜索，就能加速收敛至最优解。在以上情况下，无疑应取较小变异概率，不然就会因变异破坏接近最优解以后的积木块。而通过维持算法多样性，还能避免非成熟收敛，所以需取较大收敛概率。

在遗传算法当中，考虑到全局搜索，宜以交叉算子为关键性算子，以变异算子为辅助算子。从遗传算法上看，通过配合交叉、变异，能兼顾均衡搜索全局、局部的能力。这里说的彼此配合指的就是在群体进化中，无法凭借交叉，摆脱搜索空间当中陷入的某超平面时，借助变异操作，便能帮助摆脱。而彼此竞争指的就是在交叉过程中形成积木块时，而在变异操作下，却常常会破坏掉积木块。所以，在遗传算法中，应注意有机配合交叉与变异操作。

在算法当中，赋予了蚂蚁一定的粒子性，并有参考粒子群算法理论：针对粒子而言，适应值均由优化函数直接决定，并且还存在一个速度，来直接决定粒子的飞翔距离及方向，这样粒子群便会随着最优粒子不断搜索解空间。作为粒子群，常用优化算法时，先初始化形成随机粒子群，再基于迭代寻找最优解。每次粒子进行迭代时，都会跟踪2个极值来统一进行自我更新。其中一个就是个体pbest极值，而另一个则是种群寻找出的gbest最优解。针对TSP问题，具体位置就是路径，需根据遗传算法来采取交叉变异措施：

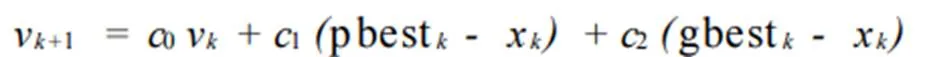
其中，c0vk—遗传算法基础下的变异；后面两项相加，可视为遗传算法基础下的交叉，也即蚂蚁均交叉运算了当前解和全局及个体极值，而得到的解就是新位置，再按新位置，算出最终的最短路径。

通过变异，经由c0路径变异至c1路径，从1～n个城市中，选取访问j1次后的城市，并在c0中直接交换访问第j1~第j1+1次的城市，再维持其他不变，就形成c1路径。例如，c0=1~9，j1=3，可得c1=12435~9。通过交叉，在第2串中选择某交叉区域，再在一定的old1位置，添加old2交叉区，并删掉old2交叉区已有的old1城市。譬如，有父串old1=1~9，old2=9~1，当交叉区是7654，可得new1=127~389。

针对TSP问题，具体算法步骤：

（1）初始化

针对随机出现的m个初始解，设置有S个初始解途径（i，j）路径，且总长L1，L2~Ls，可得初始路径信息量：

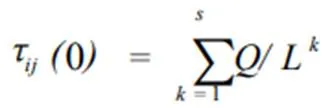
（2）迭代

While not结束的do条件；

For j对n个城市展开循环，也即为1 to n do；

for k对m只蚂蚁展开循环，也即1 to m do。

按所处位置算出不同路径长，以ptbest个体极值为适应值，以pcbest个体极值为当前位置，按粒子个体极值，寻找ptbest全局极值及其gcbest位置。在当前解集，放置每蚂蚁初始点，并根据pijk，移动蚂蚁k（k=1~m）到下个城市j，并在当前解集纳入顶点。针对蚂蚁展开这样的操作：交叉C0（j）和gcbest，获得C′1（j），再交叉C′1（j）和pcbest，获得C″1（j），然后C″1（j）基于某概率变异，获得C1（j）。按当前位置算保护路径长，如果目标新函数得到优化，就纳入新值，不然就应拒绝。C1（j）也即C0（j），再次寻找个体极值ptbest与pcbest位置，以及全局极值gtbest与gcbest位置。算出蚂蚁总路径长Lk（k=1~m），记下最佳解。针对Lk在给定值以下的路径，适当更新信息素结果。

从m只蚂蚁出发，终止循环，也即end for k；

在这m只蚂蚁当中，如果存在当前已经遍历路径长、已超出上次迭代最优路径长，就要终止本次该蚂蚁的遍历迭代。

从n个城市出发，终止循环，也即end for j；

针对各城市路径，更新总的信息量；

完成算法，获得最终解，也即end while。

3 结论分析

在实验当中，以50个城市为问题对象，依次通过蚁群算法、新提出算法来统一运算。已知α、β为1、5，增强信息素系数Q=100，挥发信息素系数ρ=0.95。一共有50只蚂蚁，迭代次数最多200次，在一台机器上，先同等设置参数，再计算这些城市问题。结果显示，新算法既有强大的搜索能力，又能更快接近最优解，还能在得到最优解后，继续稳定在其附近。由此可见，新算法在TSP的对称、非对称问题上，均能有效收敛，算出城市最终路径。

在分析实验数据信息后，根据蚁群算法，算出路径最短值457.5103，而根据优化后的新算法，得到最终解475.3594，要大于蚁群算法得到的结果。这说明新算法具有一定的优势，如有效防止早熟、出现局部收敛等，尤其适合解决大型TSP问题。在新算法应用当中，蚂蚁可以从上次迭代出发，动态地更新信息量。相较于传统算法下常用的搜索机制，尤其是蚁群基础算法下的搜索，不再会由于只是更新最优行驶路径产生的信息量，而太过强化其中的最优信息。这么一来，蚂蚁便能在搜索时“随机应变”，令大多数蚂蚁搜索，可以进化到适应度更强的方向。所以，改进后的新算法可以动态平衡收敛速率与避免早熟措施，整体上的最优解探索能力更强、进化速度更快。

4 结语

综上所述，以遗传算法为基础，通过智能化地优化改进蚁群算法后，能够更适合解决多目标大规模优化问题，并且很好地克服权重系数方面的缺陷。经过改进后的新算法，可以利用遗传算法来初始分布信息素，并且发挥出蚁群算法的优势，来提高求解效率，迅速获得多目标优化的最优解，从而增强蚁群新算法的稳定性、收敛性，赋予解更强的丰富多样性，妥善处理各种优化问题。

[1]秦浩森，丁咚，王祥东，李广雪，权永峥.蚁群算法优化BP神经网络声学底质分类方法[J].中国海洋大学学报（自然科学版），2019，49（S2）：60-68.

[2]金超迪.基于改进蚁群算法的无线传感网分簇与路径规划[D].南京邮电大学，2017.

[3]邱莉莉.基于改进蚁群算法的机器人路径规划[D].东华大学，2015.