110kV 输电线路树木临近时电场变化规律与临界击穿距离研究∗

赵海龙 黄 松

（海南电网有限责任公司电力科学研究院 海口 570100）

1 引言

输电线路树木闪络引起的跳闸故障近年来已成为电网关注的一个焦点问题，尽管其发生频度低于雷击以及外破等典型故障，但树障发生后线路重合闸难以成功，极容易造成线路停运，国内外已发生了多起因树障而导致的电网大停电事故［1～2］。

树木中富含高电导率水分，此外，树木顶端边缘曲率半径较小，具有较为尖锐的尖端。当树木临近输电导线后，树木顶部容易产生电晕放电现象，使得树木烧伤，一方面损伤树木，另一方面也容易引起火灾［3～4］。当树木临近输电导线时，树木顶端电场畸变，超过了临界击穿场强后即形成放电现象。深入研究树木临近输电导线过程中电场及电位分布变化特性，对于理解输电线路树木故障形成机理、计算最小净空距离以及指导线路走廊内树木管理具有较好的工程指导意义［5～7］。

目前相关的研究多针对特高压直流输电线路树木临近时电场计算相关问题，暂无交流场下树木存在时电场变化规律研究［9～11］。交流线路下树木临近时计算模型与原理跟线路下方人体、建筑等存在情况类似，可通过有限元法进行分析与研究［13～15］。本文使用ANSFOT 电磁场仿真软件搭建了输电线路下方树木存在时三维仿真模型，分析了树木沿不同方向临近时电场变化规律及分布特性，对垂直方向以及水平方向路径电场特性规律进行了计算。

2 树木电导率和介电常数对建模的影响

活性树木富含水分，具有一定的导电特性，但树木不是良导体，在电场作用下会产生电荷极化效应。在计算树木临近输电导线过程中电场变化特性时，需考虑树木的介电常数与电导率对电场分布的影响［16］。

如图1（a）所示，E 为一均匀工频电场，在该电场里放置了一相对介电常数为εr、电导率为γ 的薄片。在外电场作用下，薄片中的自由电荷将向表面移动，并在表面产生一定的电荷密度σ 。与此同时，薄片材料中的偶极子在电场作用下发生计划，并在表面产生极化电荷密度σ′。

图1 薄片材料自由电荷示意图

忽略边缘效应，利用高斯定理可求出自由电荷密度 σ 产生的电场［17］：

由于E1与原工频电场E 方向相反，因此作用在薄片材料上的电场E2大小为

在E2作用下，材料内部发生极化，导致内部电场降低，降低程度与材料相对介电常数相关。考虑材料实际相对介电常数后，材料内部的电场强度则为

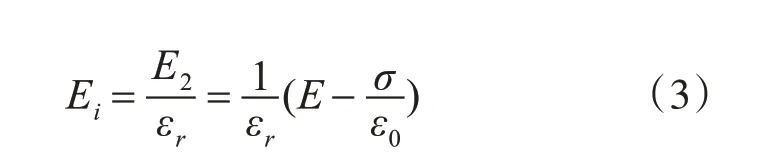
根据文献［7］，在交变电场作用下，电场强度与自由电荷密度有如下关系：

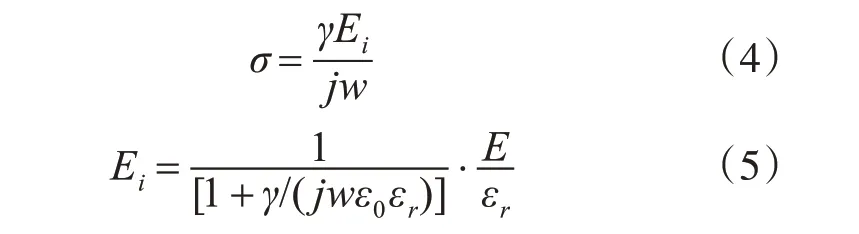
活性树木材料电导率一般为1e-3～1e-1S/m，相对介电常数为2～10 之间［18］。在工频电场作用下，γ/wε0εr≫1，此时式（5）可简化为

式中，J 为传导电流密度。此时树木材料传导特性与金属相同，因此在计算树木临近输电导线电场变化特性时，将树木材料定义为良导体，且树木电位保持为0。

3 模型建立

树木包含大量的树叶以及枝干，其结构及其复杂，建模时需要加以简化。此外，树木种类以及形状各异，为简化分析，选取几类常见的树木进行分析。图2 所示的几种树木树冠依次为椭球体、圆锥体、球体，仿真时用标准的几何体进行等效。由于树木下端枝干结构对电场分布影响相对较小，树木枝干统一用圆柱体进行模拟。

图2 三种常见形状的树木

图3 树木三维简化仿真模型

由于导线具有一定的弧垂，因此档距中央导线离地高度最小，相对来说更容易发生树木闪络故障。模型中仅考虑树木在档距中央附近时电位与电场分布特性，此时树木与杆塔距离较远，一般超过100m，杆塔的存在对树木附近电场影响不大，为简化分析，忽略杆塔的影响。此外忽略金具、防震锤、绝缘子等对树木临近时电场分布影响较小的部件，可大幅简化计算量。

考虑良好的导电性，避雷线、导线、树木、接地极材料均设置为铝。接地极用一400m*40m*0.05m的金属薄板模拟。导线型号为LGJ-185，其外径为19mm，模型中分别用等粗圆柱体棒模拟导线及避雷线。避雷线、导线布置情况以及考察路径示意图如图4 所示。图4 中考察路径有两条，其中竖直路径（简称路径1，下同）为树木正上方长度为5m 的直线段，且线段距离边相导线1m 保持不变。水平路径（简称路径2，下同）则为档距中央B 相导线下方4m处水平向外5m的直线段。

图4 避雷线、导线布置情况以及考察路径示意图

4 仿真结果与分析

4.1 电场及电位分布特性

A、B、C 相 导 线 施 加 电 压 分 别 为-44.9kV、89.8kV、-44.9kV。树木位于档距中央B 相导线正下方，且与导线最小垂直距离7m，不同树木存在时空间电场及电位分布特性分别如图5所示。

从图5（a）、图5（b）可以看出，由于模型的对称性，空间电场及电位分布呈现出左右对称规律。此外，树木的存在使得树木附近空间电场及电位分布发生了较为明显的畸变，不同树冠下的空间电场分布存在差异，其中圆锥体树冠表面附近电场畸变程度最大，其最大场强超过3.6kV/cm，而球体树冠及椭球体树冠表面最大场强依次为1.4kV/cm 和1.9kV/cm。

图5（c）中Li为路径1上被考察点距路径1起始点的距离。图5（c）中，球体树冠模型与椭球体树冠模型下路径1 电场分布较为一致。由于树木均与导线距离较远，因此路径1 沿线电场强度较低，均低于2.5kV/m。图5（d）中Lj路径2 上被考察点距路径2起始点的距离，在起始位置由于A、B、C三相电源正负叠加作用，使得场强较低，沿路径2 往外，随着距离增加，场强呈先增加后减小趋势，最大场强出现在Lj=3.4m处，此时正处于边相导线正下方。

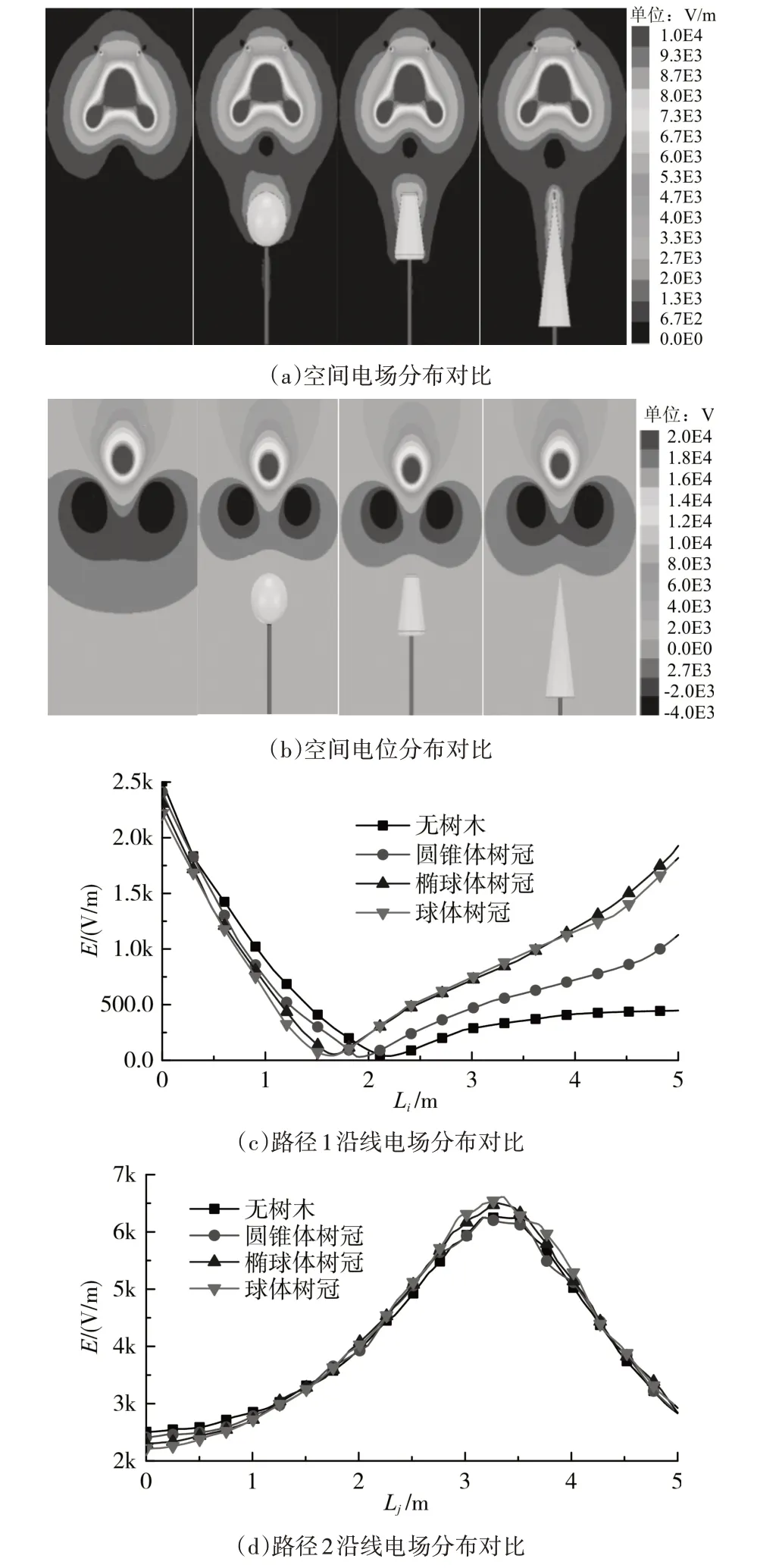
图5 不同种类树木存在时空间电场及电位计算结果对比

4.2 树木高度对计算结果的影响

圆锥体树冠对空间电场畸变影响较大，以圆锥体树冠为例，分析树木高度对电场分布的影响。让树木正对导线，逐渐减小树木与导线垂直距离，模拟自然界树木逐渐长高过程。改变树木高度H，当树木与B 相导线距离取7m、6m、5m、4m 时，被考察路径沿线电场分布对比如图6所示。

图6（a）中，对于4m、5m 以及6m 三种情况，由于树木高度较高，路径1 的下段一部分在树冠内部，由于树冠为良导体，内部场强为0，对应曲线电场为0 的一部分。从曲线变化规律来看，随着树木的不断长高，路径1 沿线电场分布呈上升趋势，越靠近树冠顶部，场强畸变越明显，7m、6m以及5m三种情况下最大场强依次为13.2kV/m、12.1kV/m、9.3kV/m。路径2 由于靠近导线，且离树木距离较大，树木高度变化对路径2 上电场分布影响相对较小。

图6 不同树木高度下考察路径沿线电场分布

4.3 树木水平距离对计算结果的影响

改变树木与输电导线水平距离s，仿真结果如图7所示。

图7 中，0m 为导线正下方，从图7（a）中看出，随着水平距离增大，路径1 场强整体呈减小趋势。对比水平距离1m 和0m 两种情况，其中1m 对应曲线最大场强为11.2kV/m，高于0m 下9.8kV/m，这是因为水平距离为0 时，树木正对着边相导线，由于中相导线激励源与边相相反，导致边相导线正下方场强出现了明显的削弱，距离较远时这种叠加效应不明显，因此水平距离1m 时最大场强超过0m 情况，但整体电场分布低于0m 时的电场分布。图7（b）分布曲线对比表明，树木离导线水平距离的变化对导线下方水平路径的电场分布影响不大，与4.2规律类似。

图7 不同水平距离下考察路径沿线电场分布

4.4 树木数量对仿真结果的影响

输电线路走廊内树木种类、数量以及分布均是随机因素，仿真中树木数量N 依次取1、3、5、9 几种情况，树木分布如图8 所示。导线均正对树木，树木与树木之间轴线距离均为6m。仿真结果如图9。

图9 不同水平距离下考察路径沿线电场分布

从图9 看出，树木数量对路径1 和路径2 电场分布影响不大，最大场强差异保持在10%以内，表明临近树木对被考察树木附近区域电场分布影响规律较小，计算时可忽略树木数量的影响。

4.5 临界击穿距离的确定

树木-导线间隙为稍不均匀场或极不均匀场，其放电击穿过程属于工频电压作用下长空气间隙放电范畴［16，18］。间隙击穿为极其复杂的动态过程，并伴随声、光、电热效应，目前尚无有效模型精确模拟放电过程［13～15］。流注放电是长空气间隙放电的重要阶段，其起始特性可以作为间隙击穿特性的重要参考，已有较多文献对流注起始特性进行了研究，并提出了不同的流注起始判据，本文采用文献［16］提出的典型极不均匀场棒-板间隙流注起始判据：

式中，Ei-impulse为流注起始场强，kV/cm；R 为电极平均半径，本文锥形树冠平均半径取2.5m；dU/dt为施加电压变化率，单位kV/μs。

在工频电压作用下，有

将R=2.5m 代入式（9），可计算出流注起始场强为39.6kV/cm。当树冠顶部合成场强达到该值时，为临界击穿状态，此时树木高度为临界树木高度，树木与导线距离dlj则为临界击穿距离。

改变树木高度与树木-导线水平距离，通过ANSFOT 仿真软件计算临界击穿距离流程如图10所示。

图10 临界树木高度计算流程

图10 中，α0为电源相角，s'为最大水平位移，ΔH 为高度增量，Δs 为水平距离增量，根据实际线路布置情况，取ΔH =0.1m，Δs=0.2m。

按图10 所示流程确定临界击穿距离过程如下：首先通过初步仿真，判断在相角α0，初始树木高度H0，初始水平距离s0下，逐渐增加水平距离至最大值s'过程中，均未出现树冠顶部场强达到流注起始场强的情况，将此时H0、s0作为仿真初始条件，然后将树木高度增加ΔH ，依次按步长Δs 改变水平距离，并在不同的水平距离下判断树木顶部场强，若达到流住起始场强，此时对应的树木高度即为当前施加电压下的临界树木高度，反之，则继续增加树木高度，并重复上述过程。计算出临界树木高度后，通过几何法即可确定临界击穿距离。根据上述计算流程，计算了不同电源相角下临界击穿距离，结果如表1所示。

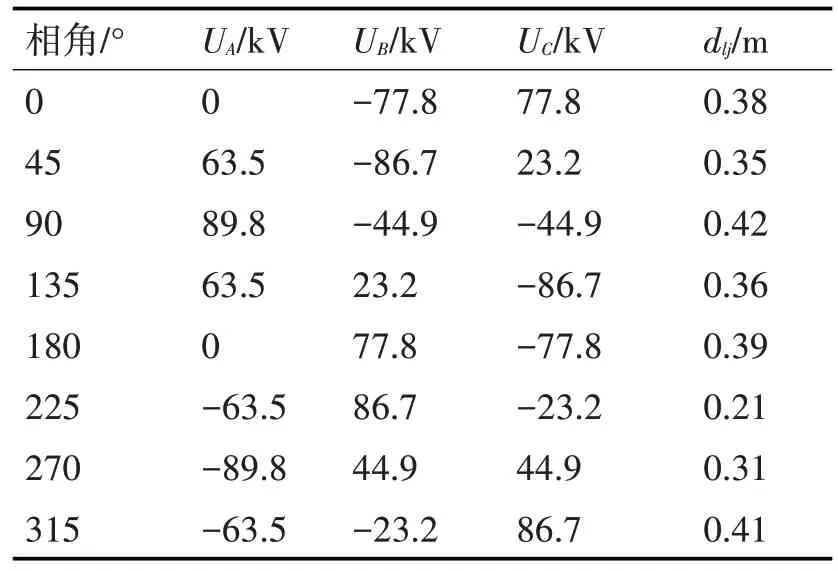
表1 不同电源相角下临界击穿距离计算结果

表1 数据表明，不同电源相角下，临界击穿距离存在差异，当边相电压瞬时值处于正极性峰值时，树木距导线距离达到0.42m 时树冠顶部即产生流注放电，而在特定相角下，为使达到流注起始场强条件，树木与导线距离需达到0.21m 范围以内。由于放电存在分散性，并且放电受环境、树木本体状态的影响，树木-导线放电可能发生在电源的任意一相角下，为保留足够的安全裕度，树木-导线临界击穿距离应取最大值0.42m，即，实际工程应用中，对于图4 所示110kV 输电线路来说，应尽量避免树木过于临近输电导线，极限距离不应低于0.42m，否则容易造成树木闪络故障的发生。

5 结语

1）在工频电场作用下，树木传导特性与金属类似，可以用良导体来模拟树木对工频电场分布的影响；

2）随着树木高度增加以及树木与输电导线水平距离的逐渐临近，空间电场分布逐渐增大；具有较尖顶部树木对空间电场影响更为明显，更容易引起电场畸变并导致闪络发生；

3）对于本文示例线路，树木与导线距离达到0.42m 时树木顶部场强超过流注起始场强，容易形成树木闪络故障，因此为避免故障发生，树木与导线距离需大于0.42m。