基于无刷直流电机的皮带传送系统设计及仿真∗

吴建波 朱凌云 陈光琛 韩 雪

（东华大学信息科学与技术学院 上海 201620）

1 引言

为了设计出适用于纽扣在线视觉检测的皮带传送系统，要求控制皮带运转的电机转速十分平稳，不能有抖动。本文选用无刷直流电机对皮带传送系统负载进行建模与仿真，利用该模型得到了带负载时电机运行的转速、转矩、相电流、反电动势和PWM 曲线，仿真结果与理论分析一致，验证了该模型建立的可靠性和准确性。

2 皮带传送系统的分析与设计

皮带传动的原理是靠摩擦传动，主要掌握如何靠带与带轮之间的摩擦力来传递动力。为了使分析问题简化，研究主动轮各点上的传送带张力时，可以认为传送带是理想的挠性体，可以任意弯曲，不受弯曲应力［1］。

2.1 皮带传送系统的力学分析

在皮带传送过程中，传送带需以一定的初张力F0紧套在两个带轮上。如图1 所示，传送带工作时，设主动轮以转速n1转动，由于传送带和带轮接触面上的摩擦力的作用，使从动轮以转速n2转动。这时，传送带两边的拉力也发生相应的变化：传送带进入主动轮的一边被拉紧，称为紧边，拉力由F0增加到F1；传送带进入从动轮的一边被放松，称为松边，拉力由减小到F2［2］。

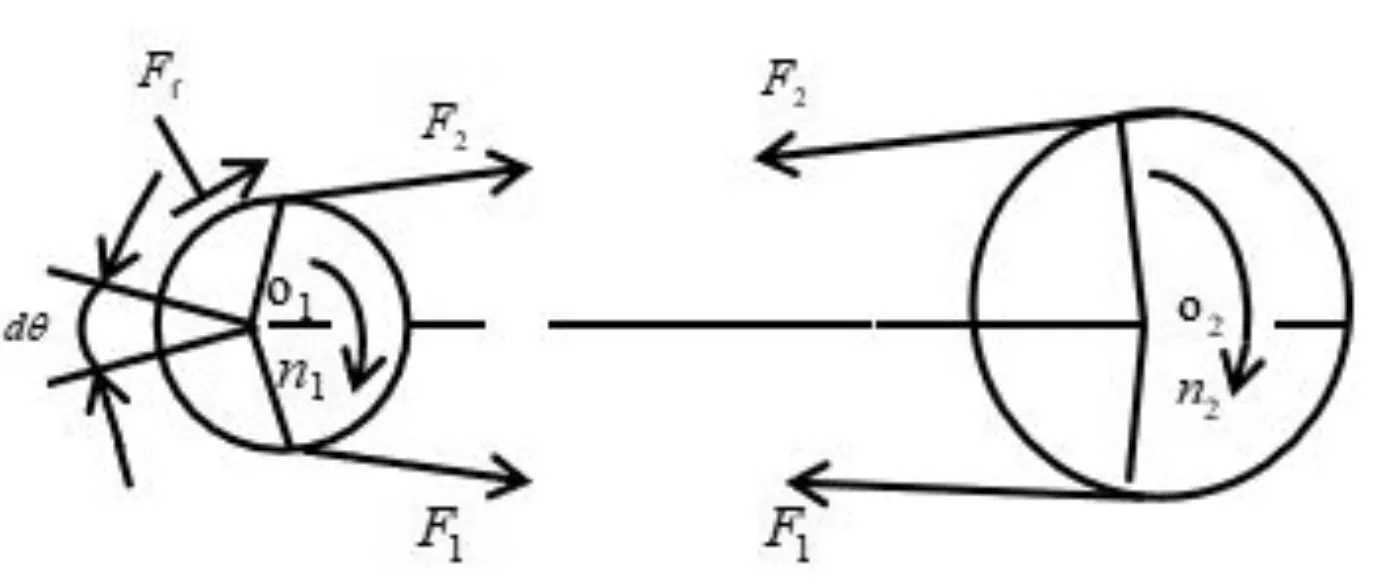
图1 带传动的受力分析

根据作用在传送带上的总摩擦力Ff以及紧边拉力F1和松边拉力F2对轴心O1的力矩平衡条件，可得

传送带紧边与松边的拉力之差就是传送带的有效拉力Fe，即

显然，Fe=Ff，在主动轮轮缘上截取的微段长度传送带为分离体，则

联立上式，可得皮带传送的紧边拉力、松边拉力以及有效拉力的关系为

2.2 皮带传送系统的几何分析

如图2 所示，皮带传送系统的基本几何参数主要包括带轮准直径d1,d2，小带轮上的包角α1，基准带长L和中心距a。

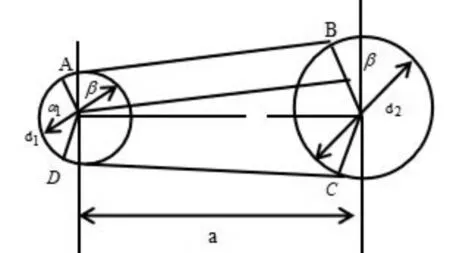
图2 带传动的几何关系

2.2.1 包角α

传送带与带轮接触弧所对应的中心角称为包角，由图2可知，小带轮上的包角为

2.3 皮带传送系统的设计计算

针对机器视觉检测系统的要求，设计适用于纽扣运输生产线的皮带传送系统，要求皮带能够匀速、稳定的运行，不出现皮带打滑现象。根据实际要求设计皮带的运行速度为v=2.0m/s，按照皮带轮的标准直径选择主动轮直径d1=125mm ，从动轮直径为d2=140mm，中心距a=2000mm采用开式传动，定期张紧，选用环形平带，传动接近水平。

2.3.1 主动轮转速

根据公式：

上述计算中μ 为带轮和传送带的摩擦系数，带轮材料为铸铁，μ 取0.5。

2.3.8 力矩计算

由上述式（9）计算出主动轮的转速n1=306r/min ，选 用 的 带 轮 为C 型4 槽 ，重 量m=4kg ，直 径d1=125mm ，主 动 轮 转 速 从0 到n1=306r/min 所用时间t=0.1s。

2.3.9 无刷直流电机选型

由以上计算可知所需功率P1=0.468kW，力矩M=0.398N ⋅m，主动轮转速n1=306r/min。

由于纽扣运输生产线的皮带传送系统是转速比较低的设备，所以需要采用减速器，具有降低转速、传递动力、增大转矩的作用。本文减速比i=5∶1。表1为本文无刷直流电机相关参数。

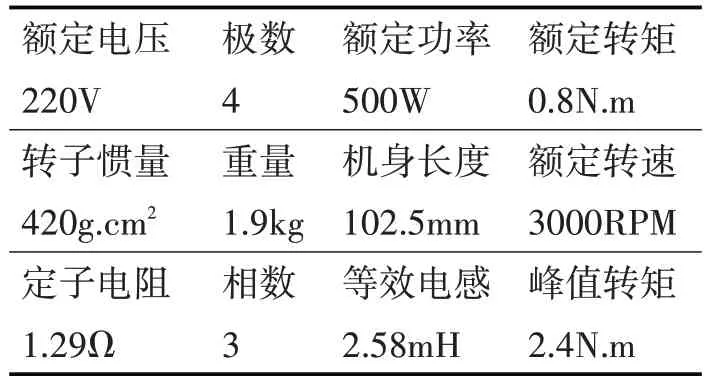
表1 无刷直流电机参数

3 BLDCM的数学模型

本文以三相六状态两两导通的星型连接的无刷直流电机为例，转子的磁阻不随转子位置变化而变化［3～5］。为了便于分析，作以下假设：

1）转子永磁体产生的气隙磁场为方波，三相绕组反电动势为梯形波；

2）忽略定子绕组电枢反应的影响；

3）电机气隙磁导均匀，磁路不饱和，不计涡流损耗；

4）定子齿槽的影响忽略不计；

5）三相绕组电阻、电感、互感参数完全相同。

3.1 BLDCM的电压平衡方程

对于三相无刷直流电机，其电压平衡方程可表示为［6～7］

式中：Ua,Ub,Uc为定子每相绕组相电压（V）；Ra,Rb,Rc为定子每相绕组电阻（Ω）；ia,ib,ic为定子每相绕组相电流（A）；La,Lb,Lc为定子每相绕组自感（H）；Lab,Lac,Lba,Lbc,Lca,Lcb为定子每两相绕组间的互感（H）；P 为微分算子(P=d/dt)；Ea,Eb,Ec为定子每相绕组反电动势（V）。

根据上述假设三相绕组电阻、电感、互感参数完全相同，则令Ra=Rb=Rc=R ，La=Lb=Lc=L,Lab=Lac=Lba=Lbc=Lca=Lcb=M,并且三相绕组为星形连接且没有中线引出，则有：

由式（17）和式（18）可得：

根据简化的电压方程（19）得到无刷直流电机的等效电路图，如图3所示。

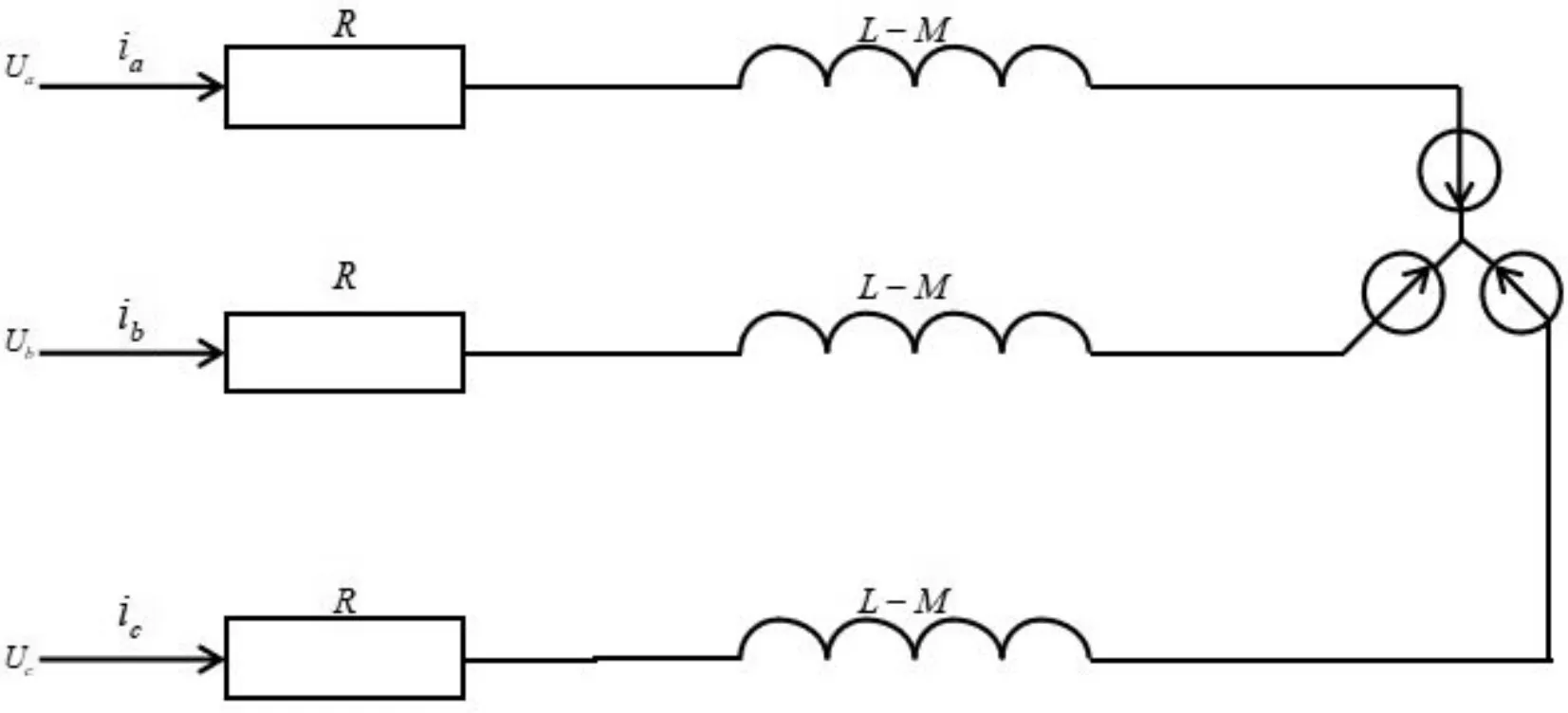
图3 无刷直流电机等效电路图

3.2 BLDCM的电磁转矩方程

因为任意时刻电机的电磁功率是三相绕组电磁功率之和，则有：

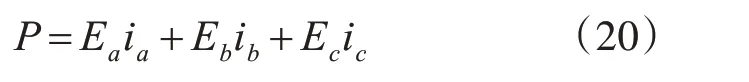
它用来驱动电机转子转动，所以在电机运行过程中，电磁转矩的表达式为

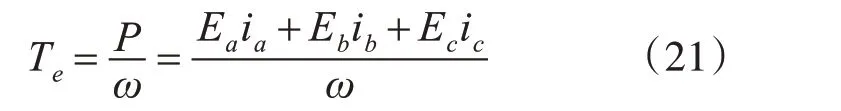
式中，Te为电磁转矩(Nm) ；ω 为转子角速度(rad/s)。

3.3 BLDCM的机械运动方程

电机的机械运动方程为：

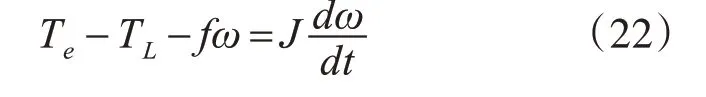
式中，Te,TL分别为电磁转矩和负载转矩(Nm)；f为阻尼系数(N ⋅m ⋅s)；ω 为转子角速度(rad/s)；J为转子的转动惯量(kg ⋅m2)。

4 BLDCM仿真模型的搭建

BLDCM 仿真模型的总体结构框图如图4 所示。其中，速度控制器采用PID 控制，电流调节是使用滞环控制来完成的［8～10］。速度控制器的输入为给定转速n_ref与电机实际反馈转速n的误差，电流环接受速度环的输出作为电流给定值，其与电流反馈的实际信号I 相减得到电流误差，作为电流调节器的输入，电流调节器的输出控制PWM 波，从而调节转速。

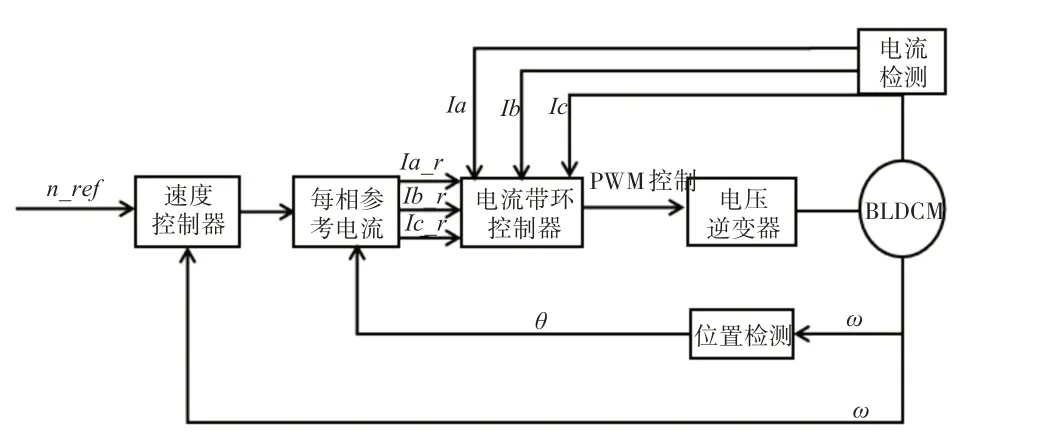
图4 无刷直流电机控制系统整体框图

4.1 BLDCM本体模块

在整个仿真模型中，BLDCM 模块是最重要的部分，该模块根据电压方程式（19）求取三相相电流，结构图及封装图如图5所示。

将电压方程式（19）化为方程组得：

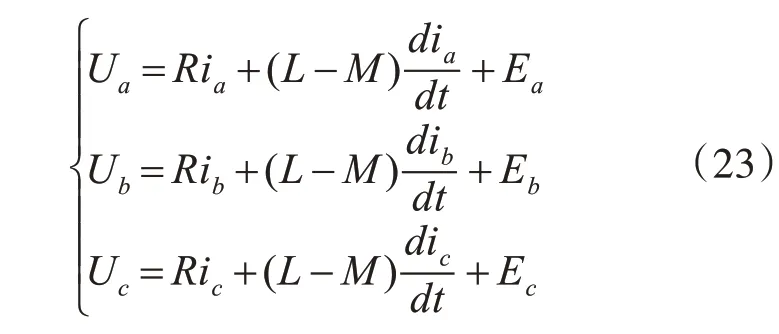
由式（23）可知，要想获得三相电流必须首先要求得三相反电动势信号。本文采用分段线性法建立梯形波反电动势波形［11］，BLDCM 理想的三相反电动势波形如图6所示。

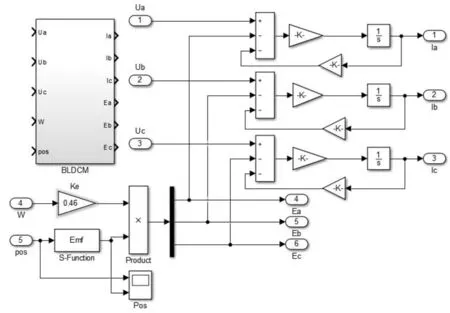
图5 无刷直流电机本体模块及其封装

图6 三相反电动势理想波形

图6 中，横坐标是电角度ωt ，纵坐标为反电动势Ea,Eb,Ec,Ke为电动势系数，三相反向电动势的波形相同，只是相位互差120°。根据角速度和转子的位置，就可以求出各相反电动势变化轨迹的直线方程。根据此规律，就可以推导出转子位置和反电势之间的关系，如表2所示。

4.2 转矩和转速计算模块

根据BLDCM 数学模型通过机械运动方程式（24），由电磁转矩、负载转矩以及阻尼系数就可以得到转速信号［12］，再通过积分可以得到电机位置信号，然后根据电磁转矩方程式（23）可以得到转矩计算模块，结构图和封装图如图7所示。

表2 转子位置和反电动势之间的线性关系表

表中，Ke为反电动势系数(V/(r ⋅min-1))，ω 为转速信号(rad/s)。

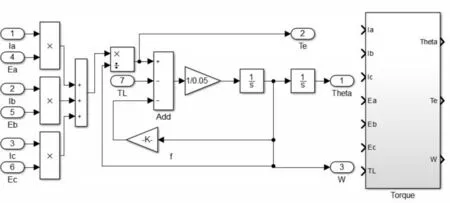
图7 转矩和转速模块及其封装

4.3 速度控制模块

转速调节器采用经典的PID 控制，参考转速n_ref和实际转速n作为输入，三相参考电流的幅值Is作为输出，并且饱和限幅模块将输出的Is限定在要求的范围之内，如图8所示。

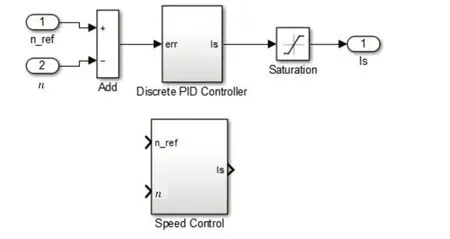
图8 速度控制模块及其封装

4.4 参考电流模块

参考电流模块的作用是根据电流幅值信号Is和位置信号Pos 给出三相参考电流，输出的三相参考电流Ia_r、Ib_r、Ic_r 作为电流滞环控制模块的输入，与实际电流比较进行控制［13～14］，转子位置和三相参考电流之间的关系如表3所示。

表3 转子位置和三相参考电流之间的关系，写S 函数来实现上表所述关系［15～16］，参考电流模块结构图和封装图如图9所示。

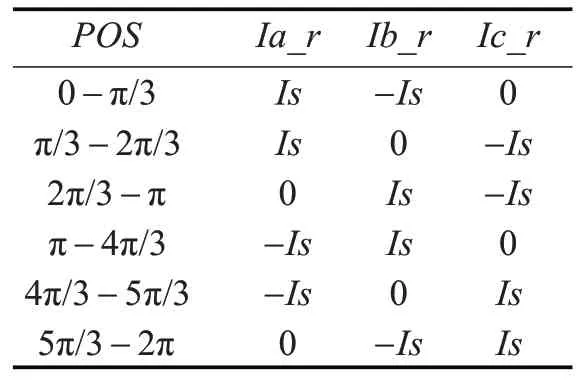
表3 转子位置和三相参考电流之间的关系

图9 参考电流模块及其封装

4.5 电流控制模块

本文采用电流滞环控制原理，目的是让实际电流不断地追踪参考电流。当实际电流与参考电流的偏差超过一定值时，改变逆变器的状态，使逆变器输出的电流减小或者增大，控制偏差在限定的范围内，其结构图和封装图如图10所示。

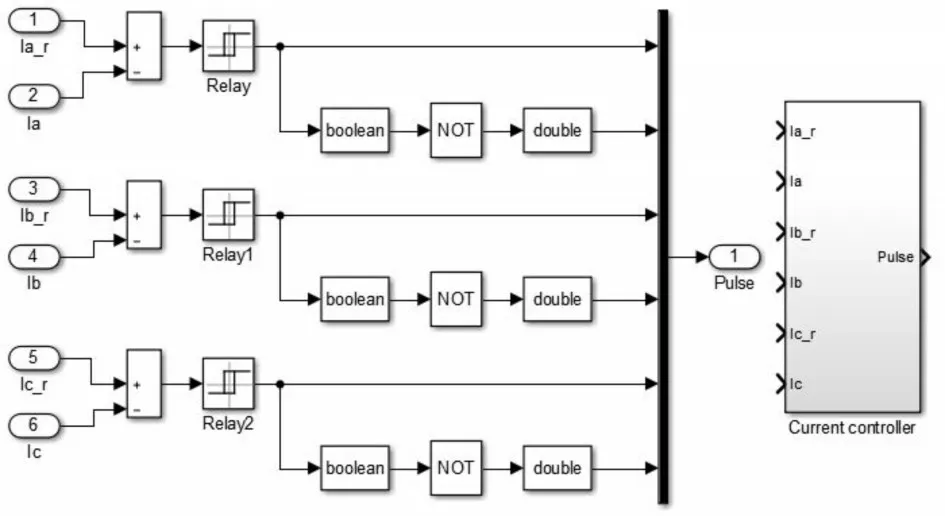
图10 电流控制模块及其封装

4.6 电压逆变器模块

在BLDCM 仿真模型中，逆变器模块具有调节PWM 的作用。模块选用三相全桥IGBT，根据电流控制模块所发出PWM 信号，按某一频率顺序导通和关断，并给出相应的三相端电压信号，其结构图和封装图如图11所示。

图11 电压逆变器模块及其封装

5 结语

本文基于无刷直流电机的皮带传送系统设计与仿真。BLDCM 仿真参数设置为：220V 直流电源供电，由于减速比i=5∶1，主动轮转速n1=306r/min，所以无刷直流电机转速设置为n=1530r/min，阻尼系数f=0.0002N·m·s，定子电阻R=1.29Ω，定子等效电感L=2.58mH，互感M=-0.061H，负载转矩为0.398N·m，转动惯量J=0.0042kg·m2。PID 三个参数 为Kp=30，Ki=0.01，Kd=0.001，采 样 周 期T=5×10-5s。BLDCM仿真模型如图12所示。

仿真参数设置如图13所示。

系统转速、转矩、三相电流、三相反电动势和PWM波形如图14～18所示。

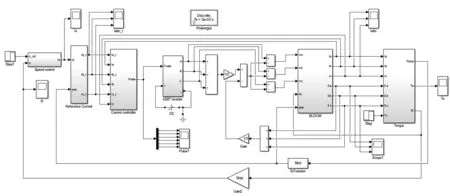
图12 无刷直流电机控制系统仿真模型

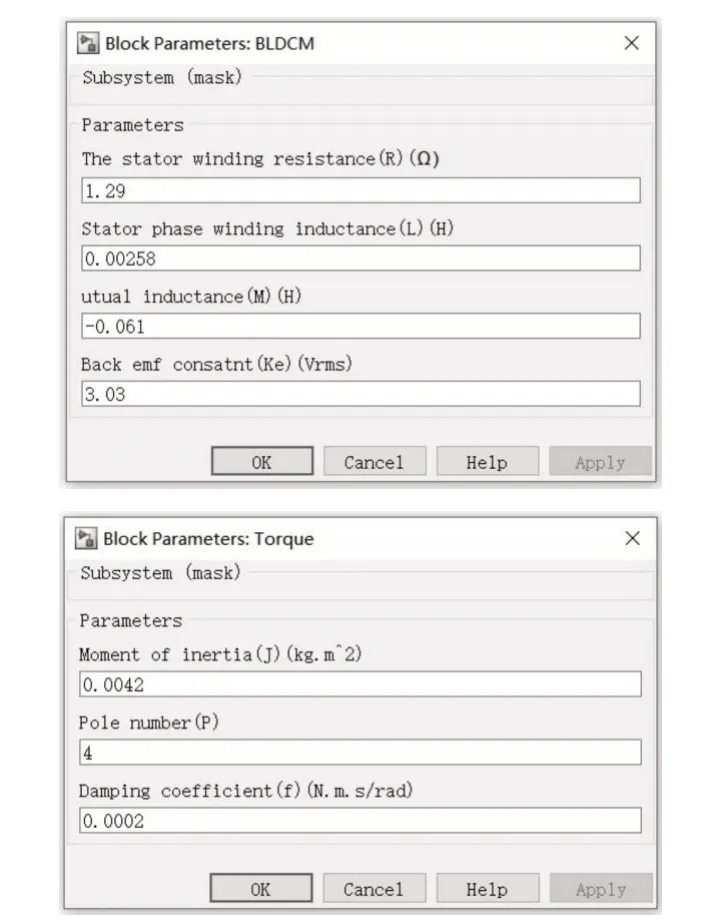
图13 仿真参数设置

图14 转速响应曲

图15 转矩响应曲线

图16 三相电流Ia、Ib、Ic 波形

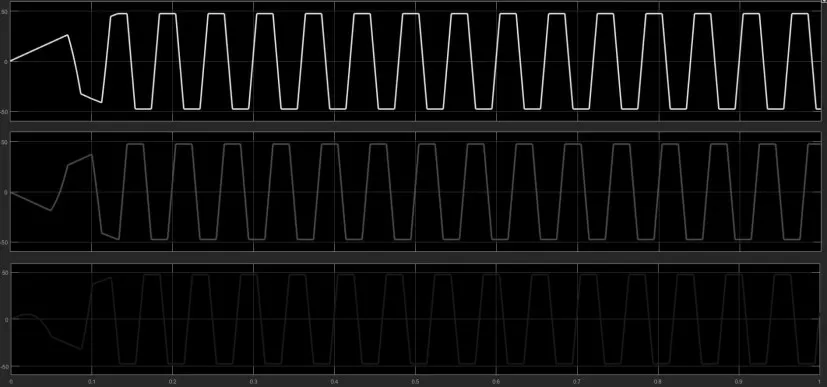
图17 三相反电动势Ea、Eb、Ec 波形

图18 PWM波形

由仿真波形可以看出，无刷直流电机带负载转矩TL=0.398N·m 在t=0.1s 时达到了n=1530r/min 的转速，系统响应速度快并且很平稳，无超调，三相相电流和反电动势波形也比较理想。验证了该模型建立的可靠性和准确性，为后面的实验提供了理论依据。