城市交通流量预测模型的研究
李劲松 易明俊

摘 要: 城市交通流量预测是具有社会价值的重要课题之一。由于城市交通流量预测涉及到一个复杂的非线性数据模式,因此精确预测的难度较大。为此,提出将支持向量回归模型(SVR)和连续蚁群优化算法(ACO)相结合对城市短期交通流量进行预测的思路。仿真结果表明,与常见的季节自回归滑动平均时间序列模型的预测方法相比,该模型能得到更准确的预测结果。
关键词: 交通流量预测; 支持向量回归; 连续蚁群优化算法
中图分类号: TP 393 文献标志码: A
Abstract: Urban traffic flow forecasting is one of the important topics of social value. Because urban traffic flow prediction involves a complex nonlinear data model, accurate prediction is difficult. To this end, this paper proposes a combination of support vector regression model (SVR) and continuous ant colony optimization algorithm(ACO)to predict urban short-term traffic flow. The simulation results show that the model can obtain more accurate prediction results than the prediction method of the common seasonal autoregressive moving average time series model.
Key words: traffic flow prediction; support vector regression; continuous ant colony optimization algorithm
0 引言
对通行能力的准确预测,会缓解交通拥挤,并在出行时间、燃料成本和环境污染等方面会产生巨大的效益,因此准确预测高峰时段的交通流量是一个非常具有社会价值的课题[1-3]。研究表明,将现有的基于模型的预测算法应用于城市公路网的交通流量预测,由于存在不同时间和不同地理位置的交通流量之间存在耦合的关联关系[4],以及交通流量建模时很难处理的流量数据噪声和缺失值[5],将出现预测结果可靠性不高的问题[6-7]。为此一些研究人员开发出季节性差分自动平滑回归(SARIMA)模型[8]应用于交通流量预测。该模型通过季节性差分自动平滑回归来考虑高峰值、非高峰值流量周期,以有效提高预测的准确性。但是,该模型在异常值检测和模型参数的训练效率方面存在明显缺陷。为此,本文提出采用支持向量机回归模型(SVR)[9-10]实现城市交通流量的预测,并采用蚁群优化算法(ACO)[11]来确定SVR模型参数。最后将所提出模型应用于武汉市公路交通流量预测,实现对其预测性能的验证。
1 预测方法
本文采用季节性差分自回归滑动平均(SARIMA)模型作为基准模型,以便对本文所设计的SVRCACO模型的预测性能进行对比。本节首先对SARIMA模型的原理进行简单说明,随后对SVR模型进行详细阐述。
1.1 SARIMA模型
在强季节性地区的交通流量预测中,SARIMA模型是时间序列预测中最常见的方法之一。SARIMA模型预测值假定为过去值和过去误差的线性组合,其常见形式为SARIMA(p,d,q)×(P,D,Q)S。其中S为季节周期的长度,d和D是非负整数。SARIMA模型的数学表达式[12]如式(1)。
由于高斯RBF核函数不仅更容易实现,而且能够将训练数据非线性地映射到无限维空间,因此本文选择高斯RBF核函数用于处理非线性关系的交通流量数据预测问题[15]。核函数高斯RBF的带宽为σ:K(xi,xj)=exp(-0.5xi-xj2/σ2),以及具有d阶和常数α1和α2的多项式核K(xi,xj)=(α1xixj+α2)d。如果σ的值非常大,则RBF内核近似使用线性内核(多项式的数量级为1)。
SVR模型的σ、ε和C三个参数的选择影响预测的准确性。由于遗传算法(GA)和模拟退火算法(SA)在知识记忆方面并没有很好的工作性能,导致搜索SVR模型的合适参数会花费大量的时间,因此本文在所提出的SVR模型中,采用连续蚁群优化(CACO)来优化参数选择。
2 SVR模型的参数优化
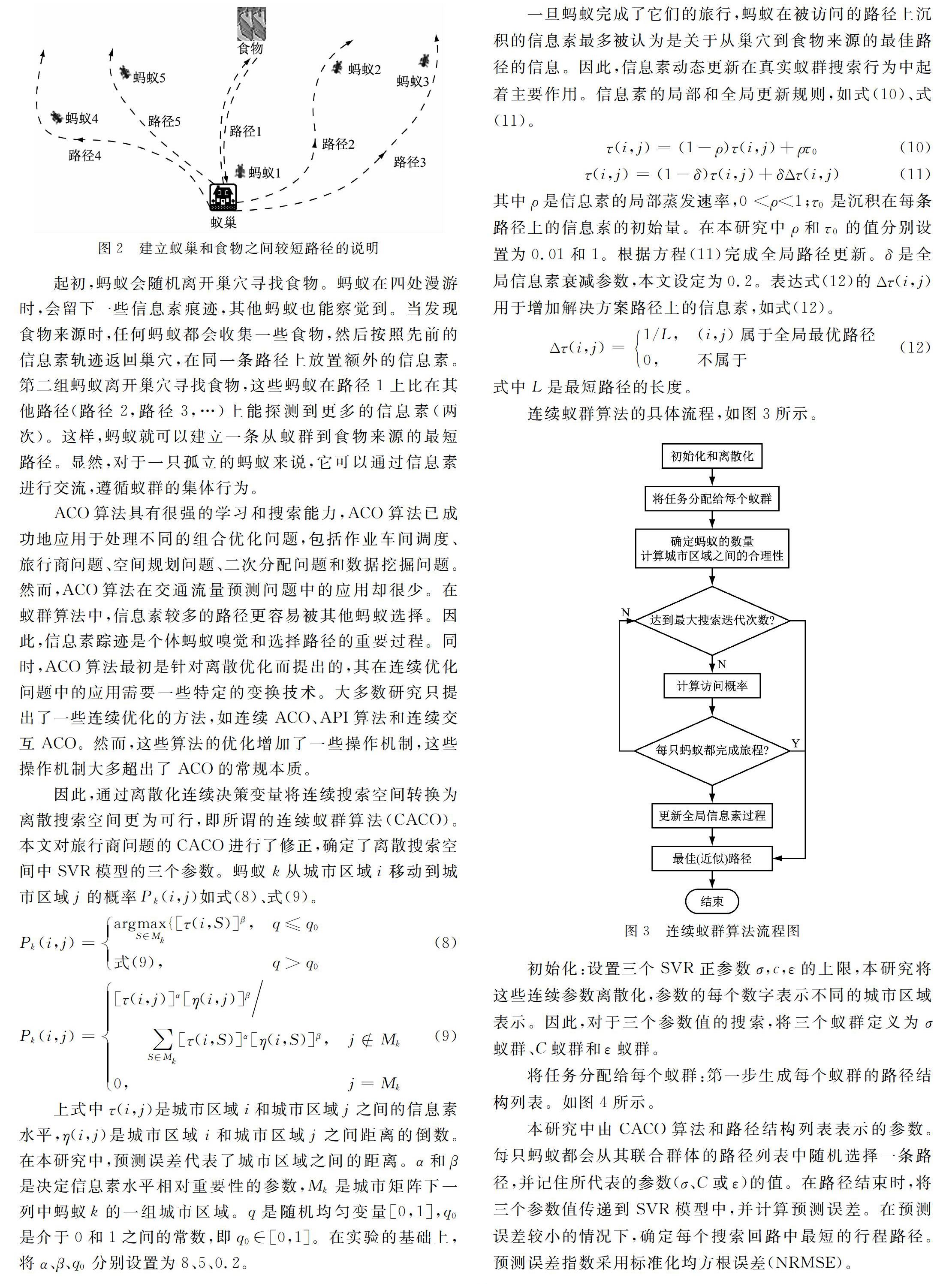
蚁群算法(ACO)的基本思路利用蚂蚁在蚁巢和食物之间建立较短路径,如图2所示。
起初,蚂蚁会随机离开巢穴寻找食物。蚂蚁在四处漫游时,会留下一些信息素痕迹,其他蚂蚁也能察觉到。当发现食物来源时,任何蚂蚁都会收集一些食物,然后按照先前的信息素轨迹返回巢穴,在同一条路径上放置额外的信息素。第二组蚂蚁离开巢穴寻找食物,这些蚂蚁在路径1上比在其他路径(路径2,路径3,…)上能探测到更多的信息素(两次)。这样,蚂蚁就可以建立一条从蚁群到食物来源的最短路径。显然,对于一只孤立的蚂蚁来说,它可以通过信息素进行交流,遵循蚁群的集体行为。
ACO算法具有很强的学习和搜索能力,ACO算法已成功地应用于处理不同的组合优化问题,包括作业车间调度、旅行商问题、空间规划问题、二次分配问题和数据挖掘问题。然而,ACO算法在交通流量预测问题中的应用却很少。在蚁群算法中,信息素较多的路径更容易被其他蚂蚁选择。因此,信息素踪迹是个体蚂蚁嗅觉和选择路径的重要过程。同时,ACO算法最初是针对离散优化而提出的,其在连续优化问题中的应用需要一些特定的变换技术。大多数研究只提出了一些连续优化的方法,如連续ACO、API算法和连续交互ACO。然而,这些算法的优化增加了一些操作机制,这些操作机制大多超出了ACO的常规本质。
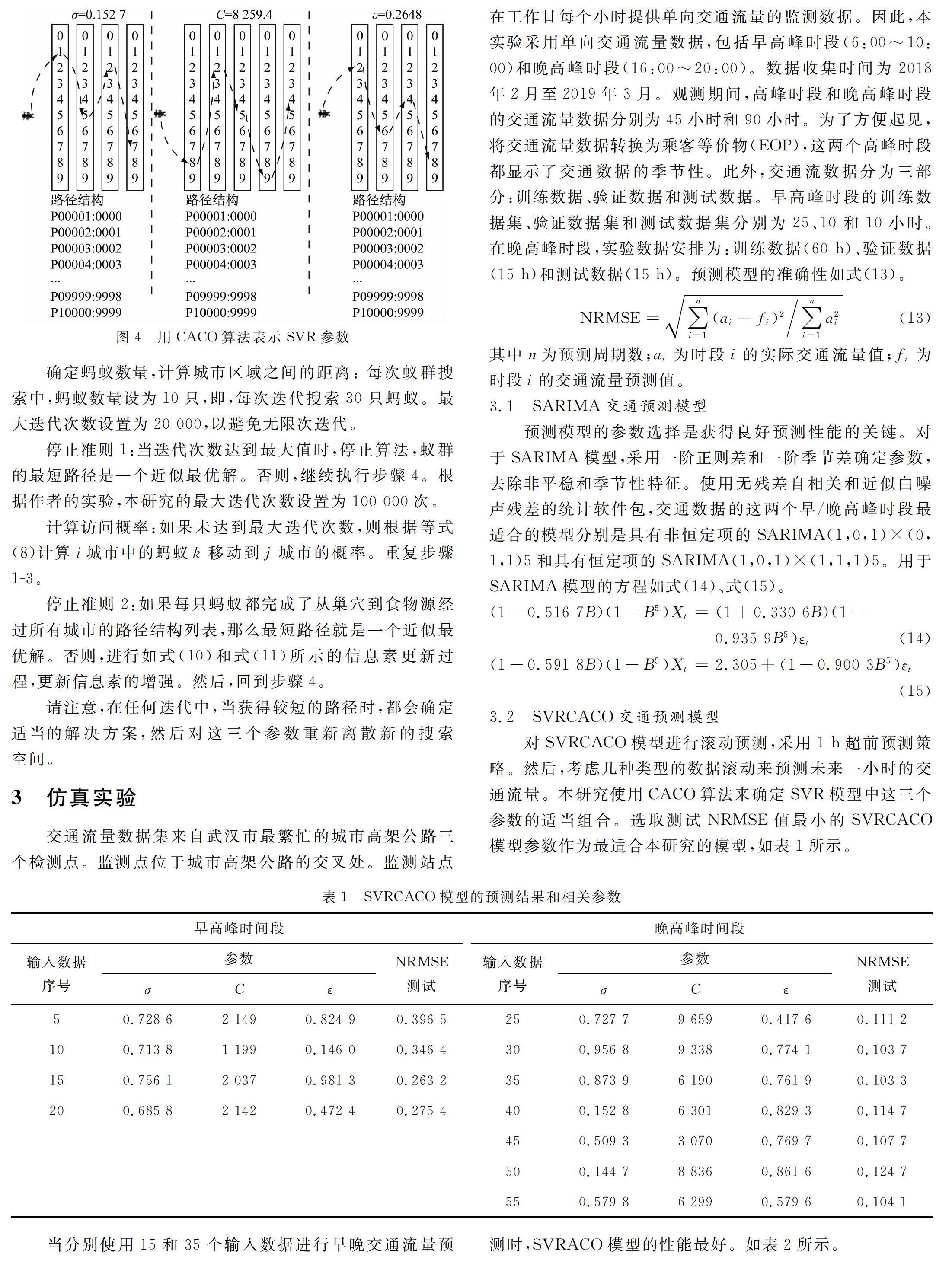
因此,通过离散化连续决策变量将连续搜索空间转换为离散搜索空间更为可行,即所谓的连续蚁群算法(CACO)。本文对旅行商问题的CACO进行了修正,确定了离散搜索空间中SVR模型的三个参数。蚂蚁k从城市区域i移动到城市区域j的概率Pk(i,j)如式(8)、式(9)。
初始化:设置三个SVR正参数σ,c,ε的上限,本研究将这些连续参数离散化,参数的每个数字表示不同的城市区域表示。因此,对于三个参数值的搜索,将三个蚁群定义为σ蚁群、C蚁群和ε蚁群。
将任务分配给每个蚁群:第一步生成每个蚁群的路径结构列表。如图4所示。
本研究中由CACO算法和路径结构列表表示的参数。每只蚂蚁都会从其联合群体的路径列表中随机选择一条路径,并记住所代表的参数(σ、C或ε)的值。在路径结束时,将三个参数值传递到SVR模型中,并计算预测误差。在预测误差较小的情况下,确定每个搜索回路中最短的行程路径。预测误差指数采用标准化均方根误差(NRMSE)。
确定蚂蚁数量,计算城市区域之间的距离: 每次蚁群搜索中,蚂蚁数量设为10只,即,每次迭代搜索30只蚂蚁。最大迭代次数设置为20 000,以避免无限次迭代。
停止准则1:当迭代次数达到最大值时,停止算法,蚁群的最短路径是一个近似最优解。否则,继续执行步骤4。根据作者的实验,本研究的最大迭代次数设置为100 000次。
计算访问概率:如果未达到最大迭代次数,则根据等式(8)计算i城市中的蚂蚁k移动到j城市的概率。重复步骤1-3。
停止准则2:如果每只蚂蚁都完成了从巢穴到食物源经过所有城市的路径结构列表,那么最短路径就是一个近似最优解。否则,进行如式(10)和式(11)所示的信息素更新过程,更新信息素的增强。然后,回到步骤4。
请注意,在任何迭代中,当获得较短的路径时,都会确定适当的解决方案,然后对这三个参数重新离散新的搜索空间。
3 仿真实验
3.2 SVRCACO交通预测模型
对SVRCACO模型进行滚动预测,采用1 h超前预测策略。然后,考虑几种类型的数据滚动来预测未来一小时的交通流量。本研究使用CACO算法来确定SVR模型中这三个参数的适当组合。选取测试NRMSE值最小的SVRCACO模型参数作为最适合本研究的模型,如表1所示。
当分别使用15和35个输入数据进行早晚交通流量预测时,SVRACO模型的性能最好。如表2所示。
比较了SARIMA和SVRCACO模型在NRMSE方面的预测精度。表2中“031106”表示2019年3月11日6点,依此类推。结果表明,SVRCACO模型比SARIMA模型具有更好的预测效果。
4 总结
准确的交通预测对于城市交通控制系统至关重要,特别是在高峰期避免拥堵和提高有限交通资源的效率。武汉市的历史交通数据表明,在许多城市高架交通系统中出现了季节性波动趋势。因此,交通流量的过度预测或预测不足会影响城市交通系统的运输能力。本文介绍了结合SVR和CACO的算法模型在城市间高速公路交通流量预测中的应用。实验结果表明,所提出的预测模型比常见的基于时间序列的预测模型具有更好的预测性能。
参考文献
[1] 邓烜堃,万良,丁红卫,等.基于深度学习的交通流量预测研究[J].计算机工程与应用,2019,55(2):228-235.
[2] 马全党,江福才,范庆波,等.PSO-无偏灰色马尔科夫模型在船舶交通流量预测中的应用[J].中国航海,2019,42(1):97-103.
[3] 李建森,沈齐,范馨月.城市道路短时交通流量预测[J].数学的实践与认识,2019,49(5):192-197.
[3] 范腾腾.城市道路交通流量短时预测研究[D].北京:北京交通大学,2012.
[4] 钱伟,车凯,李冰锋.基于组合模型的短时交通流量预测[J].控制工程,2019,26(1):125-130.
[5] 农昭光,李祖文,何增镇,等.基于自匹配数据融合模型的城市交通路况诱导系统[J].信息技术,2018(11):148-152.
[6] 李会超,李鸿,张博.基于遗传算法优化小波神经网络的短时交通流量预测[J].计算机应用与软件,2018,35(7):148-152.
[7] 范庆波,江福才,马全党,等.基于PSO的BP神经网络-Markov船舶交通流量预测模型[J].上海海事大学学报,2018,39(2):22-27.
[8] 邓烜堃,万良,丁红卫,等.基于深度学习的交通流量预测研究[J].计算机工程与应用,2019,55(2):228-235.
[9] 王秋莉,李军.基于核学习方法的短时交通流量预测[J].计算机应用研究,2019,36(3):696-700.
[10] 左霞,趙坚.耦合AF-SVR的短时交通流量预测模型[J].数学的实践与认识,2017,47(20):129-133.
[11] 罗文慧,董宝田,王泽胜.基于CNN-SVR混合深度学习模型的短时交通流预测[J].交通运输系统工程与信息,2017,17(5):68-74.
[12] 李丹,郭芝韵,朱延涛.基于ACO-SVR的混凝土坝变形监控模型[J].中国农村水利水电,2017(5):37-41.
[13] 曹成涛,林晓辉,许伦辉.联合FCM与群集蜘蛛优化SVR的短时交通流量预测[J].中国电子科学研究院学报,2017,12(1):52-59.
[14] 韩志聪,樊彦国,吴会胜,等.基于GA-SVR模型的短期交通流量预测方法研究[J].公路交通科技,2017,34(1):130-136.
[15] 姚卫红,方仁孝,张旭东.基于混合人工鱼群优化SVR的交通流量预测[J].大连理工大学学报,2015,55(6):632-637.
(收稿日期: 2019.07.17)

