“V排=S容·Δh”的理解及应用

张 玲

(湖北省武汉外国语学校 430056)

一、一道例题引发的疑惑：

例题为了测出玻璃的密度，小明同学利用一个玻璃制成的小瓶、一个大量筒和水做了如图1所示的实验：先在量筒内盛入50cm3的水，然后让小瓶口朝上漂浮在量筒内水面上，这时水面与80cm3刻度线相平，再让小瓶口朝下沉没水中，这时水面与62cm3刻度线相平.请你根据以上数据计算出这只玻璃小瓶的密度(g取10N/kg).

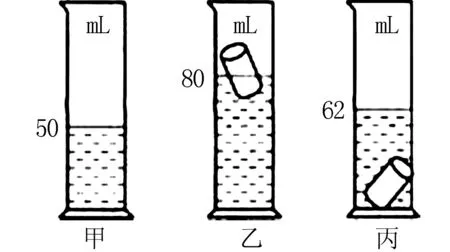
图1

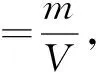
乙图：玻璃瓶漂浮，则玻璃瓶重G=F浮，

对比甲和乙图，V排=80cm3-50cm3=30cm3=30×10-6m3，F浮=G排=ρ水gV排=1×103kg/m3×10N/kg×30×10-6m3=0.3N；G=F浮=0.3N，

玻璃瓶的质量：m=0.03kg=30g；

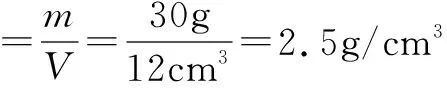
学生的疑惑对比甲和乙图，为什么V排=30cm3, 排开液体的体积应该小于30cm3呀！还有，物体浸入液体中会导致液面升高，那么V排和液面的升高量Δh之间有什么关系呢？

学情分析学生的前一个问题是个个性化的问题，很容易引导学生想明白：甲图中，V水=50cm3；乙图，V排+V水=80cm3，所以V排=80cm3-50cm3=30cm3. 学生的后一个问题对于很多同学来讲可能都存有疑惑，有的学生认为V排=S容·Δh，有的学生认为由容器的形状决定；有的学生认为V排=(S容-S物)·Δh……

看来，对于V排和容器底面积S容以及液面升高量Δh之间的关系，同学们并没有真正建立起科学的理解，大多是凭感觉作出猜测.如果缺乏对V排=S容·Δh正确的理解，那么在应用阿基米德原理解决浮力等一系列问题时一定会思维受阻，从而影响学习能力的提升.

奥苏伯尔说：“如果我必须将教育心理学的全部原理归结为一句话，那么我将会说，影响学生最重要的一个因素乃是学生已经知道的东西，肯定这一点并据此教学.” 教师的“教”是为学生的“学”服务的，“站在学生立场”即从学生的需求出发并据此进行教学.下面，笔者将从学生的疑惑点出发，帮助学生拨开迷雾见到月明.

二、展示推理过程，提高思维能力

1.“V排=S容·Δh”适用于什么样的容器？

由于V=Sh，这是柱体的体积计算公式，因此，“V排=S容·Δh”适用于柱形容器，如长方体、正方体、圆柱体等柱形容器，如图2.

图2

2.当物体在柱形容器的液体中沉底、悬浮、漂浮时，“V排=S容·Δh”都成立吗？

(1)物体沉底.柱形容器的底面积为S容，里面装有少量水，水深为h1, 将底面积为S物的长方体物块放入水中后，物块沉底，此时水深为h2，如图3和图4.

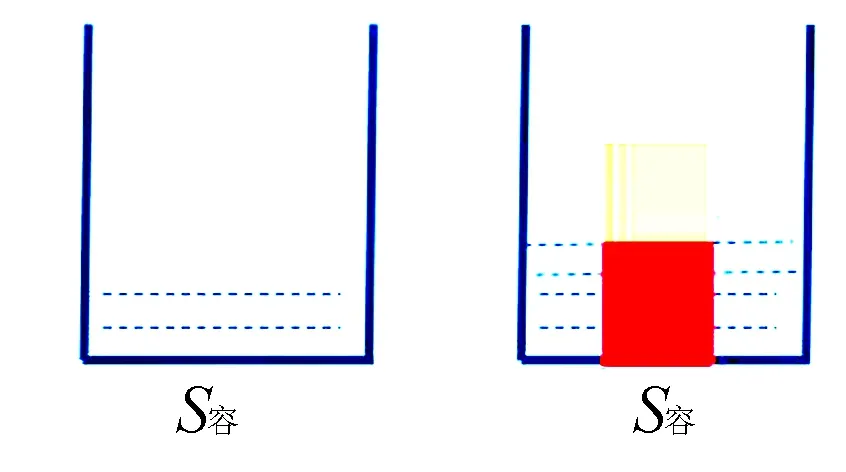
图3 图4

因为容器中水的体积V水不变，S容h1=(S容-S物)h2，将式子移项，S物h2=S容(h2-h1)，S物h2是物体浸在水中的体积，也就是物体的排水体积V排，h2-h1是液面的升高量Δh，即：V排=S容·Δh.因此，当物体在柱形容器的液体中沉底时，V排=S容·Δh成立.

(2)物体悬浮.柱形容器的底面积为S容，里面装有适量水，水深为h1, 将体积为V物的物块放入水中后，物块悬浮，此时水深为h2，如图5和图6.

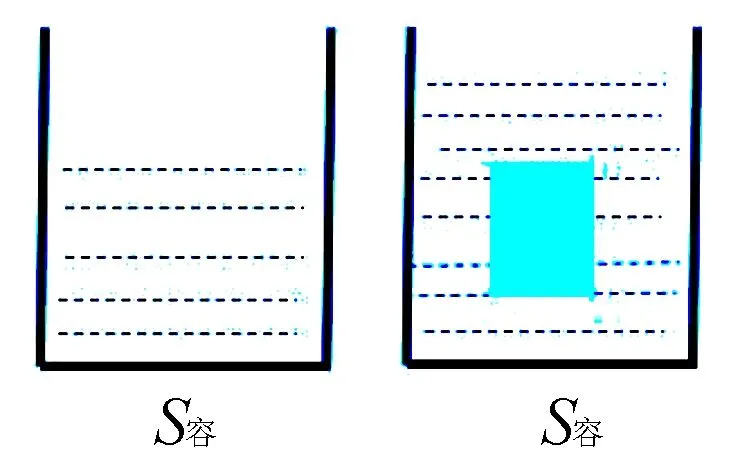
图5 图6

从图5和图6可知，S容h2=S容h1+V物，将式子移项，可得：V物=S容(h2-h1).由于物体浸没，V排=V物，液面的升高量Δh=h2-h1，所以，V排=S容·Δh

因此，当物体在柱形容器的液体中浸没时，V排=S容·Δh也成立.

(3)物体漂浮.柱形容器的底面积为S容，里面装有适量水，水深为h1, 将体积为V物的物块放入水中后，物块漂浮，此时水深为h2，如图7和图8.由图7和图8可知，

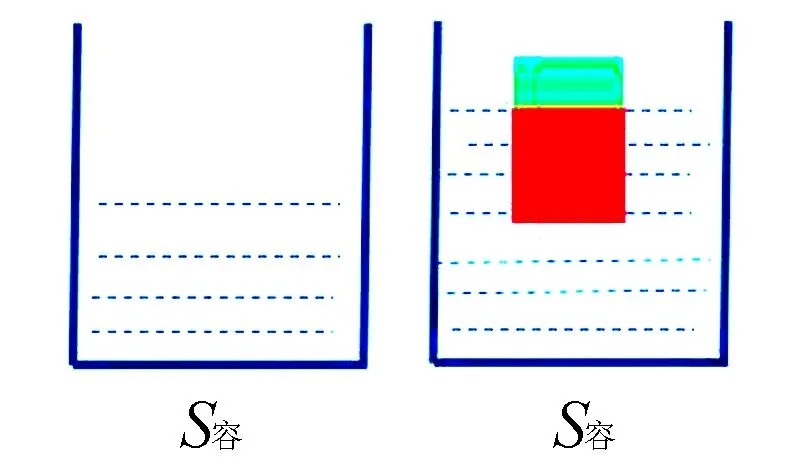
图7 图8

S容h2=S容h1+V排，将式子移项，可得：V排=S容(h2-h1)=S容·Δh.因此，当物体在柱形容器的液体中漂浮时，V排=S容·Δh仍然成立.

综上所述，当物体在柱形容器的液体中沉底、悬浮、漂浮时，“V排=S容·Δh”都成立.

三、应用“V排=S容·Δh”解决问题

1. 求浮力

例题在一底面积为8dm2装水的立方体容器中，投入一个含有3cm3砂子的冰块，水面上升了2cm,求冰和砂子受到的浮力.(g=10N/kg)

解题过程含有砂子的冰块在水中处于什么状态呢？是沉底？悬浮？还是漂浮呢？其实，我们根本不用考虑它在水中所处的状态，根据阿基米德原理和V排=S容·Δh，可以很容易求出它受到的浮力：

F浮=ρ液gV排=ρ液g·S容Δh

=1000kg/m3×10 N/kg×0.08m2×0.02m=16N

2.求压强

解题过程：

例题一个质量为0.6kg，边长为10cm的正方体物块，放置在水平桌面上，如图9所示，g取10N/kg．

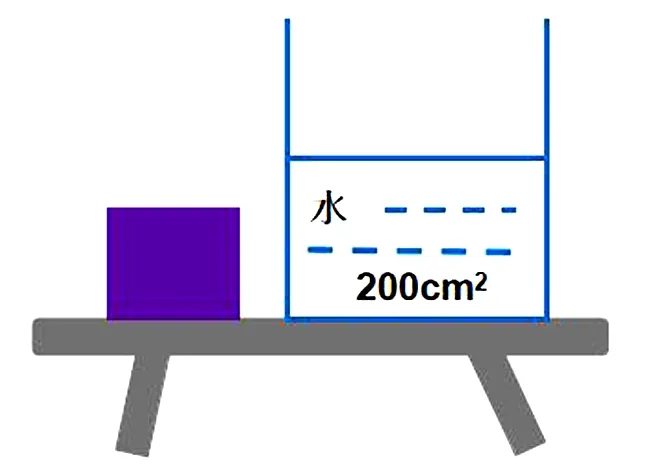
图9

(1)若将物块投入底面积为200cm2的圆柱形容器的水中(水未溢出)，求物块静止时受到的浮力．

(2)物块投入前后，水对容器底的压强变化了多少？

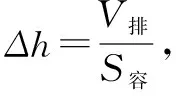
ρ物<ρ水， 物块静止时漂浮在水面上，则F浮=G=mg=0.6kg×10N/kg=6N.

投入物体后，水面升高量

压强增大了ΔP=ρ水gΔh=1.0×103kg/m3×10N/kg×3×10-2m=300Pa.

3.求密度

例题一块冰内含有一小石块，放入盛有水的量筒内，正好悬浮于水中，此时量筒内的水面升高了4.6cm．当冰熔化后，水面又下降了0.44cm．设量筒内横截面积为50cm2，则石块的密度为____(ρ冰=0.9×103kg/m3)

解题过程当物体悬浮在水中时，水面上升，可以利用V排=S容·Δh求出冰和石块的总体积；当冰熔化之后，水面下降，可以利用V排=S容·Δh计算出冰化成水之后减小的体积，从而再求出冰的体积.

悬浮时，V冰+V石=SΔh1=50cm2×4.6cm=230cm3

冰熔化后，水面下降Δh2，

V′=SΔh2=50cm2×0.44cm=22cm3

由于m冰=m水，可得：ρ冰V冰=ρ水V水

因此，V冰=220cm3,那么V石=230cm3-220cm3=10cm3

冰和石块悬浮于水中：F浮=G冰+G石

ρ水g(V冰+V石)=ρ冰gV冰+ρ石gV石；

在教学过程中，教师要时刻关注学生的疑惑点，在学生最需要帮助的地方抓住教育的契机，通过适当的引导、精确的实验、缜密的分析、科学的推理帮助学生建立正确的物理观念、提高思维品质、发展综合能力.正如2020年春季这场突如其来的疫情一样，虽然困难巨大，但它早已被全国人民众志成城团结一心的行动战胜而逐渐成为一段刻骨铭心的记忆！同样，只要我们在教学中一以贯之的“关注学生的疑惑点”并为其助力，当学生在学习困难之处生长出崭新的理解，那么教育一定会在学生的成长过程中留下一点点温馨难忘的印记.