昌九工业走廊工业化指数空间分布研究
叶俊锋, 周为吉, 温汉锋, 程小曼
(广东工业大学 管理学院, 广州 510520)
以昌九工业走廊12区11县3市为研究对象,利用主成分分析法计算出衡量工业化发展程度的工业化指数。从空间统计分析的角度入手,基于Arcgis和Geoda软件,利用莫兰指数对其工业化指数进行自相关分析,分析昌九工业走廊2016年各县、市、区工业化指数的空间分布状况。这种分析目的在于更加直观地展示昌九工业走廊各区域的工业化水平,分析工业走廊面临的发展机遇与阻碍因素,为该地区的工业发展提出合理的建议[1]。
1 文献综述
工业化指数的计算涉及多种数据多项指标,但指标之间存在数据的重叠。而主成分分析是指通过降维的方法,将多个存在相关关系并存在重叠信息的指标重新排列组合,此方法将原指标重新组合成一系列数量较少,独立性强且能尽可能保留原数据信息的综合指标,以达到提高分析结果的精确性和可靠性目的。其基本步骤可归纳为以下几步:A 将原始数据进行标准化处理;B 计算标准化数据的相关矩阵;C基于特征值确定主成分;D根据特征向量、特征值和累计贡献率通过主成分计算综合指数;E把综合指数规格化处理,将指数进行排序评价[2]。
空间统计分析指的是把传统统计分析的维度拓展到空间领域,把空间信息嵌入传统的统计方法中,用以探索研究对象属性的空间特征与空间结构。20世纪70年代,Tobler曾提出一个重要的地学观点,即事物的相关性随距离缩减而增强,随距离增加而削弱[3]。国外学者将空间统计分析理念拓展到多学科并对原学科的研究方法进行改进,包括生物学和传统地学等学科,其中空间计量经济学获得极大的发展。
国内学者对于空间统计学研究领域比较狭窄,目前多着眼于空间统计模型的应用,包括犯罪分布特征分析,流行病追踪和经济地域分异分析等方面。其中,席路瑶利用贵州省人均工业产值作为观测属性,探索省内各区域工业发展水平的空间分布特征并提出产业布局调整建议[4];王俊松利用面板数据和空间趋势分析探讨了中国城市技术创新能力的空间分布[5];袁媛基于空间统计方法对南昌市景观生态安全水平构建了评价体系[6];颜仕鹏利用克里金插值分析、空间聚类分析和全局趋势分析建立模型,探索了湖南省恶性肿瘤的发病和死亡分布的空间特征[7]。
2 研究方法与数据来源
2.1 研究思路与方法
本文研究思路如下,首先要计算工业走廊各县域工业化指数,利用多项指标,通过主成分分析得到工业化指数,并作为空间自分析的重要指标,通过Arcgis和Geoda软件进而分析昌九工业走廊2016年各县、市、区工业化指数的空间分布状况,通过量化分析和可视化的方式探索与展示各区域工业水平之间的空间关系。
2.1.1 主成分分析
基于因子降维的思路,通过主成分分析把各项衡量工业化程度的原始指标进行降维,压缩成能够保留原始信息且具有独立性的少数新指标。
1)制作原始指标矩阵,每个观测值有j个评价指标,i个主体,构成i×j阶矩阵X:
2)原始变量Xij减平均值再除标准差,实现原始变量的标准化,得到标准化数据Zij:
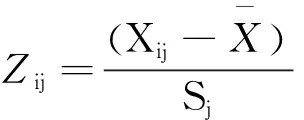
(1)
3)以矩阵Z=(Zij)为基础,计算相关系数矩阵R=(rjk),其中:
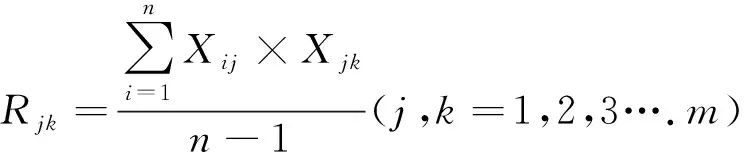
(2)
4)求矩阵R的特征值λ1>λ2>… >λp及单位特征向量ej(e1j,e2 j,…,epj) ,特征值大小决定主成分是否具有统计意义,而方差的贡献率说明主成分对信息的保留程度。
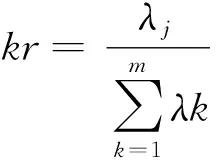
6)基于主成分,特征值与特征向量,获得主成分得分Yj,对Yj利用贡献率进行加权求和运算,获得综合评价指数。
2.1.2 空间自相关分析
通过Geoda的空间全局自相关分析和空间局部自相关分析,可以度量观测值在空间上的整体分布特征与相互依赖性,以及其在局部空间的集聚程度[8]。先要构筑空间权重矩阵,才能进行空间自相关分析[9]。
1)构建空间权重矩阵。空间实体i对实体j会随空间关系的差异而产生的不同程度的影响,其中包括邻接、连通等空间关系,而i对j的影响在二维平面上显示为带有权重的矩阵W。其形式如下[10]:
空间实体落在n个空间单元中,实体i对j的影响用wij表示,一般而言,将矩阵中的邻接(拥有公共边界)的空间实体关系赋值为1,其他非邻接关系赋值为0,形式如下:
2)求全局空间自相关指标。莫兰指数是属于空间自相关系数的一种,用以衡量具有空间邻接或连通关系的空间实体某属性观测值之间的相关程度[11],通过以下公式可以计算26各县域整体工业化指数的莫兰指数并反映其空间分布特征, 公式如下:

(3)
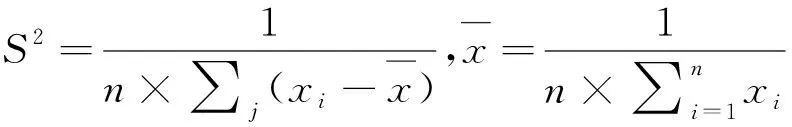
式中:I为莫兰指数;xi为区域i的观测值;wij为空间权重矩阵元素。
3)求局域空间自相关指标。莫兰指数是从全局宏观角度研究26个县域整体的工业化指数的空间分布特征,如果要从局部的角度分析各县域具体的相关性,需要利用“空间关联局域指标”(LISA),公式如下:

(4)
2.2 数据来源
本文采取的数据为昌九工业走廊地理空间分布 Shapefile 格式数据, 数据主要包括2016年昌九工业走廊12区11县3市经济数据和行政信息(图1)。数据来源于国家统计局以及江西省各市统计年鉴。

图1 昌九工业走廊行政区划图
3 实证研究
3.1 研究区概况
昌九工业走廊是江西省政府于九十年代计划在南昌和九江这两座城市之间建立起可带动省经济发展的工业经济带。但由于各种原因停滞不前,直到21世纪初国家开始推动中部地区经济崛起,江西省重启昌九工业走廊计划,目的在于将工业走廊塑造成江西省新的经济增长引擎,在拉动经济发展和促进产业转型升级的同时,建设成华东地区先进的工业研发与生产基地。
昌九工业走廊地理范围覆盖南昌、九江两个地级市,范围囊括12区11县3市。作为拉动江西其他城市及周边较落后地区经济增长的“马车”,形成扩散效应,它的成绩与优势能够吸引活性资本的投资与人才的落户,更能得到国家的青睐和支持,实现经济的跨越式发展。[12]。
3.2 工业化指数的确定
3.2.1 选取工业化指数评价指标
产业比重的变动,生产总值的跨越式增长以及居民收入的增加,是工业发展的表现。为了分析各县域的工业化程度,借鉴中国社科院关于中国工业化水平测算和评价体系构建的研究成果[13],本文选取了9个指标:X1代表人均生产总值,X2代表二三产业GDP占总GDP的比重,X3代表二三产业从业人员占总产业人员的比重,X4代表城镇化率,X5代表常住人口,X6代表初中毕业人数,X7代表工业总产值,X8代表工业增加值以及X9代表工业固定投资作为评价工业化指数的指标。
3.2.2 基于spss进行主成分分析
1)基于统计软件spss进行主成分分析。原始数据先进行标准化,再进行因子分析,根据Bartlett球型检验和KMO计算可知评价工业化指数的各项指标数据具有较强相关性,适合做主成分分析。
2)通过降维的主成分分析,得到总方差解释表(表1)和成分矩阵(表2)。其中总方差解释表当中,9个指标经过降维旋转得到3个主成分因子,且特征值均大于1,累计贡献率也达到了85.172%,因此该3个因子可以代表原指标。此外,从表3可知,工业总产值(X7)、工业增加值(X8)、工业固定投资(X9)在主成分因子F1上有较大的载荷值,因此F1可称为工业因子,同理,F2称为产业结构因子,F3称为人口因子。
3)下一步需要计算主成分载荷矩阵U。载荷矩阵元素Ui是由成分矩阵A除以特征值λ的开方所得的商值,Ui的计算公式如下:

(5)
因此,已知成分矩阵A和特征值λ,可求U。
4)利用spss 23软件,通过公式5,得到特征向量U1和U2和U3,两者合起来就是主成分载荷矩阵。由此可以得到主成分计算公式:
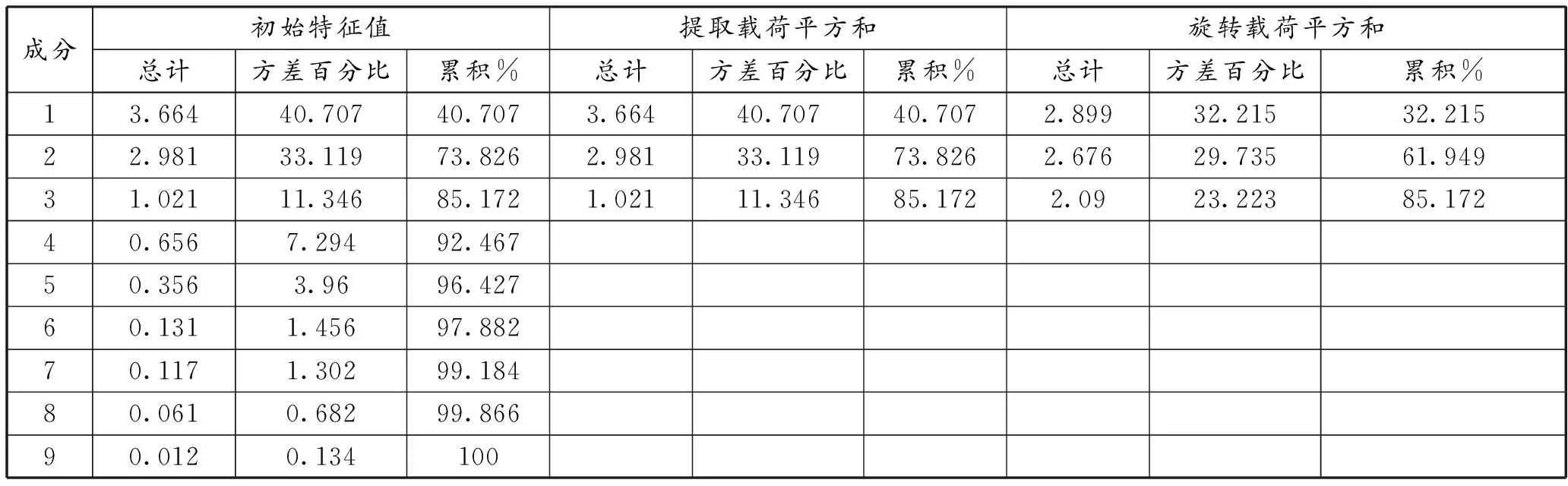
表1 总方差解释

表2 旋转后的成分矩阵表
Y1=0.36766X1+0.14566X2-0.04816X3+0.00117X4+0.02937X5+0.07929X6+0.56324X7+0.57734X8+0.42816X9
Y2=0.36984X1+0.50860X2+0.50371X3+0.47315X4-0.08130X5-0.31115X6-0.04157X7+0.01345X8+0.14732X9
Y3=-0.25663X1-0.17985X2-0.27115X3+0.04012X4+0.65298X5+0.53954X6+0.03735X7+0.02006X8+0.32787X9
5)依据主成分计算公式,得到Y1,Y2,Y3并通过Y=(Y1*贡献率1+Y2*贡献率2+Y3*贡献率3)/总贡献率,得到工业化评价指数Y并规格化处理。其中贡献率1为32.215%,贡献率2为29.735%,贡献率3为23.223%,总贡献率为85.172%[14]。
基于2016年12月底昌九工业走廊行政规划图,利用Arcgis软件将工业化指数进行可视化(如图2),方便进行进一步分析。
从上述工业化指数表可知,南昌高新开发区、南昌县、南昌经济开发区、青山湖区、九江开发区是综合得分排名前五的地区,这五个地区的工业化指数排名与GDP排名一致。五个地区中,其中三个被冠以“开发区”的名义,注重发展新型工业,南昌高新开发区是国家级高新区,拥有千亿级别的产业园区,因此产业结构比重以及产值比重中工业都占优势,而南昌经济开发区是江西第一个国家级经济技术开发区,以吸引外资办厂为主要发展方向,拥有深厚的工业发展基础与规模,九江开发区情况与前两个地区类似。而南昌县和西湖区则属于老牌的工业区域。
彭泽县、都昌县、安义县、武宁县、湾里区则是综合得分排名中的倒数前五名,工业化指数排名与GDP排名一致。这五个地区工业总产值较低,工业固定投资不高,缺乏强势的产业园和可带动当地经济发展的规模工业,因此工业化程度不高。
3.3 空间自相关分析
3.3.1 全局空间自相关分析
1)构建空间权重矩阵。通过Arcgis将昌九工业走廊的行政图矢量化并赋予各县域工业化指数的属性值,再将矢量图形输入Geoda中,利用Geoda软件针对工业化指数这一个属性值构建空间权重矩阵。
2)空间关联性分析。基于空间权重矩阵可以绘制Moran(莫兰)散点图。莫兰散点图以坐标轴和点的形式来表现被观测的属性值在空间上的分布特征与相关程度。散点图共有四个象限,按其性质分为高高(第一象限)、 低高(第二象限)、 低低(第三象限)、高低(第四象限)。
落入“高高”象限和“低低”象限的空间单元都有较强的空间正相关性质。其中“高高”象限表示某一单元和周围单元的属性值都较高,而两者组成的区域被称为热点区;“低低”象限表示某一单元和周围单元属性值都较低,会产生冷点区。“高低”表示该空间单元属性值较高,而周围单元较低,“低高”则刚好与此相反,落入这两个象限的空间单元存在较强的空间负相关性质。

表3 各地区工业化的主成分得分和综合得分
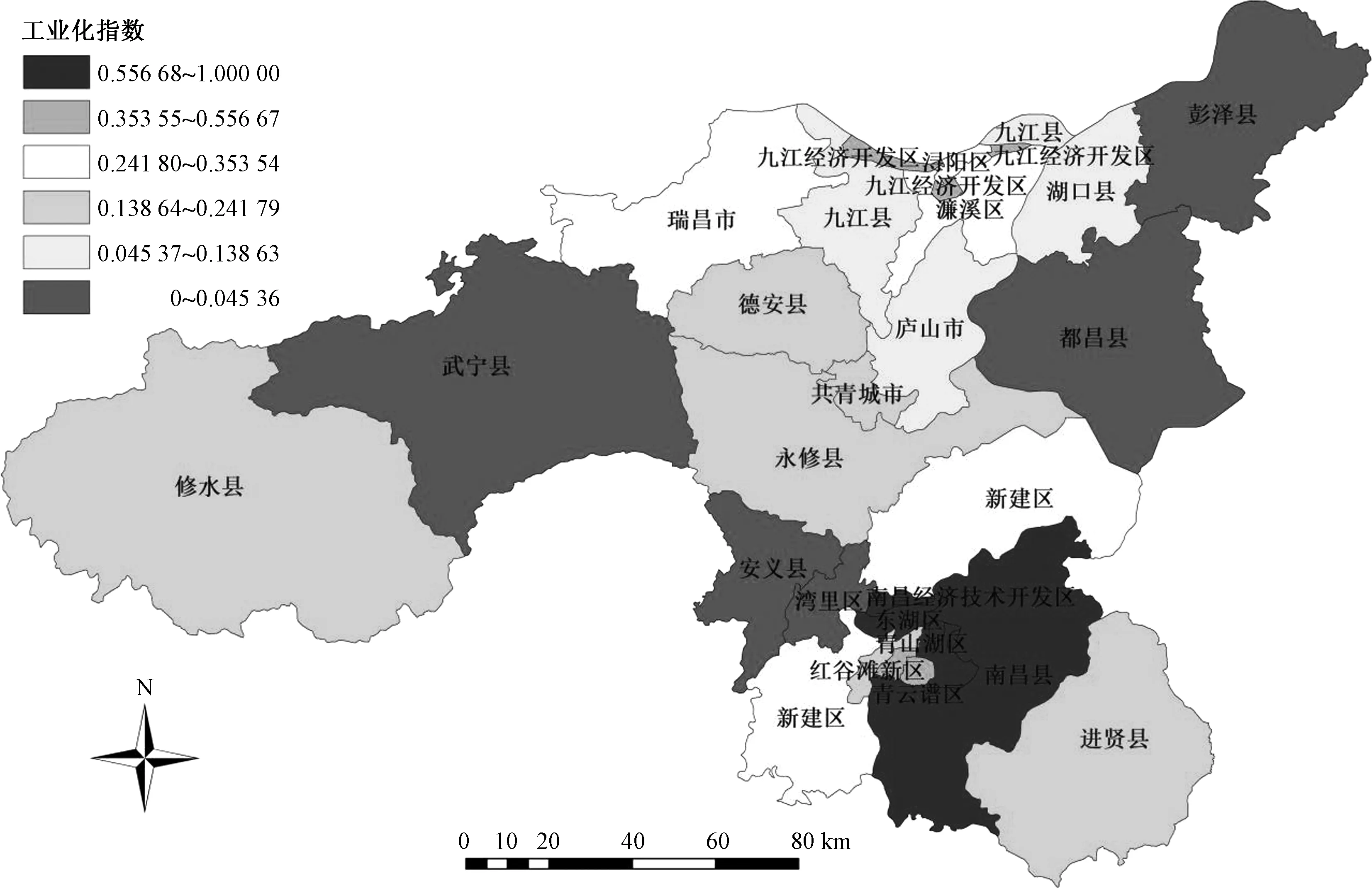
图2 昌九工业走廊工业化指数分布图
3)昌九工业走廊各县域工业化指数全局空间自相关分析。空间自相关指数是对物体空间关系的数据化表征。通过Geoda1.12软件,构建空间权重矩阵,并对昌九工业走廊26个县域的工业化指数进行全局自相关分析,得到全局莫兰指数,Moran’s I=0.458477,莫兰指数大于0,可知26个县域工业化指数都具有较大的空间正相关关系,即昌九工业走廊各县域的工业化指数表现出空间聚集的形态。由Geoda1.12软件生成的莫兰散点图(图3)可知,26个工业化指数点多分布在第一和第三象限,其表现出一定的空间关联特征:工业化指数较高的县域倾向和工业化指数较高的县相邻,形成热点区域,属于“高高”集聚;工业化指数较低的县域倾向和工业化指数较低的相邻,形成零点区域,属于“低低”集聚。在第一象限和第三象限的地理单元都存在较强的空间正相关关系。
此外,通过蒙特卡罗检验(图4)全局莫兰指数的显著性,得到显著性水平指数P=0.001000,符合(-∞,0.01)的范围,临界值Z=4.1354,符合(-∞,-2.58)或(2.58,+∞)的范围,也就是表明全局莫兰指数在 99.9% 置信度下的空间自相关是显著的。

图3 莫兰散点图
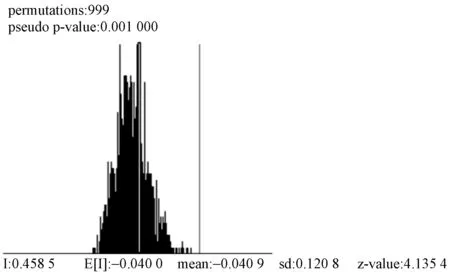
图4 蒙特卡罗模拟图
3.3.2 局部空间自相关分析
莫兰指数是度量全局空间自相关关系的指标,用以确认空间实体被观测的属性值是否具有宏观意义的相关性和相关性大小。而局部空间自相关分析是利用LISA聚类图,从微观角度展示一片区域中每个观测实体的属性值和相邻实体属性值的具体相关程度[15]。
基于Geoda1.12软件,通过空间统计工具中的“异类和异常值分析”功能,对26个县域的工业化指数进行空间局部自相关分析,得到一系列LISA值。在Arcgis通过空间可视化的方式,将局部自相关的聚集情况用图表现出来(图5)。其中红色代表高高聚集, 表明南昌县、青云谱区、青山湖区、南昌高新开发区、西湖区的工业化指数和其周边县域的指数都较高; 蓝色代表低低聚集,表明永修县、德安县、湖口县工业化指数和其周边县域的工业化指数都较低;紫色代表低高聚集,表明该县域的工业化指数远低于其周边县域工业化指数,如红谷滩新区和进贤县;粉色代表高低聚集,表明该县域的工业化指数远高于其周边县域的指数,而灰色则为不显著。
造成这种分布的原因主要是昌九工业走廊区域内经济发展层次不一,九江市第一产业所占比重仍然较多,比如以酿酒闻名的九江县以及都昌县,工业化水平不高,产品附加值较低,使当地居民生活品质和经济发展水平都落后于其他地区。而南昌县、青云谱区、青山湖区、西湖区,第二第三产业发达,因此工业化指数较高。
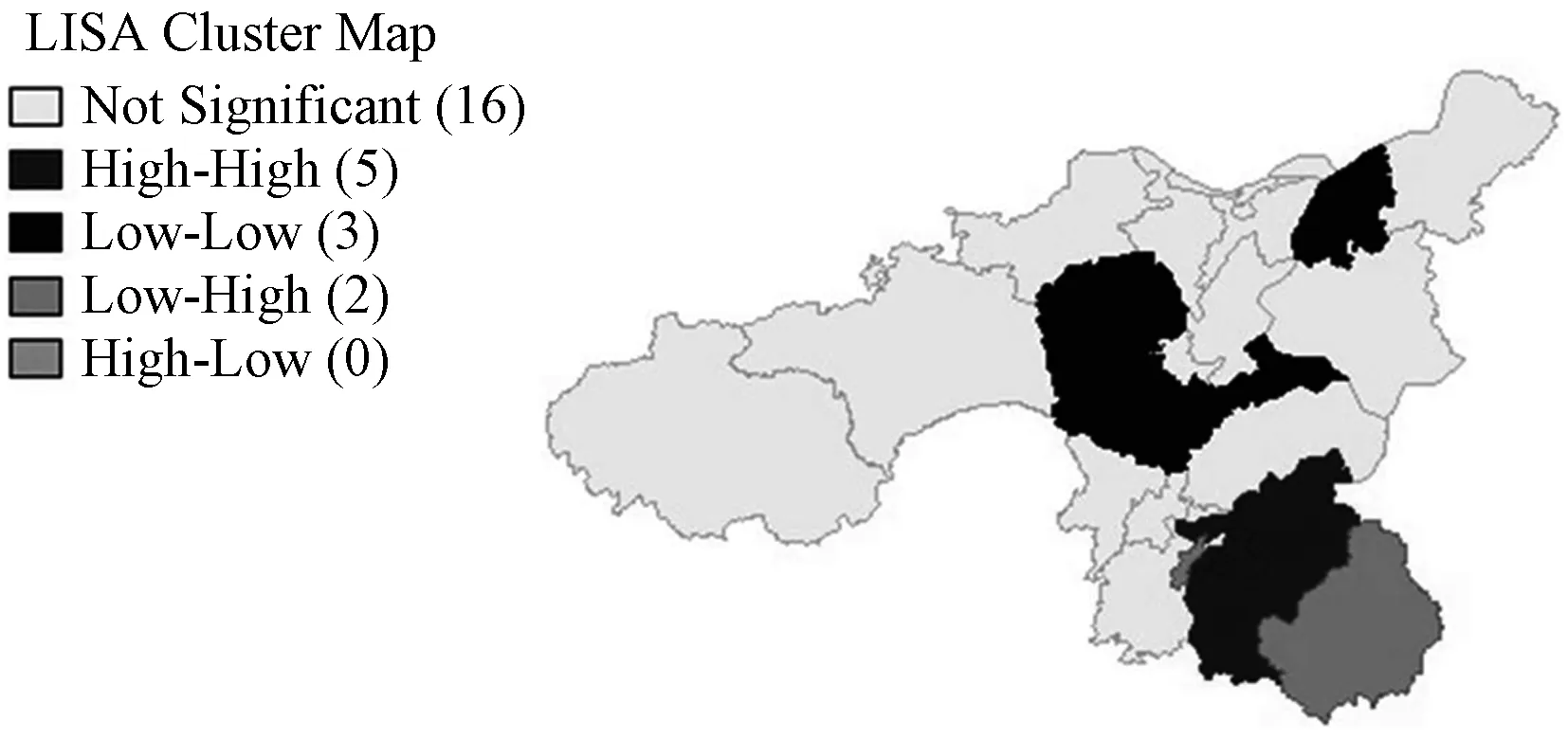
图5 LISA聚类图
4 结论
本文以2016年昌九工业走廊各县域的九个指标进行主成分分析,计算得出代表地区工业化水平的工业化指数作为衡量指标。
以工业化指数数据为支撑, 对各个县域进行了空间自相关分析。首先是全局空间自相关分析,得出该时期内昌九工业走廊各县域的工业化指数在空间关联性上成正相关,工业化指数展现出了高度的空间聚集。其次是局部空间自相关分析,得到26个县域具体的集聚情况以及集聚显著度。
从空间分析结果可以得知各地工业化程度的差异。昌九工业走廊中,九江市行政区划内的各地区普遍工业化指数较低,这是由于九江市较高的第一产业比重较高,且工业产值不足,缺乏可带动经济增长的规模工业,相比之下南昌市行政区划内的地区工业化水平都比较高。昌九工业走廊要因地制宜地制定发展规划。对于九江市、都昌县这种以特色型第一产业占主导地位的地区,不要盲目发展大规模工业,应适当地发展特色加工工业和特色旅游业等第三产业;对于工业化程度较高的南昌高新技术开发区、南昌县等地区,应该适时进行工业升级,响应国家政策,开展低能耗少污染高附加值的新型产业建设。
基于Arcgis和Geoda软件对昌九工业走廊的工业化指数进行空间相关分析,通过数据以及可视图的形式直观地展现分析结果,具有一定的优势。当然还存在很多不足, 由于研究对象太过详细,九江与南昌统计年鉴中提供的各县域数据比较笼统,因此在计算工业化指数时选取的指标有限。在今后的研究中也可以尝试进行空间回归模型的分析。此外, 区域工业化的发展还受到生态环境治理以及消费水平等多种因素影响,这些因素对工业化水平发展产生的影响还有待探讨。

