无网格法在土质边坡稳定工程中的应用

臧 贻 甜

(山东省潍坊基础工程公司，山东 潍坊 261061)

1 概述

滑坡是一种常见的地质灾害，给工程建设带来巨大损失。目前，再现岩土工程力学行为的手段有两种，即实验研究和数值模拟。针对土质边坡稳定的平面应变问题，常利用数值模拟法，即假设工程土性质符合Drucker-Prager本构关系，基于相关流动法则，采用强度折减系数法得到土质边坡在自重作用下的安全系数。文章基于无网格法编制了计算程序，结合工程实际并与有限元法计算结果进行对比，结果表明采用无网格法能克服数值计算中网格畸变问题，适于解决土质边坡稳定问题。

2 无网格法简介

无网格法的近似函数不依赖于网格，而是采用基于点的近似函数。所以在解决边坡稳定等可能引起网格拓扑关系的问题上比有限元法方便实用。无网格法的这种性质使得为了得到离散的代数方程组仅需要对节点和边界条件进行描述即可，从而避免了大量的单元网格划分工作，并且克服了有限元法中由于场函数的局部化近似所引起的误差。文章研究了利用伽辽金无网格法计算土质边坡稳定问题，其基本函数如下。

移动最小二乘法是用加权最小二乘法来近似场函数的一种方法。从数学理论上讲，最小二乘法描述的是函数逼近问题，即最小二乘逼近。

设函数u(x)在域Ω中的N个节点xI(I=1,2,…,N)处的值uI=u(xI)是已知的，u(x)的全局近似函数为uh(x)，则u(x)在高斯点的邻域Ωx内可以局部近似为：

(1)

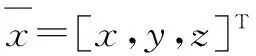
a(x)=[a1(x),a2(x),…,am(x)]T,ai(x)是待定系数。

3 无网格法的弹塑性理论

3.1 屈服准则

Drucker-Prager屈服条件的表达式为:

(2)

其中，α，k均为正常数。

平面应变问题:

(3)

其中，c为黏聚力;φ为内摩擦角。

3.2 加载和卸载准则

理想弹塑性材料[1]不发生强化，其屈服面的大小和形状不随内变量的发展而变化。其表达式为：

(4)

3.3 弹塑性本构矩阵的一般表达式

屈服条件用式(5)表示:

F(σij,K)=0

(5)

其中，σij为应力状态；K为硬化函数。

应用增量理论，弹性增量和塑性增量为：

d[ε]=d[ε]e+d[ε]p

(6)

其中，弹性应变部分与应力增量之间的关系服从胡克定律，即:

d[σ]=[D]d[ε]e

(7)

其中,[D]为弹性矩阵。

应用流动法得增量理论的弹塑性矩阵通式：

(8)

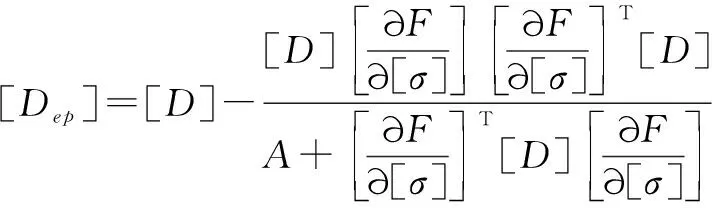
(9)

4 无网格法的程序实现

4.1 离散化方法

依据Belytschko等[3]的研究理论，把规则网格对域Ω的积分转化为对各规则格子(cell)的积分之和，然后再在每个规则格子中使用高斯积分，如图1所示。

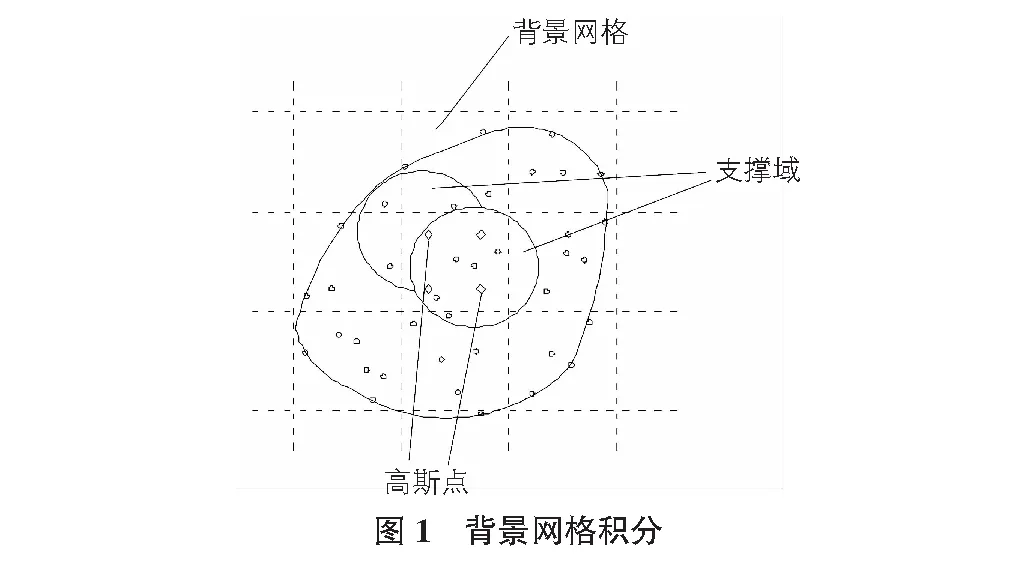
4.2 数值积分

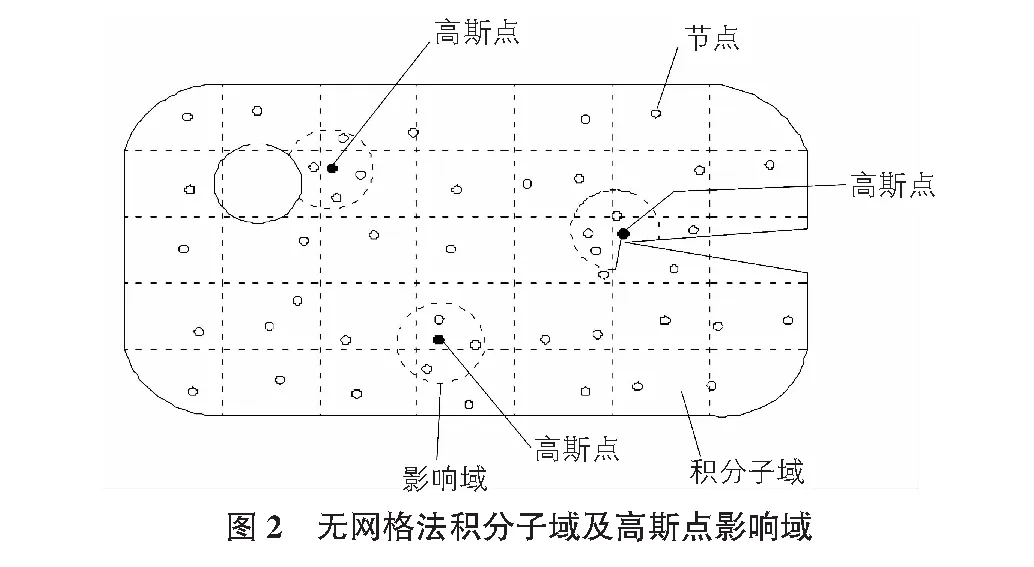
将计算区域划分为若干规则网格，在每一个子域上采用高斯积分。如图2所示，计算域Ω为图中实线所包围区域，图中各空心圆为节点，可采取规则布置或不规则布置。

5 土质边坡稳定计算

为验证无网格法解决土质边坡稳定问题的有效性，并与工程实践相结合，现以潍坊青州市民兵训练基地打靶场护坡工程为例进行验算，并与有限元法计算结果进行对比。该项目位于青州市弥河镇大马山东北，赤涧村正西，现场地形为坡度约1∶7的土质边坡，场地尺寸约为30 m×140 m，最大挖深约20 m，周围50 m范围内无建筑物和构筑物，拟采用1∶1放坡后喷锚支护方式，放坡后尺寸约80 m×160 m，不考虑地下水和地震对边坡稳定的影响。根据岩土工程勘察报告，其岩土基本参数为：土容重γ=19 kN/m3，粘聚力c=42 kPa，内摩擦角φ=17°。

如图3所示，根据平面应变建立计算模型(β=45°)，边界条件为左右两侧水平约束，下部固定，上部为自由边界，采用关联流动法则计算。

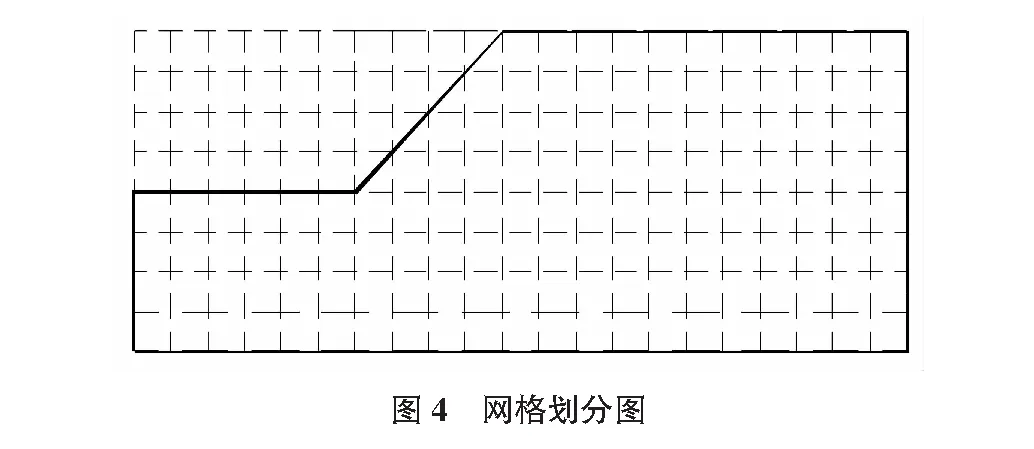
计算域内采用非均匀节点布置，在预期滑裂面周围适当增加节点的数量。采用21×8个积分背景网格，每个网格布置4个高斯积分点(2×2高斯积分)，其网格划分见图4。

为检验土体的变形模量和泊松比对土坡稳定安全系数影响，文章计算了有限元强度折减法与无网格法在不同土体变形模量和泊松比条件下的解。从表1，表2的计算结果可以看出土体的变形模量和泊松比对土坡安全系数的影响是非常小的，并且有限元解与无网格解是非常吻合的。

表3为有限元解和无网格法的计算结果，从表3中数值可以看到无网格法计算的结果是非常精确的。因此，利用无网格法求解土质边坡稳定问题是有效的。

表1 不同变形模量计算的最小安全系数

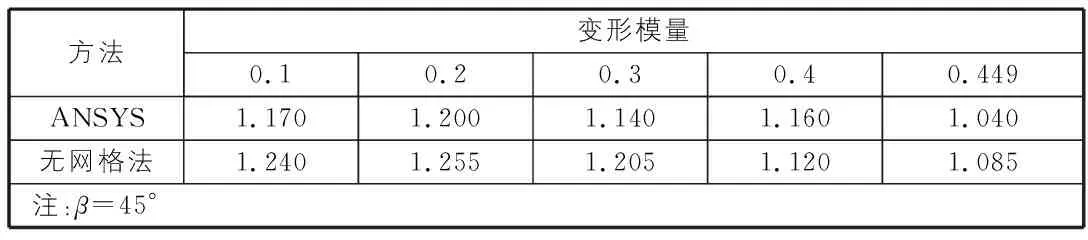
表2 不同泊松比计算的最小安全系数

表3 不同坡脚计算的最小安全系数

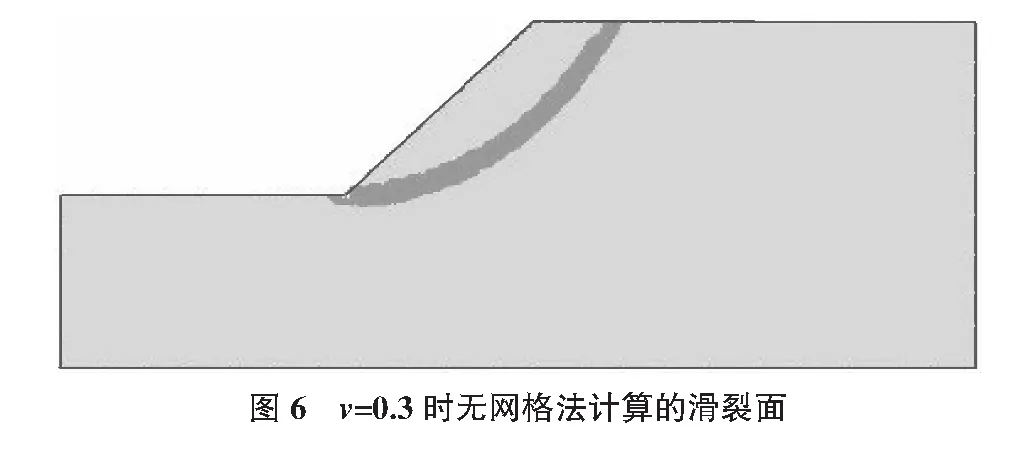
图5为该边坡有限元(ANSYS)计算收敛(泊松比v=0.3)时的塑性区分布，图6为无网格法计算的滑裂面形状，可以看出有限元法与无网格法所计算出的滑裂面的位置是非常接近的。

该工程通过利用无网格法确定了土质边坡破裂面的位置，为边坡支护设计提供了强有力的数据支撑。

6 结语

与有限元法相比，无网格法不需要划分单元，只需布置节点，特别适合于弹塑性等大变形问题的分析。文章计算了土质边坡稳定的安全系数，数值结果表明采用无网格法求解土质边坡稳定问题是有效的。