脑立体定向技术靶点误差影响因素分析

米 良，樊宇耕，张永兵，杨海贵，杜宏瑞

(延安市人民医院神经外科，陕西 延安 716000)

立体定向脑活检术(Stereotactic Brain Biopsy，SBB)以其安全、准确、微创等特点在颅内病变诊断中越来越受欢迎。作为一种以精确性见长的手术，必须充分认识误差的来源及大小，而这一误差产生体现在手术的全部过程中，如影像定位时产生的误差，计划系统产生的误差，手术操作时产生的误差等等，均有相关文献报道，但是对于靶点误差的范围，手术中靶点相关指标对靶点误差的影响报道寥寥无几。本研究利用颅骨模型，建立模拟靶点模拟立体定向手术过程，采用Leksell-G手术方法，测量靶点误差范围，分别对不同靶点位置的误差进行分析，探索靶点相关指标对立体定向活检术误差的影响因素，为临床工作中目标靶点的设置及穿刺路径的选择提供参考。

1 材料与方法

1.1 模拟靶点制作

选取成人颅骨标本沿冠状缝、双侧顶骨鳞缝、乙状缝去掉顶骨，完全暴露颅腔内部，其内设计模拟靶点，模拟靶点以特制钛合金电极片为材料，分别于前颅窝底两侧、中颅窝底两侧、后颅窝底两侧、垂体窝、颅底内面枕骨大孔处放置8个模拟靶点电极片,做为模拟靶点。

1.2 模拟立体定向手术

1.2.1 安装框架，完成影像扫描 将Leksell头架以四根螺钉固定于颅骨标本上，使其基环平面保持水平，用以模拟有框架活检手术影像定位和弧形弓架固定用。然后行颅脑CT定位扫描，层厚2.0 cm。进行伪影校正后，传输影像资料于Leksell-G型立体定向系统计算机计划软件中。

1.2.2 模拟立体定向手术，测量靶点误差 以每个模拟靶点中心点为计划靶点，设计穿刺路径模拟活检手术，记录每个靶点X、Y、Z、环角、弧角数值，按照设定数值依次于固定环对准Z值，安装固定环，于基环左右两侧对准Y值，安装弧形弓架对准X值，调整弧角、环角，由于颅骨阻挡等因素，根据实际情况适当更改弧角、环角数值，记录数据。于载物器固定导向夹，设定导向尺0点上0.5 mm，插入活检针，用电子数显游标卡尺测量活检针针头与模拟靶点中心点的距离，每个靶点均行三次测量取平均值。

1.3 统计学方法

数据以均数±标准差表示，应用SPASS 20.0软件进行统计学分析。单因素回归分析靶点相关因素与靶点误差的关系。不同靶点位置间的差异采用方差分析，P<0.05为差异有统计学意义。

2 结果

2.1 靶点误差

Leksell-G系统活检手术的平均靶点误差范围为(3.49±1.15)mm，其中前颅窝底靶点误差范围为(3.64±0.98)mm，中颅窝底靶点误差范围为(3.56±1.09)mm，后颅窝底靶点误差范围为(3.30±1.25)mm，垂体窝靶点误差范围为(3.44±1.43)mm，枕骨大孔靶点误差范围为(3.36±1.31)mm。

2.2 靶点位置对靶点误差的影响

对不同位置的靶点误差进行单因素方差分析，P值为0.910，无统计学意义(见图1)。把靶点位置划分为左侧大脑半球(左侧前、中、后颅窝底)、中线(垂体窝、枕骨大孔)、右侧大脑半球(右侧前、中、后颅窝底)三组，进行单因素方差分析，P值为0.870，同样无统计意义。

2.3 靶点坐标值对靶点的影响

对可能影响Leksell-G系统模拟手术靶点误差的X、Y、Z、环角、弧角数据进行单因素回归分析，结果显示：靶点位置的X、Y、Z坐标值对靶点误差无统计学意义(P值分别为0.908、0.813、0.836)。穿刺路径的环角和弧角对靶点误差的影响有统计学意义(P值分别为0.032、0.007)。环角、弧角度数越大，靶点误差影响越小，环角、弧角度数较小，靶点误差影响则较大(见表1)。

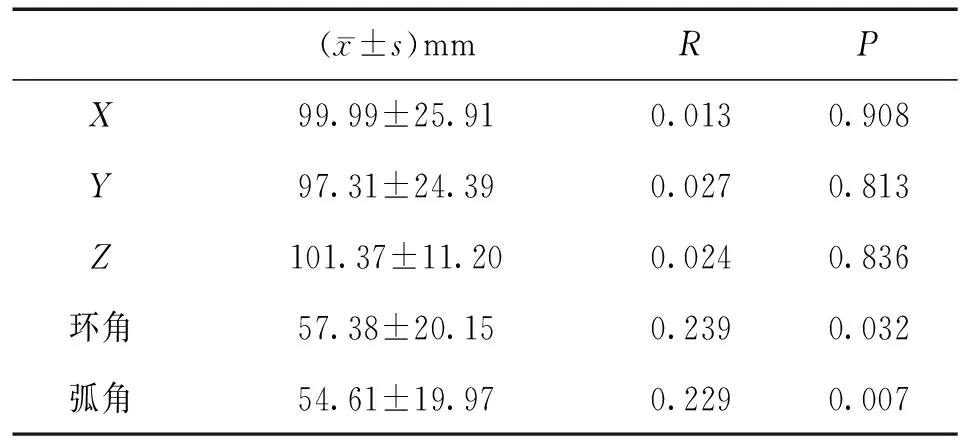
表1 Leksell-G系统影响因素的单因素回归分析

3 讨论

本研究通过颅骨标本设置模拟靶点模拟Leksell-G系统活检手术，直接测量活检针到达位置与实际靶点的距离，该距离即反映出靶点误差的范围。通过实验，Leksell-G系统活检手术的靶点误差范围(3.49±1.15)mm，宣武医院乔武，等[1]通过立体定向植入电极计算计划靶点与实际靶点之间的误差为1.4(0～4.6)mm，与实验结果基本吻合,且与其他相关文献报道误差值接近[2]。

立体定向手术系统由定位系统、导向系统、手术计划系统、脑内手术器械和辅助设备等多个部分组成，各系统协调精确地完成手术过程。然而所有设备在使用时均会产生一定的误差，如框架安装时产生的误差、影像定位时所产生的误差、立体定向仪器系统的误差等[3]。这些误差在一定的范围内相互影响，最终导致手术器械到达的位置与术前手术计划设定的靶点之间存在着一定的偏差。作为一种以准确性与微侵袭性见长的技术，靶点误差可能会影响到穿刺活检诊断样本的质量，从而影响到诊断的准确性及治疗的有效性。

有文献报道框架安装不正，左右倾斜和左右旋转可对靶点误差产生影响，螺钉用力不均匀、拧的过紧可能会导致框架的基环和固定杆发生变形，导致定位误差。Taub[4]报道框架绕Y轴每旋转3度可使靶点产生1 mm的移位。进行影像学定位时，CT可因噪声、层厚、回旋滤波、像素大小、图像处理、容积效应等因素对成像产生影响。Drzymala，等[5]报道CT扫描所得靶点坐标与Leksell定位系统的机械测量值相差为(0.78±0.33)mm。Yu，等[6]报道CT定位X、Y、Z轴的最大误差平均值分别为1.0(0.2～1.3)mm、0.4(0.1～0.8)mm、3.8(1.9～5.1)mm。而MRI可因主磁场的不均匀性、梯度磁场非线性、涡流效应、化学移位及磁敏感效应等因素可能导致影像的扭曲，且离影像中心越远，影像扭曲越严重，随着视野增大，影像周边的扭曲也越明显。Drzymala，等[5]报道MRI所得靶点坐标与Leksell定位系统的机械测量值相差(1.45±0.8)mm。Landi，等[7]报道MRI与模型的X、Y、Z几何测量值相差1 mm、2 mm、l mm。对于注册误差，数据采集方法可对靶点误差产生影响，通过采用二维数据重建三维图像与用三维数据直接成像的精确度进行对比证实，三维数据直接成像产生的靶点误差明显小于通过二维数据重建三维图像[8]。另外坐标转换方法也会对靶点误差产生影响。

本研究数据显示，Leksell-G系统中前颅窝底靶点误差范围为(3.64±0.98)mm，中颅窝底靶点误差范围为(3.56±1.09)mm，后颅窝底靶点误差范围为(3.30±1.25)mm，垂体窝靶点误差范围为(3.44±1.43)mm，枕骨大孔靶点误差范围为(3.36±1.31)mm。对各靶点位置进行方差分析，差异无统计学意义(P=0.910),说明靶点位置对靶点误差没有影响。把靶点位置划分为左侧大脑半球(左侧前、中、后颅窝底)、中线(垂体窝、枕骨大孔)、右侧大脑半球(右侧前、中、后颅窝底)三组，进行单因素方差分析，P值为0.87，各组间差异无统计学意义。

穿刺路径的环角和弧角对Leksell-G系统手术的靶点误差有明显影响(P值分别为0.032、0.007)。其原因可能是由于Leksell-G系统由直角坐标系统与极坐标系统两部分组成，直角坐标系统采用笛卡尔坐标原理为基础，通过三个相互垂直的基准平面与三条基准线，确定靶点的空间坐标值。而极坐标系统以靶点坐标为球心利用弧形弓架在空间中形成一个球形空间，理论上任意的环角和弧角通过穿刺针均能够准确地到达靶点(穿刺针即球形坐标的半径)。然而同样是由于系统各部件之间存在着一定的活动幅度，穿刺路径的环角、弧角与水平面夹角越小时受到重力影响越大，故对靶点误差影响越明显。

综上所述，本研究通过颅骨标本，设置模拟靶点，模拟立体定向手术，直视下对靶点误差进行测量。通过实验获得Leksel-G手术方法的靶点误差，并对影响靶点误差的可能因素进行分析，得出相关结果。这些结果使得在临床工作中，并对可能影响靶点准确性的影响因素进行术前评估，使立体定向技术更好的为临床服务。