基于改进蝙蝠算法的梯级水库发电优化调度
张佳丹 顾圣平 郑斯水 唐凤珍


摘 要:针对梯级水库优化调度高维度、多约束以及非线性优化的特点,将自适应权重以及连续禁忌搜索算法引入标准蝙蝠算法,改善标准蝙蝠算法在水库优化调度应用中出现的早熟收敛且陷入局部最优的问題:一方面利用自适应权重避免因更新步长机制导致寻优能力不足的问题;另一方面利用连续禁忌搜索算法避免因种群多样性差导致陷入局部最优的问题。案例分析结果表明,改进蝙蝠算法能有效运用于水库发电优化调度中,并且与标准蝙蝠算法相比,具有更强全局寻优能力、更高的运行效率,得到的运行调度结果更优。
关键词:水库优化调度;蝙蝠算法;自适应权重;连续禁忌搜索算法
中图分类号:TV697.1文献标志码:A
doi:10.3969/j.issn.1000-1379.2020.06.011
Optimal Operation of Cascade Hydropower Station Reservoirs Based on the Improved Bat Algorithm
ZHANG Jiadan, GU Shengping, ZHENG Sishui, TANG Fengzhen
(College of Water Conservancy and Hydropower Engineering, Hohai University, Nanjing 210098, China)
Abstract:For the optimal operation of cascade reservoirs having the characteristics of high-dimension, multi-constraint and nonlinear optimization, the adaptive weight and continuous tabu search were introduced into the basic bat algorithm to solve the issue of premature convergence and getting the local optimal result easily in the optimal operation: On the one hand, the adaptive weight was used for avoiding the lack of optimizing ability caused by the step update mechanism; on the other hand, continuous tabu search was used for avoiding getting the local optimal result caused by the decline in population diversity. The case analysis shows that the improved bat algorithm can be effectively applied to the optimal operation of reservoir power generation and compared with the basic bat algorithm, it has stronger global optimization ability, higher operation performance and better operation scheduling scheme.
Key words: optimal operation; bat algorithm; adaptive weight; continuous tabu search
水库优化调度作为一个典型的非线性优化问题,能根据径流资料以及综合利用要求,运用优化方法寻求最优的水库调度方案,使水库在调度周期内经济效益最高,提高水能资源利用效率。然而,决策过程的多阶段性以及径流的不确定性使得水库优化调度求解难度较高且求解精度较低。传统的水库优化调度方法主要有动态规划算法[1]、逐步寻优算法[2]等,然而随着水库调度计算时段的细分,容易出现“维数灾”、耗时长的问题。近年来,粒子群算法[3]、遗传算法[4]等智能算法的出现使水库优化调度进入一个新阶段,但这些算法不可避免地出现鲁棒性差、寻优精度不高等问题。蝙蝠算法[5]是Xin-She Yang基于微型蝙蝠的回声定位行为于2010年提出的一种启发式算法,该算法结合了粒子群算法的学习机制以及模拟退火算法的冷却原理等,在计算精度、稳定性上优于其他算法,具有很好的发展潜力;与此同时,蝙蝠算法仍然会出现早熟收敛、陷入局部最优的问题。自适应权重[6]能够根据蝙蝠当前的离散程度与种群进化程度,动态地调整位置,从而保证最优解不易丢失;连续禁忌搜索算法[7]作为一种亚启发式算法,具有很强的局部搜索能力,能通过对一个初始可行解展开邻域搜索,并利用一种灵活的记忆结构以及相应的规则指导算法进行,避免出现迂回搜索从而陷入局部最优的情况。笔者尝试在种群更新机制中引入自适应惯性权重,并根据种群多样性的优劣[8]结合连续禁忌搜索策略对蝙蝠算法进行改进,以提高算法在水库优化调度中的全局寻优能力。
1 水库发电优化调度模型
电站运行效益的提高主要依靠发电量,因此可以在满足水电站的水位、水量以及出力等约束条件下,根据水库初始运行条件和入库径流,合理控制各个时段的发电流量,使得梯级电站在调度周期内发电量最大。
1.1 目标函数
以各个时段初的水位作为决策变量,建立发电量最大的目标函数。
F=max∑nk=1∑Tt=1KkQk,tHk,tΔt(1)
式中:n为梯级水库的个数;T为调度时段总数;Kk为水库k电站综合出力系数;Qk,t为水库k在t时段发电流量,m3/s;Hk,t为水库k在t时段发电水头,m;Δt为时段长度,h。
1.2 約束条件
(1)水量平衡约束:
Vk,t+1=Vk,t+(Ik,t-Qk,t-Sk,t)Δt(2)
(2)水位约束:
Zk,tmin≤Zk,t≤Zk,tmax(3)
(3)水库下泄流量约束:
Qk,tmin≤Qk,t+Sk,t≤Qk,tmax(4)
(4)水电站出力约束:
Nk,tmin≤Nk,t≤Nk,tmax(5)
式中:Vk,t为水库k在t时段初水库库容,m3;Ik,t为水库k在t时段入库流量,m3/s;Sk,t为水库k在t时段弃水流量,m3/s;Zk,t为水库k在t时段初的水位,m;Nk,t为水库k在t段电站出力,kW;Zk,tmin、Zk,tmax分别为水库k在t时段允许水位上、下限,m;Qk,tmin、Qk,tmax分别为水库k在t时段允许下泄流量上、下限,m3/s;Nk,tmin、Nk,tmax分别为水库k在t时段允许电站出力上、下限,kW。
2 改进蝙蝠算法
2.1 标准蝙蝠算法
蝙蝠算法是模拟蝙蝠利用回声定位原理来捕获猎物行为的一种启发式算法。假定优化问题为max F(X),蝙蝠随机分布在d维搜索空间中,每只蝙蝠的位置代表函数F(X)的一个解,对应的函数值即为蝙蝠的适应度值,适应度值越大则表示蝙蝠的位置越优。同时,蝙蝠飞行的过程代表解朝着更优方向更新的过程,每只蝙蝠可利用自己所发出的脉冲频率以及自身与当前最优位置的距离来调整飞行速度;蝙蝠的脉冲频率通过在[fmin,fmax]中随机分配获得,这个范围可根据所研究问题的具体情况进行设定,一般取[0,2]。那么,第i只蝙蝠发出的脉冲频率为fi,在g时刻的位置为Xgi并以速度vgi飞行,根据式(6)~式(8)在g+1时刻获得新的位置Xg+1i和速度vg+1i。
fi=fmin+(fmax-fmin)β(6)
vg+1i=vgi+(Xgi-X*)fi(7)
Xg+1i=Xgi+vg+1i(8)
式中:fmin、fmax分别为蝙蝠所发出声波的最大频率、最小频率;β为区间[0,1]内的一个随机数;X*为当前最优位置。
一旦蝙蝠的最优位置被选中,蝙蝠就按照式(9)在原先最优位置Xold附近以随机游走的方式生成一个新位置Xnew。
Xnew=Xold+εAg(9)
式中:ε为区间(-1,1)内的一个随机数;Ag为g时刻所有的蝙蝠发出脉冲响度Agi的平均值。
蝙蝠最初会以较小的脉冲发射速率和较大的脉冲响度来搜寻猎物,以保证有足够的搜索范围;在靠近猎物的过程中为能对猎物进行更精细地搜索,会降低发出的脉冲响度和提高脉冲发射速率。每只蝙蝠的初始脉冲响度A0i与初始脉冲发射速率r0i可以根据具体问题进行设定,一般取A0i=1表示蝙蝠发出的响度最大,r0i取接近于0的常数。若第i只蝙蝠在g时刻随机游走后最优蝙蝠位置得到改善并且发出的响度大于随机响度,则将蝙蝠当前最优位置更新为Xnew,其脉冲响度以及脉冲发射速率分别按照式(10)、式(11)进行更新;否则保持最优位置、脉冲响度以及脉冲发射速率不变。
Ag+1i=αAgi(10)
rg+1i=r0i[1-exp(-γg)](11)
式中:Ag+1i为第i只蝙蝠在g+1时刻的脉冲响度;rg+1i为第i只蝙蝠在g+1时刻的脉冲发射速率;α为声波衰减系数,一般取0.9;γ为脉冲速率增强系数,一般取0.9。
当迭代次数达到最大值G时,蝙蝠位置停止更新,并输出蝙蝠的最优位置作为本次计算的最优解。
2.2 算法的改进
2.2.1 自适应权重
在标准蝙蝠算法中,一旦蝙蝠以某种频率发出超声波后,其速度的更新主要依靠当前全局最优位置,步长变化过于单一,容易丢失最优解,从而影响蝙蝠算法的搜索性能。在速度更新公式中引入自适应惯性权重,可以根据蝙蝠当前进化程度以及离散程度,动态改变蝙蝠的更新速度,平衡算法的全局搜索与局部开发能力。对于整个种群来说:进化初期应分配较大的惯性权重以保证全局搜索性能,在进化后期应分配较小的惯性权重以保证算法的收敛性能。对于蝙蝠个体来说:个体适应度差于整个种群的平均适应度时,应提高寻优速度,分配其较大的惯性权重;个体适应度优于整个种群的平均适应度时,应提高局部开发能力,分配其较小的惯性权重。改进的速度更新公式如下:
vgi=wgivg-1i+(xgi-x*)fi(12)
wgi=wmax-(wmax-wmin)[g2G+Fgmax-Fgi2(Fgmax-Fgavg)],
Fgi≥Fgavgwmax,Fgi
式中:wgi为第i只蝙蝠在g时刻的惯性权重;wmax、wmin分别为惯性权重的最大值、最小值;Fgi为第i只蝙蝠在g时刻的适应度值;Fgmax为种群内所有蝙蝠在g时刻的最优适应度;Fgavg为种群内所有蝙蝠在g时刻的平均适应度值。
2.2.2 连续禁忌搜索算法
随着迭代次数的增加,蝙蝠个体会不断靠近当前最优位置而导致种群多样性急速下降,使得寻优能力变差。连续禁忌搜索算法是禁忌搜索算法在连续优化问题上的一种拓展,是通过模仿人类寻找东西行为的亚启发式算法:在一段时间内不会对已经搜寻过的地方进行重复搜索;若没有找到,则回到原来的地方继续寻找。在蝙蝠算法后期已经得到相对较优解的情况下,可引入连续禁忌搜索算法来进一步提高寻优精度:从蝙蝠搜索到的最优解为中心点(即X*)出发展开邻域搜索,对于已搜索到的局部解进行标记和筛选,并在接下来的若干次迭代中避开这些解,从而能保证对解的不同区域的有效搜索。
连续禁忌搜索算法有以下几个重要因素:
(1)邻域。假定当前的邻域中心点为d维变量X,分别以各个分量xj为中心绘制w个同心超矩形,并在每个同心矩形He(e=1,2,…,w)内随机选取1个点以及在中心矩形H0内随机选取s个点,由这w+s个点共同组成X的邻域;一般情况下,取w=5,s=3。同心超矩形数学定义如下:
H0(x,h0)={x′||xj′-xj|
xj′
(14)
He(x,he-1,he)={x′|he-1<|xj′-xj|
xjmin
he=2he-1(16)
h0=0.001(xjmax-xjmin)(17)
式中:xjmax、xjmin分别为分量xj的最大值、最小值;he为同心矩形He领域半径;h0为中心矩形H0的领域半径。
(2)禁忌表和禁忌规则。在连续禁忌搜索算法中,将需要避开的解称为禁忌对象,换句话说,这些解处于被禁忌的状态;禁忌表则是用来存储禁忌对象的结构,禁忌表能存放禁忌对象的最大个数称为禁忌长度。算法运行初始,建立一个空的禁忌表,禁忌长度为L,第一个邻域中心点X*直接放进禁忌表中。
每次迭代都采用两重禁忌规则来判定邻域中的点X′在本次迭代中是否被禁忌。首先判断适应度值F(X):若X′与任意禁忌对象Xl(l=1,2,…,L)的关系均满足式(18),则X′没有被禁忌;否则表示X′的适应度值接近于某个禁忌对象X′l,判断这两个点是否接近,若此时对于任意的分量xj(j=1,2,…,d),均满足式(19),则点X′被禁忌,否则没有被禁忌。
|F(X)-F(X′l)|≥εf1(18)
|xj-xj′l|≤εf2(19)
式中:εf1、εf2均为常数,一般取0.001;L为禁忌长度,一般取常数。
如果X′没有被禁忌,则按照“先进先出”原则放置在禁忌表中,并将下一次迭代的邻域中心点Xnow更新为X′;当禁忌个数超过禁忌长度时,将最早进入的禁忌对象剔除。如果X′被禁忌,則不把X′放进禁忌表中,并将X′从邻域中剔除,从剩余邻域中选取一个最优解,再次进行禁忌判断,直到找到一个解X″没有被禁忌。
(3)特赦规则。为保证算法的优化效果,避免因禁忌规则而导致算法出错,还需要设置特赦规则:当解X′优于当前最优解Xbest时,为保证解X′不会因禁忌规则而被漏掉,更新当前最优解Xbest后,无视禁忌规则直接判定X′没有被禁忌;当邻域内所有解都没有优于当前最优解Xbest且都被禁忌,为防止算法出现死循环,将禁忌表内的所有禁忌对象取线性平均值,直接判定没有被禁忌。
(4)终止规则。迭代步数达到最大值,则终止迭代,输出最优解。
除上述几个因素外,还要考虑进行禁忌搜索的合适时机:若过早进行禁忌搜索则干扰到蝙蝠的寻优过程;若太晚进行禁忌搜索,则会影响最终的寻优效果。因此,可以设定一个阀值ξ,对蝙蝠的种群多样性进行判断。种群在第g时刻的相对多样性公式如下:
ξ(g)=div(g)div(0)
div(g)= 1md∑dj=1∑mi=1[xji(g)-x*j(g)UBji-LBji]2(20)
式中:xji(g)为第i只蝙蝠在g时刻的第j个分量;x*j(g)为最优位置X*蝙蝠在g时刻的第j个分量;UBji、LBji分别为分量xji(g)的最大值和最小值。
当ξ(g)小于ξ时,表明蝙蝠的种群多样性比较差,此时,选取最优蝙蝠个体作为进行禁忌搜索的初始点展开进一步寻优。
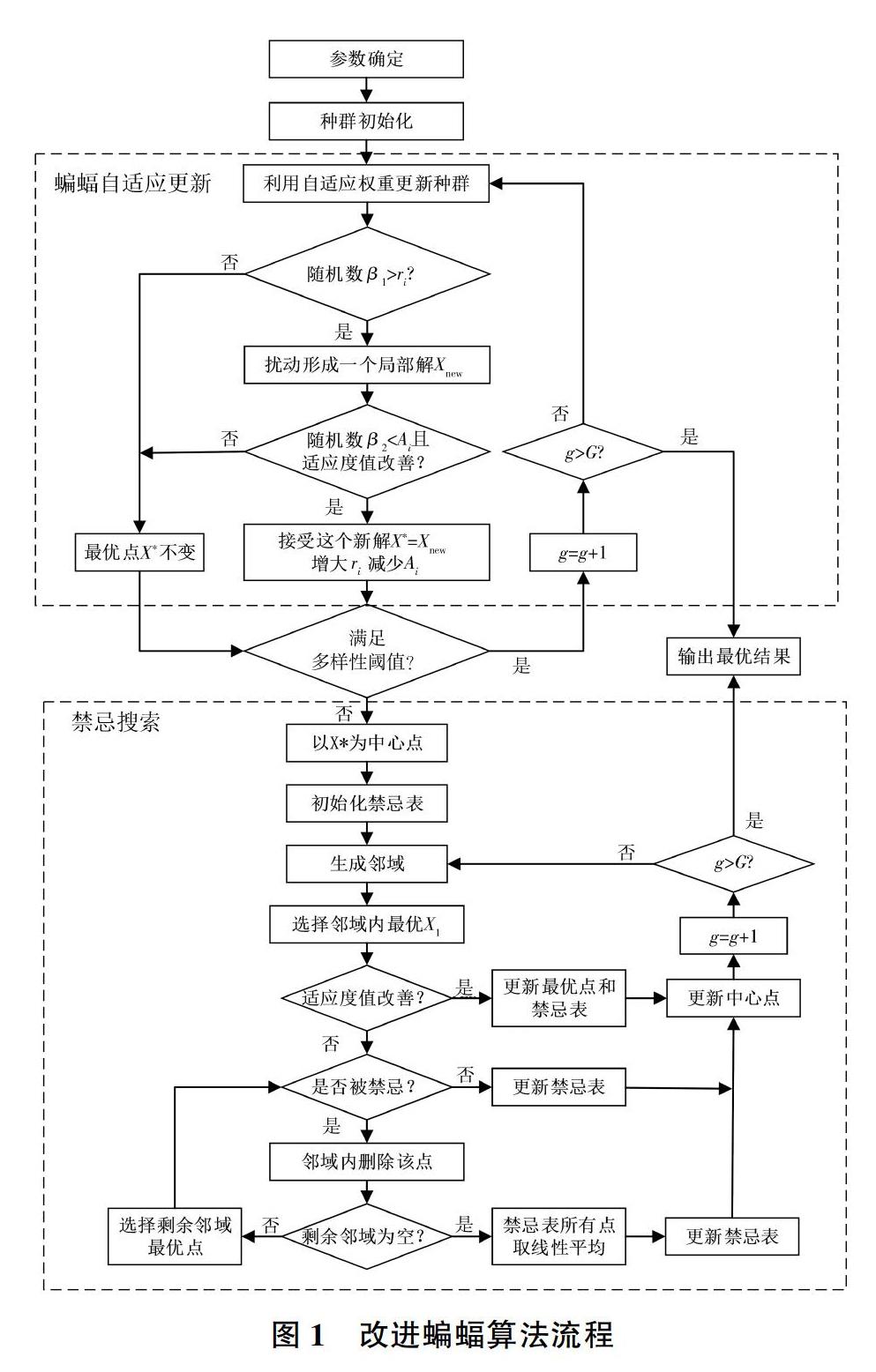
2.3 改进蝙蝠算法计算流程
在处理水库优化调度中的约束条件时,水库各时段的运行水位约束通过限制蝙蝠的位置范围来实现,而其他约束则引用罚函数概念处理。改进的蝙蝠算法求解水库优化调度问题的主要步骤如下:
第一步:确定参数。蝙蝠的种群规模m,脉冲频率范围[fmin,fmax],初始脉冲响度A0,初始脉冲发射速率r0,最大迭代次数G,种群多样性阈值ξ,禁忌搜索的禁忌长度L。
第二步:种群初始化。生成m个可行解作为每只蝙蝠的初始位置X0,计算每只蝙蝠适应度F(Xi),选择当前的最优位置X*。
第三步:种群迭代。按照式(6)、式(8)、式(12)和式(13)对蝙蝠的位置和飞行速度进行自适应更新,并更新当前最优位置X*。
第四步:局部搜索。选择最优的蝙蝠位置并生成一个随机数β1。如果ri小于β1,则按照式(9)在附近进行扰动形成一个局部解,并进行下一步判断;否则,跳到第六步。
第五步:更新最优位置。生成另一个随机数β2,如果最优位置得到改善并且Ai大于β2,则更新蝙蝠的最优位置,并按照式(10)、式(11)调整蝙蝠的脉冲响度和脉冲发射速率;否则,保持不变。
第六步:种群多样性判断。当前蝙蝠多样性若满足阈值要求,则进行第七步;否则,跳到第八步。
第七步:如果迭代次数达到最大,则输出最优结果;否则,回到第三步。
第八步:禁忌搜索。从当前最优解X*出发进行连续禁忌搜索,根据禁忌规则以及特赦规则,更新禁忌表、邻域以及当前最优解。
第九步:如果迭代次数达到最大,则输出最优结果;否则,回到第八步。
改进后的蝙蝠算法流程图见图1。
3 实例应用
我国某梯级系统上游至下游包含2个水电站A、B,两个电站均以发电为主要任务,电站间有区间入流汇入。电站的基本参数见表1。
由于2个电站在汛期基本保持在汛限水位运行,因此针对供水期进行优化调度分析。选用梯级电站系统3个典型年供水期(12月至次年5月,共6个月)的径流资料,以旬为计算时段,分析梯级水库的发电优化调度结果。
设置蝙蝠种群大小m=100,蝙蝠发出的脉冲频率范围[fmin,fmax]为[0,2],初始脉冲响度A0=1,初始脉冲速率r0=0.001,声波衰减系数α=0.9,脉冲速率增强系数γ=0.9;在改进蝙蝠算法中最大惯性权重wmax=1,最小惯性权重wmin=0.4,种群相对多样性阈值ξ取0.001,禁忌搜索的禁忌长度L=6。标准蝙蝠算法和改进蝙蝠算法计算得到的梯级总发电量优化结果见表2,相应的3个典型年供水期的水库A、B优化调度水位过程如图2~图4所示。
由以上结果可知,改进蝙蝠算法比标准蝙蝠算法计算得到的梯级发电量有所增加,枯水年增加1.90×106 kW·h,平水年增加9.57×105 kW·h,丰水年增加1.15×105 kW·h。表明从梯级发电量考虑,改进蝙蝠算法的优化效果更好。
为了进一步比较这两种优化算法的收敛速度,这里以枯水年供水期计算为例,给出两种算法的迭代过程,如图5所示。
由图5可知,标准蝙蝠算法达到收敛所需迭代次数大于改进蝙蝠算法所需迭代次数,表明改进蝙蝠算法在获得更优解的前提下,收斂速度明显提高。
4 结 论
在标准蝙蝠算法中引入自适应权重,改善蝙蝠种群的更新机制,使蝙蝠位置能够根据实际情况进行自适应动态调整,提高蝙蝠的搜索性能;同时,在算法后期种群多样性变差时,引入连续禁忌搜索算法,避免出现迂回搜索而无法跳出局部最优的情况。案例分析表明,改进蝙蝠算法与标准蝙蝠算法相比,能以较快的运行效率获得更优的水库运行方案,为水库发电优化调度提供了一个新的途径。
参考文献:
[1] 杨峰,黄怀礼,张强.用动态规划法对水库进行优化调度[J].河南科学,2005,23(1):17-19.
[2] 罗红兵.POA算法在水库优化调度中的应用[J].陕西水利,2018(6):127-129.
[3] 邓显羽,彭勇,叶碎高,等.粒子群算法在水库(群)优化调度研究中的应用综述[J].水利水电科技进展,2010,30(5):90-94.
[4] 冯迅,王金文,权先璋,等.遗传算法在水电站优化调度中的实用研究[J].华中电力,2005(3):12-15.
[5] YANG X S. A New Metaheuristic Bat-inspired Algorithm[J].Computer Knowledge &Technology,2010,284:65-74.
[6] 刘列.自适应粒子群算法在水库优化调度中的应用研究[J].大众科技,2017,19(1):11-13.
[7] 王明兴.连续禁忌搜索算法改进及应用研究[D].杭州:浙江大学,2005:15-27.
[8] 纪昌明,刘方,喻杉,等.基于鲶鱼效应粒子群算法的梯级水库群优化调度[J].电力系统保护与控制,2011,39(19):63-68.
【责任编辑 崔潇菡】

