基于Memetic算法的闭环物流网络模糊规划模型

张 鑫，赵 刚，齐颖秀,李伯棠

(1.上海海事大学 交通运输学院，上海 201306；2.北京交通大学 交通运输学院，北京 100044；3.广州航海学院 港口与航运管理学院，广东 广州 510330)

0 引言

出于对环境保护的考虑，如何通过再利用和再制造来减少物料使用已成为企业关注的重要问题。结合绿色供应链管理的思想，可以引导出闭环供应链管理的问题。不同于传统的供应链，设计绿色供应链要求有再循环的功能，因此拥有闭环链式的物流网络是物料流所需的基础结构。同时，通过对逆向物流进行科学管理,采用3R(即减少原料(Reduce)、再利用(Reuse)和再循环(Recycle))的思想指导相关流程，能够延长产品使用寿命，节约生产成本，保护自然环境[1]。闭环物流包括正向物流和逆向物流两部分。对于作为传统物流的正向物流来说，产品在制造工厂和配送中心经过处理之后，最终被送到客户，以满足他们的需求。因此，客户点是正向物流过程的终点。对于逆向物流，废旧产品从客户点返回到拆解中心，通过分类或拆解进行修复、再利用或填埋处置[2-4]。闭环物流管理遵循物料生命周期守恒的原理以保证最小的物料损耗。

网络规划是影响物流企业战略决策的重要问题，其中：设施选址和线路选择会显著影响网络的运营成本，且开放或关闭一个设施既昂贵又耗时，也很难在短期内改变网络结构，这使得物流网络规划成为企业战略层决策的一个重要问题[5]，而规划合理的闭环物流网络是解决问题的关键。

现实生活生产存在的不确定性会影响物流网络的运作，进而增加企业的风险。在处理物流网络的不确定性问题中，大部分文献采用的随机规划理论需要依靠以往积累的数据[6-7]，但是生产经营过程的复杂性和产品生命周期的短暂性问题使得数据难以获取，因此在应用过程中存在难度[8]。鉴于上述问题，少数文献采用模糊数学规划，这种方法可以不依赖以往积累的数据来解决不确定性问题[9-10]。

带有选址的物流网络问题是一个NP-hard问题[11-13]。有效的解决方法对于研究人员来说仍然是一个挑战。遗传算法(Genetic Algorithm, GA)是一种基于自然选择和自然遗传机制的随机搜索方法[14]。GA作为一种进化的方法，一直受到人们的关注，并成功地应用于组合优化问题[15]。传统的GA局部搜索能力不强，容易陷入“早熟”。Moscato等[16]首次通过在GA中整合邻域搜索，提出Memetic算法(Memetic Algorithm, MA)的概念，以增强搜索的强度。MA通过增加邻域搜索被证明可以成功应用在各种优化问题中，特别是可以求出NP-hard优化问题的近似解[17]。MA结合领域的知识和基于群体的搜索方法(如GA)，具有高效启发式算法的特点，已被应用于多种优化问题，如生产分配问题[18]、调度问题[19]、最小跨度频率分配问题[20]和划分问题[21]。

对于MA中解的表示问题，Choudhary等[22]利用基于节点深度等级的生成树编码方法，但是该方法可能会生成不可行解，导致需要进行编码修复。文献[13,23-26]都利用了一种不需修复机制的基于优先级编码的方法，然而该编码方法会使算法过于早熟，陷入局部优化解而错失全局优化解。因此，本文利用双层优先级编码(编码过程见4.1节)的方法使算法进行更加全面的全局和局部搜索，提高算法的效率。

同时，MA的一个重要目的是使算法能够进行更有效的邻域搜索。Fung等[27]利用一个带有2-opt、1-1交换移动和1-0交换移动这3种邻域搜索的MA解决开弧路径问题。Karaoglan等[28]使用模拟退火(Simulated Annealing, SA)和整数规划公式(Integer Programming Formulation, IPF)相结合的邻域搜索，提出一个解决带有选址和路径选择的配送网络问题的Memetic算法。Hasani等[29]采用基于禁忌列表的自定义混合自适应大邻域搜索算法进行邻域搜索，并提出一种基于Taguchi高效并行的MA以解决全球供应链网络设计问题。然而，以上方法只是运用一种或简单地叠加两种以上的邻域搜索，从而使得求解效率不高。因此，本文采用一个动态的邻域搜索方法将2-opt和3-opt两种方法有机结合在一起，从而提高算法的局部搜索效率。

综上所述，本文将探究模糊环境下的闭环物流网络设计问题，构建基于可信性的闭环物流网络模糊规划模型，并采用一种带有动态邻域搜索和基于双层优先级编码的Memetic算法(Bi-level Priority-based encoding Memetic Algorithm with dynamic local search, BPMA)对模型进行求解，然后将BPMA与LINGO的求解结果进行对比，并对构造的闭环物流网络进行分析。

1 问题描述

本文考虑的闭环物流网络由正向物流和逆向物流组成(如图1所示，图中每个图形包含一个或一个以上的设施)，包括工厂、配送中心、拆解/分类中心、收集中心、再利用中心和顾客点。顾客认为不满意或用旧的成品进入逆向物流，收集中心回收这些产品并将产品送到拆解/分类中心进行检验，能够再利用的产品送到再利用中心，需要再制造的产品运到工厂。产品经过工厂的再制造和再利用中心的处理进入正向物流，新产品和再利用产品运输到配送中心，配送中心负责将产品运到顾客手中。其中，在拆解/分类中心和再利用中心处理产品时，产生的不能进行处理而废弃的产品就地填埋。

实际生产中，各种不确定因素的存在干扰了企业管理者对市场变化的准确把握。为此，本文假定某些参数具有不确定性，并采用梯度模糊数表示参数的变化。

在上述条件下，本文针对单位运输成本、设施能力、回收率和需求等不确定参数，将网络中生产、运输、固定运营和填埋等的总成本最小化作为目标，进行闭环物流网络中各设施选址以及设施间运输线路的选择，并运用模糊数学的可信性理论，构建闭环物流网络模糊规划模型，对网络进行研究。

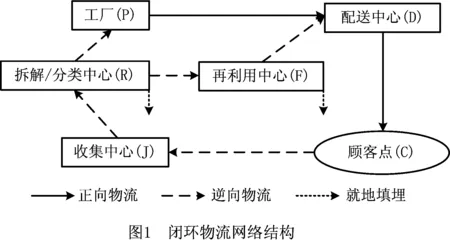
2 模型的建立

2.1 模型假设与符号说明

本文作如下假设：①考虑单个生产周期内的单种类产品；②设施数量和处理能力有限；③产品拆解过程中和产品再利用过程中的浪费比率均确定；④顾客区域既能回收产品，又对再利用产品有购买力。基于建模的需要，定义符号如表1～表3所示。

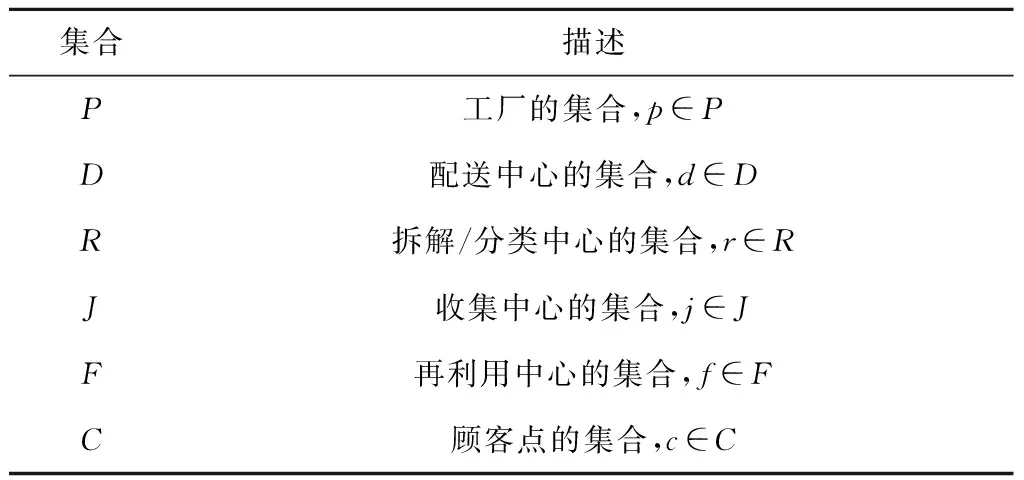
表1 模型中集合的定义

表2 模型的参数

续表2

表3 模型的决策变量

2.2 目标函数与约束条件

本文研究的闭环物流网络设计问题含有模糊参数，因此建立一种基于可信性的模糊规划模型[30-31]，将期望值方法(用于目标函数)和机会约束规划方法(用于约束条件)相结合进行建模。因此，可得到基于可信性的模糊机会约束规划模型M1。

模型M1的目标是使总成本(TC)最小，根据问题描述，其由设施建设成本(TSC)、设施开设的固定成本(TFC)、运营成本(TPC)、收购成本(TPUC)和运输成本(TTC)组成。其中：TPC指中心处理产品的成本，包括拆解/分类中心和再利用中心处理浪费产品的成本；TPUC指回收旧产品的购买成本；TTC指节点间的运输成本。因此，目标函数表示为:

minE[TC]=E[TSC]+E[TFC]+E[TPC]+

E[TPUC]+E[TTC]。

(1)

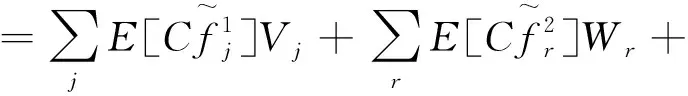
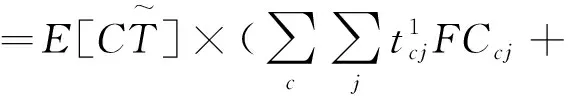
根据模型假设条件，目标函数的决策变量需满足以下约束条件：

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

Vj,Wr,Xf,Yp,Zd∈{0,1},

∀j∈J,r∈R,f∈F,p∈P,d∈D；

(16)

FDdc,FNdc,FCcj,FJjr,FRrf,FTrp,FFfd,FPpd≥0,

∀p∈P,d∈D,r∈R,j∈J,f∈F,c∈C。

(17)

其中：

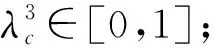
(4)其他约束 式(16)为0-1变量约束；式(17)为非负整数约束。

3 模型的分析处理

(18)

(19)

(20)

(21)

根据式(20)和式(21)，有如下定理：

(22)

(23)

由式(22)、式(23)和梯形模糊数的期望值，可以将模型M1转化为M2(清晰等价模型)：

minE[TC]=E[TSC]+E[TFC]+E[TPC]+

E[TPUC]+E[TTC]。

(24)

[(γ(1)+γ(2)+γ(3)+

E[TPUC]=[(PE(1)+PE(2)+PE(3)+

E[TTC]=[CT(1)+CT(2)+CT(3)+CT(4)]×

s.t.

(25)

(26)

∀c∈C；

(27)

∀c∈C；

(28)

j∈J；

(29)

∀r∈R；

(30)

(31)

∀p∈P；

(32)

∀f∈F;

(33)

式(2)，式(5)～(8)和式(16)～(17)。

4 求解方法

第3章所建模糊规划模型M2，对于小规模的问题可以用LINGO、CPLEX等软件求解，但是当问题的规模变大时，现存求解软件的效率较低，需用启发式算法(如GA、MA和蚁群算法等)求解。因此，本文采用MA对模型进行求解，并将求解结果与LINGO的求解结果进行对比分析。

根据文献[15-20]可知，Memetic算法是一种建立在模拟文化(也称文化基因，即问题的一个可行解)群进化基础上的优化算法，其主要步骤包括：

(1)初始种群的产生，初始种群一般是随机产生的；

(2)进化操作，可以采用遗传算法中的交叉、变异算子中的一个或两个；

(3)局部搜索，是推举局部区域优秀个体的过程；

(4)新种群的产生，经过前两个步骤后种群数目通常大于初始数目，此时需要通过一定的机制(如轮盘赌选择)选出较优的种群。根据MA的主要步骤并结合本文的问题，下面给出本文BPMA算法的步骤如下：

步骤1初始化。根据文化基因的个体编码结构随机生成2×(pop_size)个文化基因。

步骤2计算各个体的适应度。运用后文算法2得到的结果求出每个个体的适应度值。

步骤3选择操作。

步骤4交叉操作。

步骤5动态邻域搜索。

步骤6结束。判断当前迭代数是否超过最大迭代数，如果是则输出优化值，否则返回步骤2。

4.1 文化基因的个体编码结构

对于运输问题，其解的结构包括起点|K|(可理解为供应点、仓库等)和终点|L|(可理解为需求点)，这样可以得到一个|K|行|L|列的运输矩阵，而在这样的运输矩阵里，需要确定优先满足哪一个终点，以及确定优先由哪一个起点满足该终点。通过参考文献[22-25]的编码方法和根据本文问题的特征，本文提出一个双层优先级的个体编码方法。第一层优先级是终点的优先级数(如表4中的第3行)，第二层是运输矩阵的优先级数(如表4中的第4行)。通过运用模型M2的决策变量符号，首先按照FDdc,FNdc,FPpd,FFfd,FRrf,FTrp,FJjr,FCcj的顺序随机生成一个如表4中第3，4行的两层优先级数(表5为以FDdc为例的第二层基因，表示一个3行4列的矩阵)。

表4 一个闭环物流网络模型基因的实例说明

表5 一个第二层闭环物流网络模型基因的实例说明

如表4所示，随机生成如第3行各节运输矩阵终点的优先级数。此外，如表5所示，生成|D|行|C|列的矩阵，并随机填入[1,|D|×|C|]范围内不同的整数，构成了zkl的第二层基因，其中：|D|表示出发点的数量，|C|表示到达点的数量(同理，FDdc,FNdc,FPpd,FFfd,FRrf,FTrp,FJjr,FCcj也是按此随机生成)。

4.2 文化基因的解码算法

算法的解码方法是以算法2的数据输入开始，利用算法1求出各设施之间的运量，即相当于求出模型M2的决策变量，并用于计算目标函数和适应度的值。

算法1双层优先级的解码方法。

输出:xkj为节点k到节点j的运输量。

步骤1 xkj,∀k∈K,j∈J

步骤3 xk*j*=min{ak*,bj*}

更新需求量和能力:ak*=ak*-Xk*j*,bj*=bj*-Xk*j*

else返回步骤2

End

注：本节符号与模型符相互独立，只为说明文化基因解码流程。

上述算法过程的具体说明如表6所示(以表4第1节的优先级与表5的优先级为例)。

表6 解码过程跟踪表

算法2模型M2个体的解码算法。

输出:FDdc,FNdc,FPpd,FFfd,FRrf,FTrp,FJjr,FCcj。

步骤1 使用算法1计算FDdc。

步骤2 使用算法1计算FNdc。

步骤3 使用算法1计算FPpd。

步骤4 使用算法1计算FFfd。

步骤5 使用算法1计算FRrf。

步骤6 使用算法1计算FTrp。

步骤7 使用算法1计算FJjr。

步骤8 使用算法1计算FCcj。

4.3 适应度与选择操作

在MA的种群中，每个文化基因都需要通过计算其适应度来进行评估。适应度函数表示各个文化基因的优缺点。本文的适应度为目标函数值(由式(24)计算)的倒数。

选择操作采用轮盘选择法的方法。假设种群数量为pop_size个，由于MA中种群进行交叉操作后，种群数量变为原种群数的两倍，即2×pop_size个。因此，在选择操作进行时，轮盘需要转2×pop_size次，轮盘转两次选择出来的两个文化基因，根据其适应度值选择适应度值最好的文化基因，下两次重复同样的操作过程，以使种群数量保持在pop_size个。

4.4 交叉操作

采用两点交叉的方法：

(1)生成区间[1,8]内两个随机整数d1和d2，确定两个位置(即第d1、d2节)，对两个位置之间的数据进行交叉，如d1=2和d2=3时，操作过程如表7和表8所示。

表7 交叉操作执行前的染色体

表8 交叉操作执行后的染色体

(2)交叉后，利用中间段的对应关系进行映射，映射过程如下：例如上表第2行第4列的20和第10列的20重复，需要在交叉部分通过同列的对应关系找出不重复的数字，即20→18→15→1→2→13，因此第2行第4列的20变为13(在表9中用粗体标记)，表9中其他粗体的16、11和20可得：

表9 染色体映射修正过程

本操作不具有交叉概率，对于每两个父代的文化基因必须进行交叉，得到的两个子代文化基因需要根据其适应度值进行邻域搜索。

4.5 动态邻域搜索

交叉阶段产生的两个子代文化基因中，适应度值最好的文化基因会被选择进行邻域搜索，使其更优化。进行邻域搜索前，文化基因需要按一定概率(本文设计为70%)判断是否进行该操作。这里有2-opt和3-opt两种邻域搜索方法。邻域搜索的过程针对第二层优先级，其中2-opt的过程是：首先产生一个[1,8]区间内的随机整数r，然后在这第r节的第二层矩阵内随机选取两个数字，将其对换位置。同理，3-opt是在这第r节的第二层矩阵内随机选取3个数字，将其对换位置，使得3个数不在原来位置上。基于以上分析设计如下动态邻域搜索算法。

算法3动态邻域算法。

For i=1 to(10+k/8)

If i<4运用3-opt邻域搜索

Else运用2-opt邻域搜索

If所得邻域文化基因的适应度值比当前文化基因的适应度值好，则所得邻域文化基因替换当前文化基因

Else以(0.05*pw)的概率将当前文化基因替换为所得邻域文化基因

End

算法3中：k为当前迭代的数；pw=(tun-k)/(tun×3)，tun为总迭代数。

5 算例分析

为了评价第4章所提出的BPMA算法在闭环物流网络设计问题中的性能，将BPMA算法与文献[13]的pGA算法进行比较，因为pGA算法同样使用基于优先级编码的方法和应用在不确定规划中，但是使用不同的进化搜索策略。此外，M2模型也在LINGO11上编码和运行，BPMA算法也与求解器所得结果进行对比。BPMA和pGA运用软件MATLAB 7.0进行代码的编写，软件MATLAB 7.0和LINGO 11的运行环境为：处理器为Intel(R)Core(TM)i7 2.70 GHz，内存为4 GB，操作系统为Window10(64bit)的手提电脑。本文根据表2和表10随机生成7个规模不同的测试问题。

设定置信水平为1，BPMA算法的交叉率取60%，pGA算法的交叉率和变异率分别取60%和15%。两个算法对每个测试问题运行10次，得到如表11所示结果(加粗数字表示最优解，标记“*”的表示可行解)。并利用文献[13]的算例将BPMA算法和pGA算法进行对比(如表12)。为了对比双层优先级编码和pGA的编码，本文设置了BPGA算法，其中BPGA算法的选择操作与pGA一样，并沿用BPMA的交叉操作，变异操作按50%的概率采用2-opt和3-opt两种方式进行变异，最后利用BPGA和pGA对测试问题2进行求解得到如图2所示最优值曲线。

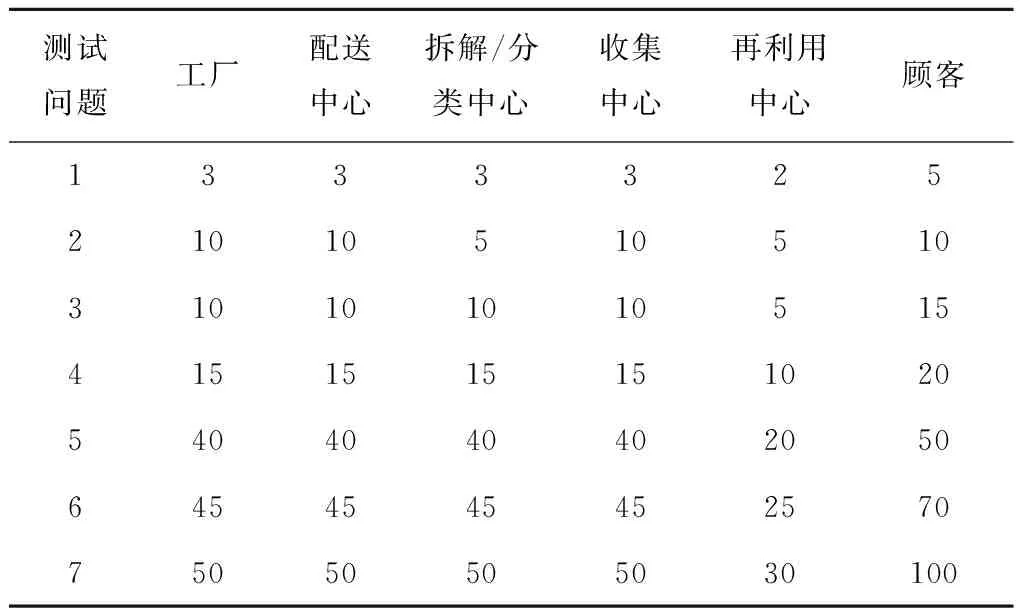
表10 测试问题的规模 个

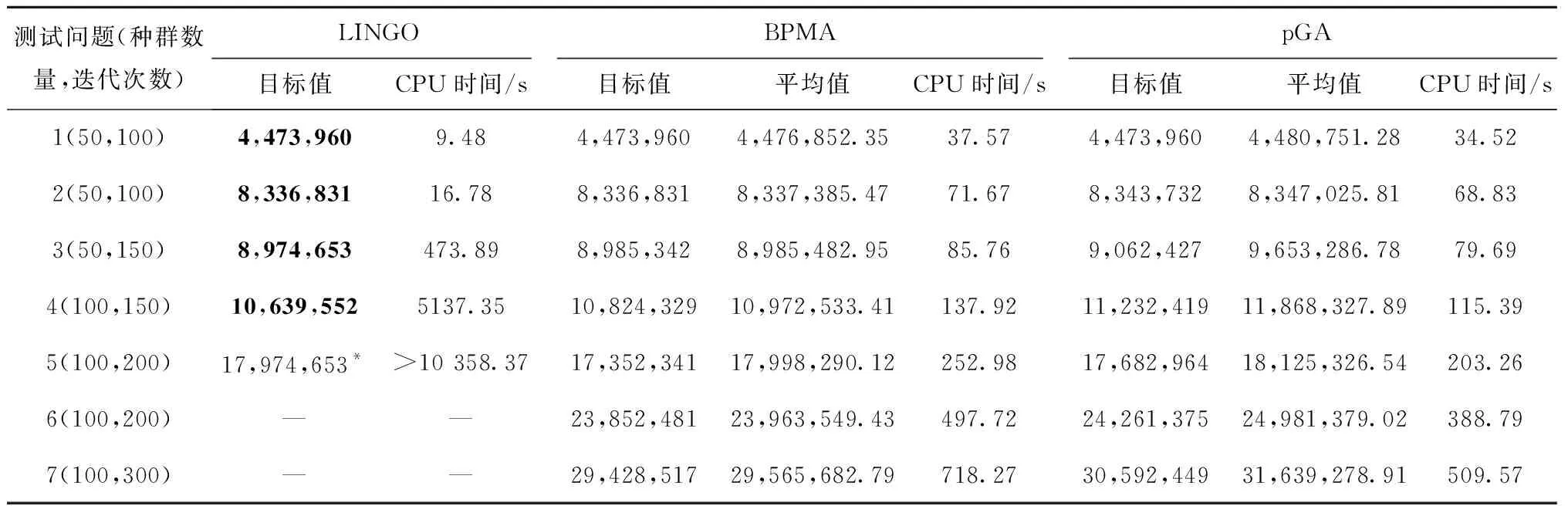
表11 运算结果

表12 BPMA与pGA运算结果的对比分析

从图2可以看出，在同样使用遗传算法时，相比于基于优先级编码方式，双层优先级编码方式的求解结果好,且更容易跳出局部优化解。由此证明，本文所提双层优先级编码方式具有一定的优势。

在表11中，对于测试问题1和2，两个方法所得目标函数值相同，但BPMA的运行时间比LINGO运行时间长，说明BPMA对小规模的问题是适用的，但是效率比LINGO低；对于测试问题3和4，使用BPMA求出的目标函数值比运用软件LINGO运算得到的目标函数值大，但是BPMA运行的时间比LINGO运行的时间短，说明虽然BPMA对中间规模的问题精度下降，但是其效率有所提高；对于测试问题5，使用BPMA求出来的目标函数值比运用软件LINGO运算得到的目标函数值小，且BPMA运行的时间比LINGO运行的时间短得多，还有对于测试问题6和7，软件LINGO未能提供可行的解决方案，与此同时，BPMA却可以在较短时间内提供较好的解决方案。由此证明，本文所提BPMA算法具有一定的效率。

由表11可以看出，BPMA算法与pGA算法相比，对于测试问题1和2，两个算法得到最好的目标值相同，对于测试问题3～7，BPMA得到的目标值比pGA小，但是对于全部测试问题，BPMA运行时间比pGA长，且随着问题规模增大，BPMA所用时间增加的速度越多，这是由BPMA的动态邻域搜索操作时花费较多时间所造成的，但是该过程可以帮助BPMA算法增加局部搜索的能力，从而得到较好的解。同样地，通过观察表12可知，BPMA得到的目标值比pGA更优，但是BPMA的求解时间比pGA长。因此，虽然BPMA算法比pGA算法运行时间长，但是BPMA求出解的质量高，说明BPMA算法具有一定的精度。

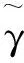
表13 设施的相关数据

表14 顾客点的需求数据

在表15中，网络变化的总趋势是：随着置信水平的降低，网络中的设施选址不同，且选定的设施总数量减少，目标值(成本)下降。这是因为置信水平的降低导致可信的需求量下降，并且允许不可信的需求(即对于是否购买物料或产品是不确定的)可以不满足，从而使网络中的物流量减少，令运输费用减少，同时减少设施的开设也能满足这部分物流量，使得设施的固定费用减少，最终让目标值下降。

表15 置信水平变化时的选址方案及目标函数值

再分析表15，对于置信水平为65%～100%时，解决方案是选择了收集中心1、2、3，拆解/分类中心1、2和3，配送中心2和3，工厂2和3，以及再利用中心2；对于置信水平为60%时，其解决方案与置信水平为65%～100%的解决方案相比，不同点是不选择收集中心2和拆解/分类中心1；对于置信水平为55%时，其解决方案和置信水平为60%的解决方案相比，不同点是不选择工厂2。但是，对于置信水平为50%时，解决方案是选择了收集中心1和2，拆解/分类中心1和2，配送中心1，工厂2和3，以及再利用中心1，其解决方案和置信水平为55%～100%的解决方案相比，不是纯粹地减少设施数量，而是选址发生改变。因此，以上分析说明置信水平对物流网络结构的影响是明显的。

通过观察图3，除了目标值(成本)随着置信水平的上升而增加之外，置信水平为65%～100%时置信水平与成本呈一种类似线性正比(即目标值增加的幅度相近)的关系，而置信水平为50%～65%时置信水平与成本是不成正比的，其中置信水平为50%～55%和60%～65%的目标值增幅较大，而置信水平为55%～60%的目标值增幅较小。由此说明，置信水平的变化对目标值的增加影响大，且其影响的增幅是不规律的，即置信水平的变化是具有风险性的。

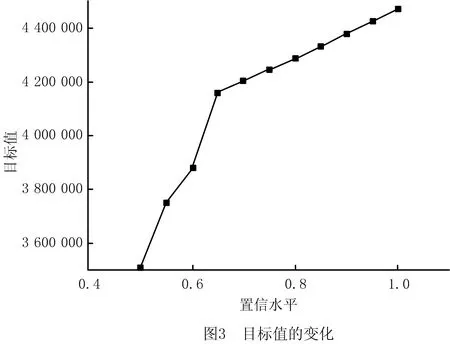
综上所述，置信水平的变化对于物流网络选址和节点间运输路线的影响是明显的，企业决策者需要根据顾客需求和其他相关信息的变化合理地选择参数的置信水平，从而得到更加合理可行的决策方案。

6 结束语

本文以闭环物流网络为研究对象，考虑参数的不确定性，建立了一个模糊混合线性规划模型，并提出一个带有动态邻域搜索和基于双层优先级编码的Memetic算法，最后通过算例证明了基于双层优先级编码方式以及应用该方式编码的Memetic算法的有效性和模型的适用性，所得结果为供应链管理者提供决策支持和方法指导。

一个具有良好形象的企业不仅要考虑经济因素，还要考虑企业运作时对环境的影响和承担相应的社会责任，因此下一步的研究工作是在考虑经济、社会和环境因素的基础上，更加全面地优化物流网络，以保证物流网络的可持续发展。