交通荷载作用下厚层老黏土动力特性研究

张树轩 陈立伟 杨为民 司海宝

(1. 中国核电工程有限公司，北京 100840；2. 中国地质科学院地质力学研究所，北京 100081；3.安徽工业大学，安徽马鞍山 243000)

0 引言

随着高速铁路技术的不断推广，城市间轨道交通发展愈发迅猛。为保证2022年冬奥会交通需求，国家修建由北京至张家口的高速铁路。近年来，高铁运行产生的交通荷载造成轨道不均匀沉降一直为国内外土动力学研究的热点问题之一。铁道部对无砟轨道的沉降变形提出明确要求[1]。通过土体动力特性研究可为高铁沉降变形计算提供理论依据，对高铁维护及安全运营具有重要意义。当前对土动力学特性的研究大多通过室内动力学试验开展。由于原状土试验结果存在离散性，多数学者对交通循环荷载试样的研究多选取重塑土作为试验对象。虽曾有学者采用原状样进行试验，但受钻探进尺深度限制，以往试验样品多以浅表层试样为主[2]。当前国内外对厚层老黏土原状土研究较少，对其土动力特性研究还有待进一步开展。

国内外学者对交通荷载作用下土动力学特性研究也已取得一定成果。唐益群等[3]通过动三轴试验,研究地铁荷载作用下淤泥质土的临界动应力比及动应变随各因素的变化规律，同样对正常固结土临界动应力进行试验探究的还包括周 建等[4]。张勇等[5]采用循环动荷载不排水动三轴试验，分析得出饱和软黏土骨干曲线模型。陈颖平等[6]控制围压变化，拟合不同固结比作用下轴向应变及动强度与振次的关系。王常晶等[7]、温日琨等[8]则从初始静偏应力的角度研究其对饱和土动变形的影响。综合前人研究成果，土动力特性主要影响因素包括土动应力幅值大小(σd)、震动频率(f)、循环周数(N)、静偏应力(q)及固结比(Kc)等[9]。

高铁列车运行过程中产生的交通荷载，一般认为是长期疲劳循环荷载作用。交通荷载长期循环往复作用将可能使官厅地区的下伏厚层老黏土产生形变，从而对高铁运行安全造成严重影响。为研究京张高铁官厅段厚层老黏土在交通荷载作用下的动力学性质，利用GDS多功能三轴试验仪，考虑循环周次、动应力幅值大小、振动频率、固结应力等因素对老黏土土动力特性的影响，以期为未来高铁路基维护、沉降控制及类似工程问题提供参考依据。

1 厚层老黏土工程特性

通过钻探获取官厅地区内具有特殊结构的深层灰黑色湖相原状厚层老黏土(见图1b)。依据第四系地层资料及专家现场测定[10]，官厅地区厚层老黏土属上更新统马兰组中、下段(Q3m1+2)，局部为中更新统赤城组上段(Q2c2)。受官厅怀来盆地沉积物源及沉积历史等因素影响，厚层老黏土原为淤泥质土，经长时间固结作用，其物理力学性质发生改变。通过室内土工试验测得官厅盆地厚层老黏土的物理力学参数，并与全国内陆老黏土及上海地区浅埋淤泥质土物理性质指标进行对比(见表1)。

表1 不同地区天然状态下土的物理力学参数对比表[2-3,12]

将不同地区土的物理力学参数进行比对(见表1)，官厅地区厚层老黏土的平均天然密度可达2.072 g/cm3，略高于内陆及上海地区的淤泥质土，土体更为密实，故其孔隙比稍低于内陆及上海地区淤泥质土；测得厚层老黏土含水率约20.10%，较内陆及上海地区淤泥质土含水率低，土体更不易发生液化。对力学参数比对后可知，厚层老黏土的黏聚力约为80～211 kPa，远高于上海及内陆地区淤泥质土；测得内摩擦角结果约21.3°～38.4°，压缩模量约21.5～41.4 MPa，均高于上海及内陆地区淤泥质土；其压缩系数小于0.1 MPa-1，属低压缩性土，而上海及内陆地区淤泥质土为中—高压缩性土。

试验实测及对比分析结果表明，官厅地区厚层老黏土较全国内陆及上海浅埋淤泥质土埋深大，沉积历史较久，天然状态下土体密度较大，土体固结程度高，强度较高，具有弱膨胀性，失水后土体表面易崩解，未扰动时土的物理力学性状(见表1)接近于新近系顶部弱固结泥岩(见图1b)。故官厅地区厚层老黏土的工程性质良好。

以往研究结果表明[13]，淤泥或淤泥质土一旦扰动，土的结构受损可致使其强度迅速降低，甚至完全丧失。京张高铁桩基施工时，采用冲击成孔加旋挖施工方法(见图1a)，少数桩在成孔时对桩端老黏土的扰动强烈，扰动后土体状呈软塑状(见图1c)，说明成孔施工对土的强度损伤影响严重。在长期交通循环荷载作用影响下，厚层老黏土不断受扰动仍存在产生大幅形变的可能。

图1 官厅地区老黏土

2 动三轴试验

2.1 动三轴仪器及试验步骤

试验采用南京水利科学研究院岩土试验室GDS(Global Digital Systems)多功能三轴试验仪(见图2)，在GDS动三轴模块系统控制(DYNTTS)下进行。

图2 GDS多功能三轴仪

依据《土工试验规程》(SL237—1999)[14]，具体制样及试验方案按以下步骤进行：

(1)将原状土切削成高80 mm直径38 mm的试样，放置于水中，使用真空缸抽气至少24 h达饱和。

(2)将试验样品安装在三轴压力室内，试样上下均放置透水石，周围贴滤纸条加速排水，套橡胶膜。试样安装完成后安装压力室。

(3)向压力室内注水加压，对试样施加等向围压6 h，等压固结结束后轴向施加偏压q至预定值，进行偏压固结，固结时间与等压固结时间相同。

2.2 动三轴试验加载条件

选用偏压半正弦波近似模拟高铁列车动荷载，在固结不排水(CU)条件下进行试验[15-16]；侧压力系数则由John公式kc=1--sinφ′确定[17]，式中φ′为有效内摩擦角，其值选取时参考试验结果(见表1)近似取30°，计算侧压力系数kc=0.5。前人研究中定义循环周次1000次以上的交通荷载为长期疲劳荷载[13]。故本次试验终止条件设置为振动周次超过3000次或试样动应变大于5%，即停止试验。试验加荷过程如图3所示。

图3 GDS模拟循环动荷载波形图

试验时对不同试样主要控制加载围压、加载频率与动应力比等参数。为研究不同层位试样不同动应力比作用下老黏土的动力特性，暂不考虑桩的附加应力及阻尼效应，对不同围压及动应力比作用下的动荷载进行适当的放大，从而达到研究不同固结应力作用下极限状态土体动力特性的目的[18]。试验中对同一层位的试样选取控制不同动应力比进行试验，其计算公式为R=σd/2σ3。式中σd为动应力，σ3为侧向固结应力，单位均为kPa，动应力比用R表示。

高铁列车动频率参考经验公式f=V/L进行计算。式中f为动频率， Hz；V为列车车速，m/s；列车车厢长度L取固定值25 m[19]。本次试验设计对比2种不同动频率作用下土体动力特性。当列车速度为200 km/h时，列车频率约为2 Hz，列车速度为300 km/h时，列车频率近似取3 Hz。动三轴试验控制参数如表2所示。

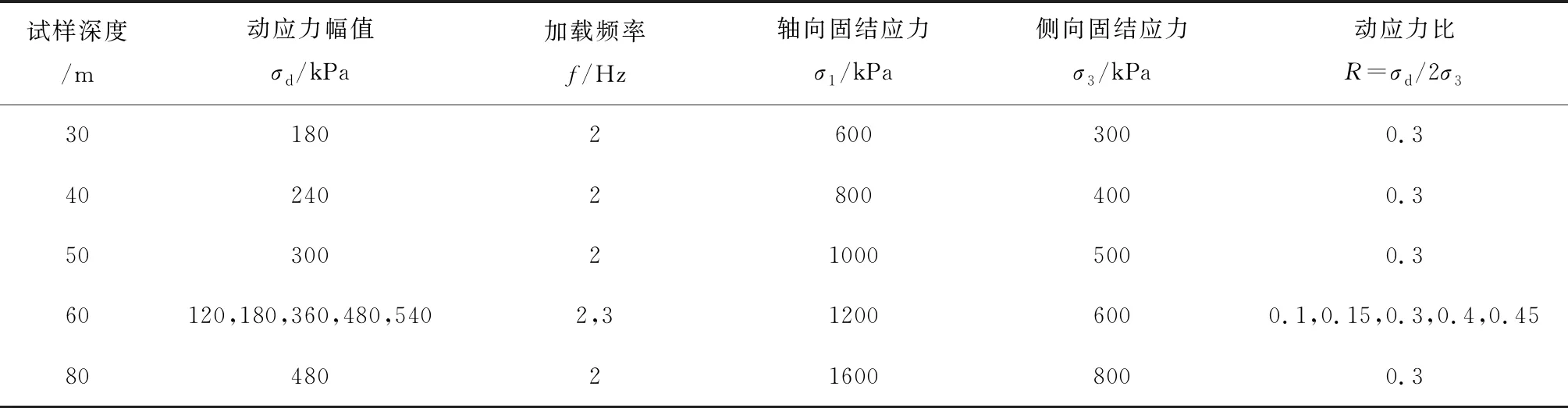
表2 动三轴试验控制参数汇总表

3 动三轴试验结果

依据厚层老黏土工程特性，对京张高铁官厅地区厚层老黏土原状样按照设计的试验步骤及不同的加载条件依次进行动三轴试验。通过对试验结果的整理，总结分析了在动应力比、动频率、固结应力等不同因素控制下循环周次与动应变之间的关系，并拟合了相应曲线的关系式。

3.1 结果分析

3.1.1 动应力比对动应变的影响

以深60 m的官厅地区厚层老黏土原状样为对比研究对象，当控制频率及固结应力一定时，不同动应力比加载条件下土体动应变随振动周数变化如图4所示。

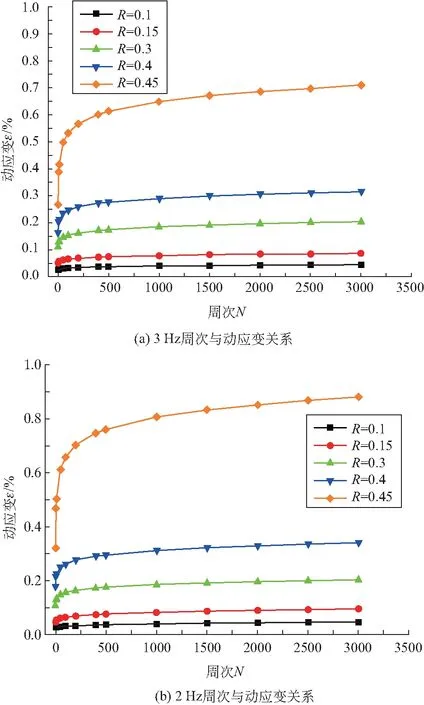
图4 振动次数与动应变关系图(60 m)

由试验结果可知，同一深度不同动应力幅值作用下，60 m厚层老黏土振次达3000次后，试样轴向动应变均未达5%。当土样埋深及动荷载振动频率一定时，老黏土动应变随循环周次的累加呈增长趋势；在前100次振动过程中，土体动应变随振次的增加迅速发展；随着振次不断增加，试样产生的轴向动应变速率逐渐趋于平缓。是在长期动荷载作用下，土体颗粒之间受振压密所至。随着土体不断被压密，孔隙水压力逐渐增大，土样内产生反压使其难以进一步发生形变，应变量逐渐趋于稳定。学者们普遍定义在动应力作用下，土样未发生明显剪切破坏，动应变逐渐趋于稳定的曲线为稳定型[2]。

由图4(b)可见，对于2 Hz的试样，当R=0.1时，土体产生的最终动应变约为0.047%；当R=0.15时，土体最终动应变约为0.095%，为R=0.1时最终动应变幅值的2倍；当R=0.45时，土体最终动应变达到0.889%，较R=0.1时增加近18倍。土样动应变幅值随动应力比的增大发展迅速，即较大的动荷载对土体动应变发展作用更明显。

3.1.2 动频率对动应变的影响

依据试验结果(见图4)将各动应力比作用下的不同动频率产生的最终应变进行比较(见图5)，可知在同一深度同一应力比荷载作用下的样品，低频产生的动应变较高频产生的动应变更显著。产生这种现象是由于土体受动荷载作用产生变形需要一定时间，而振动频率越快，留给土体变形反应的时间越短。土颗粒间受高频振动作用还未来得及变形完全就已进入下一周次振动，故高频作用下土体受动荷载作用反应时间不如低频荷载时间长，造成高频土样土体变形量便不如低频荷载明显。由图5还反映出在不同频率作用下，动应变之差随动应力比的增长呈增大趋势。试验结果基本符合这一基本规律，但由于受人为扰动等多因素影响，部分数据具有离散性。试验也仍存在加载频率相对较少，难以详细刻画多个频率作用下动应变随频率变化曲线的问题。

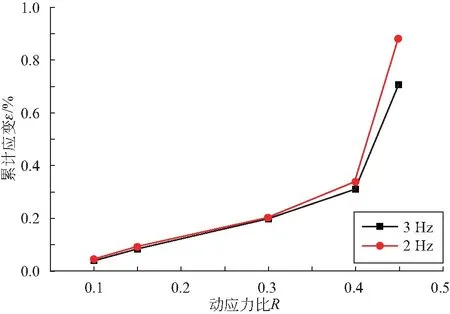
图5 频率控制动应力比与最终动应变关系图(60 m)

3.1.3 固结应力对动应变的影响

当控制动应力比(R=0.3)及动频率(2 Hz)一定时，不同深度固结应力作用下土体振次与动应变关系如图6所示。根据试验结果得到不同振次不同深度土体动应变随与周次发展情况如表3所示。

图6 围压控制振动次数与动应变关系图(2 Hz,R=0.3)

由图6(a)可见，在相同的频率及动应力比加载条件下，不同深度土体应变的发展幅度及速率明显不同。30 m的土样振动至430次左右时，动应变已经大于5%，即样品已破坏；40 m及 50 m的土样振动3000次后，产生最终动应变接近于4.5%，虽未达5%的破坏值，但样品动应变已接近试验中止条件；振次至430次左右时，各个试样动应变均已超过最终应变量70%以上，但很快动应变曲线便趋于稳定，周次与动应变的半对数曲线斜率也逐渐趋于平缓；60 m与80 m的样品曲线最终动应变未超过1%，振动周数至430次时，变形量已超过最终变形量的80%，随后变形量逐渐趋于一常数。

根据图6(a)试验曲线可绘制同应力比同动频率作用下不同深度试样周次--动应变速率曲线。由动应变发展速率曲线(见图7)及动应变比随振次变化表(见表3)可知，土样动应变发展速率随深度不同有所差异，且振动动应变发展速率与土体最终应变量大小有关。30 m土样初始动应变增长较40 m与50 m的试样慢，但其周次与动应变发展曲线近似呈直线，属破坏型曲线。40 m与50 m的土样性质相似，40 m试样初试发展速率与50 m的土样相比，其动应变增长速率较慢。但50 m试样动应变达稳定的振次少于40 m的试样，其最终动应变均接近4.5%，故40 m与50 m样品在当前动荷载作用下处于临界状态。60 m与80 m的样品性质类似，几乎刚受动荷载作用土体就进入稳定状态，土体强度较大，产生的最终变形量不大，振次与动应变关系属稳定型。

图7 不同深度周次-动应变速率曲线图

表3 不同深度土体动应变发展随周次变化表(500次内)

以上规律说明土样固结应力对试样动变形及变形速率均有一定影响。土体所受固结压力越大，在相同动应力比及相同频率的加载条件下，土体产生的动应变越小，动强度越大。土体应变量与固结压力大小呈负相关。但前期振动阶段，土体应变增长速率却与土体围压的大小呈正相关，且固结压力越大的土体进入稳定阶段所需的振动周次越少。官厅地区厚层老黏土呈现该现象的原因与土体自身固结历史有一定的关系。

3.2 公式拟合

从京张高铁埋深60 m不同应力比的土体试验结果不难发现(见图4)，土体动应变均未超过1%，属于稳定型发展曲线。符合Monismith C L等提出的ε=aNb稳定型曲线指数模型[20]。为了更好反映规律，采用振次与动应变的半对数曲线(lgN-ε)表示其发展关系(见图8)。由图可知振次与动应变的半对数曲线可近似用一直线方程表示，且斜率随动应力比的增大呈不断增长趋势。故y=A+BlgN线性模型能够更简单地拟合周次与动应变的关系。式中N表示循环周次，A为直线截距，表示第一次振动土体产生的塑性变形量；B为直线斜率，代表的是循环加载作用过程中土体动应变的发展速率，该参数与土体的动强度相关。采用origin软件对60 m试样(见图8)周次--动应变半对数曲线进行拟合，得到拟合参数如表4所示。计算得相关系数r2值较高，满足数据离散性要求。由拟合结果可知，相同固结应力同一频率动荷载作用下，土样周次--动应变半对数曲线表示动应变发展速率的B值随动应变比的增大呈增长趋势；且相同动应力比条件下，2 Hz土体动应变的发展速率较3 Hz的快。

图8 振动次数与动应变半对数关系图(60 m)

表4 同一深度不同频率不同应力比拟合半对数曲线参数表(60 m)

借助origin软件，对动应力比R=0.3时不同深度动荷载作用下的土体的动应变-周次半对数曲线关系进行拟合。由图6(b)可知对于30 m的土样，动应变-周次的发展曲线呈破坏型，拟合破坏型曲线方程y=a·elgN/t1+y0，其中N为振次，a、y0、t1、t2为拟合参数，r2为相关系数；40 m至50 m的土样曲线近临界型，拟合临界型曲线方程y=y0+a(1-elgN/t1)+b(1-elgN/t2)，其中N为振次，a、b、y0、t1、t2为拟合参数，r2为相关系数；60 m以下的土样，动应变-周次发展曲线为稳定型。稳定型曲线方程近似拟合为线型y=a+blgN，其中a、b为参数，N为振次。具体拟合参数及相关系数如表5所示。

表5 不同深度振次动应变半对数曲线拟合参数表

4 结论

(1)京张高铁厚层老黏土在天然状态下物理力学性质较一般浅埋淤泥质黏土好，土体密实度较大，含水率及孔隙比均低于一般淤泥质土。这与老黏土自身受到的固结应力与固结历史有关。

(2)京张高铁不同深度厚层老黏土的动力特性不同，在相同动应力比相同频率作用下，固结压力小的土体变形更明显。振动初期，固结压力大的土体应变发展速率快，达到稳定发展阶段所需振次越少。在动频率2 Hz、动应力比为0.3的相同加载条件下，30 m的土体产生变形量较大，40～50 m的土样处于临界状态，60 m以下土体较稳定。故京张高铁应对30～50 m桩端土变形量加以监测。

(3)埋深为同一深度的土体在不同动应力比作用下，土体应变量随加载动应力的增加而增大。在不同频率的动荷载作用下，同一深度的土体动应变于低频率作用下发展更为显著。

(4)由origin软件拟合不同深度及不同固结应力比作用下振次与动应变关系数学表达式，拟合结果可为京张高铁后期沉降控制提供参考依据。

当前，交通荷载作用下高铁造成不均匀沉降问题为限制城市间交通运输速度的障碍之一。我国对老黏土原状土动力特性研究较欠缺，未来仍有待进一步开展土体的动力学特性、土本构模型关系、交通荷载长期沉降量的预测等方面的研究。