基于栅格化四边形区域与改进人工势场的车辆行驶轨迹研究
任少杰,杨正才,张英泽
(1.湖北汽车工业学院 汽车工程学院,湖北 十堰442002;2.上海汽车集团股份有限公司 前瞻技术研究部,上海201804)
近年来,各大企业与高校加大了无人驾驶方向的研究力度,其中无人驾驶技术的关键在于确保车辆行驶安全。在未知且复杂的行车环境中,为了减少与障碍物碰撞而引发交通事故的可能性,无人驾驶汽车的路径规划研究就显得十分重要。Khatib[1]在1986 年首次提出了人工势场法,并应用于机器人避障的路径规划。该方法计算量小,实时性好,便于底层控制,但存在局部极小值和震荡的缺陷。Huang Z[2]等为了实现复杂环境下的协同驾驶,提出了一种基于人工势场法和模型预测的组合控制方法。李明[3]将汽车的转弯半径引入人工势场法,并利用该方法对智能车进行路径规划,保证了汽车在避障过程中能够保持一定的稳定性与舒适性。刘洲洲[4]基于改进人工势场法进行无人车的路径规划,通过设置角度偏移量改变斥力方向,避免陷入局部极小值的问题。杜[5]等在传统人工势场法中添加了速度参数,通过改变势场函数和初始条件解决了局部最优、碰撞和目标点不可达的缺陷。吴乙万[6]等在传统人工势场法的基础上加入了动态虚拟障碍物的概念,根据车辆的行驶状态,行驶环境以及交通法规来评估车辆行驶的安全性,获得虚拟车道线的数学表达式,然后生成车辆行驶决策与动态虚拟障碍物,最后利用改进人工势场法进行局部路径规划。
文中提出一种基于栅格化的四边形区域建模方法,并利用改进的人工势场法进行路径规划,可以有效克服障碍物在目标点附近时的目标不可达的缺陷,避免陷入局部最优的问题。
1 基于四边形的区域建模
以笛卡尔坐标系的第一象限作为环境地图,将某四边形区域分为空区域、障碍内区域和目标内区域,如图1 所示。图中c1、c2、c3为车辆,s1为空区域中的小型障碍物,2个正方形阴影区域为障碍内区域。设G ∈R2为由四边形化算法生成的一组不规则的四边形区域组成的工作空间。四边形区域表示如下:



图1 四边形区域的划分

通过利用四边形进行区域建模得到G 中各区域的顶点和各个区域的拓扑结构。文中进行以下假设:1)假设已知每个障碍物中心的位置,即(xm,ym),m为障碍物数量;2)假设已知G中连接起始点和目标点的区域序列。

2 改进人工势场法模型
人工势场法易用数学公式表达,计算量较小,广泛应用于路径规划领域。传统人工势场法存在局部最优,导致无人驾驶车辆出现抖动、目标不可达、规划路径与障碍物距离过近等缺陷,因此在障碍物势场函数中加入路径点与目标点相对距离参数,改进人工势场法。
2.1 目标引力势场能模型
无人车与目标点之间的距离影响无人车的引力势场能,两者之间的距离越大,无人车所受到的引力势场能值越大,反之无人车所受到的引力势场能值则越小。引力势场函数为

式中:Yatax(i)为目标点对无人车的引力在x 轴方向上的分力;Yatay(i)为目标点对无人车的引力在y轴方向上的分力;m为引力影响因子;rat为路径点与目标点之间的距离;α为目标点与路径点的连线和路径的夹角。
2.2 障碍物斥力势场能模型
障碍物与无人车路径点的距离影响障碍物斥力。当无人车在障碍物影响范围之外时,斥力为零;当无人车在障碍物影响范围之内时,两者之间的距离越大,无人车受到的斥力越小,其斥力势场能就越小。当障碍物与目标点距离过近时,障碍物斥力势场加入路径点与目标点距离因素,可减少障碍物斥力势场能,从而使目标点为全局最小值,克服目标不可达问题。斥力势场函数为
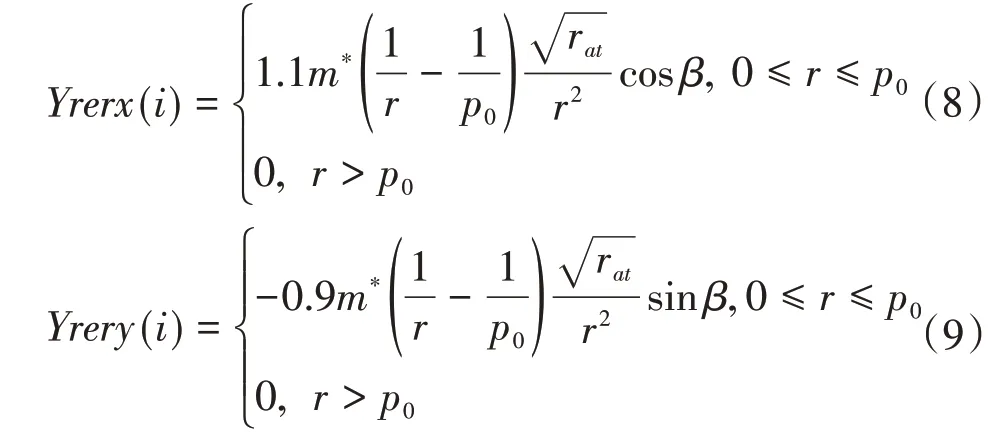
式中:Yrerx(i)为障碍物对无人车的斥力在x轴方向上的分力,Yrery(i)为障碍物对无人车的斥力在y轴方向上的分力,正负号代表斥力对无人车的方向,设定在每个坐标轴上方向与车辆行驶方向一致的力为正,反之为负;m*为斥力影响因子;r为无人车的路径点与各障碍物间的距离;p0为障碍物的影响范围;β为障碍物和路径点连线与路径的夹角。
2.3 合力势场能模型
无人车受到目标点引力势场和障碍物斥力势场组成的复合场作用力,行驶至目标点的过程中会同时受到多个障碍物的斥力势场力。图2 是车辆受力示意图,Frer1和Frer2是障碍物对无人车的斥力,Fat 是目标点对无人车的引力,F 是两者合力。由式(5)~(8)可知,无人车受到的势场力值由多个障碍物对无人车的斥力和目标点对无人车的引力组成。x 轴方向与y 轴方向的合力势场函数如式(10)~(11)所示:

图2 无人车受力示意图

3 栅格地图与改进人工势场法
栅格地图将某地图划分为数量有限、大小相等的方格,用不同代码表示某一方格是否有障碍物,最终搜索出能有效避开障碍物到达目标点的路径。
3.1 子目标点的选择

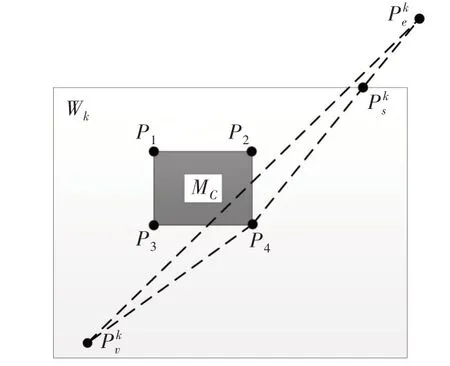
图3 子目标点的选择
3.2 势场值的更新计算
使用梯度下降法生成连接起点和终点的路径。由于目标区域被定义为最低势场,每个栅格点有且仅有1个梯度方向,因此可以找出从任意点到目标区域的路径。根据狄利克雷边界条件,每个栅格点的势场值计算公式为
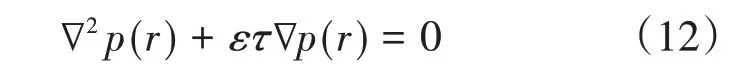
式中:τ为偏差单位向量;ε为系数。调节2个参数可以提高搜索效率。当ε为0 时,式(12)计算量最小且其路径规划时间最短,此时生成的路径为最优路径,但是在复杂环境中很难实现。为了避免这个缺陷,初始化狄利克雷边界条件,即设置水平窗口障碍物的边界条件为1(最高势场),目标区域为0(最低势场),其他方格的势场值根据式(13)更新,如图4所示。
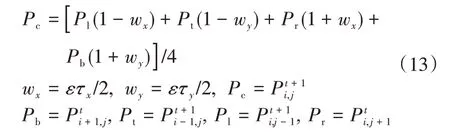
式中:Pc为中心栅格的势场值;Pb为底部栅格的势场值;Pt为顶部栅格的势场值;Pl为左部栅格的势场值;Pr为右部栅格的势场值;i 和j 为栅格坐标;t为当前时刻,( t + 1 )为下一时刻。当wx∈[-1,1]且wy∈[-1,1]时,根据式(13)可得

式中:Pmin为势场最小值,代表目标区域势场值;Pmax为势场最大值,代表障碍物和边界的势场值。设置ε ∈[-2,2],使势场值满足边界条件,保证每个栅格梯度下降方向指向目标区域,同时获得避开障碍物和边界的趋势,使无人车顺利到达目标点。

图4 势场计算栅格分布图
3.3 势场梯度下降方向的确定
根据势场值公式计算每个栅格的梯度:

行驶方向的选择如图5所示,假设当前时刻无人车的位置为H(i,j),行驶方向为∇Pi,j,设置H(i,j)为中心点,平均分割中心点周围的8 个栅格,找到梯度指向的区域。图5 中下一个预期行驶方向为∇Pi-1,j+1,中 心 点 为H(i - 1,j + 1)。如 果∇Pi,j和∇Pi-1,j+1的方向相距较远,无人车不会按照式(14)生成的路径行驶,而是调整行驶方向为

式中:φcurrent为当前时刻无人车的行驶方向;φnext为无人车预期行驶方向;φnew为无人车实际的行驶方向;η ∈[0,1)为系数。在这种情况下,无人车根据φnext行驶,直到梯度方向可以直接作为行驶方向,拟合生成路径并将其作为无人车实际行驶路径。

图5 行驶方向的选择
4 仿真分析
栅格化后的四边形区域如图6 所示,图中2 个方块为障碍物区域,4个十字标记围成1个小栅格,小栅格的边长为1 m,形成分辨率为1栅格化地图。设置无人车起始位置为(2,1),障碍物影响距离为2.5 m,障碍物个数为15,引力影响因子为50,步长为10,斥力影响因子为10,迭代次数为200,无人车的目标位置为(10,10)。基于Matlab仿真生成的路径子目标点如图6所示。

图6 改进人工势场+栅格法路径规划结果
为了使生成的路径能够避免车辆与障碍物发生碰撞,采用五次多项式拟合子目标点,拟合效果如图6所示。虽然可顺利到达目标点,但是拟合的路径存在曲线部分不光滑的现象,车辆的行驶轨迹一般是光滑曲线,所以五次多项式拟合在一定情况下不符合行驶要求。采用贝塞尔(Bezier)曲线拟合可解决这一问题,如图6所示。通过比较2个拟合结果发现,贝塞尔曲线的拟合效果更好,曲线更加光滑,可保证车辆正常行驶。
5 实验结果与分析
实验用小型无人车通用线控化底盘长1.65 m、宽0.9 m、高0.4 m,车上装有1个十六线激光雷达和1个双目摄像头,利用十六线激光雷达对周围的环境进行感知探测障碍物,为实现车辆避障提供环境感知条件,如图7所示。
实验环境如图8 所示,在车辆前方设置2 个纸箱障碍物和1 位行人,以车辆起始点为坐标原点,目标终点设置为(2.3,7.7),左右侧纸箱障碍物坐标为(-0.9,4.3)和(1.5,3.5),行人坐标为(-1.1,3.3)。

图7 实验用车

图8 实验环境

图9 改进人工势场法与改进人工势场+栅格法路径轨迹
图9a~9b 中引力势场值随着斥力势场值的增大而增大,原因是为了使小车达到终点,需要克服障碍物的斥力势场值,当小车远离障碍物时,引力势场值有恢复到正常值的范围。根据图9c可以看出,加入栅格法后,优化了小车的行驶路径,与左右侧障碍物距离适中,从而保证行驶过程更加安全。
6 结论
1)解决了传统人工势场方法中障碍物与目标点过近,而存在目标不可达的缺陷,目标点成为势场最小值,从而可以使局部最优和目标不可达的问题得到有效解决。
2)将栅格化与改进人工势场法结合进行路径规划,并改进无人车向斜方向进行移动,使无人驾驶车辆能够较安全的避开障碍物顺利到达目标点。
3)避免陷入局部最优的问题,通过栅格化地图,根据无人驾驶车辆到目标点的最近距离为判断条件进行移动,即可以有效解决局部最优,且规划出的路径最短。

