“居高临下”方能“深入浅出”——具有高等数学背景的试题的背景分析及解法探微

姜卫东

(江苏省扬州中学 225009)

随着高中数学里高等数学的含量进一步扩大，近几年在高考及模拟试卷中，经常会出现以高等数学为背景的试题，这些试题背景丰富、立意高远，既考查学生当下的数学素养，又考查学生将来的学习潜能.在解决它们时，由于学生知识与方法的限制，只能遵循“高等背景，初等解法”的原则.接下来，笔者就几种有高等数学背景的试题进行背景分析，并探究其初等解法.

一、高数的背景类型

1.以泰勒公式为背景

例1设函数f(x)=x(ex-1)-ax2,若当x≥0时，都有f(x)≥0,求实数a的取值范围.

初等解法：由于f(x)=x(ex-1-ax),又x≥0，故只需证明ex-1-ax≥0,设g(x)=ex-1-ax.g′(x)=ex-a.考虑到ex≥1,为确定g′(x)的正负，应分a≤1与a>1进行讨论.(1)若a≤1,则当x∈(0,+∞)时，g′(x)>0,g(x)为增函数.而g(0)=0,从而当x≥0时，g(x)≥0,即f(x)≥0.(2)若a>1,则当x∈(0,lna)时，g′(x)<0,g(x)为减函数.而g(0)=0,从而当x∈(0,lna)时，g(x)<0,即f(x)<0.综合得a的取值范围为(-∞,1].

解法感悟：对于与泰勒公式有关的题型，解题的关键在于构造函数(而这个函数是由背景分析的逆推而来)，利用导数研究函数的相关性质，再根据函数的性质进行解不等式或不等式证明.在上面解题过程中，当a>1时，对于这种不符合题意的情形，只要找到一个区间，然后证明在此区间上不成立即可.

2.以拉格朗日中值定理为背景

例2已知函数f(x)=(a+1)lnx+ax2+1.

(1)讨论函数f(x)的单调性；(2)设a<-1,如果对任意x1,x2∈(0,+∞),都有|f(x1)-f(x2)|≥4|x1-x2|,求a的取值范围.

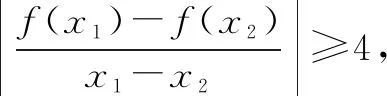
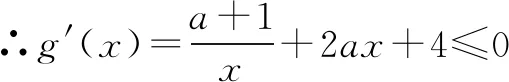
解法感悟：对于与拉格朗日中值定理有关的题型，关键在于对不等式进行等价变形，根据式子的结构特征，构造同构函数，利用函数的单调性进行解题.

3.以伸压变换为背景

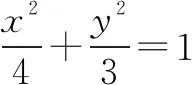
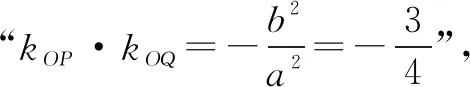
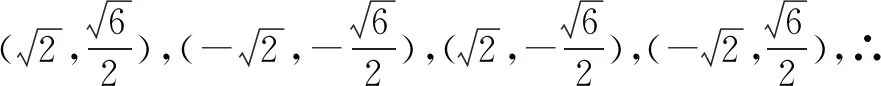
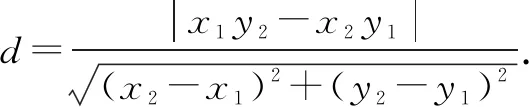
解法感悟：对于与伸压变换结合的题型，应先通过特定的位置(或情形)得到可能的定值，然后通过设点或设线的方法进行论证或求解.

4.以极点极线为背景

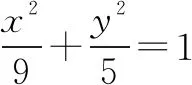
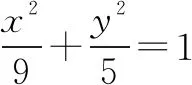
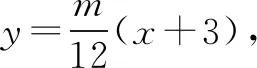
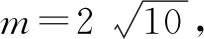
解法感悟：对于与极点极线有关的题型，常见的处理方法有两种：一是先特殊后一般的思想方法，可以根据图形的对称性或特殊位置先得到结论，再验证在一般情形下结论也成立；二是建立与极点有关的方程，通过方程来研究极点的相关性质.

5.以定积分公式为背景(微积分基本定理)

例5设函数f(x)=ln(1+x),g(x)=xf′(x),x≥0，其中f′(x)是f(x)的导函数.

(1)g1(x)=g(x),gn+1(x)=g(gn(x)),n∈N+，求gn(x)的表达式；

(2)若f(x)≥ag(x)恒成立，求实数a的取值范围；

(3)设n∈N+，比较g(1)+g(2)+…+g(n)与n-f(n)的大小，并加以证明.

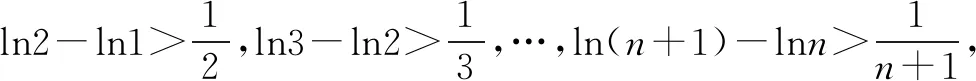
解法感悟：对于与定积分有关的题型，可以通过构造不等式，然后进行赋值累加即可；也可以先归纳猜测结论，再利用数学归纳法进行证明.

6.以不动点为背景

解法感悟：对于与不动点有关的题型.关键是利用递推关系进行迭代，将题设中的不等关系等价转化为初始元素的不等条件.

7.以数列极限为背景

例7是否存在各项都是正整数的无穷数列{cn},使得cn+12>2cncn+2对一切n∈N*都成立?若存在，请写出{cn}的一个通项公式；若不存在，请说明理由.

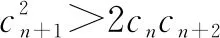
解法感悟：解决与数列极限有关的题型.关键在于深刻理解数列极限的定义，借助已知条件，构造合适的N,使得从数列中某一确定的项(如aN)以后的所有项都符合题设.

二、我们的策略

1.“居高临下”的意识

现行的新课改要求教师应该具有较高的高数素养，只有这样才能深刻理解中学数学问题的来龙去脉，才能用“高观点”来审视中学问题.因此，中学教师应熟练掌握中学教材中所蕴含的高数思想，厘清高等数学与初等数学试题的结合点，并注重研究、剖析以高数为背景的各类试题，准确把握高考命题的走向.

2.“深入浅出”的能力

尽管出现了以高数为背景的试题，但这些高数知识仅仅是为了创设一种情境，并不要求学生要用高数知识来解决.作为中学教师，应该将重心放在中学数学的基本知识和基本思想方法上，通过中学生熟悉的“通性通法”来解决这类题型，这才是教学研究的根本之所在！