双圆破解直线边界磁场的临界及几率问题

王隆洋

(浙江省宁波外国语学校，浙江 宁波 315121)

1 模型母题

(1) 荧光屏发光区域的长度L1以及能打在荧光屏发光区域的粒子占总粒子数的比例η1.

(2) 两次发光的区域长度L2以及能打在二次发光区域的粒子占总粒数的比例η2.

图1

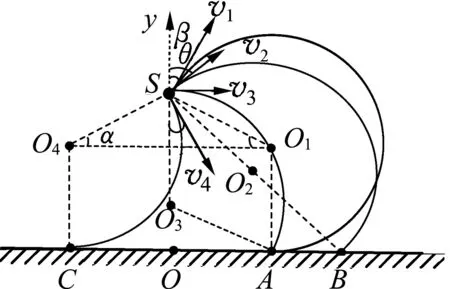
图2

2 分析

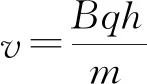
综上所述，若粒子做顺时针圆周运动，4个特殊轨迹圆就是O点左右各一个相切圆，右侧两个相交圆.圆O2是直径相交圆，圆O1与圆O4关于y轴对称，且α=β，圆O1与圆O3为共弦长的互补圆，四边形O1SO3A是菱形.同理可知若粒子运动方向为逆时针圆周运动，则两个相交圆在O点左侧.

3 模型构建

双圆限区域，一交一切定边界，出射速度定几率.示意图如图3所示.

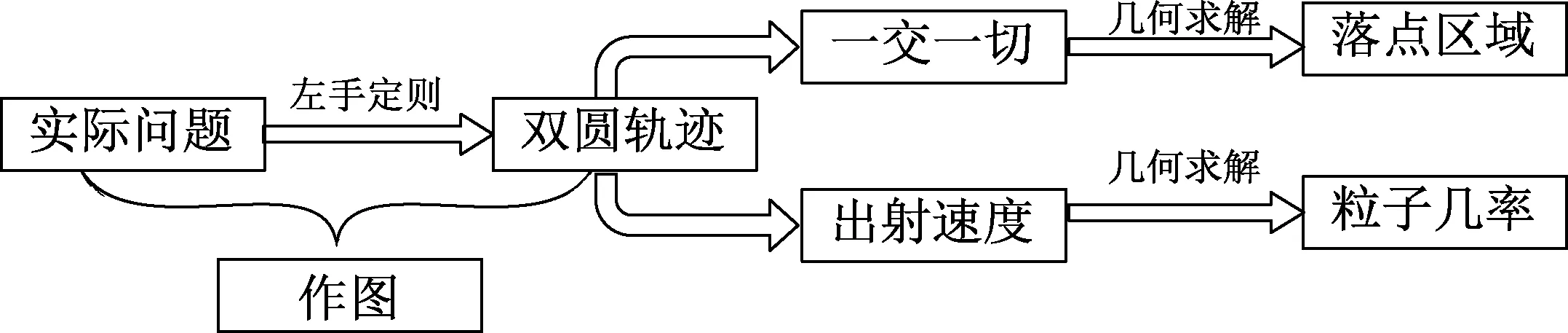
图3

4 实际问题求解

(1) 求发光区域长度L1.如图2所示，双圆为圆O2和圆O4，一交一切即为圆O2直径与荧光屏的交点B和圆O4与荧光屏的切点C，由几何关系求得

(3) 求两次发光的区域长度L2.双圆为圆O1和圆O3，一交一切即为圆O1与荧光屏的切点A和圆O3直径与荧光屏的交点B，由几何关系求得

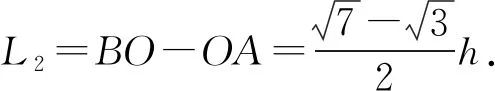
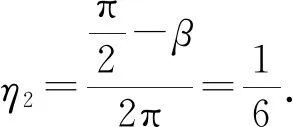
图4

实际问题拓展示例：荧光屏O点右侧为有限宽，如图4所示，若轨迹圆O2的直径在OA的延长线上，则荧光屏发光区域右端最远点就是荧光屏的右端点A.

总之，模型来自于实际问题，但运用模型解决实际问题时要质疑创新、具体问题具体分析.

5 例题分析

图5

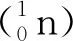
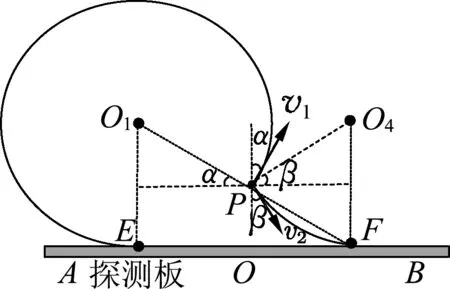
图6

已知电子质量me=9.1×10-31kg=0.51 MeV/c2，中子质量mn=939.57 MeV/c2，质子质量mp=938.27 MeV/c2(c为光速，不考虑粒子之间的相互作用).

若质子的动量p=4.8×10-21kg·m·s-1=3×10-8MeV·s·m-1，

(1) 写出中子衰变的核反应式，求电子和反中微子的总动能(以MeV为能量单位).

(2) 当a=0.15 m，B=0.1 T时，求计数率.

(3) 若a取不同的值，可通过调节B的大小获得与(2)问中同样的计数率，求B与a的关系并给出B的取值范围.

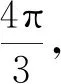
图7

6 总结

这道压轴题强化了对学生核心素养的评价，要求学生能将较复杂实际问题的对象和过程转换成物理模型，能对综合性物理问题进行分析和推理，运用物理观念解决实际问题.[3]本文通过分析4个轨迹圆的特征及内在联系，将实际问题转化为具体的双圆数学模型，化解了这类直线边界磁场的临界及几率问题难度.