分形集上Lipschitz 函数的Hermite⁃Hadamard⁃Fejér 型不等式

时统业

（海军指挥学院， 江苏 南京211800）

0 引言

对于［a，b］上的凸函数f，成立下面的Hermite⁃Hadamard 不等式

文［2］对于满足M－Lipschitz 条件的函数给出由式（1）生成的差值的估计.

定理1［2］设函数f在［a，b］上满足M－Lipschitz 条件，即存在常数M，使得对于任意x、y∈［a，b］，有｜f（x）－f（y）｜≤M｜x－y｜，g是［a，b］上的正的可积函数且关于（a＋b）／2 对称，则有

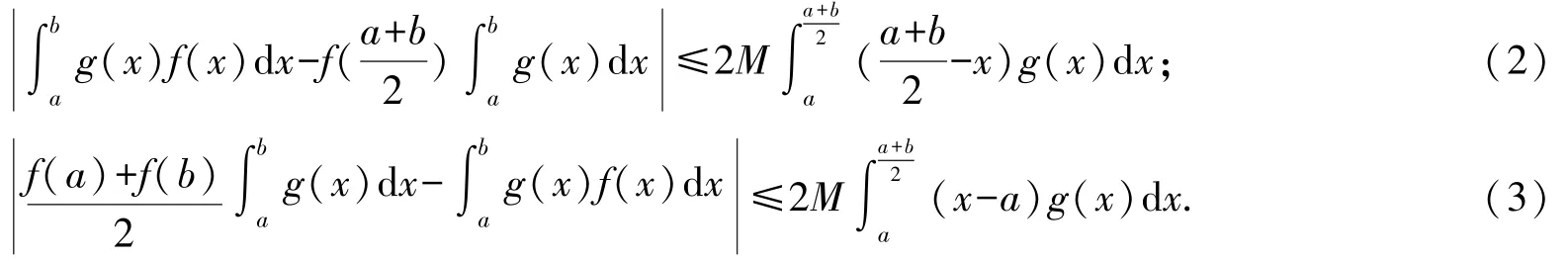
文［3］对于（m，M）－Lipschitz 函数给出式（2）的推广.

定理2［3］设f是［a，b］上的（m，M）－Lipschitz 函数，g是［a，b］上的正的可积函数且关于（a＋b）／2 对称，则有

杨小军在文［4］中系统阐述了建立在分形空间上的局部分数阶微积分的相关理论.局部分数阶导数和局部分数阶积分的定义可参见文［4］，这里不再赘述. f∈Cα（I）表示f在区间I⊆R 上局部分数阶连续. f∈Dα（I）表示f在区间I⊆R 上局部分数阶可导. f的局部分数阶导数记为表示f在区间［a，b］⊆R上的α阶局部分数阶积分.

引理3［5］（局部分数阶积分的换元法） 设f（x）在［a，b］上连续，函数x＝g（t）满足条件：

引理4［6］（局部分数阶微分中值定理） 设函数F（x）在［a，b］上连续，在（a，b）上α阶局部分数阶可微，则对于任意x0、x∈［a，b］，x0＜x，存在ξ∈［x0，x］，使得

引理5［5］（局部分数阶定积分上限的函数的导数） 设f∈Cα［a，b］，0＜α≤1，积分上限函数定义为

定义1［7］设区间I⊆R，函数f：I→Rα，若对任意u、v∈I和任意λ∈［0，1］，有

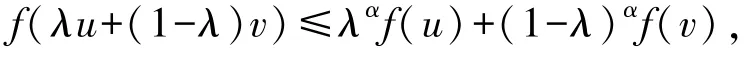
则称f是I上的广义凸函数.

定理3［7］（广义凸函数的Hermite⁃Hadamard 型不等式） 设上的广义凸函数，则有

定理4［8］（广义凸函数的Hermite⁃Hadamard⁃Fejér 型不等式） 设上的广义凸函数，g：［a，b］→Rα是非负的局部分数阶可积函数且关于

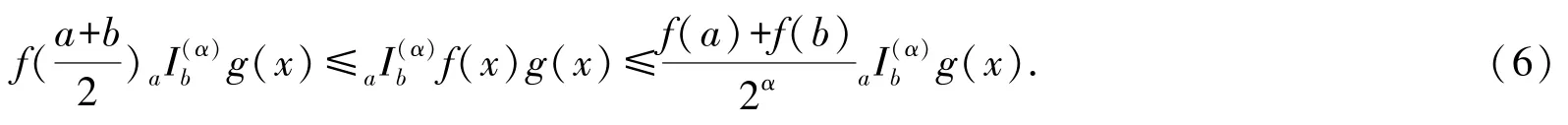
本文目的是在（m，M）－Lipschitz 条件下给出由式（6）生成差值的估计.为方便起见，记

1 主要结果

定理5设f∈Cα［a，b］，f是［a，b］上的α阶（m，M）－Lipschitz 函数，g：［a，b］→Rα是［a，b］上非负的局部分数阶可积函数且关于（a＋b）／2 对称，则有

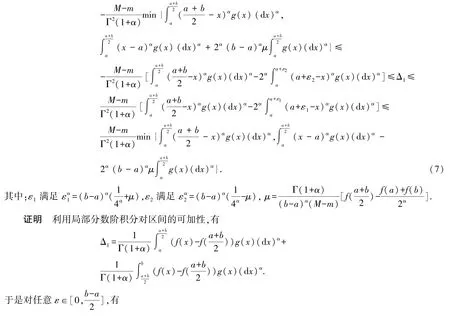
其中利用了下面事实：

利用引理5 得

由已知条件有

综合式（12）～（14）和式（17），则式（7）右边两个不等式得证.当f在［a，b］上满足α阶（m，M）－Lipschitz 条件时，－f在［a，b］上满足α阶（－M，－m）－Lipschitz 条件.对函数－f应用已证结论，则式（7）的左边两个不等式得证.

推论1设f在［a，b］上满足（m，M）－Lipschitz 条件，g是［a，b］上非负的可积函数且关于（a＋b）／2 对称，则有

证明在定理5 中取α＝1 即可得证.

推论2设f∈Cα［a，b］，f在［a，b］上满足α阶（m，M）－Lipschitz 条件，g：［a，b］→Rα是［a，b］上非负的局部分数阶可积函数且关于（a＋b）／2 对称，则有

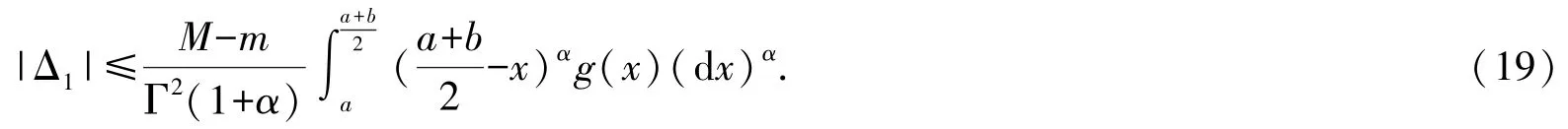
注1式（19）是式（4）在分形集的推广.

推论3设f∈Cα［a，b］，f在［a，b］上满足α阶（m，M）－Lipschitz 条件，则有

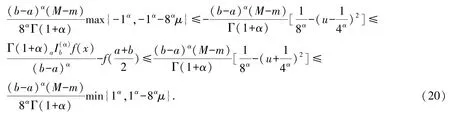
证明在定理5 中取g（x）≡1，并利用引理2，则推论3 得证.

推论4设f∈Cα［a，b］，f在［a，b］上满足α阶（m，M）－Lipschitz 条件，则有

定理6设f∈Cα［a，b］，f是［a，b］上的α阶（m，M）－Lipschitz 函数，g：［a，b］→Rα是［a，b］上非负的局部分数阶可积函数且关于（a＋b）／2 对称，则有

因为f是［a，b］上的α阶（m，M）－Lipschitz 函数，所以有

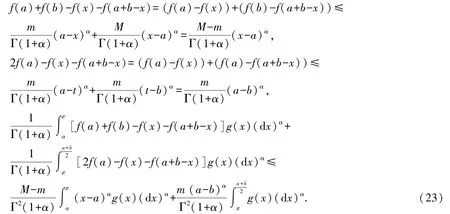
综合式（22）～（23）得Δ2≤φ2（ε）.其中：

于是有

综合式（24）～（27）得

综合式（28）～（29），则式（21）成立.

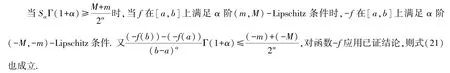
注2式（21）给出式（5）在分形集中的推广.

推论5设f在［a，b］上的（m，M）－Lipschitz 函数，g是［a，b］上非负的可积函数且关于（a＋b）／2 对称，则有

证明在定理6 中取α＝1 即可得证.

推论6设f∈Cα［a，b］，f是［a，b］上的α阶（m，M）－Lipschitz 函数，则有

证明在定理6 中取g（x）≡1，并利用引理2，则推论得证.