基于Boruta和极端随机树方法的森林蓄积量估测

韩 瑞,吴达胜,方陆明,黄宇玲,4

(1.浙江农林大学 信息工程学院,杭州 311300；2.林业感知技术与智能装备国家林业和草原局重点实验室,杭州 311300；3.浙江省林业智能监测与信息技术研究重点实验室,杭州 311300；4.醴陵市陶瓷烟花职业技术学校,湖南 醴陵 412200)

森林蓄积量(Forest Stock Volume,FSV)是指一定面积上的林木树干部分的总材积,反映了一个国家或地区森林资源总体规模的大小,是全国森林资源调查的一项重要内容[1]。森林蓄积量体现了森林生态系统林分信息,与森林生物量、生物多样性和碳储量等息息相关,是反映森林资源数量的重要指标,已经成为林业科学研究中的重点内容[2]。基于森林大数据的蓄积量估测,通过特征选择可以降低原特征集的维度以及减少冗余信息,达到提高预测精度以及减低模型训练耗时的目的[3]。刘明艳等[4]采用主成分分析方法对实验数据进行降维,利用线性回归方法建立森林蓄积量估测模型,并取得良好的效果；周如意[5]选用相关性分析对所有自变量因子进行筛选,通过多元线性回归、偏最小二乘法以及广义回归神经网络分别建立森林蓄积量估测模型,对龙泉市森林蓄积量进行全局预测；王海宾等[6]基于高分一号遥感影像数据,使用K-最邻近方法(K-Nearest Neighbor,KNN)建立延庆区森林蓄积量估测模型,并与偏最小二乘回归方法进行对比,结果显示KNN方法优于偏最小二乘回归方法；Wu[7]通过Levenberg-Marquardt(LM)优化算法(LM-BP)改进反向传播(BP)神经网络(NN)模型估测龙泉市森林资源蓄积量；汪康宁等[8]以黑龙江凉水自然保护区为研究对象,使用随机森林算法(Random Forest,RF)建立蓄积量反演模型。随着遥感技术、机器学习算法和神经网络技术的发展,森林蓄积量的估测正朝着多源、非线性回归模型的趋势发展。在数据源方面,高分遥感数据、雷达数据、数字高程模型数据得到了广泛的运用。在森林蓄积量估测方法方面,各种传统的多元线性回归方法得到不断的改善,机器学习方法逐渐渗透到森林蓄积量的研究。应用精度更高的多源数据以及合适的回归模型对森林蓄积量进行估测成为了森林蓄积量估测的持续重点和难点。选择合适的森林蓄积量影响因子和森林蓄积量估测算法,不仅对精确估算森林蓄积量有着重要的意义,也对提高森林资源监测效率有着很大的影响。本研究引入Boruta特征选择方法[9]结合极端随机树(Extremely Randomized Trees,Extra-trees)方法,基于高分二号(GF-2)遥感影像数据、数字高程模型(Digital Elevation Model,DEM)数据以及森林资源二类调查数据,对龙泉市部分区域小班的每公顷蓄积量进行估测,并与随机森林(Random Forest,RF)方法[10]和梯度提升(Gradient Boosting)方法[11]进行性能对比,为快速估测县域尺度森林蓄积量提供新的方法和思路。

1 材料与方法

1.1 研究区概况

龙泉市位于浙江省西南部的浙闽赣边境(27°42′～28°20′N,118°42′～119°25′E),属于中亚热带季风气候区,温暖湿润、四季分明、雨量充沛、气候宜人,年日照时数为1 849.8h,年降水量为1 699.4 mm,年相对湿度为79%,无霜期为263d[12]。龙泉市是浙江省的重点林区,素有“浙南林海”之称,森林覆盖率高达84.3%,森林面积达到25.72万hm2,蓄积量达到1 912万m3,占丽水市的总森林面积的17.5%。

1.1 研究数据

本文的研究数据来源于龙泉市2017年森林资源二类调查数据(以下简称“二调数据”)、2009年龙泉市数字高程模型(DEM)数据和龙泉市2016年8月16日的一景高分二号(GF-2)遥感影像数据。本文研究的GF-2数据只用到其多光谱影像数据。

本文的估测指标为单位蓄积量(m3/hm2),研究单元为森林资源小班。考虑到森林蓄积量的影响特征以及参考前人的研究[13-15],本文从二调数据中获取土层厚度(TU_CENG_HD)、腐殖质厚度(FU_ZHI_HD)、年龄(NL)和郁闭度(YU_BI_DU)等4个自变量因子；从DEM数据中提取海拔(HAI_BA)、坡度(PO_DU)和坡向(PO_XIANG)等3个自变量因子；从GF-2数据中提取蓝色波段(BAND_1)、绿色波段(BAND_2)、红色波段(BAND_3)和近红外波段(BAND_4)等4个波段因子。通过对波段因子的计算,得到归一化植被指数(Normalized Difference Vegetation,NDVI)、比值植被指数(Ratio Vegetation Index,RVI)、增强型植被指数(Enhanced Vegetation Index,EVI)、差值植被指数(Difference Vegetation Index,DVI)、土壤调节植被指数(Soil-Adjusted Vegetation Index,SAVI)等5个植被指数。所有上述因子数据提取后,都集成到森林资源小班记录中,剔除蓄积量为零后的小班数据共4 002个,作为本研究的数据集参与后续实验,从中随机抽取90%的小班数据共3 602个,作为训练集数据,剩余的10%的小班数据共400个作为测试集数据。

1.1 Boruta特征选择方法

特征选择是从初始特征中按照一定的准则或方法选出部分特征,因此,被选出的特征集合必然是原始特征集的子集,保留原始特征的物理意义。Boruta特征选择方法的目标是选出所有与因变量相关的特征集合,从而更全面地理解因变量的影响因素。Boruta特征选择方法的主要步骤如下:

1) 创建阴影特征:对于每个真实特征R,随机打乱特征顺序,得到阴影特征矩阵S,拼接到真实特征之后,得到新的特征矩阵N=[R,S]。

2) 用新的特征矩阵N作为输入,训练模型(可选随机森林方法、极端梯度提升方法等),得到真实特征和阴影特征的重要性。

3) 取阴影特征矩阵S中重要性的最大值S_max,真实特征矩阵R中的重要性大于S_max的特征,记录一次命中。

4) 利用3)中的真实特征累计命中,标记特征重要或不重要。

5) 删除不重要的特征,重复步骤1)—4),直到所有特征都被标记。

最终所有的特征变量得到确认或拒绝,或者算法到达模型运行的规定限制时,算法停止[16],因此,最终的特征集被分为两种类型:被确定和被拒绝。

1.1 极端随机树方法

极端随机树(Extremely Randomized Trees,Extra-trees)方法是在2006年由Pierre Geurts等学者经过大量的实验研究之后提出的一种机器学习方法[17]。它是随机森林方法的一个变种,原理基本和随机森林一样,通过集成多个决策树进行打分,根据各个决策树预测值的平均值来进行投票。极端随机树方法的核心如下:

1) 选择样本。极端随机树方法的每个子决策树采用原始数据集训练。

2) 选择特征。极端随机树方法随机选择一个特征值来划分决策树。

3) 构建决策树。在形成决策树的过程中,每一个节点都要按照步骤2)进行分裂,直到无法再分裂为止。

4) 极端随机树预测。通过步骤1)—3)的迭代执行,建立大量的决策树,进一步构成森林。把测试样本输入到森林中,利用每一株决策树对测试样本进行分类或者回归,得到最终的分类或者回归估测结果。

由于极端随机树方法是基于随机选择特征点进行划分的方法,最终得到的决策树规模大于随机森林生成的决策树,但泛化能力强于随机森林。

1.1 模型评价

本研究选取交叉验证Cross Validataion(CV)的方式来检验模型的精度。交叉验证常用的方法有留一交叉(LOOCV)和K折交叉验证(K-fold CV)。K-fold CV是将数据集分为K个子集,并在K个子集中取一个作为验证数据集,其余的K-1个数据集作为训练集,计算所得的K个模型的预测精度的平均值作为最终的精度值。本研究采用十折交叉验证法。常用评价指标有决定系数(R-squared,R2)、均方根误差(Root Mean Square Error,RMSE)、平均绝对误差(Mean Absolute Error,MAE)、平均百分比误差(Mean Absolute Percentage Error,MAPE)和估测精度(Prediction accuracy,P)。计算公式如式(1)—(5)所示。

(1)

(2)

(3)

(4)

(5)

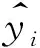
2 结果与分析

2.2 Boruta特征选择结果

本研究选取随机森林方法对Boruta进行训练,最终得到的特征选择结果(表1)。从表1中可知,经过Boruta特征选择,被拒绝的特征有腐殖质厚度(FU_ZHI_HD)、蓝色波段(BAND_1)、绿色波段(BAND_2)、红色波段(BAND_3)、近红外波段(BAND_4)、归一化植被指数(NDVI)、比值植被指数(RVI)、增强型植被指数(EVI)、差值植被指数(DVI)、土壤调节植被指数(SAVI)等10个特征,而最终被选择的特征集包含了土层厚度(TU_CENG_HD)、年龄(NL)、郁闭度(YU_BI_DU)、海拔(HAI_BA)、坡度(PO_DU)和坡向(PO_XIANG)等6个特征。

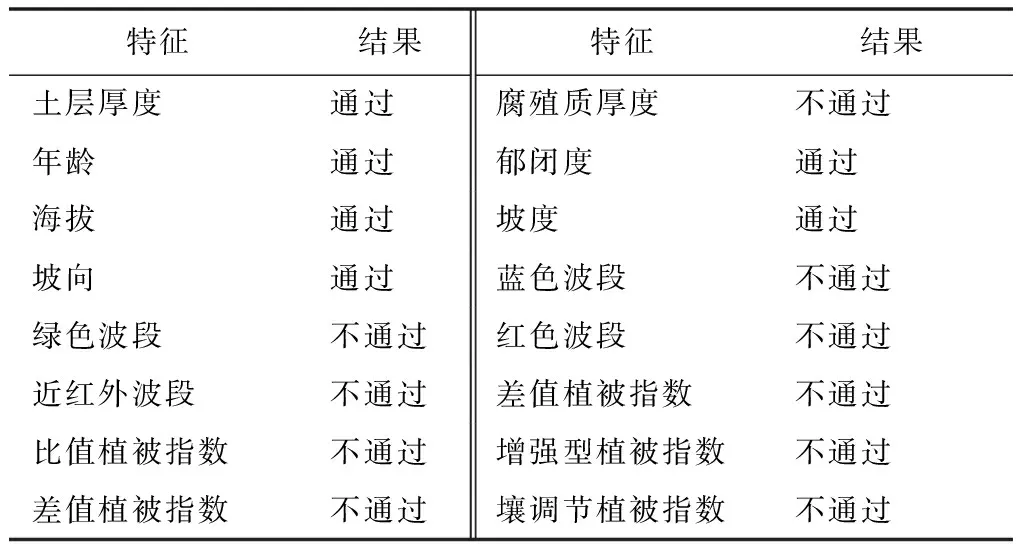
表1 Boruta特征选择结果表Tab.1 Boruta feature selection result table

2.2 模型参数优化结果

以往研究表明,参数优化对于建模具有重要意义。本研究选用3种机器学习方法(随机森林方法,Gradient Boosting 方法,极端随机树方法),参考现有文献以及反复实验设置各方法对应的参数,在此基础上对比参数调整过程中对建模精度的影响。

本研究在python环境下运行,每个方法的参数如下:

1) 随机森林方法。其基本参数为:树的个数N,设置为(50,100,150,200,250)；树的最大深度M,设置为(2,6,10,14,18)。

2) Gradient Boosting 方法。其基本参数为:树的个数N,设置为(50,100,150,200,250)；树的最大深度M,设置为(2,6,10,14,18)。

3) 极端随机树方法。其基本参数为:树的个数N,设置为(50,100,150,200,250)；树的最大深度M,设置为(2,6,10,14,18)。

本研究采用网格搜索对模型参数进行优化,通过比较不同参数对负均方误差neg_m的影响,负均方误差大的模型较优,从而得出模型最优参数,结果如表2所示。由表2可知,随机森林方法的负均方误差neg_m最大为-5.82,最优参数组合为树的个数N=150,树的最大深度M=14；Gradient Boosting方法负均方误差neg_m最大为-6.03,最优参数组合为树的个数N=50,树的最大深度M=6；极端随机树方法负均方误差neg_m最大为-5.71,最优参数组合为树的个数N=250,树的最大深度M=14。因此,本研究采用以上3种模型的最优参数分别建立森林蓄积量估测模型。

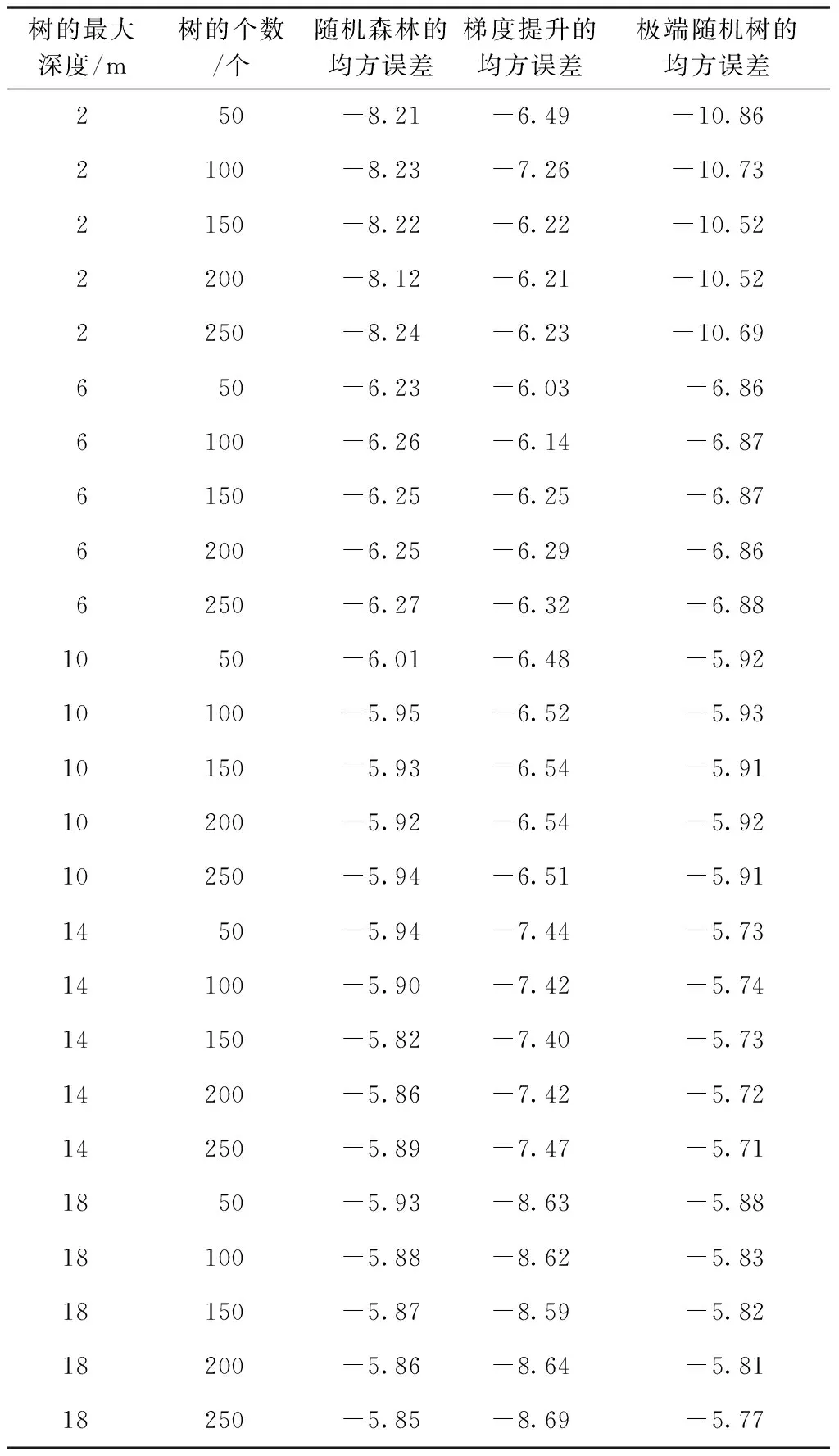
表2 网格搜索参数优化结果Tab.2 Grid search parameter optimization results

2.2 蓄积量估测模型建立

本研究的建模过程如下:基于上述Boruta特征选择结果,选择随机森林(RF)方法、梯度提升(Gradient Boosting)方法和极端随机树(Extra-Trees)方法通过网格搜索调参结果对森林蓄积量进行建模与估测。3种方法的森林蓄积量建模与估测结果如表3、图1和图2所示。

图1 3种方法蓄积量建模结果Fig.1 Three methods of accumulation volume modeling results 90

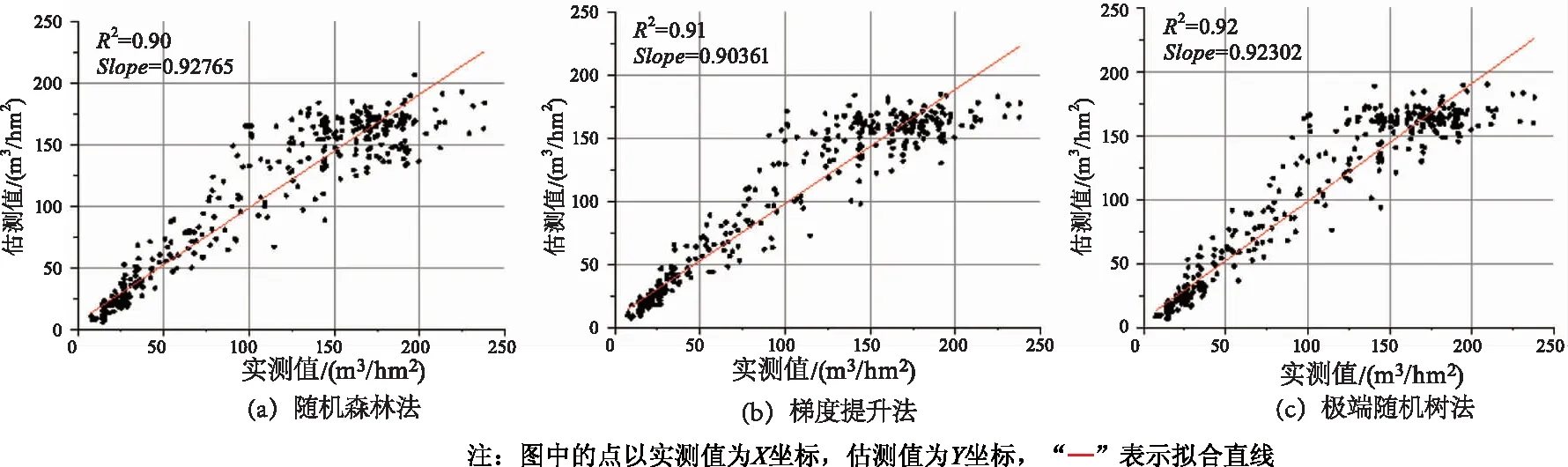
图2 3种方法蓄积量估测结果Fig.2 Accumulation estimation results of three methods

由表3可知,从建模结果看,随机森林(RF)方法建立的蓄积量估测模型的决定系数R2、均方根误差RMSE、平均绝对误差MAE分别是0.71、36.90(m3/hm2)、25.65(m3/hm2),其平均百分比误差MAPE以及估测精度P分别为13.78%和86.22%；梯度提升(Gradient boosting)方法建立的蓄积量估测模型的决定系数R2、均方根误差RMSE、平均绝对误差MAE分别是0.71,36.75(m3/hm2),25.95(m3/hm2),其平均百分比误差MAPE以及估测精度P分别为27.92%和72.08%；极端随机树(Extra-Trees)方法建立的蓄积量估测模型的决定系数R2、均方根误差RMSE、平均绝对误差MAE分别是0.73,35.85(m3/hm2),25.05(m3/hm2),其平均百分比误差MAPE以及估测精度P分别为14.05%和85.95%。从估测结果看,极端随机树(Extra-Trees)方法的决定系数R2最大、均方根误差RMSE最小、平均绝对误差MAE最小、平均百分比误差MAPE最小、估测精度P(84.14%)最大；随机森林(RF)方法和梯度提升方法的估测效果差异不明显。

表3 3种方法蓄积量建模与估测评价指标Tab.3 Three methods of volume accumulation modeling and estimation evaluation indicators

3 讨论

1) 本研究采用Boruta特征选择方法对可能影响森林蓄积量估测的特征因子进行筛选,筛选得出的特征集包括土层厚度、年龄、郁闭度、海拔、坡度和坡向等6个特征。Boruta特征选择该方法虽然损失了部分细节信息,但通过去除多因子之间相关性后起到了降维作用,从而有效减少了特征的数量,提高了建模与估测的效率及模型的泛化能力。

2) 本研究率先将极端随机树方法引入到森林蓄积量估测中,采用网格搜索调参得到模型最优参数,在不区分优势树种的情况下,最终得到的森林蓄积量的估测精度达到84.14%。李世波等[18]利用随机森林方法对湖南省醴陵市的森林蓄积量进行估测,得到的估测精度为83.69%；罗蜜等[19]采用多元逐步回归构建的福建省三明市将乐国有林场的杉木蓄积量估测精度为80.67%；李亚东等[20]采用最小二乘法结合无人机航摄影像三维点云得到的蓄积量的估测精度为82.46%。相比而言,本研究的极端随机树方法的估测精度更高，从决定系数的大小来看,本文所建模型的R2为0.73,优于郎晓雪等[21]基于支持向量机对香格里拉市云冷杉建立蓄积量模型的R2为 0.67,陈新云等[22]采用多元线性回归建立的森林蓄积量模型的R2为0.694,以及曹霖等[23]基于随机森林方法建立的吉林省中东部森林蓄积量模型R2为0.592 5。由此表明，基于Boruta特征选择方法结合极端随机树方法所建立的森林资源蓄积量估测模型具有更强的泛化能力和稳定性。

4 结论

本文基于浙江省龙泉市森林资源二类调查数据、高分二号(GF-2)遥感影像数据、数字高程模型数据提取多元特征组成原始特征集,应用Boruta特征选择方法和极端随机树(Extremely randomized trees,Extra-trees)方法,以小班为研究单元,估测龙泉市部分区域森林资源的每公顷蓄积量。结果表明，经过Boruta特征选择出的特征有土层厚度、年龄、郁闭度、海拔、坡度和坡向等6个因子,极端随机树方法采用网格搜索之后的最优参数组合为:树的个数N=250,树的最大深度M=14,测试精度为84.14%,R2为0.92,RMSE为19.65m3/hm2,MAE为13.95m3/hm2,模型优于随机森林方法和梯度提升方法,为精确估算森林蓄积量提供了新的方法。后续将考虑将本文研究结果尝试应用于不同时期不同区域的森林蓄积量估测。