古尔班通古特沙漠南缘梭梭林分距离结构模拟

汪少华,黄炳智,牛攀新

(1.湖南文理学院,湖南 常德 415000； 2.石河子大学农学院,新疆 石河子 832000；3.广西盛麒科技有限公司,南宁 530000)

林分距离结构模型不仅可以提供林分林木的距离信息,而且能为林分监测、林分重建、林分生长检测提供基础信息。目前,有关林分分布方面的研究主要集中在林分直径的静态分析[1-5]和动态分析[6-7],以及直径和年龄结构[8-9]方面的研究,研究方法上分为静态拟合和动态拟合[10-11],但关于林分的距离结构分布的研究还相对较少。梭梭(Haloxylonammodendron(C.A.Mey.) Bunge),是藜科、梭梭属的小乔木,主要分布区域为中国、中亚和俄罗斯西伯利亚,高1～9m,树杆地径可达50cm,树皮灰白色,木材坚而脆。在抗旱、抗热、抗寒、耐盐碱等方面都有很强的适应性,同时又具有生长迅速,枝条稠密,根系发达,防风固沙能力强等特点,是作为防治我国西北地区沙漠化及干旱荒漠地区固沙造林的优秀树种[12]。因此,研究梭梭林分的距离结构分布特征对于治理沙漠化和固沙造林都具有现实意义。

研究林分距离结构的分布有助于量化地描述森林结构与多样性,进而评价和对比不同林分、森林类型和森林生态系统,它是描述与构建森林空间结构的基础研究方法。林分空间结构的分析与重建已成为林业生产实践中森林生长模拟器最重要的基石,在对林分空间结构的分析与重建方法中,或者直接需要待重建林分的距离信息,或者需要事先拟合与树种有关的距离函数。然而,在林业调查实践中,这种可用于树种距离参数化的数据是有限的,因此,建立与树种有关的预估距离的模型势在必行。林分空间结构指标是林分量化不可缺少的因素,通常应用概率分布模型对这些结构特征进行研究,林业上常用的是Weibull分布模型等。目前,国内外在林分直径、树高及年龄结构的研究上普遍使用Weibull函数模型进行模拟,而对林分距离结构的概率分布模型研究较少。因此,本研究主要探讨用满足概率模型基本特征的两参数Weibull分布模型描述梭梭林分的距离结构,通过对梭梭样地林木的空间点格局分析,提取林木间的最近邻距离,确定最近邻距离分布的概率模型并对其进行参数估计,以此建立梭梭林木的距离结构概率分布模型,从而为荒漠梭梭林的距离结构模拟提供方法支持。

1 材料与方法

1.1 研究区概况

研究区位于石河子市103,148,149,150团,平均海拔为360m,地形相对平坦。石河子冬季寒冷且长,最低温度为零下35℃,夏季酷热而短,最高温度为40℃,属典型的温带大陆性气候。又因新疆位于亚欧板块中部远离海洋,故形成了干旱少雨的现象(石河子年降水量为125.0～207.7mm之间)。根据梭梭天然林在准葛尔盆地不同沙漠地形中的分布特点,分别选择103,148,149,150团4个地点,按照沙丘间地、沙丘坡上以及沙丘顶上3种生境选取150m×50m典型样地,共计10块样地进行实测。对每个样地梭梭进行每木测径,纪录各样地梭梭密度、基径及株高等状况。研究区内梭梭样地采集信息如表1所示,其中D代表梭梭基径,H代表梭梭株高。

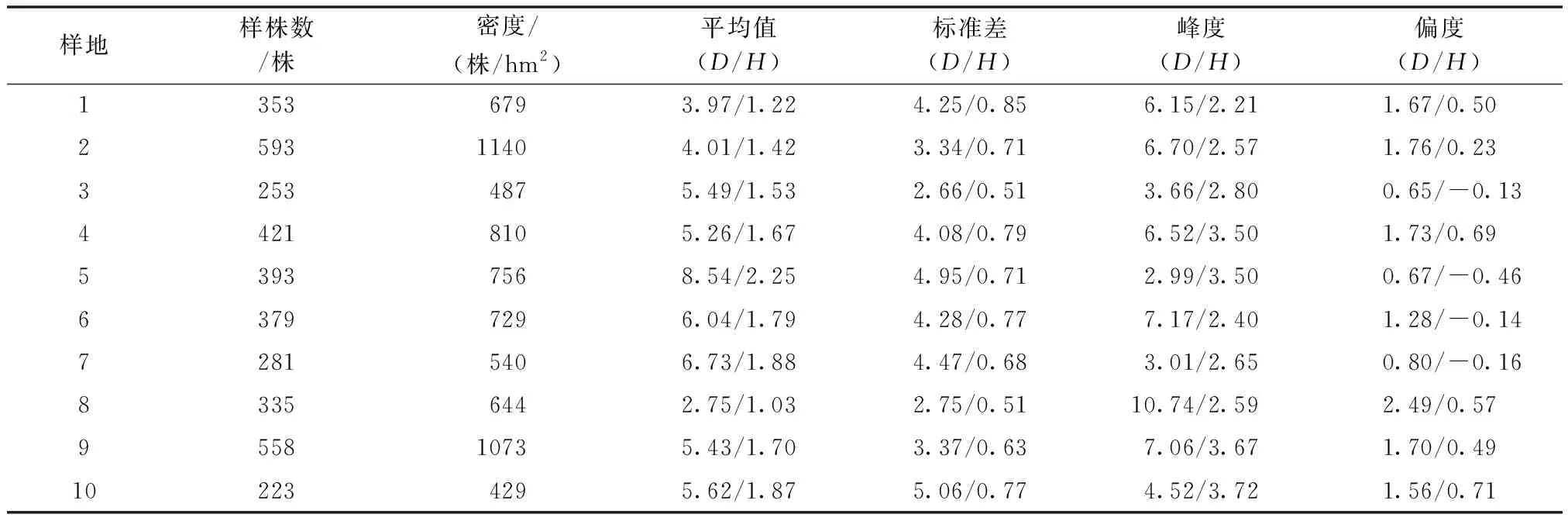
表1 研究区梭梭样地采集数据Tab.1 Data collection of Haloxylon ammodendron in study area

1.2 研究方法

本文通过Weibull-2模型来对石河子103,148,149,150团的10块梭梭样地距离分布结构进行模拟。Weibull分布函数的3个参数分别为位置参数、尺度参数和形状参数,其中位置参数a表示最小可能邻距离,因此在本次研究中位置参数a可以视为0,在此假设随机变量X(梭梭间最短距离)服从Weibull-2分布(X～weibull(b,c)),其概率密度函数为[13]:

(1)

式中:θ=(b,c),x,b,c分别为最近邻距离、尺度参数、形状参数。

两参数Weibull分布密度函数的累积概率分布为[14-15]:

f(x,θ)=1-e-[x/b]c

(2)

由累积概率分布函数可以对各距离区间的目标株数进行估计。

使用Matlab R 2016a软件对模型参数进行拟合,其中x为梭梭间最近邻距离,最近邻距离采用最小二乘法进行参数估计,拟合结果采用RMSE(均方根误差)、R2(拟合优度判定系数)进行模型适合程度检验。

(3)

(4)

(5)

(6)

式中:SSR为预测数据与原始数据均值之差的平方和,SST为原始数据和均值之差的平方和。

Kolmogorov-Smirnov(K-S)检验是比较一个频率分布f(x)与理论分布g(x)或者两个观测值分布的一种非参数检验方法,在本研究中用来检验分布的拟合是否服从原定假设,即随机变量X(梭梭间最短距离)是否服从Weibull-2分布(X～weibull(b,c))。

2 结果与分析

2.2 梭梭最近邻距离分布结构

天然林分的分布大致上分为均匀分布、随机分布和团状分布3种,为了更好地建立与梭梭实际分布情况相符的预估距离的模型,本研究首先采用Stochastic Geometry 4.1软件随机生成50m×50m范围内3种分布的模拟林分,每种分布随机生成10个,共计30个模拟林分,然后对模拟林分进行距离分布的拟合及分析。具体模拟林分最近邻距离分布结构如图1所示。

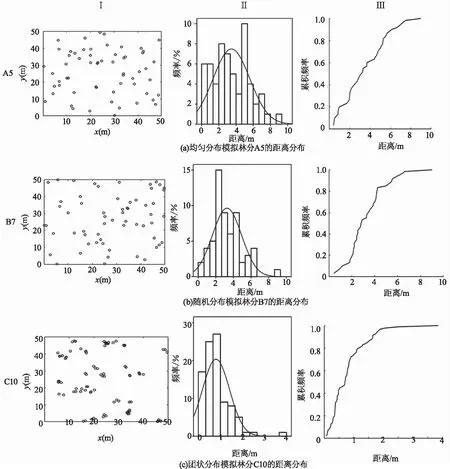
图1 模拟林分最近邻距离分布Fig.1 Nearest distance distribution of simulated stands

图1是以30个模拟林分中的均匀分布A5、随机分布B7以及团状分布C10这3个模拟林分为例,通过水平点格局(I)、频率分布(II)、相对累计频率(III)对模拟林分进行最近邻距离分布情况分析,其中A5表示样地序号为5的均匀分布模拟林分,B7表示序号为7的随机分布模拟林分,C10表示序号为10的团状分布模拟林分。

本研究选择103,148,149,150团4个地点,按照沙丘间地、沙丘坡上以及沙丘顶上3种生境选取150m×50m典型样地共计10块样地进行梭梭每木检尺,根据样地实测数据进行梭梭林分最近邻距离结构模拟。具体实测林分最近邻距离分布结构如图2所示。图2选取的是10个实测林分中的部分林分最近邻距离的水平点格局(I)、频率分布(II)、相对累计频率(III)图,其中序号2,8,9,10分别表示实测梭梭样地序号,按照梭梭林分最近邻距离的水平点格局(I)、频率分布(II)、相对累计频率(III),对实测梭梭样地林分进行最近邻距离分布结构的分析。图1和图2中的散点图可以看出,模拟的3种不同分布类型的林分分布在天然梭梭林分中都有存在。图2中,实际梭梭林分分布更多的是随机分布和团状分布结构,说明天然梭梭林分较为紧密。可以看出在1～2.5m处实际梭梭林分最近邻距离出现峰值,模拟数据中随机分布与之较接近,随机分布和均匀分布的模拟林分最近邻距离分布都较为均匀。

图2 实测林分的最近邻距离分布Fig.2 Nearest neighbor distance distribution of measured stands

通过比照模拟林分与实测林分的最近邻分布结果,可以看出实测梭梭林分的距离结构在频率分布曲线上,与模拟林分中的随机分布、团状分布的林分具有相似的趋势,表明本研究中的实测林分多呈随机或团状分布,同时也说明了模拟林分与实测林分距离分布较吻合,表明了通过计算机技术可以在一定程度上实现梭梭模拟林分与实际林分相匹配,可为森林生长模拟器的相关研究提供依据。从相对累积频率分布上看,实测林分与模拟林分中的随机林分累积频率分布趋势更加吻合,表明实测梭梭林分大多数呈随机分布,可以选择随机分布的模拟林分来反映实际梭梭林分距离结构。

2.2 模拟林分距离分布拟合检验

Weibull-2函数的尺度参数和形状参数是描述Weibull-2分布曲线最重要的参数,本研究通过模拟生成林分和实际调查林分的参数对比,以及模型曲线拟合程度对比,可以直观地分析出两者的相似程度和与Weibull-2函数的拟合程度。本文采用Stochastic Geometry 4.1软件随机生成50m×50m范围内的30个模拟林分,使用Matlab R 2016a软件计算模拟林分的最近邻距离,并用Kolmogorov-Smirnov(K-S)检验进行分布检验。分布检验结果如表2所示。

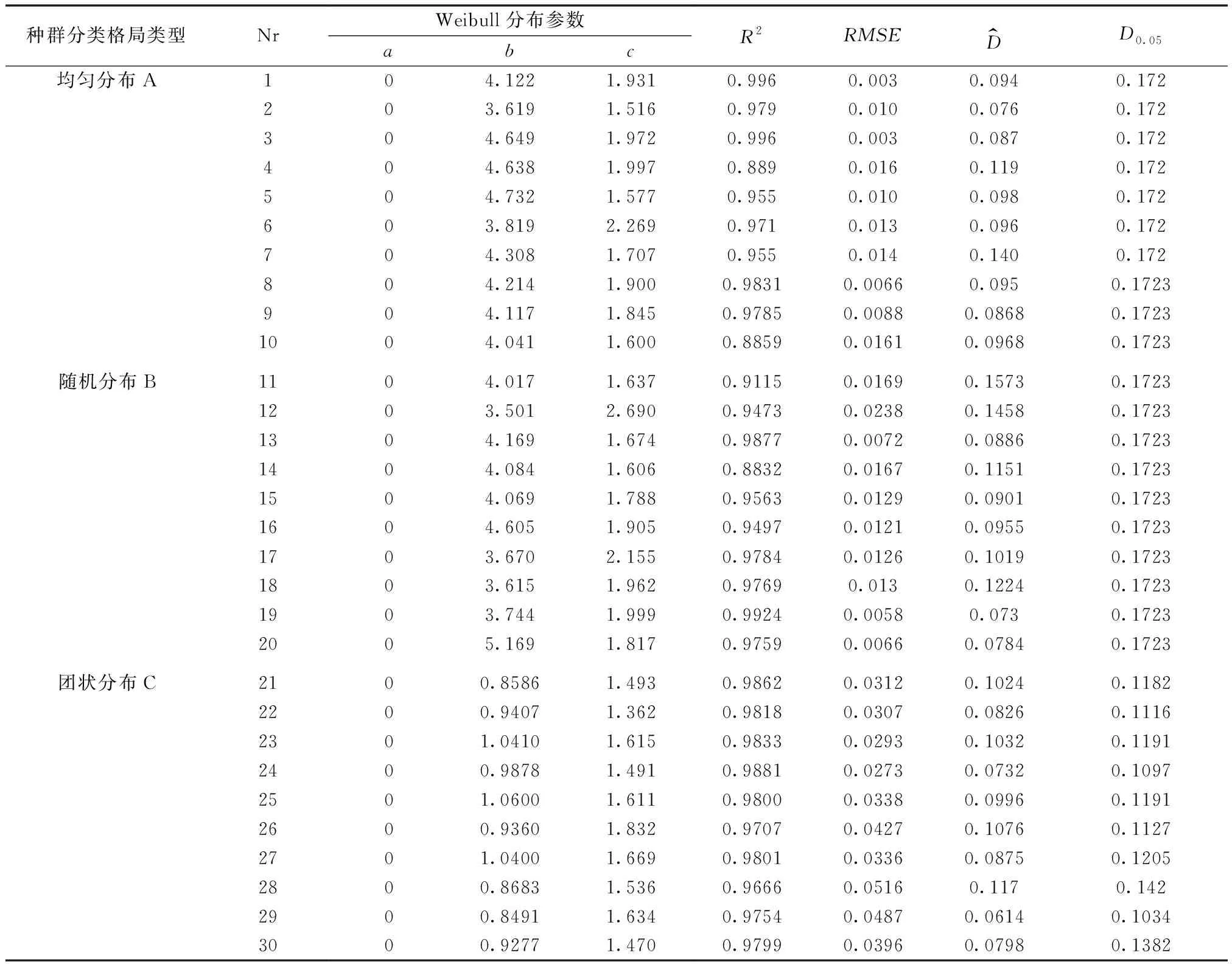
表2 模拟林分最近邻距离分布模型参数值Tab.2 Parameter value of nearest neighbor distance distribution model for simulated stands

在Weibull函数3个参数中,形状参数c是关键参数,c值主要用于描述Weibull函数的分布情况。由表2的拟合结果可知,均匀分布的b值范围为3.619～4.732,c值范围为1.516～2.269；随机分布b值范围为3.501～5.169,c值范围为1.606～2.69；团状分布b值范围为0.849 1～1.06,c值范围为1.362～1.832。一般 Weibull分布参数b值越大,密度函数曲线越平缓,顶点离x轴的距离越小；参数c的取值范围为1～3.6,当c<1 时,为倒J型分布；c=1时,为指数分布；c=2时,为x2分布；c=3.6时,近似正态分布；c→∞时,变为单点分布。

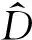
2.2 实测林分距离分布拟合检验

使用Matlab软件对10组梭梭样地实测数据进行最近邻距离的计算,拟合其Weibull函数参数并使用K-S检验对其进行Weibull-2分布检验。数据检验结果如表3所示。

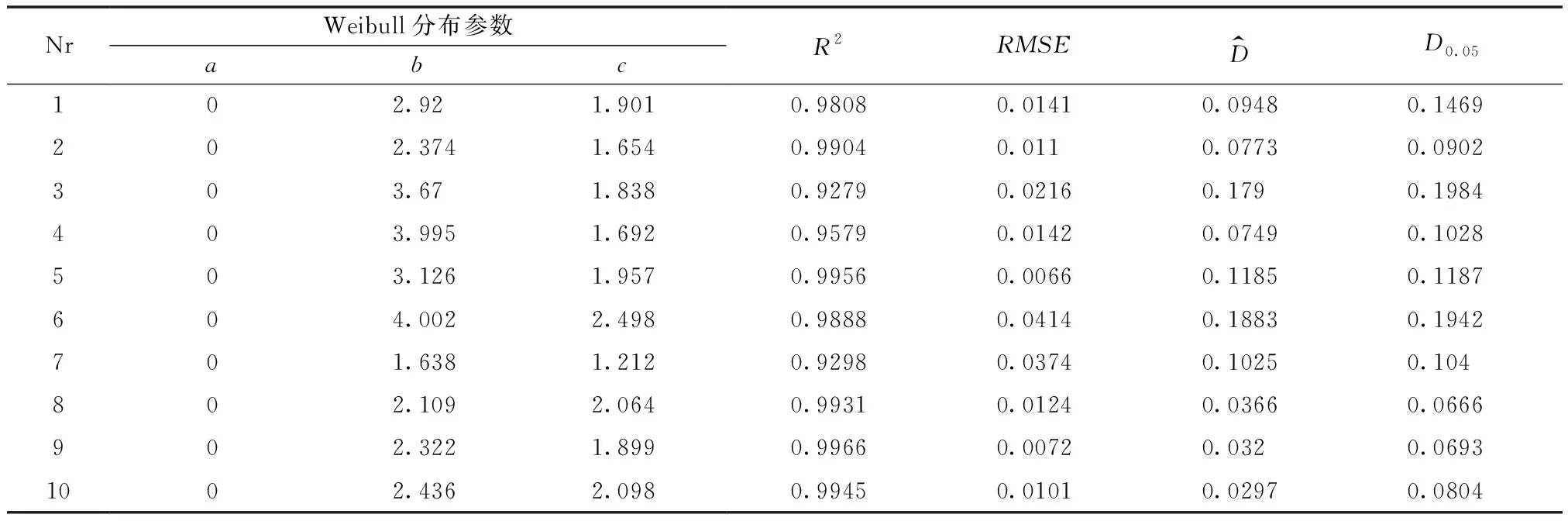
表3 实测林分最近邻距离分布模型参数值Tab.3 Parameter value of the nearest neighbor distance distribution model of measured stands

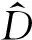
图3显示了2,5,8,9,10号5个样地的梭梭距离分布观测值与模型拟合曲线,其中x为最近邻距离,单位为m,y为落在对应x上的概率,可以看出,Weibull-2函数拟合效果与实际观测值分布趋势相吻合,模型拟合的RMSE值均较小,在0.01～0.05范围波动,拟合结果的R2值均高于0.8,说明采用Weibull-2对梭梭的距离分布进行拟合可以取得较好的效果。

由图3可以看出,样地总体的距离分布在2m附近达到峰值,即样地总体中大部分梭梭近邻距离集中在1～3m范围内,揭示了梭梭在荒漠中的个体株间距大致分布情况,其中,2,5,8,9,10号样地的梭梭距离分布均集中1～3m范围内,除了5号样地距离分布的峰值大于2m,其余样地的梭梭距离分布峰值均出现在小于2m附近,原因可能是5号样地的大径阶梭梭占比多所导致。

图3 实际数据拟合曲线图 Fig.3 Fitting curves of actual data

与计算机模拟林分的拟合结果相比,模拟数据曲线和Weibull-2函数拟合曲线的峰值较为一致,其中也会出现实际林分数据的曲线峰值高出Weibull-2拟合曲线峰值的情况,但模拟林分拟合分布情况与实际分布大体上较为吻合,说明实际梭梭林分的距离结构是一种相对紧密的结构。考虑到模拟数据是相对理想的数据,与实际情况会存在偏差,但从总体的拟合结果来看,利用Weibull-2对实际林分和模拟林分的拟合效果都是较好的,说明可以用Weibull-2分布来描述荒漠梭梭林分最近邻距离的分布情况。

3 结论与讨论

本文采用了计算机模拟与现实数据相对比的方法,通过对模拟和实际林分的距离结构图的分析和Weibull-2函数拟合情况的对比,分析林分距离结构是否能用Weibull-2分布进行描述。在模拟林分和实际林分的距离结构对比中,可以看出,模拟林分与实际林分在各个距离区间上的样本分布情况是较为相符的,模拟样地和实测样地距离分布拟合的R2值均在0.883～0.997之间,均方根误差(RMSE)取值分别在0.003～0.052与0.007～0.041之间,D值均小于D0.05值,说明了不论是模拟数据还是实际数据都符合原假设,即假设梭梭林分最短邻近距离服从Weibull-2分布,R2的值均高于0.80,RMSE的值均在0.01～0.05范围,拟合结果说明了梭梭林分的最近邻距离分布可以用Weibull分布来进行描述。

本研究梭梭林分的距离结构拟合结果表明,Weibull-2分布与3种模拟林分分布的拟合程度以及实际梭梭林分距离分布的拟合程度都较高,说明了Weibull-2分布用于描述梭梭林分距离结构的适应性较好,可以较好地描述3种常见分布的天然梭梭林分距离结构情况。这是一种能用来建立林分距离结构的分布模型,并且为以Weibull距离分布为基础,建立距离结构预估体系,提供了理论依据。总的来说,本文以梭梭天然林为例,建立其Weibull-2分布参数的距离结构模型,为今后其他树种的距离结构预测模型提供一定的理论基础。