超声速巡航导弹速度控制系统设计

邱志强,廖选平,孙瑞胜,朱 斌

(南京理工大学 能源与动力工程学院,江苏 南京 210094)

现代战争中战役战术导弹要具备大空域、多弹道、远射程、大机动的作战性能特点,超声速巡航导弹以其具有飞行包络大,能够适应各种战场需求的特点[1],成为了各个国家的研究热点之一。固体冲压发动机结构简单,质量轻,推重比大,成本低,具有较高的经济性[2],多被应用于超声速巡航导弹[3]。

清楚认识被控对象的工作特性是设计控制器的基础。从固体冲压发动机的工作原理和系统组成出发,文献[4]分析了燃气发生器的稳态和非稳态过程,通过数值模拟研究得到了自由容积和燃速压强指数对流场的影响;文献[5]通过数值模拟得到了燃烧室入口开度、燃烧室几何大小对固体冲压发动机工作的影响。针对固体冲压发动机的建模问题,学者们做了大量的研究。基于多变量变化的燃烧效率模型,文献[6]提出了发动机工作过程的模型;文献[7]则建立了一种能够对推力进行预测的燃气流量可调的固体冲压发动机模型;另外,通过影响系数法,文献[8]建立了冲压发动机的准一维模型。目前,多数研究仅针对固体冲压发动机本身,关于超声速巡航导弹速度控制系统的模型研究相对较少。

准确地控制固体冲压发动机的工作过程是超声速巡航导弹的速度控制的关键。固体冲压发动机的控制方法大多采用PID控制[9-10],但固体冲压发动机工作过程迅速,存在负调节等复杂现象[11],同时固体冲压发动机模型本身存在非线性及不确定性[12],这些都给超声速巡航导弹的速度控制系统设计带来了一定的困难,传统PID控制已不适用。因此,寻找合适的控制方法是超声速巡航导弹速度控制系统设计的关键。反演控制技术是近年发展起来的一种非线性反馈控制设计的方法。反演控制技术引入“虚拟控制量”,分别设计其控制律,最终获得系统实际的控制输入[13]。但当系统模型存在不确定性时,反演设计方法的鲁棒性能将不再满足要求。为此,国内外学者将反演控制方法结合自适应控制与滑模控制等,取得了良好的控制结果[14-16]。

本文以超声速巡航导弹为研究对象,结合固体冲压发动机的工作特性,分析并建立了超声速巡航导弹的速度控制系统数学模型。针对速度控制系统存在的参数时变和不确定干扰问题,在反演法的基础上设计了一种反演鲁棒控制器,利用Lyapunov理论验证其稳定性。通过与PID控制方法的仿真对比,验证控制器设计的可行性及有效性。

1 问题描述

1.1 速度控制系统数学模型

如图1所示,超声速巡航导弹的固体冲压发生器相当于一个固体火箭发动机,但又有别于固体火箭发动机。发动机工作过程中,由燃气发生器产生高温高速的燃气射流喷入冲压补燃室与冲压空气进行掺混增压,燃气从尾喷管喷出产生推力[17]。

图1 固体冲压发动机结构示意图

因此,为满足超声速巡航导弹的推力需求和实际的飞行条件,需要调节图1中的壅塞调节阀开度,改变发动机所产生的推力。

燃气发生器内的质量守恒方程:

(1)

式中:qm,r为燃气发生器内产生的燃气质量流量;qm,g为燃气发生器喷管排出的燃气质量流量;d(ρrVr)/dt为燃气发生器内燃气质量随时间的变化,ρr为推进剂燃烧产生的燃气密度,Vr为燃气发生器的自由容积。其中燃气发生器自由容积的变化可由推进剂燃烧减少的体积表示,即

(2)

式中:Vr0为燃气发生器初始自由容积,a为燃速系数,Sb为燃烧面积,pr为燃烧室燃气压力,n为压力指数。

将式(1)展开推导,具体过程见文献[18],可得固体冲压发动机燃气发生器内弹道方程:

(3)

在亚燃固体冲压发动机中,由于实际产生的推力不易测量且气体通过冲压补燃室的压力基本恒定[19],可将冲压补燃室的入口压力,即燃烧室燃气压力pr,经换算近似等效为推力Fp。因此有

Fp=Sipr

(4)

式中:Si为喷管面积。

超声速巡航导弹飞行速度除受推力Fp影响外,还受阻力Fx和重力G的影响,如图2所示,图中,v为超声速巡航导弹的飞行速度,α为攻角,θ为弹道倾角。

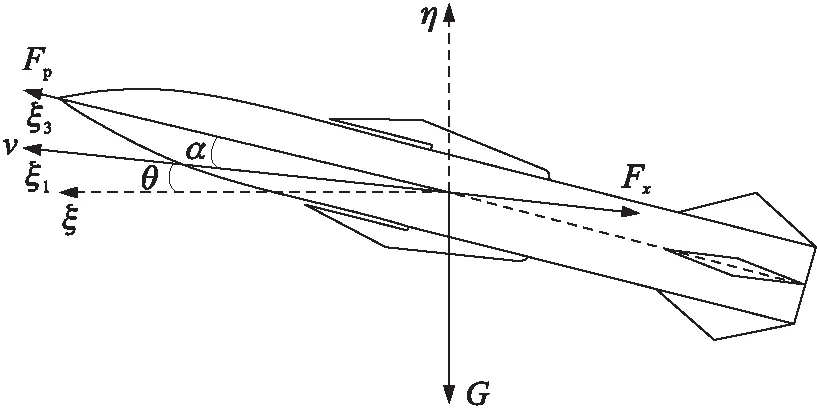
图2 超声速巡航导弹受力示意图

根据导弹的动力学关系[20],在不考虑导弹的侧向及滚转通道的情况下,导弹的纵向动力学方程为

(5)

式中:m为导弹质量。阻力Fx是由动压q、阻力系数cx和特征面积S构成的函数,表示为

Fx=cxqS

(6)

假设导弹飞行过程中做α,θ均近似为0的水平直线运动,由于动压q=ρv2/2,ρ为大气密度,式(5)可改写为

(7)

在导弹动力学关系中考虑固体冲压发动机工作特性,建立理想情况超声速巡航导弹速度控制系统的数学模型:

(8)

1.2 速度控制系统控制模型

X=(x1x2)=(vpr)

(9)

喷喉面积St作为系统控制输入量u,可以得到速度控制系统的状态空间形式:

(10)

2 控制器设计

本文设计反演鲁棒控制律的基本思路为:首先利用传统反演法的思想推导得到满足导弹飞行速度增量所需期望推力Fp,d,然后设计鲁棒控制律控制燃气发生器喉部面积St,产生趋向于期望推力的实际推力,从而跟踪速度指令vc。

2.1 速度控制器设计

对于速度控制系统(10)中子系统1,定义速度跟踪误差为e1,参考速度为x1,d,则

e1=x1,d-x1

(11)

且

(12)

定义Lyapunov函数为

(13)

对式(13)求导得:

(14)

将式(12)代入式(14)有

邹先生说，秦桧死后，陆游 “急于出仕的心迹，在这首诗中表现得最为明显” ，并将这首作于绍兴二十六年(1156)冬的诗， “不妨看作是陆游出仕前向云门的告别”。既然邹先生将这首诗看作是“告别”之作，那么绍兴二十七年(1157)春，陆游就应该出仕的了。因此，邹先生紧接着说“这里涉及《送陈德邵宫教赴行在二十韵》《朱子云园中观花》《酬妙湛闍梨见赠》《次韵鲁山新居绝句》《寄陈鲁山》等诗的编排问题，笔者(邹志方)以为，这些诗均作于出仕前，即绍兴二十六年冬日前。” ⑥然而，查钱仲联先生《剑南诗稿校注》(上海古籍出版社2005年版)，这些诗均在绍兴二十七年(1157)作于山阴。

(15)

(16)

式中:控制器可调控制参数k>0,且k∈R。定义控制系统的推力误差为e2,则

e2=x2,d-x2

(17)

且

(18)

由于传统滑模控制存在抖振现象,为避免出现抖振,本文设计如下具有高频反馈鲁棒控制的速度控制算法:

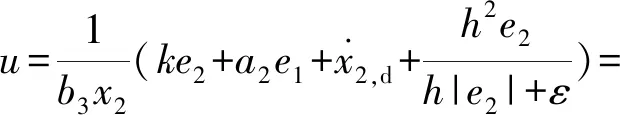
(19)

式中:控制器可调控制参数ε>0,ε∈R;h表示不确定系统的正上界函数。在该控制算法控制下,速度控制系统能够实现超声速巡航导弹的速度控制并且保证最终速度误差有界。

2.2 稳定性分析

定义Lyapunov函数为

(20)

对式(20)求导得:

(21)

将式(17)代入式(21)并展开得:

(22)

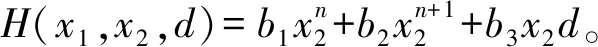
(23)

设计h,使得h≥|H(x1,x2,d)|,将式(23)进行放缩,过程如下:

(24)

由于

(25)

将式(25)代入式(24)则有

(26)

求解微分不等式(26),可以得到Ve1,e2(t)的上界:

(27)

求Ve1,e2(t)终值:

(28)

因此,将式(20)代入式(28),由Lyapunov稳定性理论知,最终系统误差满足:

(29)

由式(29)可知,当经过时间充分长后,系统误差的界与初始状态无关,即速度控制系统的误差可以达到全局一致最终有界(GUUB)。

3 仿真分析

为验证所提出的反演鲁棒控制方法的可行性及有效性,本文以某超声速巡航导弹为例设计反演鲁棒控制律进行仿真,并与传统PID控制进行对比分析研究。传统PID控制器控制律设计为

(30)

式中:kp为比例系数,ki为积分系数,kd为微分系数。

3.1 标称模型下的数值仿真

图3给出了标称模型条件下反演鲁棒控制器和PID控制器响应速度指令的曲线,图4给出了速度跟踪误差曲线,图5给出了燃气发生器自由容积变化曲线。从图中可以看出,随着时间增加,燃气发生器自由容积不断增大,速度控制系统模型参数将逐渐偏离初始时刻。PID控制系统存在明显相位滞后且由于参数变化的影响导致控制效果逐渐变差;而反演鲁棒控制能够在全过程中准确地跟踪指令信号,跟踪效果明显优于PID控制,受模型参数变化影响较小。

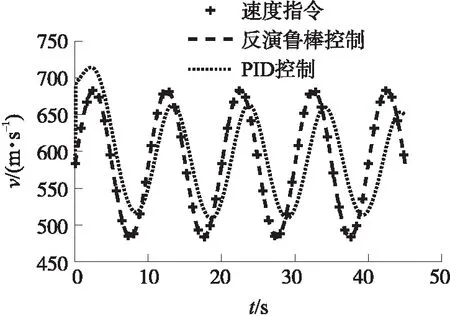
图3 标称模型下的速度响应曲线

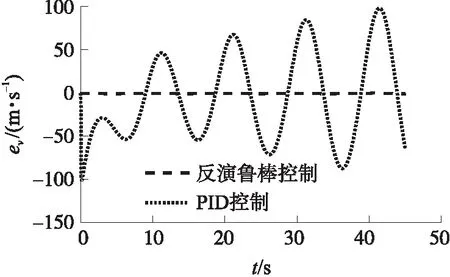
图4 标称模型下的速度误差曲线

图5 标称模型下的自由容积变化曲线

图6给出了固体冲压发动机喷喉面积变化曲线。从图中可以看出,反演鲁棒控制的控制量响应速度明显快于PID控制,并且未出现抖振现象。

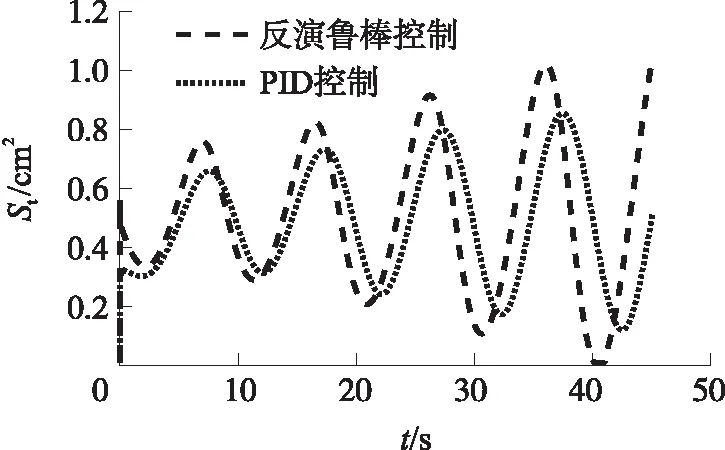
图6 标称模型下的喷喉面积变化曲线

图7、图8分别给出了固体冲压发动机压强变化曲线和流量变化曲线,由图可见,反演鲁棒控制的压强和流量变化较为快速、稳定。

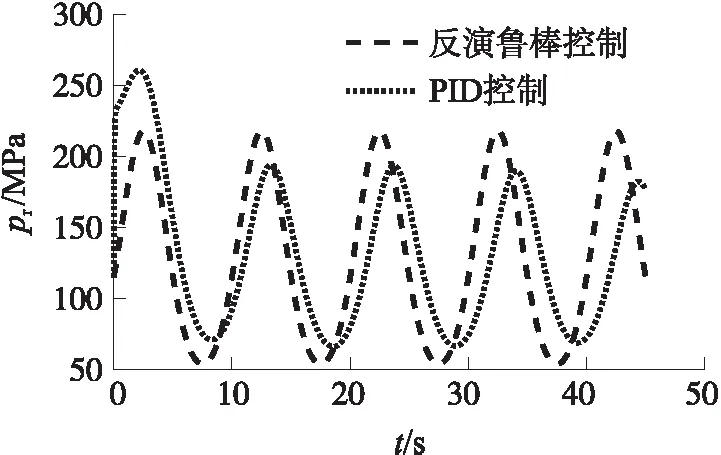
图7 标称模型下的压强变化曲线

图8 标称模型下的流量变化曲线

3.2 存在干扰的数值仿真

假定超声速巡航导弹维持匀速巡飞,v=583.2 m/s,在15 s时由于壅塞调节阀被烧蚀,喷喉面积瞬间扩大2×10-5m2。对突变的外部扰动进行模拟,图9给出了此时的速度变化曲线,图10给出了受干扰的速度误差曲线。由图可知,PID控制系统受此干扰影响,出现25 m/s的速度误差;而反演鲁棒控制系统受此干扰影响,仅产生不到0.5 m/s的速度误差,抗干扰能力明显较强。

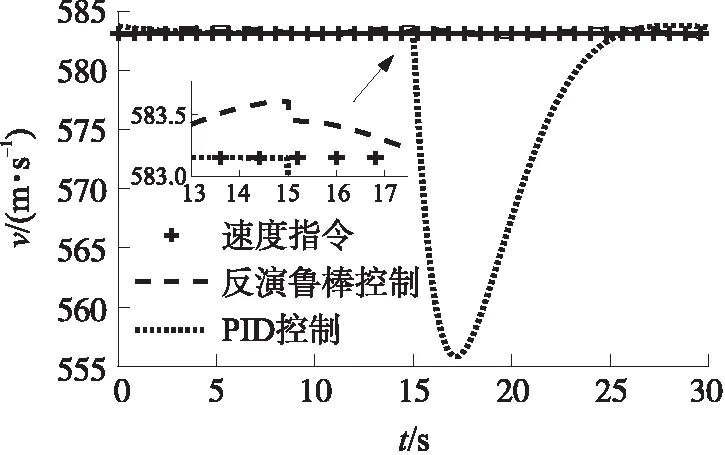
图9 受干扰的速度响应曲线

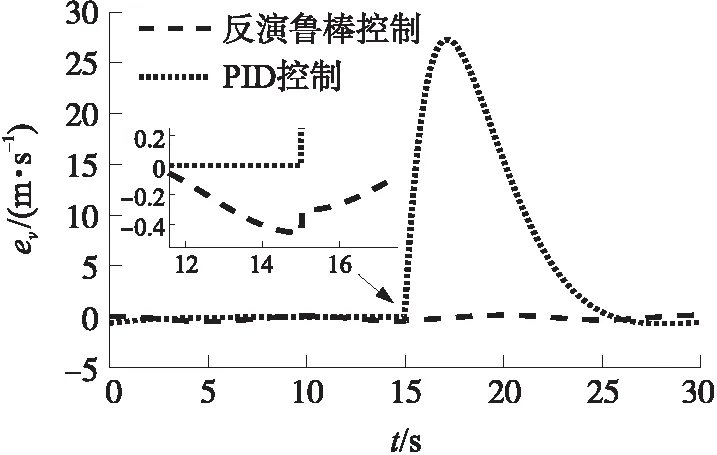
图10 受干扰的速度误差曲线

图11～图13给出了此时固体冲压发动机的工作过程变化曲线。由图可以看出,反演鲁棒控制系统在受到外界干扰后能够迅速调节喷喉面积,弥补被烧蚀部分产生的影响,使压强和流量在短时间内恢复原本状态,维持导弹巡飞速度。

图11 受干扰的喷喉面积变化曲线

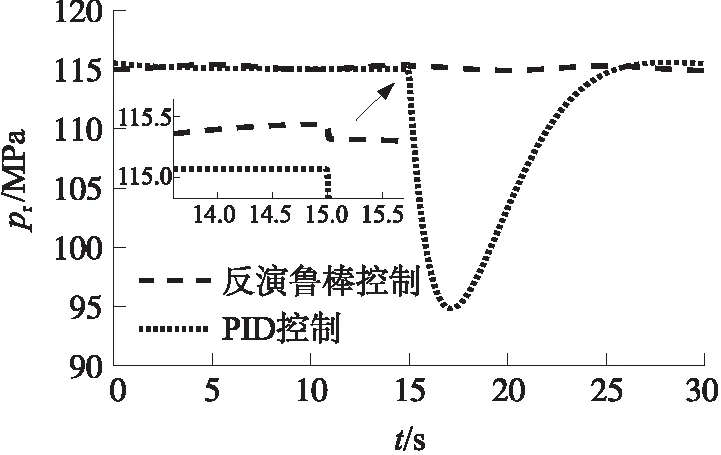
图12 受干扰的压强变化曲线

图13 受干扰的流量变化曲线

4 结论

本文根据超声速巡航导弹飞行动力学关系,结合固体冲压发动机的工作特性建立了超声速巡航导弹速度控制系统模型。由于速度控制系统存在参数时变、不确定干扰等问题,采用传统的PID控制难以满足导弹巡航过程的速度需求。本文在反演法的基础上,有效地结合了反演控制和鲁棒控制的优点,设计了复合型反演鲁棒控制器,通过模拟仿真验证其控制效果。在标称模型仿真条件下,传统控制方法速度误差达到50～100 m/s,反演鲁棒控制器控制速度误差小于0.5 m/s。超声速巡航导弹固体冲压发动机实际工作过程中响应时间较慢,仿真结果中受扰动影响速度控制系统响应时间小于0.1 s,而目前固体冲压发动机响应需要3～8 s。仿真结果表明,本文提出的控制算法能够快速精确地跟踪目标指令,同时具有较强的鲁棒性。