一种基于铜柱测量的膛内燃气最大压力计算方法

刘 涛,张领科

(南京理工大学 能源与动力工程学院,江苏 南京 210094)

常规的内弹道过程中,弹丸在火药燃气的压力推动下加速运动,完成发射过程。因此火药在膛内燃烧生成的燃气压力的变化和分布规律是内弹道学研究中的最重要参量。对膛内燃气压力的测量一直是实验内弹道学的重点研究对象。在内弹道实验中,通常采用电测压法和塑性测压法2种测压方法。其中塑性测压法以铜柱测压法为代表,亦是目前最为常用的测压方法。

使用铜柱测压法测量膛压,即利用膛内燃气压力使铜柱压缩,通过铜柱压缩量与压力表对比得到待测膛压的峰值。这种方法使用方便,操作简单,经济性好且有相当的可靠度。但由于铜柱使用静态压力标定而待测的火药燃气压力为动态加载,使得铜柱测压法总是存在一定的动、静差,即由于静态标定、动态测量所产生的误差。一般来说,铜柱压力与真实膛压峰值有20%左右的差值。常用的修正方法有:①经验修正法,②准动态标定法,③系统构建法,④预压实验法。

本文基于铜柱塑性状态的动态本构关系,以预压过程作为静态加载参考,考虑活塞惯性力的作用,建立铜柱测压器系统的数学模型,为动态误差分析建立包括预压过程在内的更为实用且简化的数学模型。

1 减少铜柱测量误差的基本原理

实践证明,测压器活塞惯性和铜柱动态本构关系是造成铜柱测压器动、静差的2个主要原因[1]:①火药燃气压力通过测压器活塞压缩测压铜柱的同时,活塞随着火药燃气向铜柱压缩方向运动,卸载时活塞由于惯性要继续运动压缩铜柱产生静差,使得压力测量值大于真实值;②塑性材料存在应变率效应,塑性材料的实际应力-应变关系与应变率有关,随着加载速度增大,应变率增大,材料的屈服极限将提高,使压力测量值小于真实值。在内弹道膛压测量实验中,材料动态本构关系的影响更大,尤其是小口径枪炮膛内动态加载速率很大,铜柱测压法测得的压力小于真实压力。本文将以铜柱应力-应变关系为基础,对实验中的数据处理方法进行改进简化。

在进行铜柱测压实验前需要对铜柱进行预压。不同批次铜柱之间,及同一批铜柱的个体之间,也存在着一定的机械性能的差异,为了对这一误差进行修正,常对出厂的铜柱使用压力机以一定压力进行一次预压,并记录预压的压力和变形量,在测量膛内压力时,根据预压时体现的铜柱“软硬程度”与同一批编表铜柱具有的平均机械性能的差异进行修正。本文通过构建铜柱的应力-应变关系,利用电子测压器测得的压力脉宽,提出一种通过数值计算获得膛压的数据处理方法,对铜柱测压结果进行修正,并借助量纲分析及相似理论进行分析,给出了某实验条件下的修正公式。该方法可以提高铜柱测压精度,更接近电子测压器,满足靶场校验时的更高精度的测量需求。

2 预压过程中铜柱的本构关系

测压铜柱常利用铜柱压力机以缓慢加压的方式对铜柱进行预压。铜柱压力机原理[2]如图1所示。

图1 铜柱压力机原理

在压力机杠杆左端有一支撑点O,右端有载荷FQ加于加载点B处,测压铜柱放在着力点A处的升降台上。没有载荷时,A点的支撑弹簧恰好能维持杠杆水平平衡。预压时在B点加上载荷FQ,并驱动升降台缓慢上升,保持杠杆水平平衡,这时铜柱就在压缩力F作用下发生塑性变形,由原始高度H0缩短为预压后高度Hb,0,如图2所示。

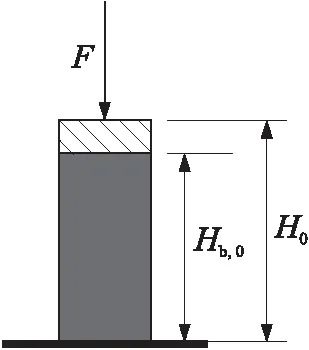
图2 铜柱受力示意图

由杠杆平衡条件可知:

(1)

在预压过程中,由于加载过程较为缓慢,整个过程可以视为准静态过程,可以使用静态标定实验得到铜柱的静态本构关系:

(2)

式中:应力σ=F/Sc,Sc为铜柱横截面积;ε为应变;E为弹性模量;Es为塑性段的弹性模量;σs为弹性极限。

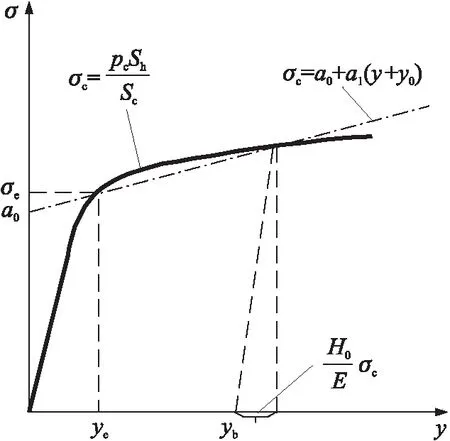
图3 铜柱静态加载曲线

(3)

根据静态压力与压后高关系表,即可通过式(3)换算σc与y的关系,该关系通常为三次多项式的形式。根据铜柱压力对照表及实验中的使用情况,在使用铜柱测压法测量膛压时,选取适当规格的铜柱的情况下,铜柱变形量与最大膛压具有良好的线性关系[3];同时,用于测压的铜柱在静态压力下的力学性能具有一定的一致性,故铜柱的静态应力-应变关系如下:

(4)

式中:y0为预压变形量,对于无预压铜柱y0=0。

测压铜柱由纯净的电解铜加工而成,含铜量不小于99.97%,软、硬机械性能及产生的变形能均匀一致,纯铜的静态弹性极限约为30 MPa,即铜柱的弹性极限σe与应变εe为定值。通过铜柱预压的变形量和预压压力即可根据式(4)得到铜柱塑性阶段的弹性模量Es及式(4)中的系数a0,a1。

3 铜柱测压系统的数学建模

3.1 基本假设

根据铜柱测压器的工作原理[2],基于铜柱测压的特点和分析方便,提出以下基本假设:

①忽略测压油管道效应和测压油的惯性影响;

②将活塞杆视为刚体而不计其变形;

③忽略铜柱内应力波的传播,在测试过程中铜柱各个截面所受应力在同一时刻相等;

④不计活塞杆受到的摩擦。

3.2 活塞运动方程

图4为铜柱测压系统简化受力模型。

图4 铜柱测压系统简化模型

活塞的运动方程:

(5)

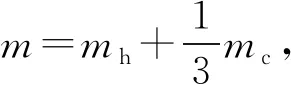
F(y,y′)=Scσ

(6)

式中:σ为铜柱动态应力。

3.3 铜柱的本构方程[4]

(7)

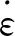
C(ε)=C1e-C2ε+C0

(8)

式中:C0,C1,C2为常数,可通过材料动态性能测试实验得出。

3.4 变形协调方程

对于预压铜柱:

(9)

3.5 铜柱静态应力-应变关系

通常根据铜柱出厂时的静态压力与压后高关系表(pc,Hb)可换算出σc与y的三次函数关系[5]。由于测压铜柱本身的力学性能具有较好的一致性[6],且在测压实验中表现出线性规律,在此可进行简化,即

(10)

上文中的三阶常微分方程初值问题可化为一阶常微分方程组的初值问题。

①弹性段。

(11)

初始条件:

结束条件:

y1(t)=ye

以此时刻参数作为塑性段初始条件,同时补充条件y3(0)=0。

②塑性段。

(12)

当已知测压铜柱的材料参数时,根据内弹道实验时铜柱的压后高Hb,t及压力脉宽即可计算得到内弹道压力峰值pm,c。计算流程如图5所示。

图5 计算流程图

4 计算分析

4.1 基本参数

文献[4]中,选用型号为φ8 mm×13 mm 1201批次的铜柱和电子测压器,在不同装药号下分别进行膛压测试实验。通过该批铜柱的压后高和压力对照表得到各种装药条件下所测压力pm,t,以电子测压器所测压力曲线得到电测压力峰值pm,e和压力脉宽tm。

本文以上述实验的结果为例进行分析,实验中所使用的铜柱力学性能参数作为计算常量,如表1所示。根据实验中获得的电测压力脉宽[7],以半正弦压力脉冲作为动态加载的压力信号,以实验中的电测压力峰值和铜柱查表压力作为参考依据,如表2所示。表中,p0为预压压力,Hb,0为预压后铜柱高度,Hb,t为实验后铜柱高度,pm,e为电测压力峰值,tm为电测压力脉宽。

表1 计算常量

表2 输入参数[3]

利用表2中的电测压力及脉宽可以确定实验中铜柱的平均加载速率范围为:74.79～131.73 MPa/ms。

4.2 计算结果

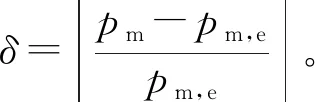
表3 铜柱测压法与模拟计算的对比

由表3可以看出,在计算压后高与实验结果相差0.003 mm以内时,仿真计算的压力峰值比通过查表获得的压力值更接近电测最大压力,误差可以减小到3%～10%,但仍存在随着被测压力增大误差也增大的问题。为了进一步减小误差与误差带,借助量纲分析及相似理论[8-10],得出经验公式:

(13)

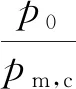
(14)

修正后的结果如表4所示,表中,p′m为修正后的压力峰值,δc为计算压力峰值相对电测压力峰值的误差,δ′c为修正后的压力误差。

表4 修正结果

修正后的误差能够被控制在±3%以内,尤其是对高压情况下的预测误差更是稳定在1.65%左右,说明在内弹道射击实验中可以通过这种数据处理方法来提高铜柱测压法的准确度。由于铜柱测压本身存在着动态响应性差的固有缺陷,上述公式中的系数仅适用于本文中的加载条件。

5 结论

本文使用铜柱测压系统的数学模型,进一步考虑了铜柱力学性能的个体差异,通过铜柱预压过程得到了铜柱的静态应力-应变关系;采用数值方法计算得到火炮膛压的峰值,借助量纲分析及相似理论对计算结果进行修正并对高压实验进行了预测,结果一致性良好。得到如下结论:

①采用本文提出的最大压力计算模型,与传统的一次预压铜柱测压法相比,不再需要借助铜柱压力表,只需要输入实验数据即可获得结果,后续可将整个铜柱测压实验中的变形量数据由激光等方式自动化测量直接导入计算机,操作更加简单;

②在74.79～131.73 MPa/ms的平均加载速率下,提出了铜柱压力修正公式(14),对高压情况下预测的压力误差显著小于传统查表方法,对靶场内弹道实验有积极意义。