基于层次分析法和熵值法的分类延迟退休问题研究
张 妍, 王海玥, 焦琳致
(辽宁师范大学 数学学院,辽宁 大连 116029)
老龄化全国委员会预测,中国60岁以上的人口预计将在2050年左右达到4.87亿的峰值,近中国人口的35%,未来中国养老压力将会异常巨大.延迟退休年限是应对人口老龄化压力的有效措施.苏春红和李齐云[1]通过对OECD代表性国家法定及提早退休年龄的分析并结合我国现状,对我国实行弹性延迟退休年龄进行制度设计.邹铁钉和叶航[2]基于养老金亏空与劳动力市场的联动效应,构建了延迟退休方案的数学模型,并对普通和分类延迟退休的经济、政治可行性进行数值模拟.王晓军和赵明[3]对人口寿命延长与延迟退休之间的关系进行探讨,测算延迟退休对我国养老金支付压力的影响.王克祥和于凌云[4]从国家政策的角度出发,对延迟退休年限政策制定的现实阻力、政策效应以及备选方案进行分析,为延迟退休年限进一步提供理论基础和配套的制度改革方案.田月红和赵湘莲[5]以我国现行的养老保险制度为基础,构建基础养老金长期财务精算模型,研究不同的渐进式延迟退休方案对我国基础养老金财务可持续性的影响.徐婷婷[6]以福建省基本养老保险基金作为研究对象,预测出现行退休政策和渐进式退休策略下养老金收支情况.刘万[7]估算了延迟退休对城镇职工基本养老金的影响.
本文采用层次分析法和熵值法相结合的方法,具体讨论了5种具有代表性群体的延迟退休方案.
1 指标评价体系的构建
从退休人员的个体考虑,从事不同种类工作的退休人员的合理退休年龄也不应相同,因此对5类群体:事业单位工作人员及公务员、专业技术人员、企业职员、轻体力劳动者、重体力劳动者进行研究,构建如表1的指标体系:

表1 评价指标体系
2 确定权重分配向量
因为层次分析法容易受到主观因素的影响,所以无法避免评价人员的主观片面性,导致该方法不能进行较高精度的过程评价.所以考虑将层次分析法与熵值法相结合,降低主观因素,如图1所示.计算步骤分别用层次分析法与熵值法求出权重,然后按照下面的式(1)进行合成.这样既充分保留了各种指标传递的信息,又可通过知识经验对客观权重加以修正.
(1)
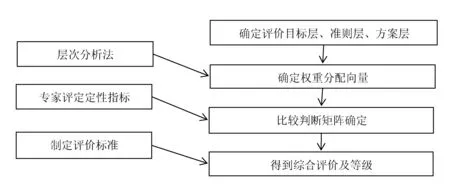
图1 评价方法模型图
首先使用层次分析法计算权重.根据本文建立的指标体系,各层次元素两两比较,构造比较判断矩阵.判断矩阵表示针对上一层次因素,本层次各因素之间相对重要性的比较,设比较的n个元素U={U1,U2,…,Un}对目标Z的影响,确定它们对Z的影响程度.每次取两个因素Ui和Uj,用aij表示Ui与Uj对Z的影响之比:
A=(aij)为比较判断矩阵,其赋值通过专家技术咨询的方法获得,见表2.

表2 判断矩阵标度及其含义影响
采取方根法计算出某层次因素相对于上一层次中某一因素的相对重要性,计算判断矩阵每一行元素的乘积:
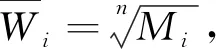

其中,(Awi)表示Aw的第i个元素.现在进行一致性检验,一致性指标和随机一致性比率分别为
其中,RI为平均随机一致性指标,可查表3得到.当CR<0.10时,通过一致性检验即确定权重分配向量为w=[w1,w2,…,wn]T.

表3 随机一致性指标RI的数值表
假设要比较的5种因素体质要求、收入情况、工作环境、受教育年限、工作经验为U={U1,U2,…,U5},通过专家技术咨询数据得到比较判断矩阵:


现在使用熵值法确定权重.定量指标可以直接给出初始值;定性指标则根据专家的经验打分,将指标分为“很好、较好、一般、较差、很差”进行模糊评价,权重分别为“9、7、5、3、1”.计算第i项指标下,第j个评价对象标值xij的比重pij,公式如下:
计算第n项指标的熵值ej,公式如下:

计算第n项指标的差异系数gj=1-ej,j=1,2,…,n,越大则指标越重要.确定指标权重:
根据式(1)可得最终的权重向量为ω=[ω1,ω2,…,ωn]T.
3 模型计算
对于从事不同种类工作的人员延迟退休年限预测问题,笔者通过层次分析法来构造数学模型,如图2.该模型的方案层为5个不同工作群体.则得到层次结构模型如下:
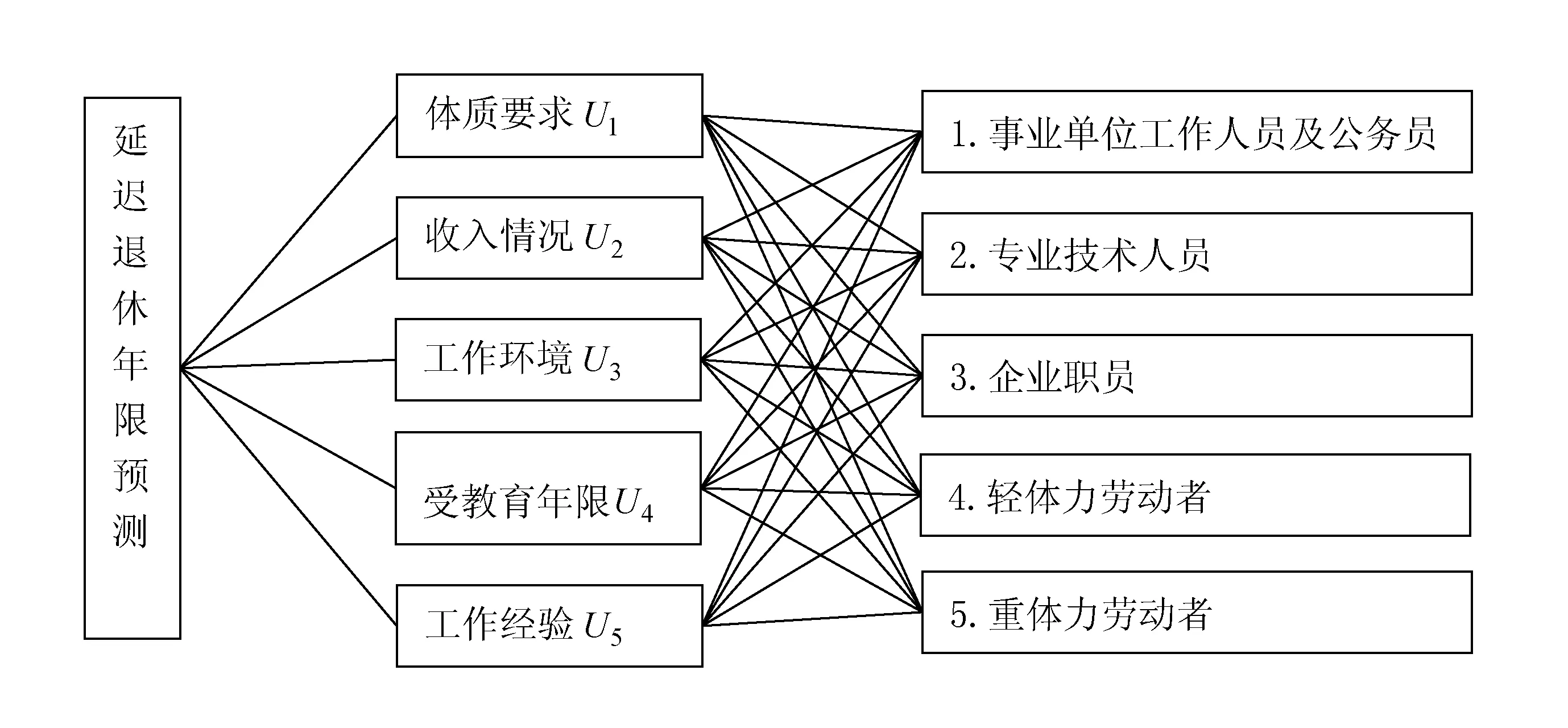
图2 延迟退休年限预测一级指标评价
现在开始方案层对准则层的分析.记准则层对目标层的权向量为w=(0.462 6,0.256 2,0.046 0,0.085 9,0.149 3)T,根据式(1)建立的模型,来求方案层对准则层的权向量.
方案层对U1(体质要求)的成对比较矩阵:
最大特征根为λ1m=5.286 6,权向量为ω1=(0.043 8,0.022 7,0.069 1,0.257 0,0.507 4)T.
方案层对U2(收入情况)的成对比较矩阵:
最大特征根为λ2m=5.938 7,权向量为ω2=(0.070 7,0.015 4,0.059 0,0.199 6,0.165 3)T.
方案层对U3(工作环境)的成对比较矩阵:
最大特征根为λ3m=5.525 0,权向量为ω3=(0.496 8,0.054 7,0.155 7,0.064 8,0.028 0)T.
方案层对U4(受教育年限)的成对比较矩阵:
最大特征根为λ4m=5.385 8,权向量为ω4=(0.154 6,0.103 0,0.256 2,0.055 9,0.030 4)T.
方案层对U5(工作经验)的成对比较矩阵:
最大特征根为λ5m=5.237 5,权向量为ω5=(0.033 3,0.112 8,0.261 5,0.129 0,0.063 4)T.
4 综合评价
通过上述的层次分析模型,对5个不同群体的延迟退休年限得到了其权重系数,其中,数值越小,表明延迟退休年限应越长.对5种不同人群进行排序如表4.

表4 层次排序结果
由表4得到了方案层的总排序权值,权重由低到高为专业技术人员、事业单位工作人员及公务员、企业职员、轻体力劳动者、重体力劳动者.如若国家出台延迟退休策略,延迟退休的年限应按专业技术人员,事业单位工作人员及公务员,企业职员,轻体力劳动者,重体力劳动者的策略安排.

