基于Mathematica 的光的干涉实验的仿真模拟

陈学文，张家伟，姚 雪，时 澄，吴思韵

（重庆科技学院 数理与大数据学院，重庆 401331）

光学实验是大学普通物理实验课程中的一个重要板块，理解光学中的科学奥秘对当代大学生认识世界具有重要引导作用。光学实验中涉及到光的干涉的典型实验有“迈克尔逊干涉仪的调整与使用”“牛顿环”和“用双棱镜测钠黄光的波长”等。此类实验理论知识抽象、调试难度大、操作时间长、测量精度要求高，学生很难在有限的学时内通过改变参数全面观察实验现象，容易造成学生的片面认识和错误判断，不利于对知识的掌握[1]。

将计算机仿真模拟应用到大学物理实验教学过程，对教学效果的提高具有积极作用。仿真模拟演示可以利用图像、动画等方式，与知识讲授同步进行，有利于学生建立起清晰直观的物理概念，更好地理解、巩固所学知识[1-2]。计算机仿真模拟可以不受仪器、场地限制，而使实验效果形象、直观，同时还可方便地改变实验参数，计算分析观察对象的相应变化，从而得到不同实验条件下的实验现象和实验结果，用来分析不同因素对实验的影响，并验证实验设想。这种教学方式有助于解决教师讲解困难、学生理解吃力问题，有助于培养学生独立探索能力、实验操作能力和科学研究兴趣[3]。

在计算机仿真模拟中，Mathematica 和Matlab 是两个常见的软件，在大学物理实验中也常用 Maple、LabVIEW 等软件进行仿真模拟[4-7]。Matlab 主要应用于工程计算、控制设计、信号处理与通信、图像处理、信号检测、金融建模设计等方面。Mathematica 拥有强大的数值计算、符号运算和图像处理功能，具有较好的图形界面，可以用各种图形、动画方式输出计算结果，实现计算机的可视化。此外，Mathematica 对公式的输入十分方便、直观，对文本格式要求低，且仿真模拟结果以 cdf 格式文件输出，可在各种安卓、iOS系统移动设备上运行，大大增加了便利性。

本文首先从理论上简要推导干涉条纹的光强分布公式，进而基于Mathematica 软件动态模拟干涉条纹，最后针对实验中两反射镜不严格垂直的实际情况，讨论此情况下的光强分布，并进行相应的Mathematica 模拟。

1 迈克尔逊干涉仪光强分布理论推导

迈克尔逊干涉仪广泛应用于长度精密计量、光学平面检验及高分辨率光谱分析等。“迈克尔逊干涉仪的调整与使用”是大学物理实验中十分重要的实验，既可以使学生直观认识光的干涉现象，又能对氦氖激光的波长进行精确测量。但是由于其理论的复杂性和知识的抽象性，学生往往在做完该实验后，只是初步学会了迈克尔逊干涉仪的调整及利用迈克尔逊干涉仪测量激光波长和圆心处（最高干涉级）条纹明暗条件的方法，而对其他条纹的明暗条件不甚了解，甚至不能很好地理解条纹偏离同心圆环的原因。在实际实验中，学生较难调出满足实验测量要求的实验现象，调出的往往是椭圆形干涉条纹或弯曲的线型条纹等。如果能通过仿真模拟将抽象的光学理论形象生动地展示出来，将对学生的学习和理解大有裨益。

针对“迈克尔逊干涉仪的调整与使用”实验，文献[8—9]基于Matlab 对该实验进行了仿真。如前所述，本文将首先从理论上推导干涉条纹的光强分布公式，再基于 Mathematica 软件仿真模拟干涉条纹，并研究实验中两反射镜不严格垂直实际情况下的光强分布，并做Mathematica 仿真模拟。

迈克尔逊干涉仪示意图如图1 所示，加上扩束镜后，等效光路图如图2 所示。需要说明的是，在实际实验中扩散光源的张角很小，因此图2 中的夹角i很小。图2 所示属于等倾干涉，干涉条纹定域于无穷远。当实验者观察等倾干涉条纹时，眼睛相当于一个凸透镜，并在视网膜成像。

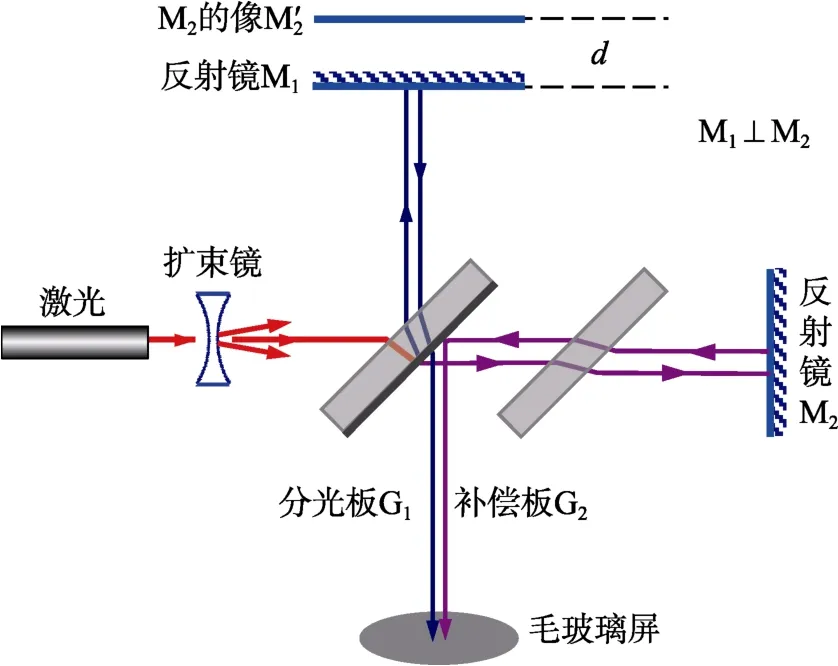
图1 迈克尔逊干涉仪实验示意图

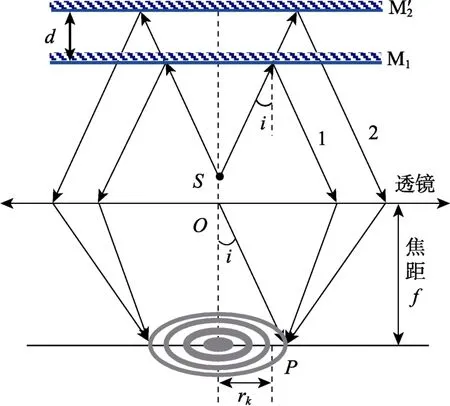
图2 等倾干涉光路示意图

入射光经固定反射镜M1和移动反射镜M2反射后到达光屏的光强为λ为波长，相应的相位差为：

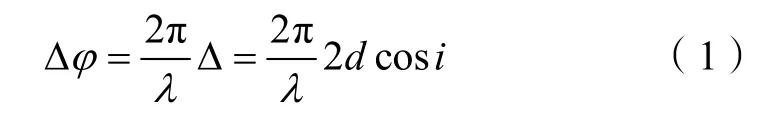
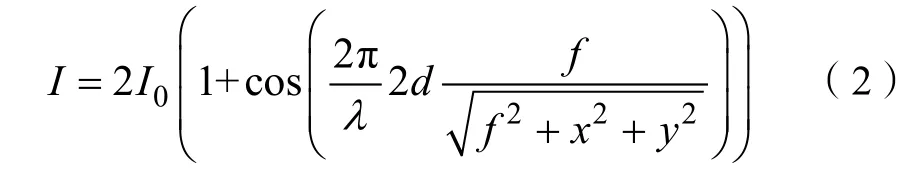
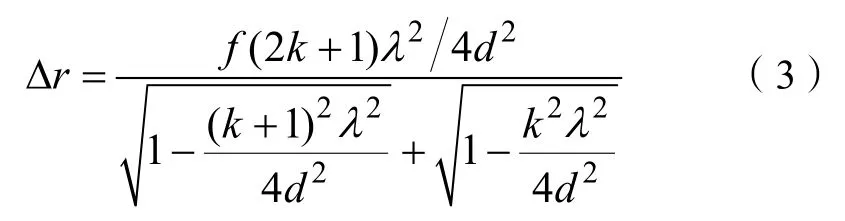
（3）式表明，两相邻的明条纹间距Δr是级次k的单调递增函数，可以看出级次k越大，间距Δr越大，级次k越小，间距Δr越小，由于里环干涉条纹级次k大，外环干涉条纹级次k小，因此，整体干涉条纹为里环稀疏，外环密集的明暗相间的同心圆环。

在实际实验中，受各种因素的影响，两反射镜M1、M2不会严格垂直，从而导致M2的虚像M2′ 与M1不严格平行，存在一个很小的夹角θ，如图3 所示。在实际实验中，由于夹角θ很小，因而可认为两条反射相干光线是平行的。

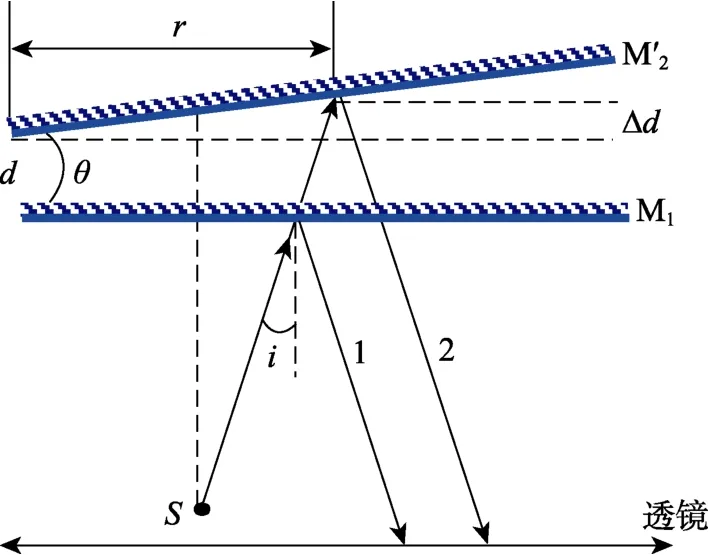
图3 M2 的虚像 M′2 与M1 不平行时的光路示意图

图3 中M2′ 向哪个方向倾斜是随机的，本文将针对沿x方向（图中水平向右）的倾斜进行讨论，沿其他方向倾斜的结果类似。在此情况下，两光束的光程差为：

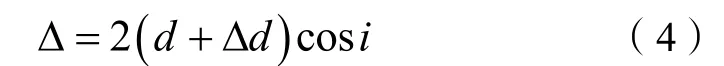
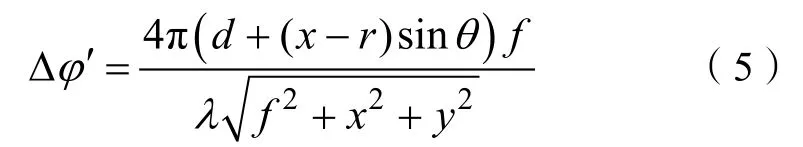
光强I可表示为：

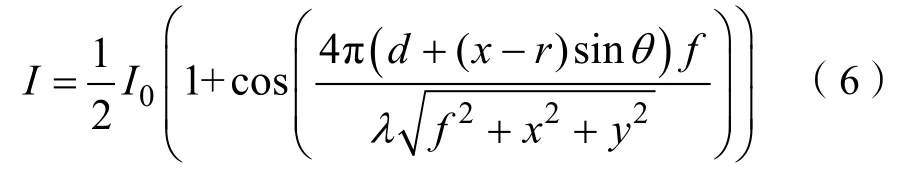
当θ=0 时，上式又回到理想情况下的式（3）。

2 干涉条纹的Mathematica 仿真模拟

在Mathematica 中有一个简单的命令Manipulate，使用这个命令就可以创造出各种丰富的交互式应用。计算Manipulate 之后输出的是一个人机互动的对象，这个输出不是一个静止结果，而是一个能交互的运行程序，它包含一个或多个控件（滑块等），使用这些控件能改变一个或多个参数的数值。它基本的输入命令是Manipulate[expr,{{u,uint},umin,umax}]，将命令输入后，便会产生一个带有控件的expr 的版本，该控件允许u值交互式操作。再利用软件中DensityPlot 函数便可以方便地画出干涉条纹，其中ColorFunction 函数中的Hue 颜色函数还可以使光波长和颜色相匹配，使仿真模拟过程更加生动形象。

利用 Mathematica 的交互功能，便可仿真模拟迈克尔逊干涉仪所产生的干涉条纹。结合光强分布式（6），在Mathematica 中输入如下语句：

便得到如图 4 所示的仿真动态演示图形。语句中的DensityPlot[f, {x,xmin,xmax},{y,ymin,ymax}, …]命令用来绘制关于x和y的函数f的密度图形，画出干涉条纹，括号里除公式外，其他命令 PlotPoints、PlotRange、ColorFunction 等的顺序可随意调换，对格式要求低。通过控件（滑块）可以调节空气膜厚度d、波长λ、焦距f、夹角θ等参数以观察不同情况下的图形，相应的交互式动态图形会同步显示出来。

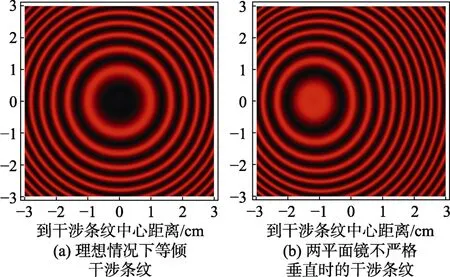
图4 迈克尔逊干涉仪的Mathematica 仿真模拟

在本文的模拟中，波长取氦-氖激光波长λ=632.8 nm，显示出红色干涉条纹；若取λ=589.3 nm（纳黄光），则显示出黄色干涉条纹。用Mathematica 软件仿真模拟出来的图形与实验中实际观察到的图形（见图5）很类似。

图5 迈克尔逊干涉仪实验观测条纹

偏离同心圆的干涉条纹是实际操作过程中常会遇到的情况，原因是反射镜 M1、M2不严格垂直，从而导致反射镜M2的像M2′ 与M1存在一个小的夹角。从图4 和图5 可以看出，Mathematica 模拟仿真动态图形与实验观测到的条纹符合很好。利用 Mathematica 软件，可以把光学实验的实验现象通过光学实验模拟仿真更直观地展现出来。

3 牛顿环干涉条纹的Mathematica 仿真模拟

牛顿环属于等厚干涉，是大学物理实验中必修的一个光学实验。牛顿环在科研和生产实践中具有重要作用，如测量平凸透镜中曲面的曲率半径，检查光学球面的加工质量等。文献[6—7]、[11—12]分别基于LabVIEW 和Matlab 进行了仿真模拟。在实际装置中，由于平凸透镜与平板玻璃接触时，接触处由于压力产生形变，致使接触的不可能是一个点，再加上玻璃上可能有灰尘存在，必然引起附加的光程差。考虑附加光程差后，牛顿环光强分布为[12]：

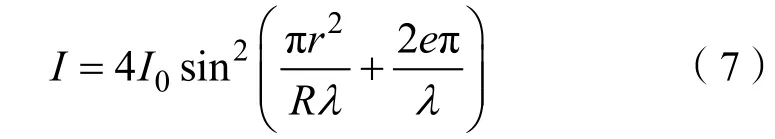
基于光强分布式（7），在Mathematica 中输入如下语句：

便得到如图6 所示的动态演示图形。

图6 牛顿环干涉条纹的Mathmatica 仿真模拟图像

图7 牛顿环实验观测条纹

图6 中曲率半径R、波长λ和附加光程差e三个参数均可通过控件中的按钮调节，从而观察不同条件下的牛顿环干涉条纹。图7 是学生实验测量过程中观测到的条纹。从图6 和图7 可以看出，Mathematica 模拟仿真动态图形与实验观测到的条纹符合很好。

4 双棱镜测钠黄光波长实验干涉条纹的Mathematica 仿真模拟

“双棱镜测钠黄光波长实验”属于双缝干涉实验，实验原理简单，但对实验操作的要求非常高。在实际操作过程中，学生很难在规定时间内完成实验，难以达到预期实验效果。目前已有很多学者从不同角度针对该实验做了大量理论研究，文献[13—15]探讨了用计算机仿真模拟双缝干涉实验问题。

在Mathematica 中同样可以通过Manipulate 命令输入相应的语句，得到如图8 所示的仿真动态演示图形。该实验原理是双缝干涉实验，在实际中双缝间距约为1～2 mm，而在实际调节过程中，狭缝宽度约为0.2 mm，由于存在单缝衍射效应[16]，双缝干涉的光强分布为：

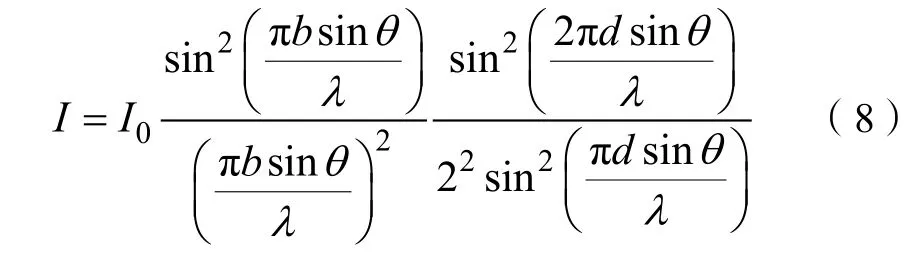
在 Mathmatica 中，由于考虑了此单缝衍射效应，因此出现图8 所示的光强减弱过程，但在实际观察中此现象不是很明显。

图8 中的各参数，如狭缝距离X，狭缝宽度b，狭缝到光屏的距离d等，均可手动调节，或者通过点击图中的►按钮使其自动变化，从而显示相应的动态图像。

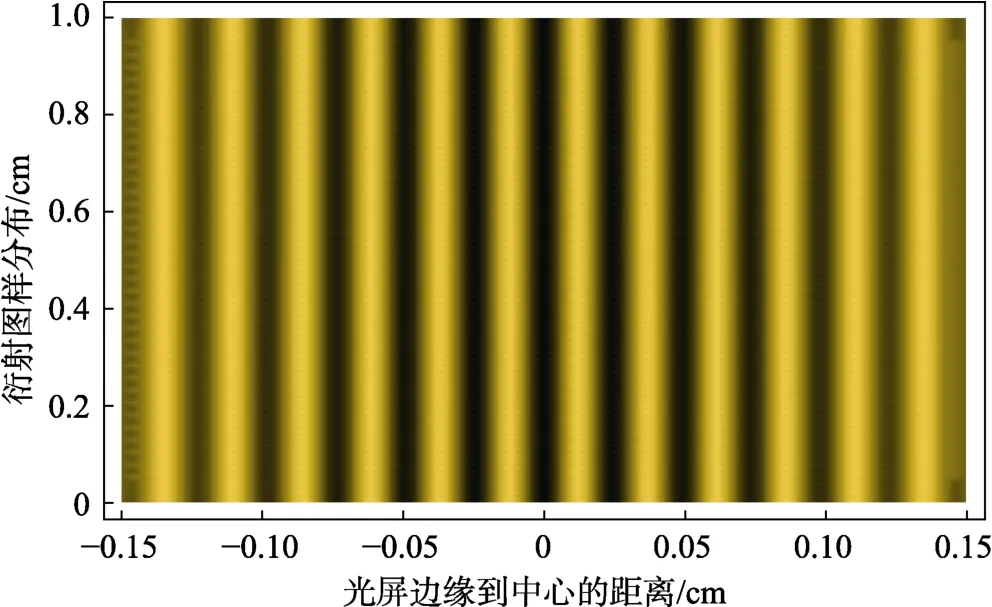
图8 “双棱镜测纳黄光波长实验”干涉条纹的Mathmatica 模拟图像

5 结语

针对大学物理实验中三个典型的光的干涉实验，本文首先从理论上给出了光强分布公式，进而通过Mathematica 软件仿真模拟，直观地把实验现象随实验参数变化的动态过程展现出来。仿真模拟程序的输出可以是cdf 格式，可直接在安装Wolfram Player 等APP的移动设备上进行操作和观察。Mathematica 软件的优势在于可以不受实验仪器和实验条件的限制，而且可以利用生成的模拟平台直接得到直观生动的实验现象，避免调节设备、无法看到实验现象、繁琐的实际操作步骤等问题的困扰。通过 Mathematica 软件仿真模拟，能够使学生由动态实验现象入手，理解该实验所涉及的物理原理，从而更快地学会对实验的调节和对实验现象的判断。此外，Mathematica 软件还可以仿真模拟牛顿环、光栅衍射、用双棱镜测量纳黄光波长等光学实验，以及其他力学和电磁学实验等。因此，笔者认为 Mathematica 软件应该走进大学物理课堂的更多实验，让学生从物理课本的平面知识中走出来，去感知更加立体的仿真模拟，从而使学生加深对物理原理的理解，提高科学素养，激发学习兴趣。