Image texture smoothing method by a novel L0-norm optimization model①

Nie Dongdong (聂栋栋), Ge Xindi②, Zhang Tianlai

(*College of Sciences, Yanshan University, Qinhuangdao 066004, P.R.China) (* *Bank of Xingtai, Xingtai 054001, P.R.China)

Abstract

Key words: texture smoothing, structure preserving, L0-norm minimization, relative total variation

0 Introduction

The key to texture smoothing[1,2]is to remove small textures while preserving the significant edges and structures in the images. Texture smoothing is used in many fields, such as image segmentation[3,4], edge detection[5,6], object recognition[7,8]and image enhancement[9-11]. Although several proposed variation models are very effective for removing image noise, they cannot distinguish image structures and textures effectively. In Ref.[12], anL0-norm minimization algorithm is proposed to restrain the number of non-zero image gradients and produce a global sparse solution, which can preserve the image significance structure and remove detail textures and noises effectively. The advantage of theL0minimization is that it can smooth texture and preserve edges better than others, such as the weighted least square (WLS)[13], and bilateral filter (BLF)[14]. Shen et al.[15]extended theL0objective function by adoptingL1-norm instead ofL2-norm in the data fidelity term and achieved some promising results. Cheng et al.[16]presented a novel approximation algorithm forL0gradient minimization in a fused coordinate descent framework. Unfortunately, since these methods highly depend on the magnitude of image gradients, and image gradients haven’t enough structure extraction ability, the methods mentioned above cannot remove high contrast texture details effectively.

Xu et al.[17]defined a new relative total variation (RTV), in which textures and main structures show completely different properties, and presented an optimization framework based on RTV regularization term for structure-texture decomposition. Since then, many scholars have made further research on RTV to improve the discrimination between textures and structures. Ref.[18] defined a modified relative total variation (mRTV) to make it more suitable inL0-norm minimization by proposing a new function. mRTV is small in texture regions and large along structure edges. Liu et al.[19]made further extension of RTV and proposed a general relative total variation (GRTV) model by expanding the norm of windowed total variation (WTV) in RTV from 0 to [0,1].

This work presents a novelL0-norm optimization model, which combines the data fidelity term, a new gradient fidelity term and a regularization term based on theL0-norm of mRTV. Due to the non-convex and non-linear property of the optimization model, it is a challenge to obtain the solution directly. Subsequently, an efficient approximate solution is also given. It can be found that the difference between textures and main structures becomes larger with the increase of the parameterαin the proposed model. The most important thing is that the results are not only sufficiently similar to the original images but also have clear edges and suppressed textures.

This paper includes 4 sections. Section 1 briefly reviews the definition of mRTV measure and theL0gradient minimization method. Section 2 presents the optimization framework with a new gradient consistency constraint and mRTV sparse constraint. Section 3 discusses the parameters of the proposed optimization model and gives some comparison experiments. The conclusion is in Section 4.

1 Related background

Here the notations used in this work are giving in Table 1.

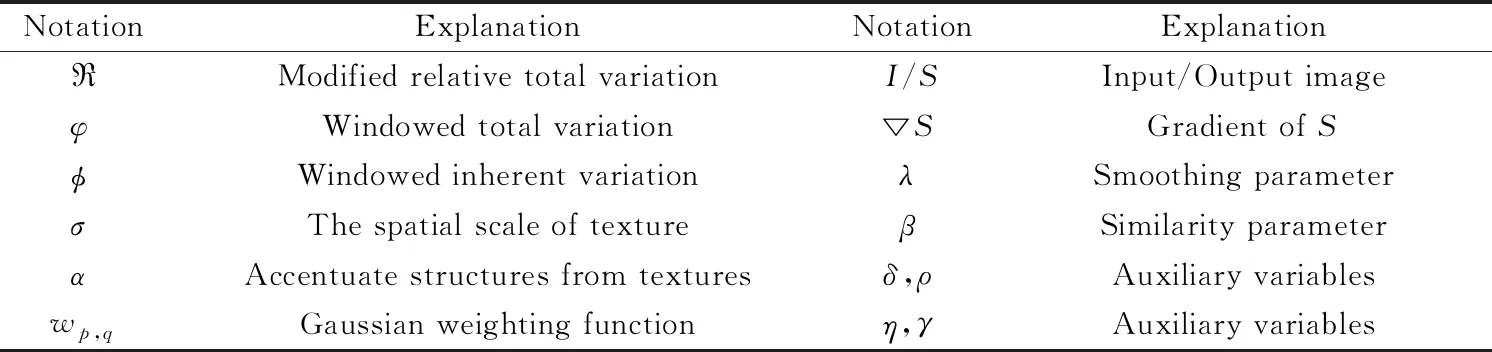
Table 1 Explanation of notations

1.1 Modified RTV measure

Based on the relative total variation, Ref. [18] proposed modified RTV measure, which is expressed as

R(p)=Rx(p)+Ry(p)

(1)

where

Rd(p)=sφd(p)φd(p)α

(2)

(3)

(4)

(5)

heresis the normalization factor,Irepresents the input image,Ωpis the set of pixels in the local neighborhood centered atppoint, and ∂dIdenote the partial derivatives ofIalong thexandydirections respectively,d∈{x,y} represents the direction to compute the partial derivatives, |·| indicates the absolute value of a number,ωp,qis a Gaussian weighting function.αis used to enhance the discrimination between structures and textures.

Compared with RTV, the modified RTV adopts an exponent parameterαto accentuate the image structures, and uses multiplication instead of division to make the mRTV values bigger along edges and smaller for textures, which makes it more suitable toL0-norm minimization.

1.2 L0 gradient minimization

L0-norm directly measures the sparsity of a vector, soL0-norm minimization is usually used to obtain a sparse solution. Many algorithms adopt it for texture details smoothing or significant edge structures extracting. However, due to the non-convexity of theL0-norm, it is difficult to be minimized directly. In Ref.[12], for the task of image texture smoothing, a split method was applied to solve theL0-norm minimization problem, which achieved good results.

Assuming thatIrepresents the input image,Sis the output image. The vector (∂xSp, ∂ySp)Tfor each pixelpis calculated as the partial derivatives ofSalong thexandydirections respectively. Then theL0-norm measures of the imageSgradients is the number of non-zero gradients, which can be defined by

C(S)=#{p||∂xSp|+|∂ySp|≠0}

(6)

According to the definition in Eq.(6), the model of image texture smoothing method based on the gradientL0-norm minimization can be written by

(7)

The data term (Sp-Ip)2is to make the output image similar to the input image. The second termλ·C(S) is a regular term, also known as a smooth term to ensure the gradient sparseness of the output image.λis a non-negative parameter controlling the significance ofC(S).

2 Proposed method

The framework of the proposed method is shown in Fig.1. Different from above 2 methods, for an input imageI, the output smoothed imageSis calculated by solving the following objective function.

(8)

where ▽ is the gradient operator, the second term is the gradient fidelity term which ensures that the gradient of the output imageSis similar to that of input imageI,λ·|R|0indicates theL0-norm of the mRTV measure of the output imageS, which directly measures the sparseness of mRTV and ensures the smoothness of the imageS.

Fig.1 Framework of this proposed method

Due to the non-convexity of theL0-norm and the non-linearity of mRTV, it is hard to solve Eq.(8) by using traditional gradient decent method directly. Inspired by the methods of Refs[12] and [18], an alternating optimization strategy is adopted to solve it iteratively.

In particular, considering the non-negativity of Rxand Ry, two non-negative auxiliary variablesδandρrespectively corresponding to Rxand Ryare introduced, then the Eq.(8) is equivalent to the following function:

(9)

The first 2 terms are the data term and the gradient fidelity term, the third term controls the smoothness of the output imageS.βis the adaptive parameter for controlling the similarity between (δ,ρ) and (Rx, Ry). The fourth term controls the sparseness of the sum of non-negative auxiliary variablesδandρ.

Define a binary function:

(10)

The Eq.(9) can be expressed as

+(Ry(p)-ρp)2)+λ·H(δp,ρp))

(11)

For the sake of simplicity, the nonlinear objective function Eq.(11) is transformed into 2 separate problems and solve it iteratively.

2.1 Solving (δ, ρ)

Fixing the output imageS, then the Eq.(11) can be represented by

(12)

Let

Bp=(Rx(p)-δp)2+(Ry(p)-ρp)2

(13)

i) Whenδp+ρp≠0 andH(δp,ρp)=1

Bp((δp,ρp)≠(0,0))

(14)

ii) Whenδp+ρp=0, that is (δp,ρp)=(0, 0), andH(δp,ρp)=0

Bp((δp,ρp)=(0, 0))

(15)

So the minimum energyBp=(Rx(p))2+(Ry(p))2is acquired when (δp,ρp)=(0, 0).

i) Whenδp+ρp≠0 andH(δp,ρp)=1

Bp((δp,ρp)≠(0, 0))=

(16)

ii) Whenδp+ρp=0 andH(δp,ρp)=0

Bp((δp,ρp)=(0, 0))

(17)

In summary, Eq.(12) has solution:

(δp,ρp)=

(18)

2.2 Solving S

Fixingδandρ, theS-estimation problem corresponds to minimizing:

+β·((Rx(p)-δp)2+(Ry(p)-ρp)2))

(19)

Due to the non-linearity of Rxand Ry, the above objective equation is still difficult to be solved. Eq.(19) is decomposed into a relatively simple problem and solve it iteratively.

In order to make the formula look more concise, letχd(p)=sφd(p)α, then Rd(p)=χd(p)φd(p).

Take Rxas an example, its non-linearity can be eliminated by approximately expanding the (Rx(p)-δp)2term in Eq.(19) as

=(χx(p)·ωp, p|∂xSp|+χx(p)

=(kxp|∂xSp|+bxp)2

(20)

(21)

(22)

(23)

(24)

Similarly, the above derivation can be also applied to eliminate the non-linearity ofRy(p).

As a result, the Eq.(19) can be transformed into the following quadratic minimization problem:

+β·((∂xSp-ηp)2+(∂ySp-γp)2))

(25)

Hereη,γonly depends on auxiliary variablesδ,ρ

(ηp,γp)=

(26)

Therefore, it can be learned that the solution of Eq.(25) converges to the solution of Eq.(19). Eq.(25) is quadratic, and thus it can be solved easily.

By diagonalizing the partial derivative operators and the accelerating fast Fourier transform (FFT), the solution of Eq.(25) in each iteration is

(27)

where

L=N·F(I)

(28)

M=F(∂x)*·F(η)+F(∂y)*·F(γ)

(29)

N=F(∂x)*·F(∂x)+F(∂y)*·F(∂y)

(30)

hereFis the FFT operator,F*denotes the conjugate ofF. The multiplication and division are all component-wise operators.

Algorithm 1 sketches the procedure of the proposed method. Fig.2 exhibits the results of different iterations. Here, it only needs 3 iterations to get a texture smoothing results. It is shown that the approximate solution given in the above deduction has a very fast convergence speed and the objective function constructed in this study is effective to texture smoothing and edge preserving.

Algorithm1: The proposed image texture smoothing method1Input: image I, gradient weight α, smoothing weight λ, detail scale σ, parameters β0,βmax2Initialization:S0←I,β←β0, i←03repeat4 Calculate Rd(p) for each pixel p in S(i)5 Solve for δp and ρp in Eq.(18)6 With δp and ρp, solve for ηp and γp in Eq.(26)7 Minimization for S(i+1) according to ηp and γp8 β←2β, σ←σ*0.92, i++9untilβ>βmax10Output: image S

3 Experiment and analysis

3.1 Discussion of parameters

There are 3 significant parameters:α,σandλin the proposed method.αis a parameter which enhances the discrimination between structure and texture,σdetermines the spatial scale of the texture features, andλis the parameter controlling the smoothness of the image.

3.1.1 Discussion of parameterα

Fig.3 shows the results with differentαvalues (forσ=3,λ=0.8). With the increase ofα, the discrimination between texture and edge structures becomes larger. In the close-up images, it can be seen that some low-contrast image structures can be better preserved. But the performance of the method on texture smoothing becomes worse with biggerα. Therefore, the parameterαin the experiments is set to [6,7] as a compromise.

3.1.2 Discussion of parameterσ

The parameterσin Eq.(5) controls the spatial weights, also determines the window size for computing the windowed variations. With the decrease ofσ(forα=6,λ=0.8), the difference of Rdbetween weak edges and textures gets smaller, which destroys the weak edge structures. Fig.4 shows that the region of skirt hem and feet becomes more blurred asσdecreases. Butσcannot be set too big, which may result in that the texture near the edges cannot be completely removed.

Fig.2 Smoothing results with different iteration

Fig.3 Effect of parameter α

Fig.4 Effect of parameter σ

3.1.3 Discussion of parameterλ

With the increase ofλ, the fidelity becomes weaker, and the structure sparsity increases, which promotes the smoothness of the result images. Fig.5 exhibits that the output image becomes smoother asλincreases (forα=6,σ=3). That is, more weak edges and textures are smoothed, and only a few main structures are preserved. But in practice, ifλis too large, the image will be over-smoothing.

Fig.5 Effect of parameter λ

3.2 Comparison with other methods

As shown in Section 2, the problem of texture smoothing and edge preserving is solved in a newL0-norm minimization model, the validity of the new objective function and the effectiveness of corresponding approximate solution are demonstrated in Fig.6 and Fig.7 by comparing the results with other 3 methods, includingL0smoothing[12], RTV[17]and mRTV[18].

The test environment is an Acer MS2360 laptop, and the software environment is MatlabR2015b. For the sake of the objectivity and fairness of the experimental results, the parameters of each method are adjusted to the best. The parameters of each method in Fig.6 areL0smoothingλ= 0.08; RTVσ=3,λ=0.015; mRTV:σ=3,λ=0.003; the methodα=7,σ=3,λ=1.3. The parameters of each method in Fig.7 are:L0smoothingλ= 0.08; RTVσ=2,λ=0.015; mRTV:σ=2,λ=0.002; the proposed methodα=3.2,σ=3,λ=0.2.

Since theL0smoothing method is heavily dependent on the magnitude of image gradients, it fails to preserve weak edges with small gradients, thus the edges on the middle pumpkin are blurred seriously in Fig.6(g). After applying RTV and mRTV to distinguish textures and edges of image, the results of the RTV and mRTV are significantly improved. And the proposed method achieves better results than mRTV by preserving sharper edges on the middle pumpkin in Fig.6(j).

Fig.6 Smoothing results and comparison on Crossstitch

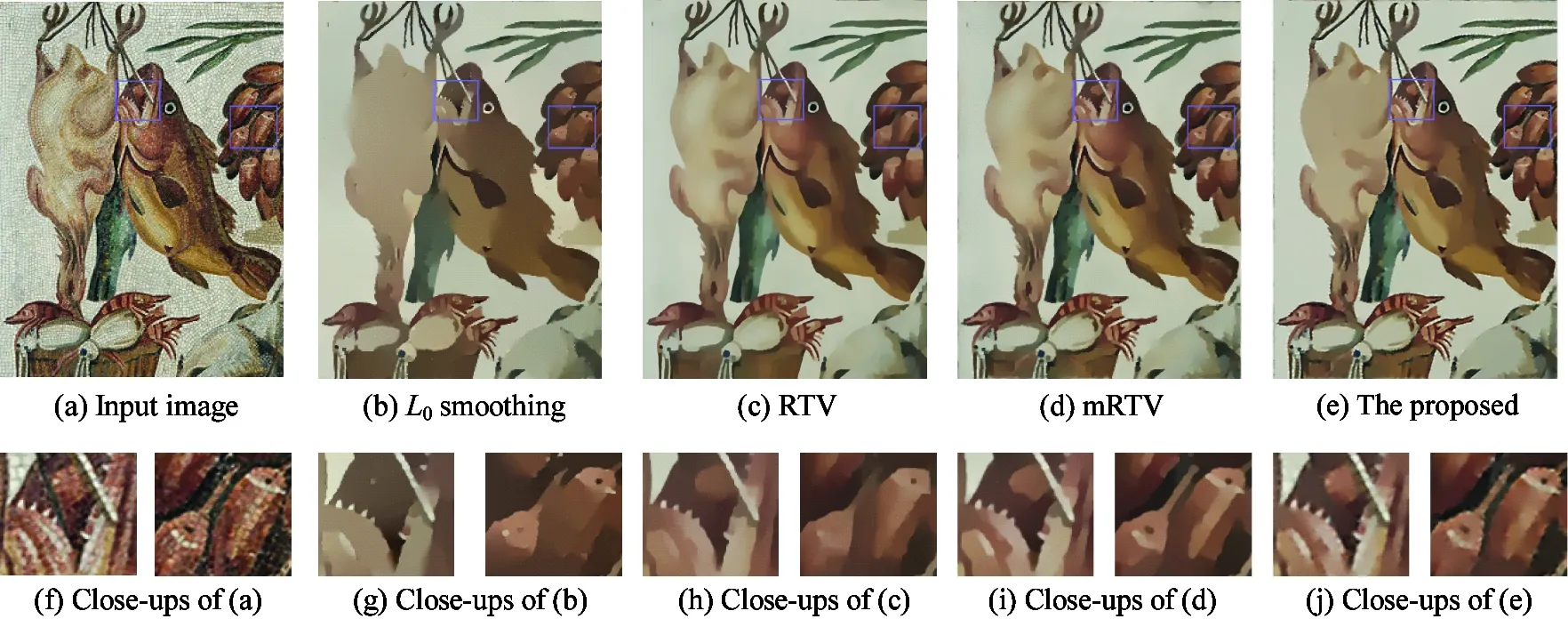
Fig.7 Smoothing results and comparison on Fish

Compared with Figs7(b), (c) and (d), the proposed method can better preserve the edges with small size or weak gradients and in the image in Fig.7(e), such as the teeth of fish and the structures on fruits.

For the sake of fairness, the edge peak signal-to-noise ratio (EPSNR) and edge structural similarity index (ESSIM)[20]are used to quantitatively illustrate the smoothing effect of the proposed method. EPSNR/ESSIM is to calculate the PSNR/SSIM value of the input image and the output image after Canny edge detection. The larger the EPSNR/ESSIM value, the better the ability of the method to maintain the structure. As can be seen from Table 2, the EPSNR , ESSIM values of the proposed method in Figs6 and 7 are higher than those of other methods.

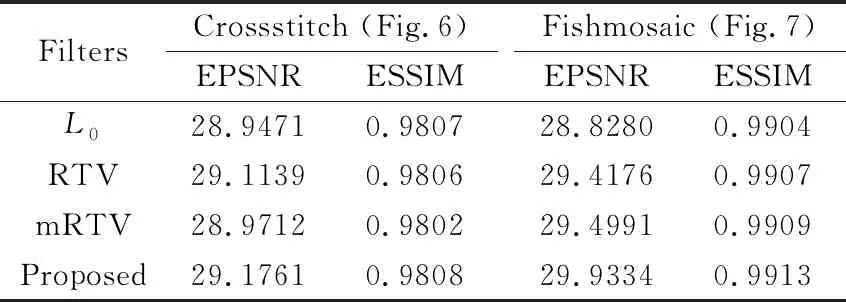
Table 2 The EPSNR/ESSIM values with different filters

4 Conclusion

A new objective function is constructed for texture smoothing and edge preserving. The success comes from 2 aspects. First, a novel optimization model is proposed to capture the structures of input images. Second, an efficient approximate solution is given by transforming the original non-linear and non-convex optimization problem to a set of subproblems that can be solved iteratively. In the future work, a variety of applications will be explored for totally applying the proposed method, such as detail enhancement, inverse halftone, and edge detection.