高速铁路半封闭声屏障声学性能的现场实测及预测模型
周 强,张 迅,郝晨曦,李 茜,李小珍,郑史雄
(西南交通大学 桥梁工程系, 四川 成都 610031)
近年来,高速铁路的快速发展给人们的出行提供了便利,但随之而来的噪声污染问题却颇受非议。传统直立式声屏障是我国高速铁路主要的噪声控制措施,高度一般为2.15~3.15 m。对于特殊敏感点,为了进一步提高降噪效果,工程人员不得不使用半封闭或全封闭声屏障[1]。
传统直立式声屏障的后方声场分布规律如图1(a)所示,即从下到上依次为声影区、低频截止区、中频截止区、高频截止区和声亮区,对应不同的声源频谱成分[2]。相关规范给出了单声源模式下直立式声屏障的降噪计算简化公式[3]。在通过多通道声阵列进行高速铁路噪声源识别的基础上,文献[4]利用双声源计算公式提高了高2.15 m直立式声屏障的预测精度。最近,胡文林等[5]进一步发展了五声源计算公式。这些计算公式实质上均是基于声衍射原理,存在较多的近似假设,但基本可满足工程应用需求。
半封闭声屏障的声传播规律如图1(b)所示。由于车体一侧封闭,高速列车噪声源在此封闭空间产生一定的混响特性。半封闭声屏障的后方声场主要由透射声构成,故噪声预测需要考虑声屏障的隔声性能。由于前述直立式声屏障的理论公式仅适用于低频率截止区到声亮区,因此,对半封闭声屏障的降噪预测需建立新的模型,但当前的研究却极为有限。
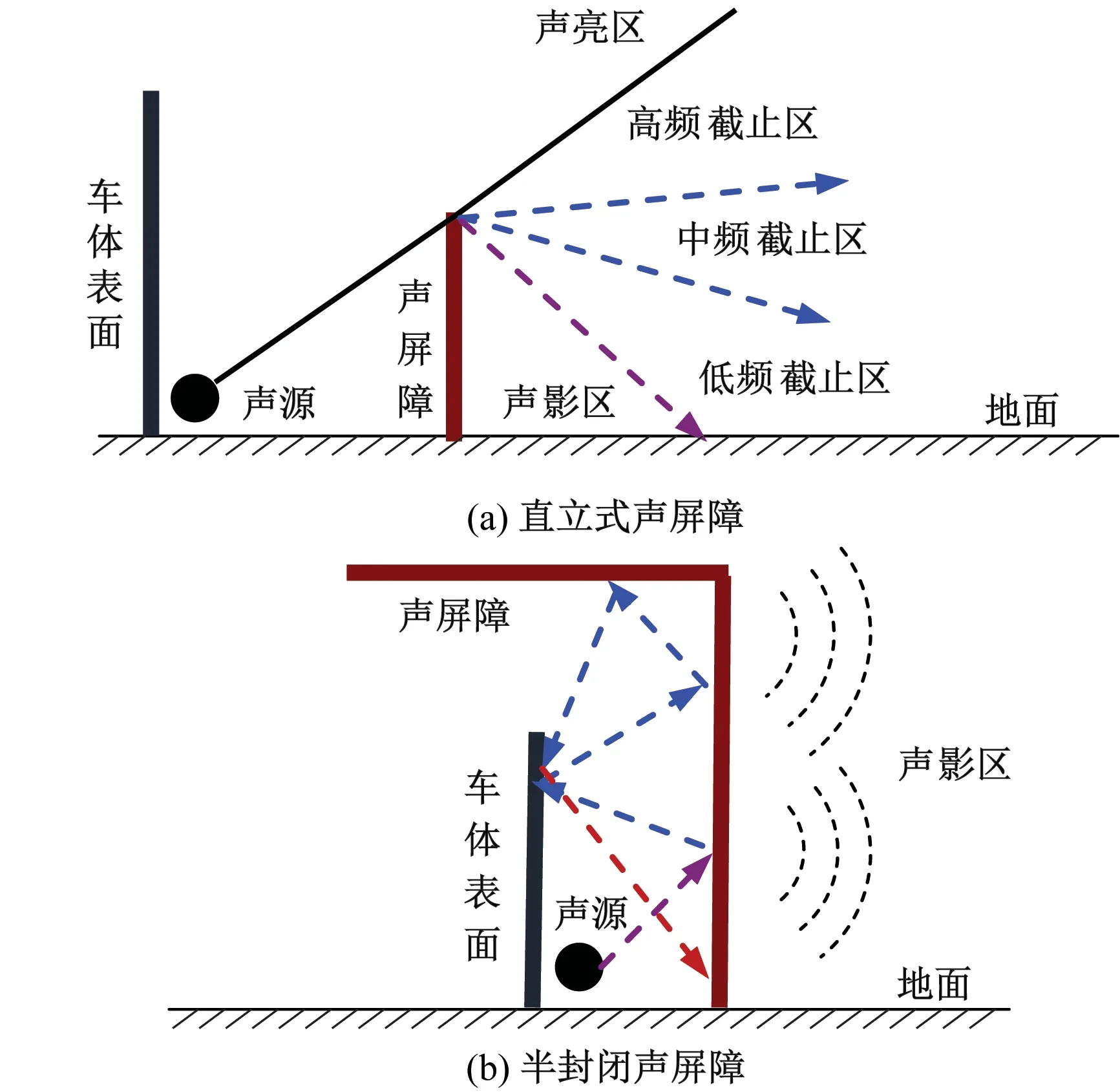
图1 声屏障降噪原理
以几何声学理论为基础的声线法在声屏障降噪性能分析方面得到了一定的应用,其最大的优势在于计算效率高,但计算精度有限[6-7]。基于波动理论的边界元法能够计算任意声学特性和形状声屏障结构的声学性能,并且可以通过优化网格质量满足精度需求。因此,近些年边界元法被大量应用于直立式声屏障的几何形状优化、声源简化、声学处理和顶部声学装置的研究中[2, 8-9]。然而,边界元方法的通常为网格数量很大的模型,需要昂贵的计算时间和存储空间,故当前多采用二维边界元法进行声屏障声学性能研究。最近,为了提高计算效率和精度,Kasess等[10]研究采用2.5维边界元法进行声屏障降噪效果预测。
统计能量分析(Statistic Energy Analysis,SEA)是一种适用于中高频振动噪声分析的方法,它运用能量的观点解决复杂系统宽带高频动力学问题[11]。文献[12]较早地引入SEA方法对直立式声屏障的插入损失进行了分析。相比于其它方法,SEA方法可以快速地建立声屏障插入损失计算模型,能够准确地描述多种噪声源特性,并能够方便地进行声屏障的结构优化设计。然而,应用SEA方法时,模型参数的正确选取和验证是关键。
考虑到半封闭声屏障结构的复杂性和边界元分析方法的缺点,本文将SEA方法引入到此类结构的声学性能分析中。首先对相关基本理论进行了简要介绍;然后,针对某高速铁路桥上半封闭声屏障开展现场测试,获取了近场声源特性、声屏障隔声量和降噪效果等参数,为预测模型的建立打下基础;最后,利用SEA方法建立半封闭声屏障声学性能预测模型,并依据现场试验数据进行模型验证。本文的研究可以实现在工程设计阶段对半封闭声屏障的声学性能进行快速评估,对降低设计成本、缩短设计周期等具有借鉴意义。
1 基本理论
1.1 能量平衡方程
SEA方法的核心思想为能量平衡,即先将结构划分为若干子系统,再对整个系统利用能量平衡方程表示能量流动关系。N个子系统的能量平衡关系为[13]
LE=ω-1Pin
(1)
式中:ω为频率;Pin为外界能量输入;E为子系统能量矩阵;L为子系统包含阻尼损耗因子和耦合损耗因子的矩阵,并且可表示为
(2)
式中:i、j和k均为子系统编号;ηji为子系统i到子系统j的耦合损耗因子;N为系统总数量。
阻尼损耗因子和耦合损耗因子是由子系统特性所决定的。耦合损耗因子遵守互易原理,即
niηij=njηji
(3)
式中:ni和nj分别为子系统i与j的模态密度。
声屏障的单元板较规则,模态密度可简化为板子系统进行计算,其模态密度计算公式为
(4)
式中:Ap为板的面积;R为截面回转半径;cl为纵波的波速。
声屏障单元板的阻尼损耗因子可以通过理论计算获得。阻尼损耗因子由三部分独立的阻尼组成,分别为材料内摩擦阻尼、声辐射阻尼和子系统边界连接阻尼[13]。常见材料的内损耗因子可从材料手册中查得,其中,有机玻璃(俗称“亚克力板”)的内损耗因子约为1×10-3,钢的内损耗因子约为3×10-4。声屏障单元板边界连接阻尼可忽略不计。声辐射阻尼在金属单元板结构中起重要作用。声辐射损耗因子为
(5)
式中:ρ0为流体密度;c为声速;σ为结构辐射比;ρs为结构表面质量。
单元板与H型钢立柱之间以直线方式连接。子系统i与子系统j以直线方式连接的耦合损耗因子可表示为
(6)
式中:τij为子系统i到子系统j直线连接的传播系数;Lij为耦合连接长度;cbi为子系统i的弯曲波速;Si为子系统i的表面积。
1.2 半无限流体
半无线流体(Semi-infinite Fluid,SIF)常用于描述声波在无边界三维空间内的声传播过程。在半无限流体内,通过声波的传播过程描述连接子系统的能量传递率,也可以将辐射声功率转化成声压等结果。
假设子系统距离半无限流体中响应点的距离为r。根据子系统的周长及面积可计算出等效宽度a和等效长度b。根据子系统和响应点之间距离的远近,可分为如下3种情况[13]:
(1)当πr≤min(a,b),即响应点距离子系统较近时,能量遵循平面波的形式进行辐射,传播截面面积为4ab/π。
(2)当πr≥max(a,b),即响应点距离子系统较远时,能量遵循球面波的形式进行辐射,传播截面面积为4πr2。
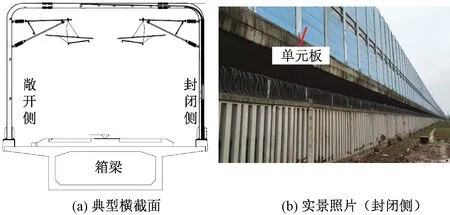
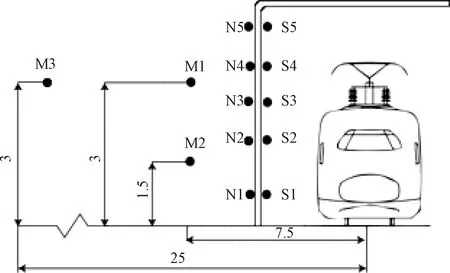
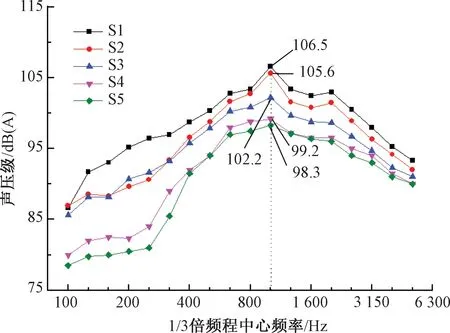
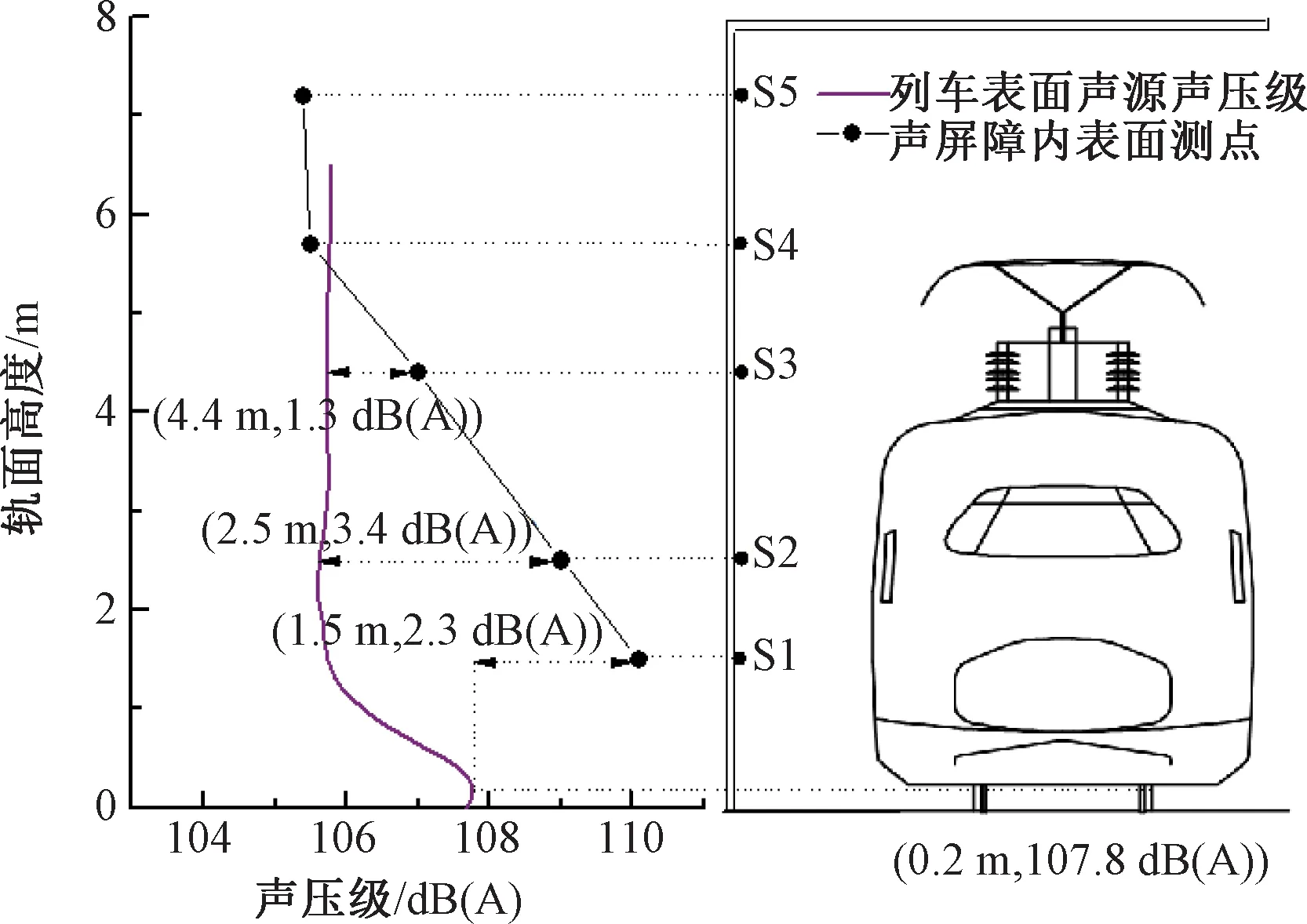
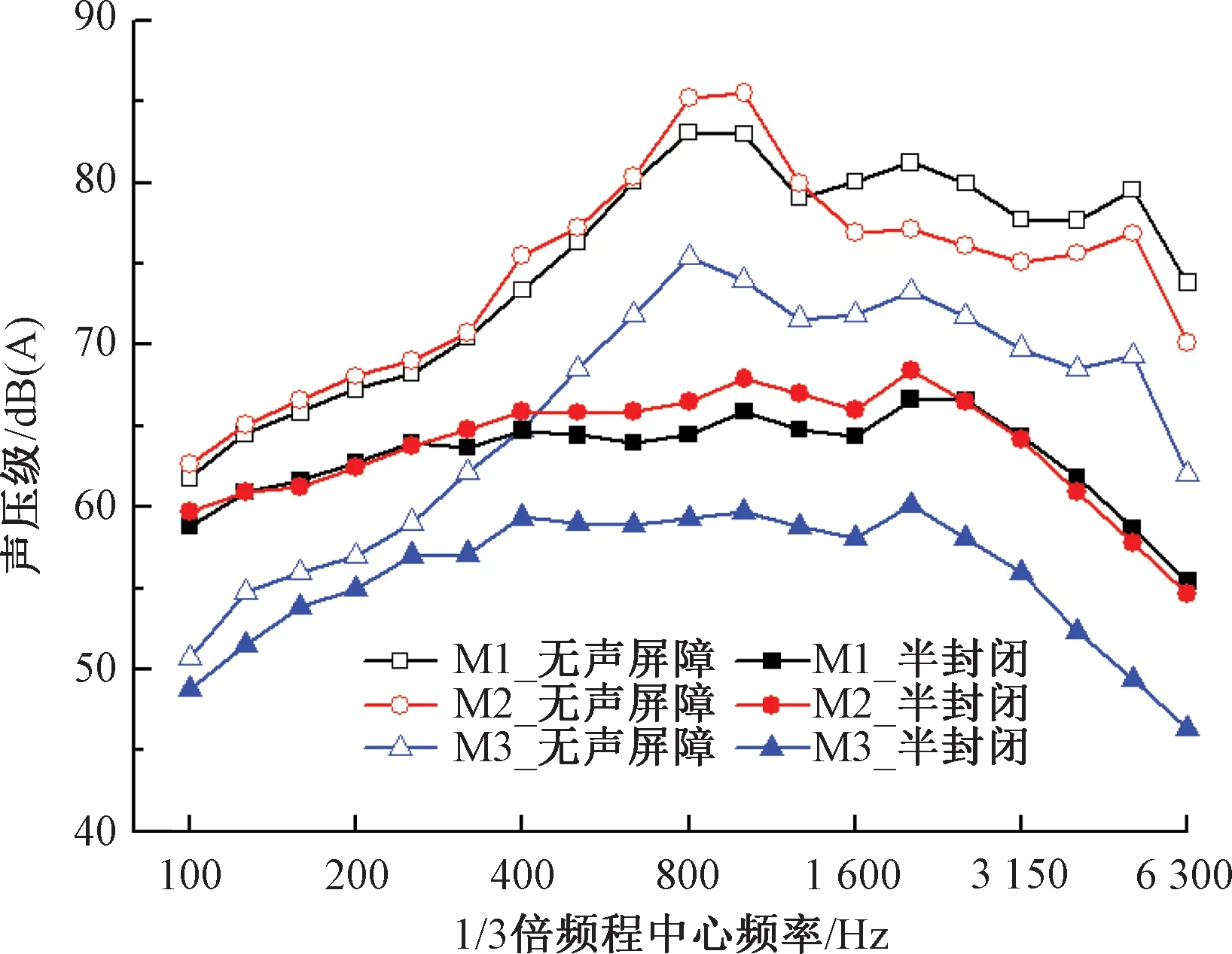
(3)当a<πr 某高速铁路通过人群密集居住区,通过设置长1.5 km的半封闭声屏障来抑制噪声的影响,见图2。该区段为多跨32 m混凝土简支箱梁组成的高架桥。轨面距地面的高度为5 m。 声屏障单元板的厚度为0.14 m,宽度约0.5 m,通过间距为2 m的声屏障立柱进行固定。桥面到声屏障高为8.15 m,由13块单元板组成,其中,第5、6块单元板之间设有1.1 m高的通透隔声板(即亚克力板),全宽11.7 m。 如图3所示,在半封闭声屏障的封闭侧布置声压传感器,其中,S1~S5位于声屏障内表面,距轨面的竖向高度分别为1.5、2.5、4.4、5.8、7.3 m;N1~N5位于声屏障外表面,与S1~S5处于同一高度。根据车体宽度,可推算得到S1~S5距列车表面的距离约为1.3 m。此外,参考ISO 3095标准,在距轨道中心线7.5 m和25 m处,分别布置测点M1~M3。由于现场测试条件限制,测点M1~M3的竖向高度相比ISO 3095标准略有调整。由于现场试验条件限制,未能在敞开侧布置对照测点。 现场测试针对过路高速列车进行,列车行经此处的速度基本一致,约为280 km/h,车型为CRH380B。试验数据处理中,先进行初步分析以剔除异常数据,再对剩余的多组有效数据进行统计分析。 文献[2]基于声源识别系统,得出高速列车车外噪声源主要分布在车间连接区域、受电弓和轮轨区域;轮轨区域噪声在各频率均为最显著声源;在整个列车高度范围内,轮轨滚动噪声对总噪声贡献率大于气动噪声。 图2 测试现场 图3 测点布置(单位:m) 声屏障内表面5个测点的声压级频谱曲线见图4。可以看出,噪声能量分布频带较广,噪声主要频率为500~2 500 Hz,与文献[2]的测试结果接近。主要噪声源来自轮轨滚动噪声,因此,从下至上的测点(S1~S5)的声压级逐渐降低。此外,各测点的频谱曲线变化规律比较相似,噪声峰值频率为1 000 Hz,且距轨面越近噪声峰值越明显。因此,以上测试数据真实可信。 图4 内表面测点的声压级频谱 由于半封闭声屏障内侧与车体表面形成相对“封闭”的空间,噪声在列车与声屏障表面之间会产生多重反射现象(见图1(b)),产生一定的混响效果并增大噪声。为了证实这一点,利用文献[2]中相同工况下测得的车体表面噪声(无声屏障)与本文测试数据进行对比,见图5。这里选取的文献[2]测试数据的测试条件与本试验在车型、车速、轨道结构和桥型等方面具有一致性。由图5可知: (1)在无声屏障时,最大声压级出现在轮轨接触面以上约0.2 m处,数值为107.8 dB(A)。随着高度增加,声压级逐渐降低,车身部位的声压级维持在105.8 dB(A)附近。 (2)在有半封闭声屏障时,S1测点的声压级相对于主要声源(轮轨以上0.2 m处)有2.3 dB(A)的增量。S2、S3测点相对于同一高度处的列车表面(无声屏障时)的噪声增加3.4、1.3 dB(A)。 (3)随着高度继续增加,声屏障内表面与列车表面(无声屏障时)的噪声接近,说明在列车高度以上的多重反射影响减弱。 图5 声屏障内表面与列车表面的噪声对比 隔声构件的入射声能与透射声能差值为隔声量。为了获得半封闭声屏障在真实服役状态下的隔声性能,以测点S1~S3及N1~N3的实测数据进行分析。根据下式可计算声屏障的隔声量为 (7) 为了比较单元板和真实服役状态下声屏障结构的隔声量,将声学实验室(以下简称室内测试)对相同单元板的测试值[15]与本试验(以下简称现场测试)的测试值进行对比,见图6。 图6 不同场合下的声屏障隔声量对比 图6表明现场测试和室内测试分别得到的隔声量频谱曲线变化规律基本一致,但在量值上前者明显小于后者,即真实服役状态下的声屏障隔声效果略差。 上述现象的产生原因可能有:一是高速列车通过时的脉动风压、轮轨振动荷载均会使得声屏障单元板发生变形,造成单元板之间存在缝隙而泄漏噪声;二是箱梁、声屏障等二次噪声的影响。考虑到二次噪声相比高速列车噪声要小得多,本文在后续建模环节将重点分析声泄漏的影响。 测点M1~M3的声压级频谱曲线见图7。为了进行对比,图7中还给出了文献[2]在无声屏障情况下(其他测试条件一致)的测试结果。由图7可知: (1)相比无声屏障情况,设置半封闭声屏障后,各测点的声压级频谱曲线相对较平坦,后者的主要噪声频段为400~3 150 Hz。 (2)设置半封闭声屏障后,测点M1的声压级小于测点M2,主要差异表现在400~2 000 Hz频段。这是由于测点M2距离列车主要声源(轮轨区域)较近,而半封闭声屏障情况下的绕射声影响很小。 (3)对比有、无半封闭声屏障的情况,低频范围的声压级差异相对较小,而中高频范围差异明显,变化规律比较一致,这是由于文献[2]与本试验的测试条件具有可比性。 依据文献[17],将图7中半封闭声屏障与无声屏障两种情况下的测试结果作差,以求得测点M1~M3的插入损失,结果见图8。由图8可知: (1)插入损失在400 Hz以下频段较小,约为3~6 dB。这是由于声屏障在低频段的隔声量较小,即声屏障对中高频噪声的控制效果较好,与直立式声屏障的插入损失规律一致。 (2)插入损失在1 250~3 150 Hz范围出现明显的波谷,这是由于声屏障隔声量在此范围出现下降所致(见图6)。 (3)半封闭声屏障在场点M3(距轨道中心25 m远)的总体插入损失(即降噪效果)为12.7 dB(A),相对于高速铁路高2.15、2.65、3.15 m直立式声屏障而言[2],分别提高5.7、3.7、2.9 dB(A)。 图7 测点M1~M3的声压级频谱 图8 测点M1~M3的插入损失频谱 在建立半封闭声屏障预测模型之前,首先建立单元板隔声模型,重点考虑单元板之间缝隙引起的声泄漏影响,并进行模型验证。 通过VA ONE软件建立的单元板隔声模型见图9。该模型包含单元板子系统和声腔子系统。其中,单元板子系统的尺寸为0.5 m×2 m,定义为铝材属性;根据单元板的实际构造,采用五参数模型添加厚80 mm的多孔吸声材料;单元板窄边与H型钢立柱的连接简化为固定约束。 图9 单元板隔声模型 为了考虑声泄漏的影响,依据矩形缝隙透声系数理论[17],计算声屏障缝隙的透声系数,再得到修正后的声屏障隔声量为 (8) 式中:s1、s2分别为缝隙和单元板的面积;τ1和τ2分别为缝隙和单元板的透声系数。 通过反复调整,在模型中添加不同宽度的矩形缝隙进行分析,结合测试结果获得的最佳缝隙模拟宽度下的预测值见图10。图10中的现场测试和室内测试曲线与图6一致。可以看出: (1)针对室内测试情况,采用0.2 mm缝隙时的隔声量预测值与测试值吻合良好。这里考虑0.2 mm缝隙是因为室内测试也不可能做到完全不漏声的绝对密封状态;另外,真实的吸声材料属性与模型存在一定的差异。 (2)针对真实服役情况,采用1.0 mm缝隙时的隔声量预测值与测试值吻合良好。 (3)对比结果显示,0.8 mm的缝隙差将造成明显的隔声量差异,高频时的隔声量差异可达10 dB左右。因此,应采取可靠的措施加强单元板连接缝隙的处理。 图10 声泄漏的影响 根据高速列车与半封闭声屏障的轮廓,利用SEA方法进行半封闭声屏障建模,如图11所示。 预测模型的纵向长度设置为80 m,这主要是考虑到声屏障降噪效果评估一般针对距轨道中心25 m远的测点,而为了获得较好的模拟精度,声源长度需大于测点到声源中心距离的3倍以上[17]。 子系统划分按照单元板的实际尺寸确定,确保模态数在分析频段内大于5,以满足SEA计算要求。同时,对单元板定义1 mm的缝隙以考虑声泄漏。内部声腔子系统的划分与单元板保持一致。整个模型的子系统共有6 560个。 图11 半封闭声屏障的SEA预测模型 文献[18]指出,将声源考虑成单极子或偶极子声源时,对声屏障插入损失的计算结果影响非常小。由2.2节可知,声屏障内部实测噪声主要来源于轮轨噪声,并包含气动噪声、弓网噪声等,此外还有少量桥面板振动噪声。因此,这里以2.2节中的实测声屏障内部噪声(S1~S5)为依据,利用SEA中固定约束的概念,忽略声源之间的干涉,定义内部声腔子系统的声压级。 最后,利用半无限流体(SIF)定义考察场点,将其与声屏障外表面进行连接,以获取半自由空间的辐射声场 测点M1、M3声压级频谱的预测值与测试值对比见图12。由图12可知,二者吻合良好,仅在个别频段存在差异,可能的原因是箱梁、声屏障等的二次噪声对测试结果造成一定的影响。就总体声压级而言,M1与M3的预测误差均小于2 dB(A),具有较好的预测精度。 进一步地,将该模型中的半封闭声屏障除去,便可获得无声屏障时的声场。将有、无半封闭声屏障的预测结果相减,可获得任意位置的插入损失。以测点M3为例,该位置处插入损失频谱的预测值与实测值对比见图13。 由图13可知预测曲线和实测曲线吻合较好,在400 Hz以前和3 150 Hz以后存在明显差异。由于测点M3的声压级频谱在400 Hz以前和2 000 Hz以后迅速衰减(图7),因此,这些差异不会对测点的降噪效果评估造成影响。相比无声屏障情况,计算得到测点M3的降噪效果为11.4 dB(A),与实测值12.7 dB(A)非常接近。 图13 测点M3插入损失频谱的预测值与测试值对比 本文以高速铁路桥上半封闭声屏障为对象,采用现场试验和SEA方法对其声学性能展开研究。主要结论如下: (1) 半封闭声屏障内侧与高速列车形成相对“封闭”的空间,噪声在列车与声屏障表面之间产生多重反射。随着高度增加,多重反射影响减弱。相比无声屏障时列车表面的噪声,半封闭声屏障内侧表面的噪声在列车高度范围内有2~3 dB(A)的增量。 (2) 真实服役状态下的桥上声屏障隔声量要小于声学实验室内的测试值,主要原因是高速列车脉动风压、轮轨振动荷载使得声屏障单元板发生变形,造成单元板之间存在缝隙而泄漏噪声。 (3) 相比2.15、2.65、3.15 m高直立式声屏障,半封闭声屏障在距轨道中心25 m位置的降噪效果分别提高5.7、3.7、2.9 dB(A)。 (4) 声泄漏会使得声屏障的隔声量下降。数值模型中考虑1.0 mm宽缝隙时,隔声量预测值与真实服役状态下的测试值吻合良好。 (5) 基于SEA方法的半封闭声屏障预测模型可以较好地模拟其在真实服役状态下的声学性能,具有较好的预测精度。 公路、城市轨道交通与高速铁路的声源分布不一致,但在确定声源后,仍可以借鉴本文的建模方法进行半封闭或全封闭声屏障的声学性能研究。本文的现场测试有限,今后还需对高速铁路半封闭/全封闭声屏障开展更多的测试工作,以进一步对其降噪性能进行深入研究。2 现场试验
2.1 试验概况
2.2 声源特性
2.3 隔声量
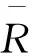
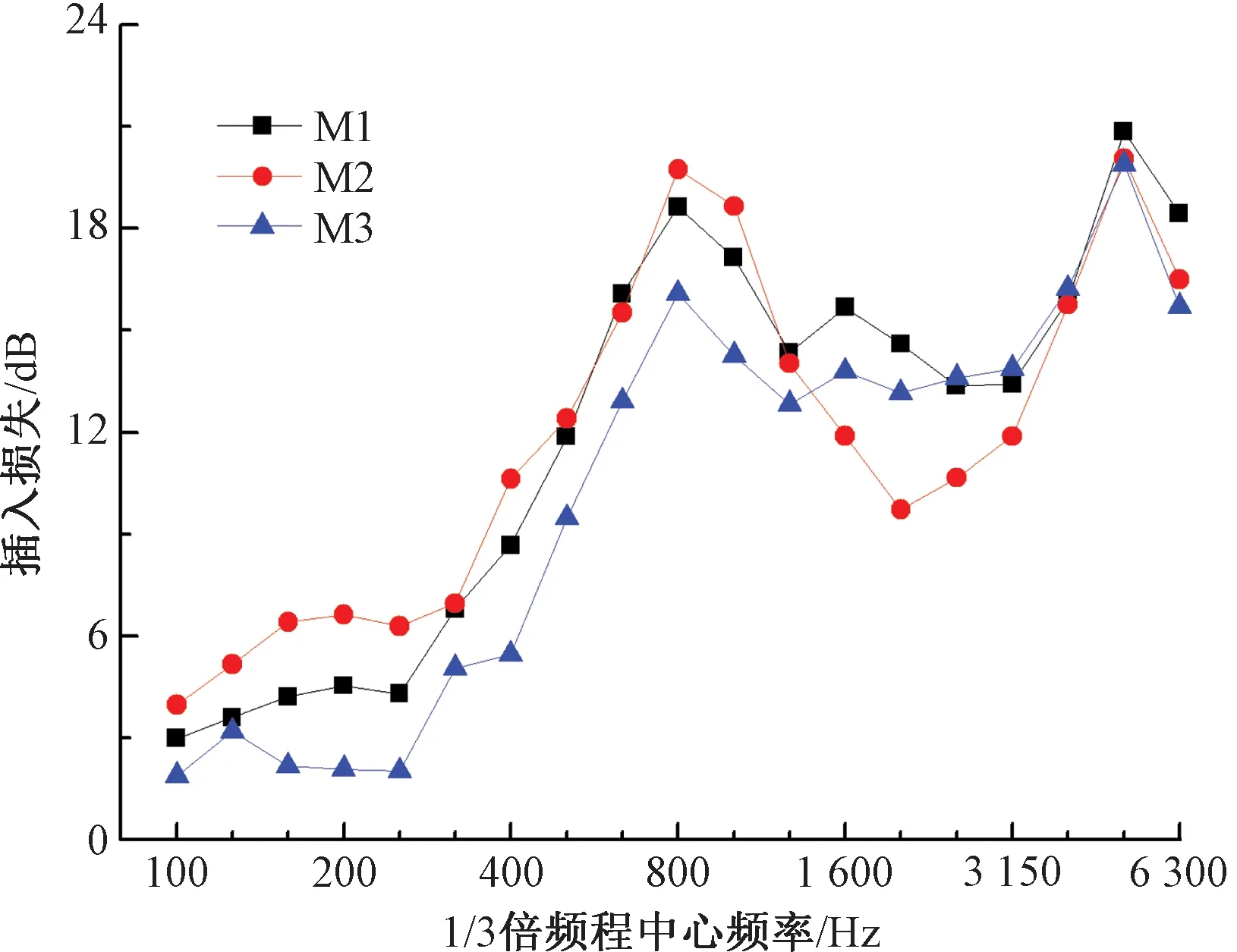
2.4 降噪效果
3 预测模型
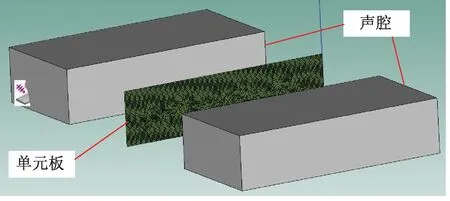
3.1 声泄漏的模拟

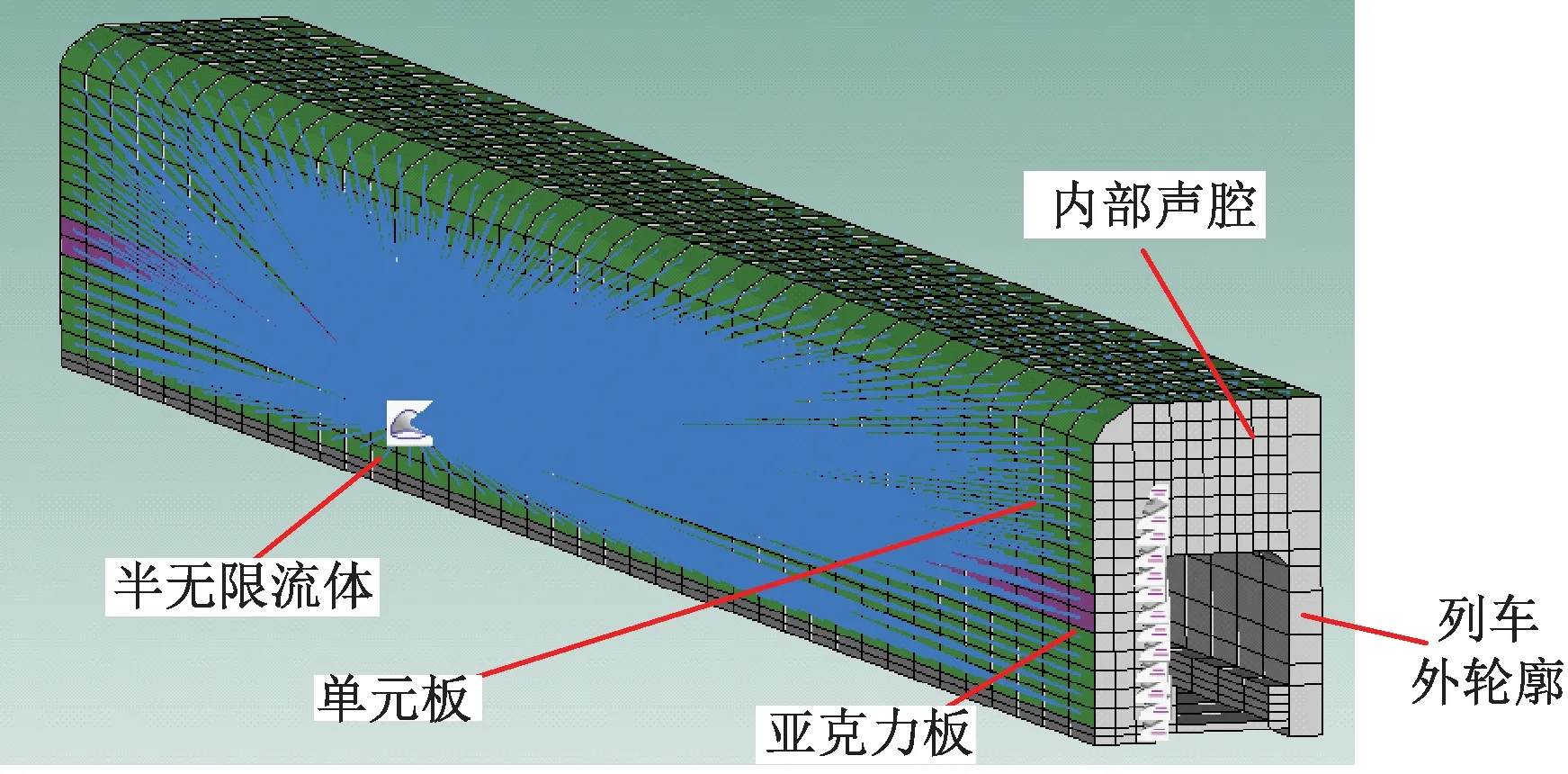
3.2 半封闭声屏障
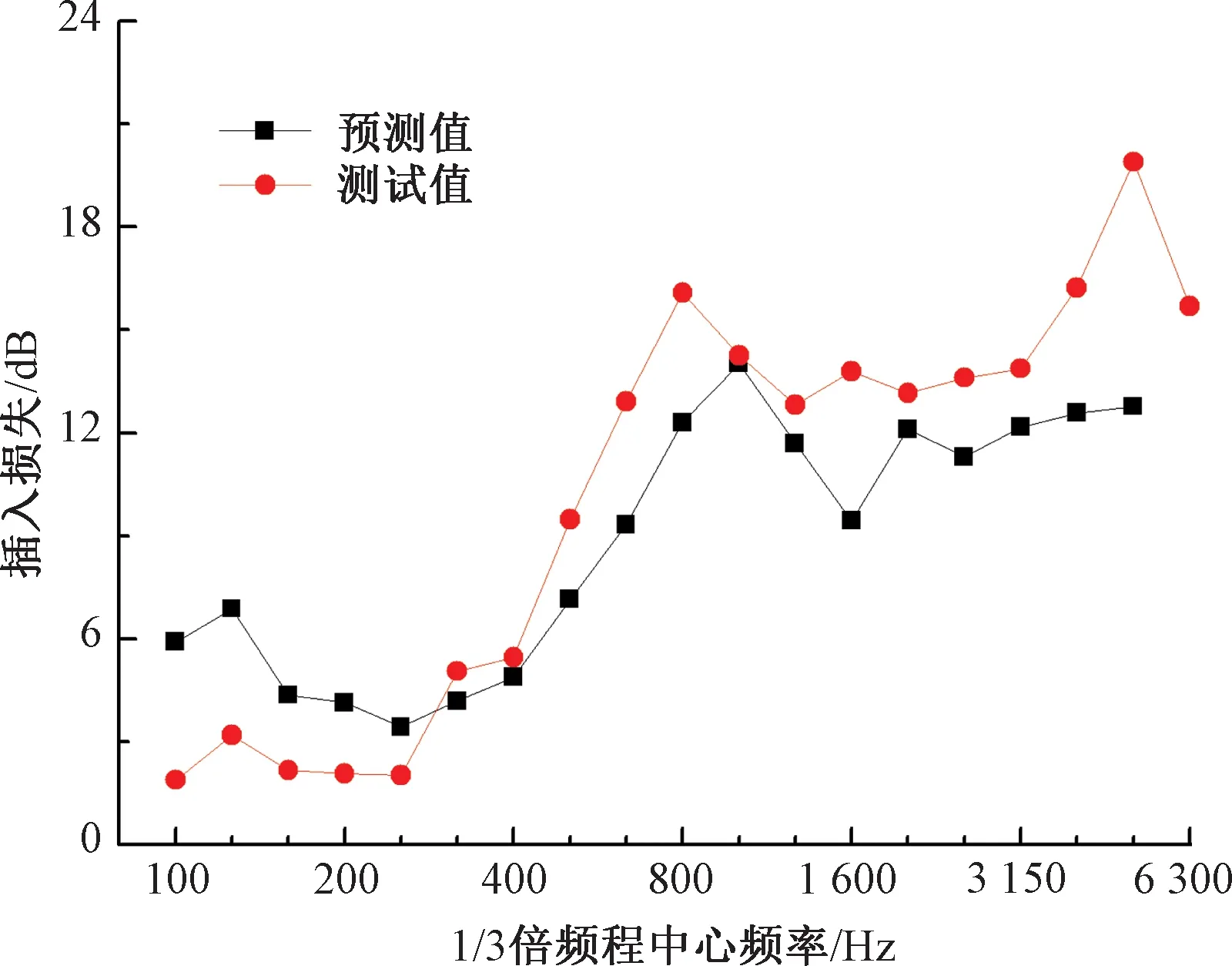
3.3 模型验证
4 结论

