和田风沙土单滴头点源入渗特征研究

包 城，秦子程，高福祥，刘 杰，洪 明

(新疆农业大学水利与土木工程学院，乌鲁木齐 830052)

0 引 言

滴灌作为当前世界上最节水的灌溉技术之一，在我国干旱及半干旱地区的农业生产中得到了广泛的应用[1,2]。滴灌属于局部灌溉，土壤湿润体的形状、大小和内部水分分布直接影响着灌溉水利用效率和作物的根系分布，开展滴灌条件下土壤入渗及其影响因素的研究，对于指导滴灌系统的正确设计和科学运行管理具有重要意义[3]。国内外学者已对滴灌条件下土壤入渗特性开展了大量研究，形成了原位入渗试验[4]、室内入渗试验[3,5,6]及数学模拟[7-11]3种较为成熟的研究方法，为后续研究的开展提供了可借鉴的经验。新疆和田地区近年来将发展设施农业作为当地群众脱贫的重要措施之一，截至2018年底各类设施农业发展面积已达1 873.14 hm2。由于新建设的大棚多位于沙漠边缘，大棚内耕作层土壤主要为风沙土。目前对常规土壤的入渗及水分运动特性研究成果较多，但有关和田风沙土在滴灌条件下水分入渗的研究却鲜有报道，由于缺乏对和田风沙土滴灌条件下水分入渗规律的研究，导致了灌溉管理粗放、水肥利用效率低、高投入低产出的问题突出，因此极有必要针对广泛分布于和田地区的风沙土开展水分入渗规律研究。本研究通过室内入渗试验，分析滴头流量、土壤初始含水率及土壤容重对滴灌单点源入渗的影响，以期为滴灌技术在该地区设施农业的推广应用提供一定的理论依据。

1 材料与方法

1.1 供试土壤

本试验于2019年2-5月在新疆农业大学农业水利工程实验室进行，试验用土取自和田市和田县经济开发区和谐新村温室大棚内，该土壤质地组成以细沙以上沙粒为主，结构松散、孔隙度大，土壤剖面的层次分化不明显[12]，平均干容重1.58 g/cm3，饱和体积含水率和田间持水率分别为37.5%和20%。土壤的颗粒组成见表1。

表1 项目区土壤机械组成Tab.1 Soil mechanical composition in the project area

1.2 试验装置

试验装置由供水装置、试验土槽和滴头3部分组成(见图1)。供水装置采用自制的可调节高度的马氏瓶和连接滴头用的乳胶管组成，采用压力补偿式滴头供水，通过乳胶管和马氏瓶连接。试验用土槽的长宽高分别为100、3和120 cm，将风沙土过2 mm筛子后装入土槽进行入渗试验。

图1 土壤入渗实验装置 Fig.1 Soil infiltration experimental setup注：1-马氏瓶；2-实验土槽；3-滴头；4-橡胶导管；5-阀门；6-马氏刻度瓶

1.3 试验方案

根据已有的研究结果[3-6]，本文的研究重点考虑了滴头流量、土壤干容重和初始含水率3个因素。调研发现，当地农户多采用滴头流量3.2 L/h的滴灌带供水，加之近年来新疆广泛推广低压小流量滴灌技术，因此滴头流量选择0.8、3.2 L/h 2个水平。在作物定植后但未灌水前，土壤结构通常较为松散，土壤容重相对较小，经过一段时间的灌溉后，沙土在重力作用下自然坐实，容重变大。因此本次试验土壤容重设置1.45、1.55 g/cm32个水平，分别模拟刚定植后和生育后期2种状态下的土壤干容重。容重1.45和1.55 g/cm3的供试土壤的饱和含水率(体积含水率)分别为35.02%和36.17%。土壤初始含水率的选择同时考虑到生产实际和试验观测效果2个方面，设置2%和4%(质量含水率)2个水平。试验采用完全随机设计，共设8个处理，各处理的具体内容见表2。每个处理设置3个重复，取平均值进行数据分析。

表2 试验设计Tab.2 Experimental design

1.4 试验方法

(1)配土。根据土壤含水率及容重的定义，先估算每次试验的实际用土重量。测定过筛后土壤的初始含水率，根据设计容重和初始含水率要求，计算需要加入的水量，然后将水和土充分搅拌均匀，装入塑料桶同时加盖塑料膜防止水分蒸发。

(2)装土。将土壤放置阴凉处10 h后，按设计的土壤容重将土壤分层装入土槽，层间打毛，事后再进行下一次填土，直至达到设计高度。

(3)滴头流量的调节。试验开始前通过调整马氏瓶的高度，测定不同高度滴头的流量，调节出满足设计要求的滴头流量后关闭马氏瓶的出水管阀门，记录马氏瓶的初始读数并将滴头固定到土槽上口的中间，准备开始试验。

(4)入渗试验。试验开始后，打开马氏瓶的出水管阀门，在设计的时间点用记号笔在土槽侧面勾绘湿润锋，同时记录马氏瓶的度数，直至试验结束。

1.5 数据分析

试验数据的初步分析采用excel 2013，绘图采用origin 9.1进行。

2 结果与分析

2.1 湿润锋运移距离随灌水时间的变化规律

量化湿润锋发展与时间的关系，可为滴灌工程设计与技术推广应用提供理论依据。由于各处理的湿润锋与入渗时间的关系类似，故仅以T3处理为代表进行分析。图2是T3处理湿润锋运移距离与滴灌时间的关系曲线。由图2可以发现，风沙土条件下水平及垂直湿润锋的运移距离与灌水时间的关系均呈现出较好的幂函数的关系，趋势基本一致，相关系数R2达到0.98以上。

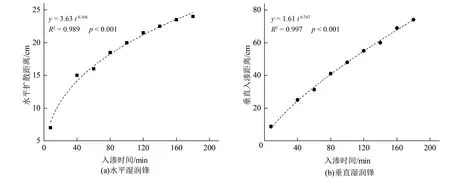
图2 湿润锋与入渗时间的关系Fig.2 Relationship between wetting front and infiltration time

已有的文献表明，幂函数曲线能较好地拟合滴灌条件下入渗时间与湿润锋发展的关系[13-16]，该函数关系可以表示如下：

y=atb

(1)

式中：y为湿润锋入渗距离；t为累计入渗时间；a，b为拟合参数。

试验各处理的湿润锋与入渗时间的函数关系的拟合参数见表3。

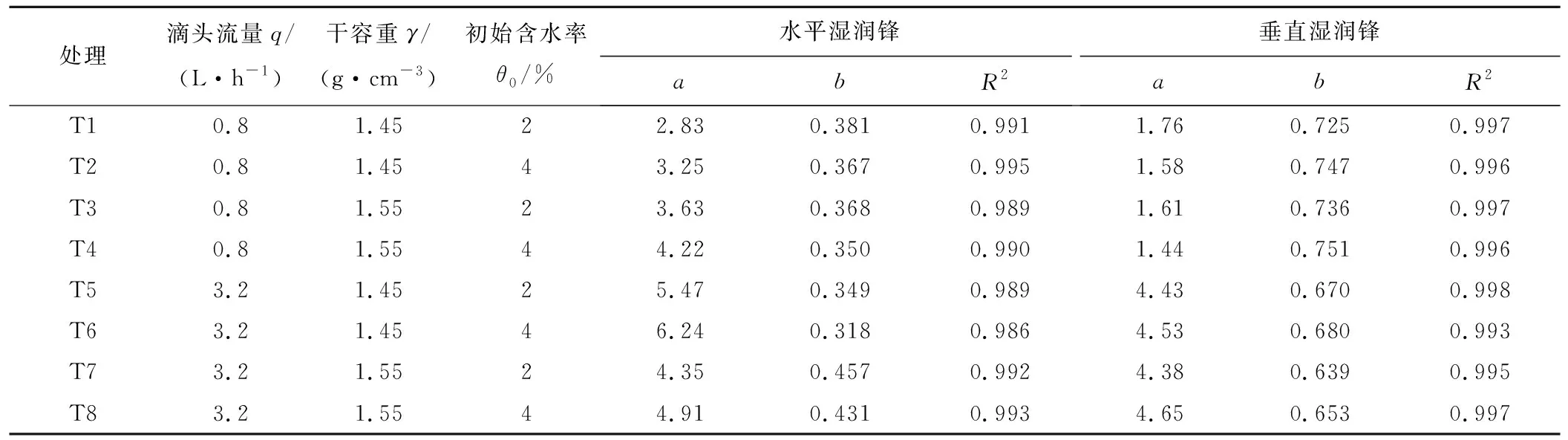
表3 不同处理下湿润锋与时间回归关系Tab.3 Relationship between moist front and time regression under different treatments

2.2 滴头流量对湿润锋的影响

图3为初始含水率2%、土壤干容重1.45 g/cm3条件下，不同滴头流量时湿润锋运移距离与时间的关系曲线。从图3可见，水平扩散距离和入渗深度均随时间增大而增大，当入渗时间相同时，滴头流量对湿润锋运移有着较为明显的影响，流量越大，水平扩散距离和入渗深度越大。分析认为，增大滴头流量相当于增加单位时间供水量，大滴头流量入渗点周围土壤含水率迅速达到饱和，水分入渗从非饱和入渗迅速过渡为饱和入渗，对于大流量滴头，往往由于滴头流量大于土壤的入渗能力，形成一定的水头，从而加大了垂直入渗距离。随着滴头流量的增大，土壤入渗能力小于供水强度，加剧了水分向水平方向扩散，从而增大水平扩散距离。

图3 不同滴头流量下风沙土湿润锋随入渗时间的变化过程Fig.3 Variation of wetting front of sandy soil with infiltration time under different drip flow

由于在进行滴灌设计时，通常依据作物种类确定计划湿润层深度，根据土壤质地确定计划湿润层深度内最大的持水能力。一旦确定了作物种类及土壤质地，一次的灌水量是相对固定的。因此，在实际生产中人们更关心灌水量一定的情况下，滴头流量对湿润锋发展有何影响[3]。图4为初始含水率2%、土壤干容重1.45 g/cm3条件下，不同滴头流量时湿润锋运移距离随入渗水量的变化曲线。从图4中可以发现，流量为0.8和3.2 L/h的滴头在等入渗水量时所对应的水平湿润锋曲线大致接近，而垂直湿润锋则随着入渗水量的增加，2者的差值呈增大趋势。结果表明，入渗水量相同时，滴头流量对水平入渗影响不大，但滴头流量对垂直入渗影响较大，且这种影响随着入渗时间的延长而加大。在实际生产中，若计划湿润层深度确定，在既定的灌水定额下，应该采用大滴头流量的滴灌带，从而减少灌溉水的深层渗漏。

图4 不同滴头流量下风沙土湿润锋随入渗水量的变化过程Fig.4 Variation of the moisture front of the sandy soil under different drip flow with the water seepage

2.3 土壤容重对湿润锋的影响

图5为初始含水率4%、滴头流0.8 L/h条件下，不同土壤干容重时湿润锋运移距离随累积入渗水量的变化曲线。从图5中可见，当入渗水量相同时，大容重土壤水平扩散距离大于小容重土壤，而垂直入渗距离则小于小容重土壤。当累计入渗水量为2.4 L时，1.45 g/cm3和1.55 g/cm3土壤容重所对应的水平与垂直入渗距离分别为 22、78 cm和26、73 cm，容重为 1.45 g/cm3的土壤水平入渗距离较容重 1.55 g/cm3的减少了 15.4%。在垂直方向上容重 1.45 g/cm3土壤的入渗深度则高出1.55 g/cm3土壤容重处理的6.8%。

图5 不同土壤容重下风沙土湿润锋随入渗水量的变化过程Fig.5 Variation of moist front of windy sand with seepage under different soil bulk density

2.4 初始含水率对湿润锋的影响

图6为滴头流量0.8 L/h、土壤干容重1.45 g/cm3条件下，不同初始含水率时湿润锋随累积入渗水量的变化曲线。从图6中可知，2种不同初始含水率的湿润锋均随入渗水量的增加而增大，且在等入渗水量时，大初始含水率的湿润锋运移距离稍高于小初始含水率。当入渗水量为2.4 L时，大、小初始含水率所对应的水平入渗距离分别为22、20.5 cm，相差1.5 cm。所对应的垂直入渗距离分别为57、59.5 cm。2者相差2.5 cm。不同初始含水率的水平和垂直入渗距离的差异并不明显，表明土壤初始含水率的变化对湿润峰的运移影响不大。

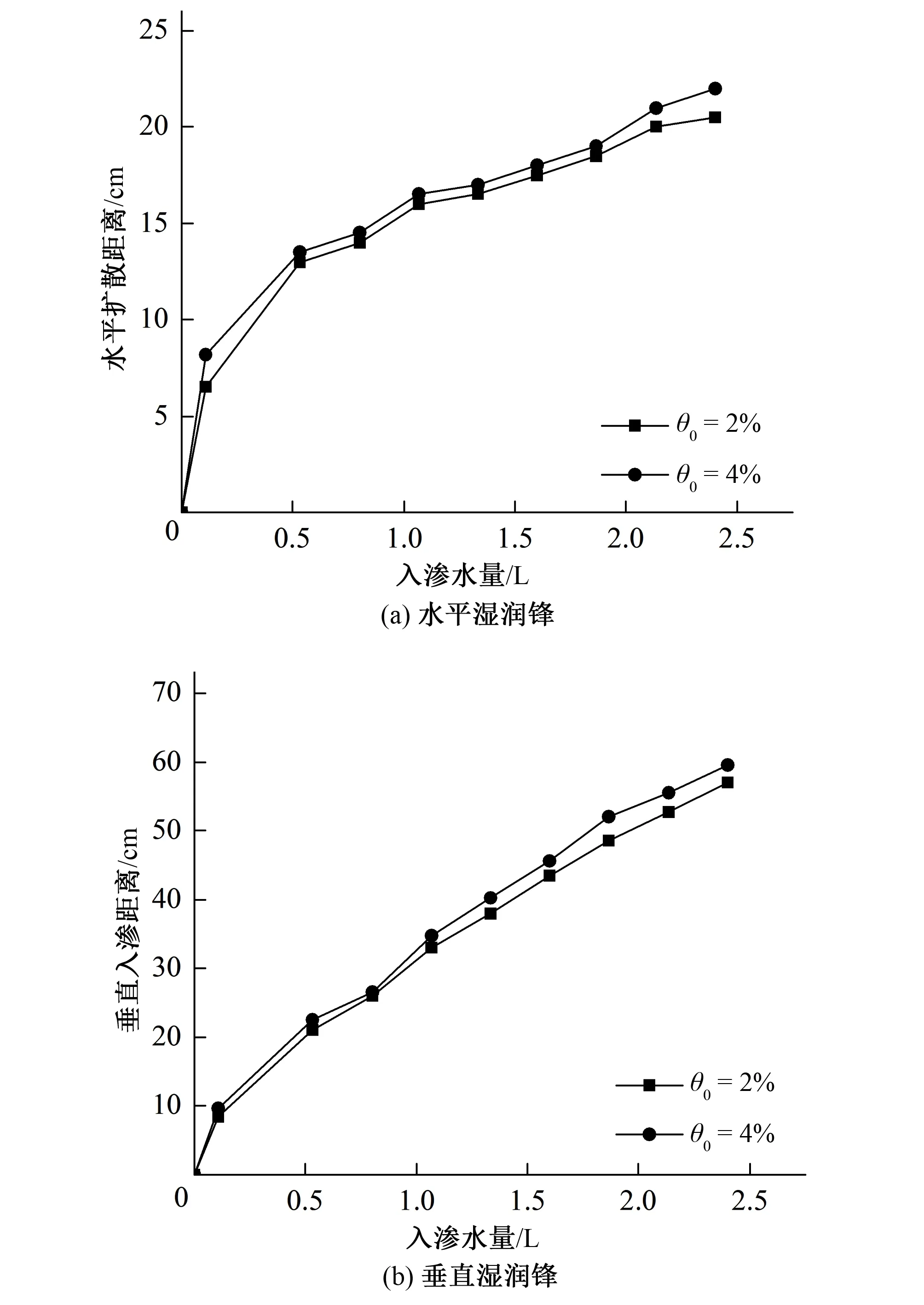
图6 不同初始含水率时湿润峰随入渗水量的变化过程Fig.6 Variation of wetting peak with seepage at different initial moisture content

3 讨 论

(1)前人研究发现当入渗水量相同时，滴头流量对水平湿润锋扩散的影响并不明显，但增大滴头流量往往会增加垂直湿润锋的入渗距离[5,13]。水平湿润锋扩散宽度与滴头流量的结论与本文结论一致。在垂直方向上，本试验结果表明在入渗水量相同时，滴头流量的大小与入渗距离呈负相关，此结论与上述前人的结论存在较大的出入。分析认为可能的原因是大的滴头流量往往超过土壤的入渗能力从而形成微小的水头，从而导致垂向入渗主要以重力势和基质势为主要推动力，照此推断在土壤质地一定，土壤基质势相对稳定，滴头流量越大，重力势也往往越大，从而入渗深度也往往越大，但如此推断往往忽略了土壤孔隙中存在气体对入渗的阻滞作用，根据李援农等人[14]的研究结论，土壤中禁锢土壤空气具有一定的减渗作用，在研究土壤的垂向入渗时除了要考虑重力及基质吸力外，还应该考虑土壤空气的阻力。大的滴头流量虽然容易形成较大的重力，但也往往容易导致土壤孔隙中的气体不能及时排出而形成较大的空气阻力，小的滴头流量虽然不易形成微小的水层，同时也减小了土壤孔隙中禁锢土壤空气的量，滴头流量和土壤空气阻力综合导致了风沙土条件下，相同入渗水量时，小滴头流量的垂直入渗深度大于大滴头流量的。

(2)本研究结果表明初始含水率对湿润峰的影响并不明显，初始含水率的增大并不能显著增大湿润峰宽度，与何小梅[9]关于沙壤土的研究结论也有一定出入。文献[9]研究结果表明土壤水分在初始含水率较大的土壤中运移速率相对较快，初始含水率对湿润峰发展有一定影响。分析认为，一方面是风沙土特殊的土壤机械组成导致了上述差异。另一方面，考虑到试验的难度，选取的初始含水率差异并不大，虽然非饱和入渗的渗透系数与初始含水率成正相关，但试验选取的较小的初始含水率所对应的渗透系数相差不大，从而导致2种初始含水率下湿润峰运移宽度差异并不明显。本研究采用了室内试验，边界条件与大田存在一定的差异，不能完全反映水分在风沙土中的入渗过程，后续还需开展原位入渗试验，进一步明晰和田风沙土入渗特性。

4 结 论

本文研究结果表明：

(1)和田风沙土在单点源入渗条件下，水平及垂直湿润锋与入渗时间均呈现较好的幂函数关系。

(2)滴头流量大小与湿润锋推进速度成正相关关系。但当入渗水量相同时，滴头流量对水平扩散距离影响不大，在垂直方向，小滴头流量的入渗深度大于大滴头流量的入渗距离。

(3)土壤容重与水平湿润峰发展正相关，与垂直湿润峰发展负相关，在入渗水量相同时，大容重土壤的水平扩散距离大于小容重的土壤, 垂直入渗距离则小于低容重土壤。

(4)初始含水率对湿润体的发展有一定的影响，但不明显。当土壤含水率较小时，可忽略土壤初始含水率对湿润锋发展的影响。