汽车轮毂轴承的疲劳寿命分析*

□ 李 伟 □ 周家恒 □ 巩成龙 □ 肖耘亚

1.湖南大学 机械与运载工程学院 长沙 410082 2.韶关学院 物理与机电工程学院 广东韶关 512005

1 分析背景

轮毂轴承是汽车的关键零部件,对汽车的安全性、舒适性、经济性等具有重要影响[1-2]。目前,国外轴承公司已进入第五代和第六代产品的开发,而我国对轮毂轴承的开发比较晚,到现在为止还处于第三代的发展水平[3]。为此,国家在鼓励重点发展的产业、产品和技术目录中,将轿车轮毂轴承列为第七位。中国轴承行业协会明确提出,要开发出使用寿命超过250 000 km的第三代轿车轮毂轴承[4]。

目前,国外研究人员已对第三代轿车轮毂轴承进行了深入研究。Nagatani等[5]分别采用拓扑优化和形状优化方法,对铆合式轮毂轴承的结构进行了优化设计。Toda等[6]通过试验研究了轴端尺寸、铆装压力和轮毂硬度等对卡紧力的影响。Kajihara[7]结合有限元仿真与试验测试,研究了轮毂轴承的刚度和铆装接触面压力分布情况。Choi Donghoon[8]研究了工作游隙对轮毂轴承寿命的影响。国内研究人员在轮毂轴承结构方面进行了一定研究,如Wu Jia等[9]分析了轮毂轴承的受力情况。此外,国内也有研究人员通过有限元方法仿真分析了轴承工作时的载荷状态[10-11],汪浔[12]、卢小辉[13]对轮毂轴承的强度、刚度等进行了研究。当然,国内研究人员还未完全掌握核心的铆合装配工艺技术,导致产品尺寸离散度大,产品内在质量不稳定,使用寿命在30 000 km～300 000 km区间内不等。可见,需要开展轿车轮毂轴承疲劳寿命研究,为提升产品性能提供技术支持。

笔者以第三代轿车轮毂轴承为研究对象,建立实际运行工况下的理论力学模型和疲劳寿命计算模型,设计相应的载荷谱,并借助有限元软件建立仿真分析模型,计算应力应变场。最后借助疲劳寿命分析软件计算轮毂轴承疲劳寿命,并与实际运行情况进行对比。分析结果不仅可以为轿车轮毂轴承单元研究提供较好的理论支持,而且可以为工程人员提升产品性能提供有益参考。

2 轮毂轴承结构

第三代轿车轮毂轴承将外圈、内圈、滚动体、保持架等组件装配在一个单元中[14-15],传统的装配方式采用螺母卡紧。近年来,随着对节能、可靠性和成本等要求的日益提高,在轿车轮毂轴承的装配方式上出现了以轴端铆合式取代螺母卡紧式的趋势。铆合式轿车轮毂轴承如图1所示。NSK于2001年开发出了轴端铆合式轮毂轴承,此后KOYO、SKF等制造企业也相继成功推出了该类型轮毂轴承。这种装配方式的优点如下:① 去除螺母,减小了质量和尺寸,结构更加紧凑;② 铆合装配过程中可以对轴向卡紧力实时精确控制,从而保证装配后获得最佳预紧量,大幅延长使用寿命,提高可靠性;③ 消除了螺纹防松结构中存在的卸载隐患,显著提高了产品的安全性。国内公司生产的轴端铆合式轮毂轴承单元产品使用寿命离散度大,使用寿命较短,现有研究较少涉及使用寿命方面,未建立起明确、实用的轮毂轴承单元疲劳寿命分析方法。为此,笔者结合理论分析和有限元仿真,研究轮毂轴承单元的疲劳寿命,为轮毂轴承结构优化及铆合装配工艺改进提供理论支持,同时为轮毂轴承建立起实用的可供参考的疲劳寿命分析方法。

▲图1 铆合式轿车轮毂轴承

3 轮毂轴承受力分析

轿车轮毂轴承所承受的载荷通过轮胎轮毂施加到轴承上,轮胎所受载荷可分为径向载荷Fz和轴向载荷Fy。当轿车转弯时,受斜坡影响,外侧轮胎中心高于内侧轮胎,轮胎受力如图2所示。图2中,H为轿车质心高度,Ti为同轴两轮胎的轮距,m为满载情况下的轴载质量,β为路面坡道角,ag为轿车转弯过程中的侧向加速度,与路面平行。正常行驶中的路面坡角很小,sinβ≈β,cosβ≈1。以图示A点为力矩点,根据力矩平衡原理,可得出:

∑MA=0

(1)

式中:MA为作用于A点的力矩。

由此可得出轮毂轴承所受外载荷的计算模型为:

(2)

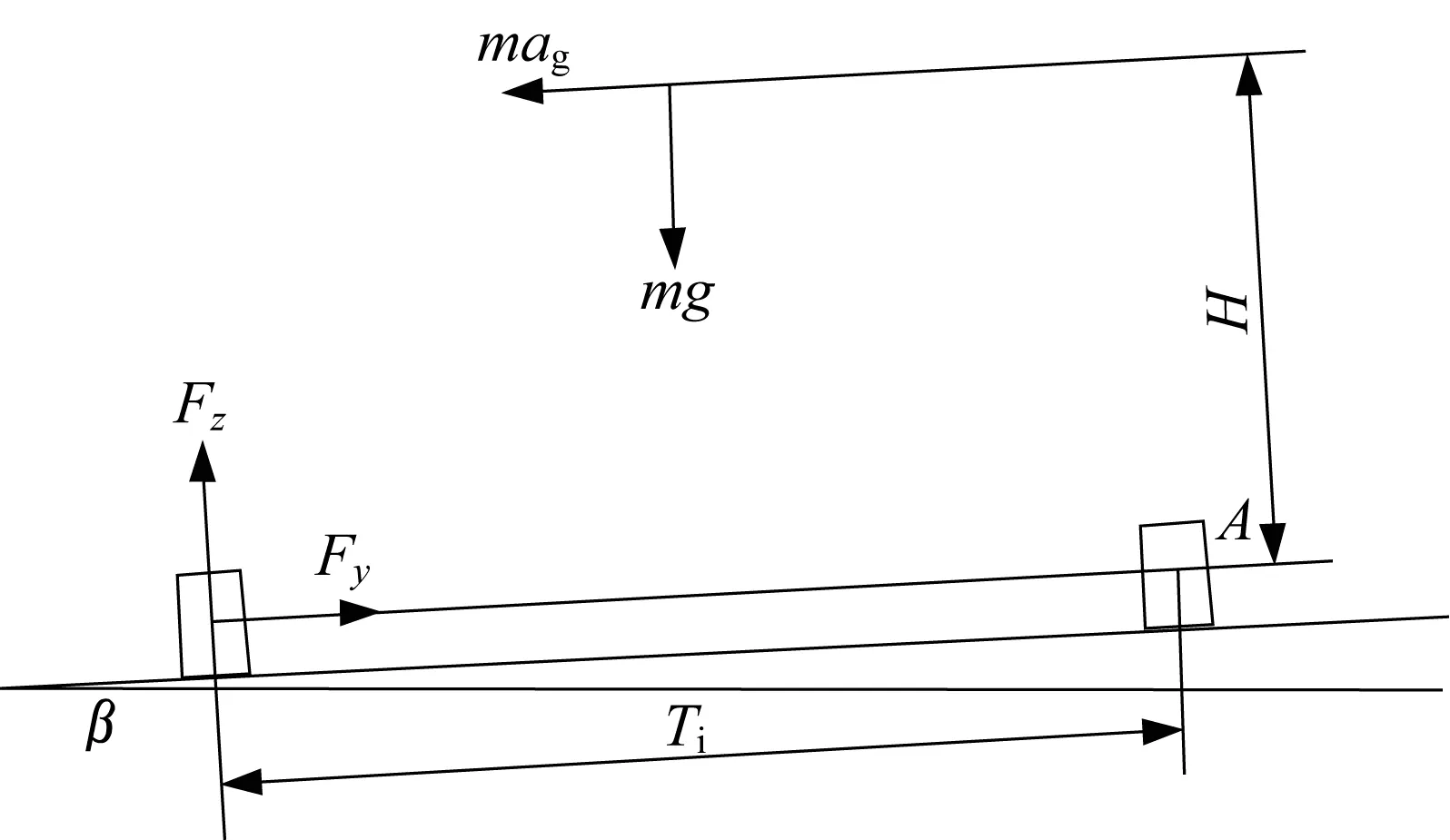
▲图2 轿车转弯时轮胎受力

笔者以某款轿车为例计算轮毂轴承受力情况,为疲劳寿命分析提供具体参数。某款轿车的具体参数见表1,根据式(2)可得到不同工况下轮毂轴承单元的受力情况,见表2。

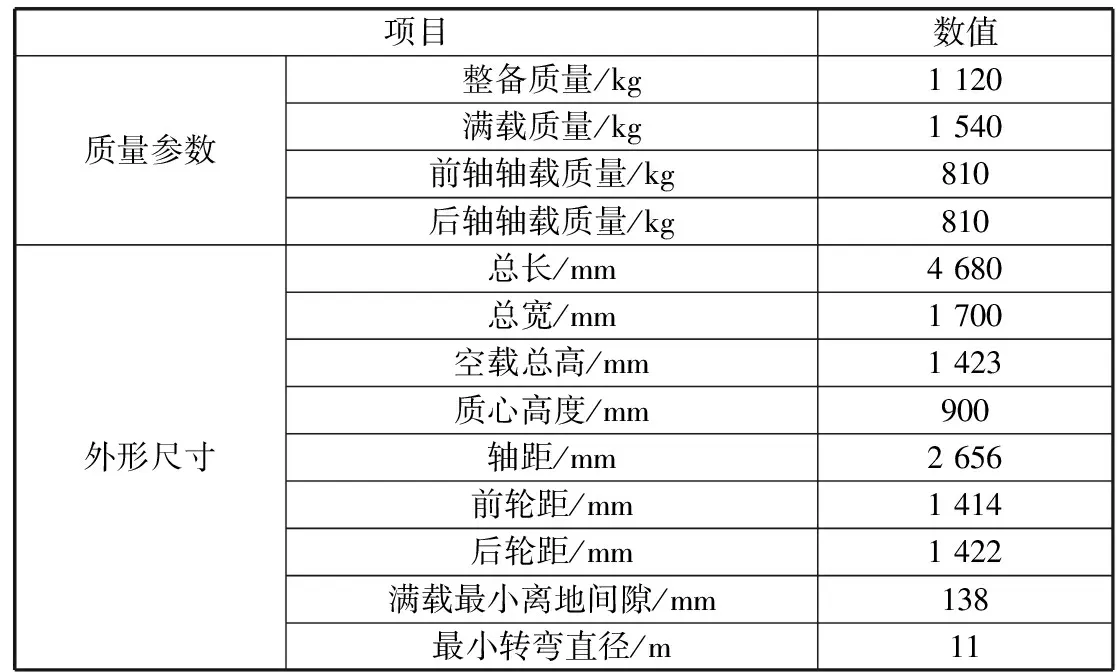
表1 轿车参数

表2 轮毂轴承受力情况

4 轮毂轴承疲劳分析

滚动轴承的疲劳寿命常采用Lundberg-Palmgren理论模型来估算[16],所研究的轿车轮毂轴承单元为两列滚动轴承单元的集成,因此也可基于该模型进行分析。通常采用的Lundberg-Palmgren修正模型为:

Lna=a1a2a3(C/P)ε

(3)

式中:Lna为轴承寿命,以转数形式来表示;a1为可靠度因数,可靠度不同,对应的a1数值也不同,当可靠度为90%时,a1=1;a2为材料因数;a3为润滑因数;C为轴承额定动载荷;P为当量动载荷;ε为指数,针对不同类型轴承,取值不同,球轴承ε=3,滚子轴承ε=10/3。

当计算轿车轮毂轴承在理想工作状态下的额定寿命时,a2=a3=1,可靠度因数为90%,a1=1。

轴承额定动载荷C常用轴承的径向基本额定动载荷Cr来表示,其理论计算模型为:

(4)

fc=Dwcosa/Dpw

(5)

式中:bm为常用高质量淬硬轴承钢和良好加工方法的额定因数,所研究轮毂轴承属于角接触球轴承,bm=1.3;fc为与几何形状、制造精度、材料等有关的因数;Dw为滚珠直径;Dpw为滚珠节圆直径;i为轴承中滚动体的列数,对于轿车轮毂轴承,i=2;a为轴承公称接触角;z为一列轴承中滚动体的总数。

Lundberg和Palmgren提出将联合载荷换算为当量动载荷。所谓联合载荷,指轮毂轴承在工作中同时受到的径向和轴向载荷。对于轿车轮毂轴承,其当量动载荷P为:

P=XFz+YFy

(6)

式中:X和Y为径向、轴向载荷因数。

当轴承公称接触角为35°时,X、Y取值见表3,表3中e为韦布尔分布斜率。

表3 径向和轴向载荷因数取值

由于径向、轴向载荷属于交变载荷,因此求得的当量动载荷为一组值。根据寿命计算模型,当量动载荷应是和额定动载荷相对应的具体数值,因此需要求出平均当量动载荷Pm来计算轮毂轴承的疲劳寿命。当轿车轮毂轴承在载荷P1、P2、…、Pi作用时,对应的主轴转速为n1、n2、…、nj,各载荷状态相应的作用时间为t1、t2、…、tk,则平均当量动载荷Pm为:

(7)

(8)

式中:v为轿车行驶速度;RS为轮胎半径。

轿车在不同行驶状态下对应不同的载荷,各行驶状态在总的行驶周期中占有一定的比例。假设一个行驶周期的时长为T,各行驶状态占的比率为q1、q2、…、qk,各行驶状态所用的时间t1=Tq1、t2=Tq2、…、tk=Tqk,因此平均当量动载荷Pm为:

(9)

实际驾驶中,轿车的行驶速度会随行驶状态和路况而改变。根据相关资料及国家对各行驶状况的比率表,当轿车在较好路面直行时,速度取100 km/h;在较差路面直行时,速度取60 km/h;处于左转和右转时,速度取40 km/h。

当在一个支持位置存在多列轴承时,整个轴承单元的寿命Lna与单列轴承的寿命Lna1、Lna2、…、Lnai之间存在如下关系:

(10)

由于本研究中轮毂轴承为双列球轴承,因此i为2,e为10/9。

根据以上分析,轿车轮毂轴承的疲劳寿命Lna为:

(11)

轿车轮毂轴承的公称接触角为35°,单列滚珠共16个,滚珠直径为11.64 mm,滚珠节圆直径为62.5 mm,轮胎半径为295 mm。该轮毂轴承为双列角接触球轴承,额定动载荷相同,即C1等于C2。总的基本额定动载荷为每列额定动载荷的2(1-1/ω),其中ω取10/3。由此可求得C1和C2为36 031 N,Cr为58 371 N。为求得轮毂轴承的当量动载荷,需先获得不同行驶状态下轮毂轴承的载荷。结合表2所求得的载荷,根据式(9)可得出轮毂轴承的当量动载荷为4 489 N。然后根据式(10)、式(11)可求得轮毂轴承的疲劳寿命约为2.77×108r。需要说明的是,理论模型并未考虑轴承的过盈装配、局部应力集中等情形,因此所求出的值为理论目标疲劳寿命,即设计目标值。轮毂轴承的理论目标疲劳寿命长于250 000 km,满足设计要求。

5 应力仿真分析

轮毂轴承结构复杂,笔者采用Unigraphics NX 12.0建模软件建立其三维实体模型,如图3所示。为精简计算过程,提高计算效率和准确度,建立的有限元模型可省去一些冗余零件,并简化结构。根据实际使用及试验情况,轿车轮毂轴承单元的内轴是关键部件,因此,重点对内轴应力情况进行分析。经过简化后的三维模型导入ANSYS Workbench软件进行分析。采用四面体网格划分实体模型,对于重要部位,如内轴根部与法兰接合部,通过Refinement模块进一步细化网格,以此提高计算精度。对内轴远离被铆轴端的一侧施加固定约束,被铆轴端一侧施加相应的载荷。轮毂轴承有限元模型如图4所示。

▲图3 轮毂轴承三维模型

▲图4 轮毂轴承有限元模型

5.1 转弯时应力情况

根据式(2)可求得轮毂轴承径向载荷Fz为5 990.0 N,轴向载荷Fy为2 396.1 N。轮毂偏移量较小,径向载荷可认为作用在两列滚道中间位置。车辆转弯时还会产生相应的力矩,轮胎半径为295 mm,轮毂偏移量为2 mm,于是可得径向载荷产生的力矩为11 980.0 N·mm,轴向载荷产生力矩为706 849.5 N·mm。输入相关受力载荷边界条件,通过有限元模型可求得车辆转弯时轮毂轴承的应力分布,如图5所示。由图5可知,最大应力产生在内轴根部与法兰接合部,为259.94 MPa。尽管该应力值未超过材料的屈服强度,但是在高周疲劳状态下,突然的冲击,如遇到沟坑等可能造成该处断裂。

5.2 直行时应力情况

直行时侧向加速度为零,因此轴向载荷Fy为零。径向载荷Fz为3 969.0 N,相应力矩为7 938.0 N·mm。输入该外部载荷,根据所建立的有限元模型可求得车辆直行时轮毂轴承的应力分布,如图6所示。由图6可知,在直行情况下,产生最大应力的位置并不是在内轴根部与法兰接合部,而是在两个内圈相接触的位置,出现这一情况可能与外载荷加载在该部位有关。由于最大应力仅为147.08 MPa,因此此处首先出现疲劳破坏的可能性微乎其微。

▲图5 车辆转弯时轮毂轴承应力分布

▲图6 车辆直行时轮毂轴承应力分布

5.3 过盈装配时应力情况

为了获得较长的疲劳寿命,在轴承装配中往往采取轴向过盈装配以形成预紧。为了研究过盈装配对轴承应力的影响,设置被铆轴端底面和与其接触的内圈端面之间的偏移量为0.3 mm,此时轮毂轴承应力分布如图7所示。

由图7可知,最大应力出现在被铆轴端底面。这是由于铆合装配过程中铆头从轮毂轴上端向下碾压轴端,使轴端逐渐变形,并在变形的末端位置产生最大应力。此处最大应力仅为12 MPa,几乎不会出现疲劳破坏现象。

▲图7 过盈装配时轮毂轴承应力分布

6 疲劳寿命仿真分析

6.1 载荷谱设计

车辆正常行驶过程中,会遇到阻力、转弯、停车、路面条件及其它各类情况的影响,这些因素都会影响轮毂轴承单元的载荷。假设轿车在平路面匀速行驶,其所受空气阻力和滚动阻力处于力系平衡中。路面条件影响引入冲击载荷因数fw来衡量[9,12],对于较差路面,fw为1.3,对于较好路面,fw为1,可据此修正轮毂轴承的载荷情况。根据相关资料统计,较能反映车辆实际行驶状况的是直行占90%、转弯占10%。为此,设计行驶状况为良好路面直线行驶占46%,较差路面直线行驶占46%,转弯占8%。此外,考虑到直线和转弯行驶状态的切换一般会有短暂缓冲,在一种行驶状态结束后加2 s的过渡时间,即直行44 s,缓冲2 s,转弯2 s,缓冲2 s。为了对比分析不同行驶状态组合下轮毂轴承的疲劳寿命,设计较好路面直行、右转、较差路面直行、左转和右转、左转、较好路面直行、较差路面直行两组行驶状态。

在直行过程中,侧向加速度ag为零,较好路面径向载荷Fz=fwmg/2=3 969.0 N,较差路面径向载荷Fz=fwmg/2=5 159.7 N。在转弯过程中,侧向加速度从零逐渐增大到0.55g,径向和轴向载荷逐渐增大。在进行左转弯时,径向载荷Fz=0.5mg+magH/Ti=6 747.9 N,对应的轴向载荷Fy=Fzag/g=3 711.32 N,此时的力矩为1 108 335.1 N·mm。在进行右转弯时,径向载荷Fz=0.5mg-magH/Ti=1 190.1 N,对应的轴向载荷Fy=Fzag/g=654.6 N,此时的力矩为195 480.5 N·mm。

根据以上分析,在MATLAB软件中建立数据文件,并保存为.csv格式文件,然后导入Ncode软件,设置相应的时间序列和通道数等,建立两组载荷谱,如图8、图9所示。

▲图8 较好路面直行、右转、较差路面直行、左转载荷谱

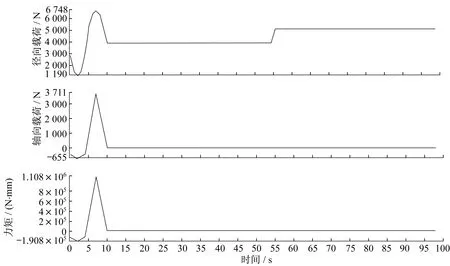
▲图9 右转、左转、较好路面直行、较差路面直行载荷谱

6.2 分析结果

为了计算轮毂轴承单元疲劳寿命,需要利用所建立的有限元模型求解单位力和单位力矩下的应力分布,求解中设置不同的载荷步区分力和力矩载荷。然后施加所设计的载荷谱,通过设置载荷映射求解轮毂轴承在载荷谱下的应力累计损伤,从而获得使用寿命。单位力和单位力矩作用下轮毂轴承应力分布如图10所示,最大应力位于内轴根部与法兰接合部。

Ncode软件已与ANSYS Workbench软件集成,因此只需将上述求解的仿真数据传输到应力寿命时间序列模块中,并在Ncode主界面导入载荷谱文件,设置其它相关参数进行计算,即可求得轮毂轴承的累计损伤结果与疲劳寿命结果,如图11所示。加载两种不同的载荷谱,其结果相差很小。应力云图中显示的疲劳寿命结果是基于一个周期的交变载荷,以轿车轮毂轴承单元开始运行受载到最终失效为止的循环次数来表示的,循环次数数值为1.504×104,对应的行驶里程近4万km。根据制造公司反馈的数据,所生产的轿车轮毂轴承可靠性寿命为5万km～8万km。实际使用中,轮毂轴承一般是间断性使用,且需保养和润滑,这些情况在仿真条件下还难以兼顾。考虑到这些因素,仿真结果具有较高的参考价值。另一方面,由理论模型计算得到的寿命较仿真结果大,这是因为理论模型并未考虑轴承的过盈装配、应力集中等情形。

▲图10 单位力和单位力矩作用下轮毂轴承应力分布

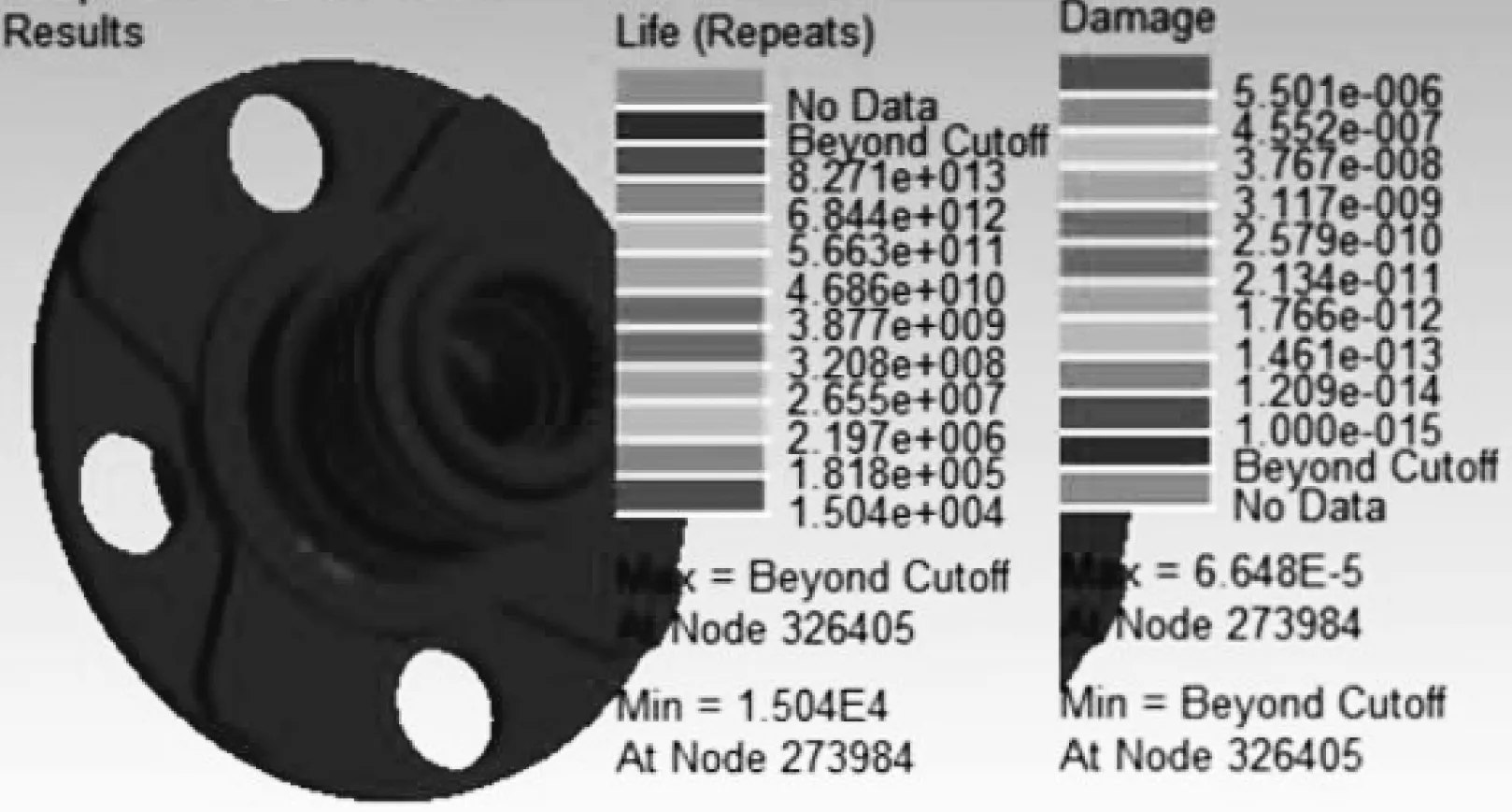
▲图11 Ncode计算结果

7 结束语

笔者建立了轿车轮毂轴承单元实际运行中所受载荷和疲劳寿命的理论分析模型,计算得到不同工况下载荷的大小和轮毂轴承的疲劳寿命,理论目标疲劳寿命约为2.77×108r,满足设计要求。

同时建立了轿车轮毂轴承单元的有限元仿真模型,根据轴承所受载荷情况仿真得到转弯时最大应力产生于内轴根部与法兰接合部,为259.94 MPa。

分析了轿车轮毂轴承的载荷谱情况,仿真得到疲劳寿命所对应的行驶里程近4万km,接近实际行驶里程。分析结果具有较好的参考价值。