双轴联动进给系统多目标优化设计与研究
苏 芳,罗茹楠,刘艳明,王晨升,
(1.山西大同大学机电工程学院,山西大同037003;2.天津大学机械工程学院,天津300350)
高精度和高效率是机床加工的两大目标。高精度、高速五轴联动加工中心是我国国防工业制造领域的重要装备[1-2]。机床的加工精度是被加工件加工质量的保障[3]。当前,表征机床加工精度的指标有定位精度、重复定位精度、轮廓误差、跟踪误差及动态误差等[4-5]。
在高速工况下,提高数控机床加工精度的方法主要有2类。一类是从机床机械结构出发,通过轻量化、结构优化等改善机械结构的静/动态特性,以使它具备更高的动态精度[6-7]。当前,对于机床的研究,大多以进给系统为突破口,通过提高各进给系统的精度及速度,来有效地提高多轴联动机床的性能指标[8-9]。如:文献[10-11]介绍了针对进给系统的动态特性影响因素及影响规律的研究;文献[12-13]针对滚珠丝杠进给系统开展了系统跟踪误差研究,并基于此开展了多轴联动精度研究。另一类是从伺服控制系统出发,结合机械结构开展伺服控制系统优化及控制系统与机械结构的匹配优化,使机床在一定的控制手段下实现高精度的运动,从而提高其精度。在对机床进行广泛研究的基础上,通过各种优化方法获得结构变量和控制变量的最优解,最终实现提高加工精度的目标。多目标优化是广泛采用的优化方法之一[14-17]。该方法是针对系统多个变量,结合各类算法,在样本空间内寻找最优解,以此来指导机床结构参数设计和伺服控制参数设置。文献[18]提出了一种柔性滚珠丝杠进给传动的最优非并列控制策略,可使滚珠丝杆进给传动具有较佳的动态特性,且降低了传感器的成本。
为实现图1所示双轴联动进给系统的优化,笔者基于多目标优化方法开展工作。双轴联动进给系统多目标优化的流程如图2所示,包括初始条件设置、试验设计、试验样本点提取、仿真分析、响应面模型构建、拟合精度检验和目标函数优化等。
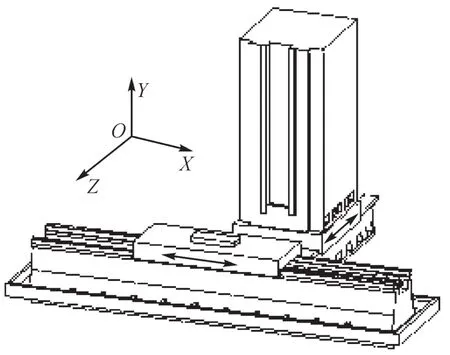
图1 双轴联动进给系统Fig.1 Biaxial linkage feed system

图2 双轴联动进给系统多目标优化的流程Fig.2 Multi-objective optimization process of biaxial linkage feed system
本文的优化研究是在前期工作的基础上开展的,双轴联动进给系统机电耦合动力学模型的精度已得到验证[5,8]。首先,选择机械系统和控制系统的参数为设计变量;其次,根据已选定的设计变量,利用Box-Benhnken方法,提取设计空间范围内的试验样本点,进而开展样本点仿真分析,获取对应的轮廓误差和跟踪误差的响应值;再次,借助二次多项式拟合方法,对已获得的试验样本点和试验样本点响应值进行拟合,构建响应面模型,并对响应面模型进行精度检验;然后,利用多目标优化遗传算法NSGA-II(nondominated sorting genetic algorithm-II,非支配排序遗传算法II),将设计目标作为优化目标,获取该目标下的Pareto最优解集;最后,在Pareto最优解集中,根据优化目标的优先原则,选择最佳参数,并根据仿真结果,输出优化结果。
1 初始条件设置及试验设计
1.1 初始条件设置
就多轴联动数控机床而言,有效地控制各进给轴的跟踪误差及耦合特性是正向抑制轮廓误差的方法之一,故选取双轴联动进给系统的轮廓误差和单轴跟踪误差为设计目标。选取双轴联动进给系统的轮廓误差为第1目标函数;由机床机械结构的特点可知,Z轴的惯量明显大于X轴,故选择Z轴的跟踪误差为第2目标函数;X轴的跟踪误差为第3目标函数。
结合前期的研究结果,选择的设计变量及其取值范围如表1所示。

表1 设计变量及其取值范围Table 1 Design variables and their range of values
多目标优化的目标函数为:
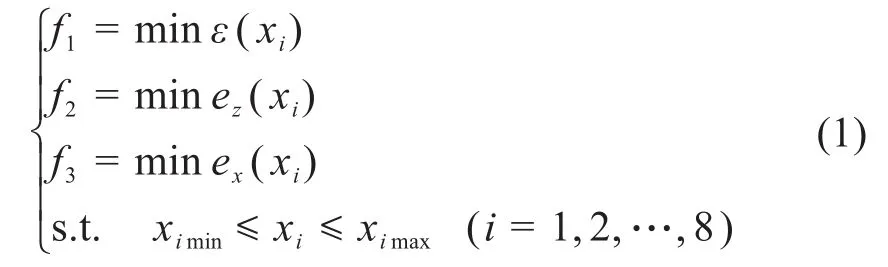
式中:ε(x)——双轴联动进给系统的轮廓误差;
ez(xi)——Z轴跟踪误差;
ex(xi)——X轴跟踪误差;
xi——设计变量;
ximin——设计变量的取值下限;
ximax——设计变量的取值上限。
1.2 试验样本点提取
根据选择的设计变量,利用Box-Behnken方法提取试验样本点,提取结果见表2。

表2 试验样本点Table 2 Test sample points
基于所搭建的双轴联动进给系统机电耦合动力学模型[5],在样本空间内进行样本点仿真,分别计算系统轮廓误差及单轴跟踪误差,结果见表3。
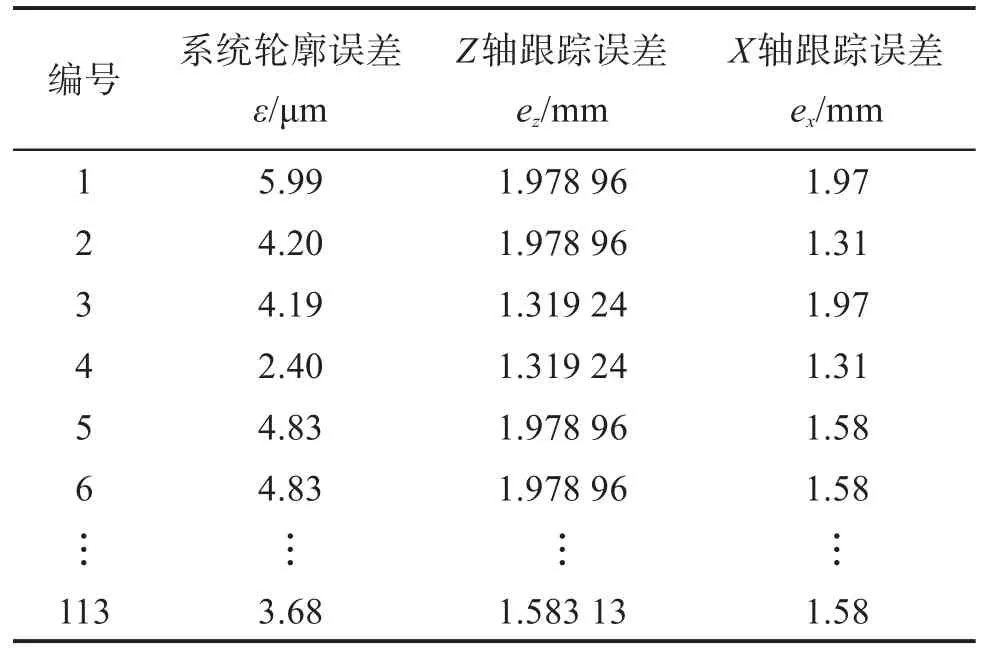
表3 双轴联动进给系统轮廓误差和单轴跟踪误差的仿真结果Table 3 Simulation result of contour error and uniaxial tracking error in biaxial linkage feed system
1.3 试验结果分析
基于设计目标,对各设计变量进行灵敏度分析,以考察各变量对设计目标的敏感性,结果见图3,其中,浅灰柱子表示设计变量对设计目标产生正效应,深灰柱子表示负效应。从图3可知,Y向和Z向的滚珠丝杠导程、Y轴和Z轴的位置环增益对ε、ez和ex的影响较大,其他设计变量对设计目标的灵敏度均低于10%。由此可见,在机床设计、优化及控制过程中应更多地关注丝杠导程及位置环增益。
2 响应面模型构建及其拟合精度检验
2.1 响应面模型的构建
为提高响应面精度,选取精度较高的含交叉项的二次多项式进行各响应面拟合:

式中:f——拟合目标;
xi、xj——设计变量;
xi2——设计变量的非线性作用;
xixj——设计变量的耦合作用;
n——变量数目;
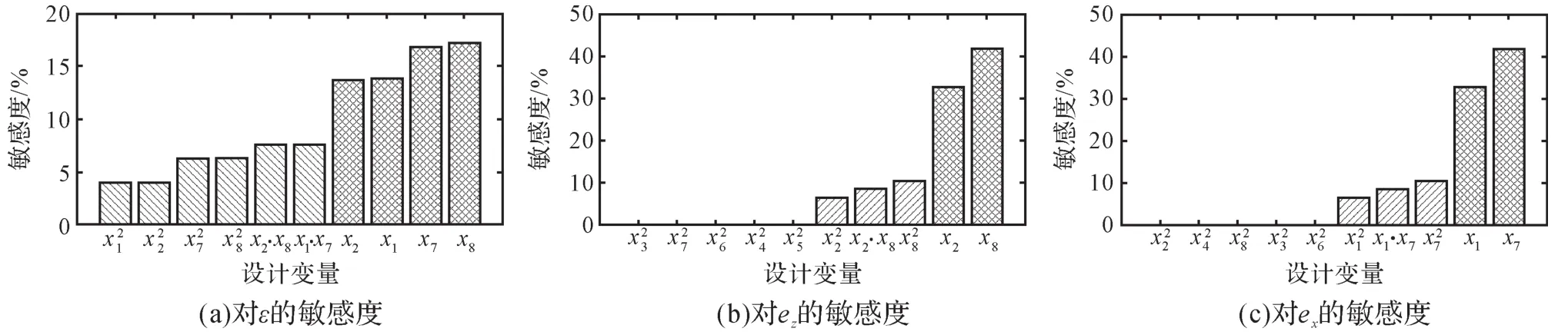
图3 各设计变量对设计目标的灵敏度Fig.3 Sensitivity of design variables to design objectives
a0,ai,aii,aji——待定系数。
利用式(2)将表3的数据进行二次多项式拟合,可以获得双轴联动进给系统轮廓误差和Z轴、X轴跟踪误差的响应面模型fε、fz、fx,分别如式(3)至式(5)所示。

2.2 响应面模型拟合精度的检验
将多重决定系数R2和修正的多重决定系数Radj2作为评价指标对已构建的响应面模型的拟合精度进行评价。R2和Radj2的值越接近于1,表明响应面模型的拟合精度越高。

式中:SSE——试验的残差平方和;
SST——试验的总平方和;
k——试验次数。
经计算,各响应面模型拟合精度的评价指标如表4所示。双轴联动进给系统轮廓误差和单轴跟踪误差的拟合曲线如图4所示,设计目标对部分设计变量的三维响应面如图5所示。由表4和图4可知,响应面模型的拟合精度较高,因此,所建立的响应面模型准确。

表4 各响应面模型拟合精度的评价指标Table 4 Evaluation indexes of fitting accuracy of each response surface model
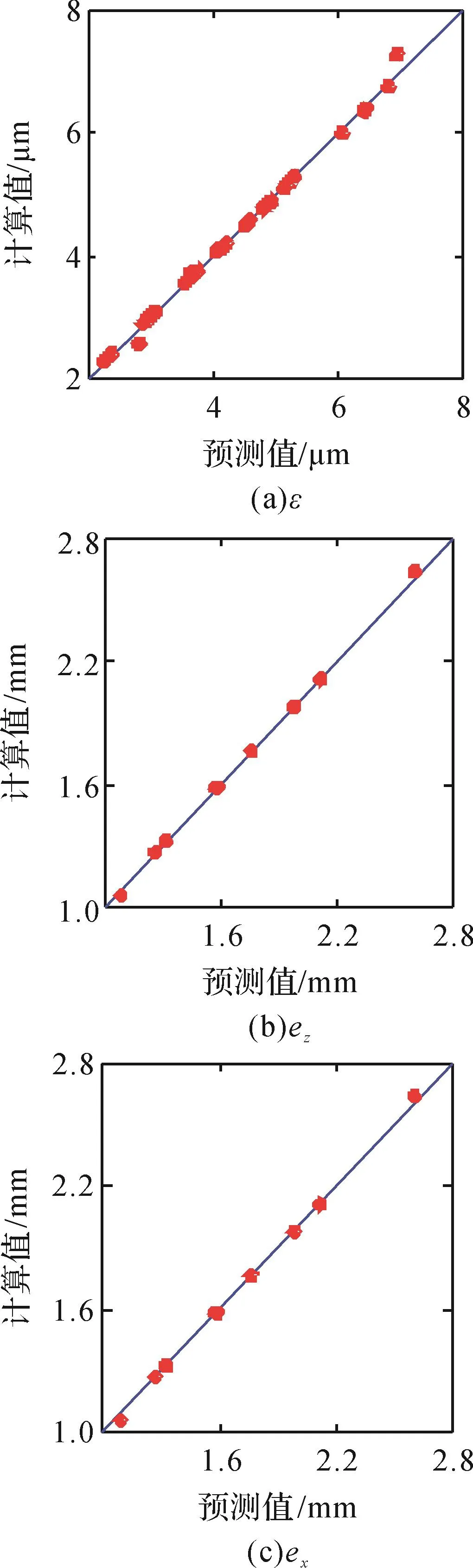
图4 双轴联动进给系统轮廓误差和单轴跟踪误差的拟合曲线Fig.4 The fitting curves of contour error and uniaxial tracking error in biaxial linkage feed system
3 双轴联动进给系统的优化
采用多目标优化遗传算法NSGA-II对双轴联动进给系统进行优化设计。NSGA-II的参数设置如表5所示。经过NSGA-II优化,可得双轴联动进给系统的Pareto最优解集,如图6所示。

表5 NSGA-II的参数设置Table 5 NSGA-II parameter setting
根据设计目标顺序在Pareto最优解集中选择设计变量的最优值,如图7所示。
双轴联动进给系统多目标优化的结果,如表6所示。由表6可知,优化后双轴联动进给系统的轮廓误差由 3.68 μm 降低到 1.48 μm,Z轴的跟踪误差由1.583 14 mm降低到1.083 37 mm,X轴的跟踪误差由1.583 14 mm降低到1.092 87 mm,三者降幅均超过30%,优化效果明显。

图5 设计目标对部分设计变量的三维响应面Fig.5 The 3D response surface of the design objective to some design variables

图6 双轴联动进给系统的Pareto最优解集Fig.6 Pareto optimal solution set of biaxial linkage feed system
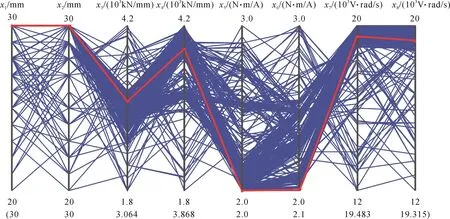
图7 双轴联动进给系统多目标优化的Pareto最优解Fig.7 Pareto optimal solution of multi-objective optimization of biaxial linkage feed system

表6 双轴联动进给系统多目标优化结果Table 6 Multi-objective optimization results of biaxial linkage feed system
优化结果表明,在机床设计阶段综合考虑机械结构参数和控制系统参数对机床轮廓误差和跟踪误差的影响,可以有效提高机床整机的动态设计精度,满足机床的设计要求,最终提高工件的加工质量。
4 结论
在前期研究的基础上,利用响应面法、灵敏度分析及遗传算法,以双轴联动进给系统的轮廓误差及Z轴、X轴的跟踪误差为优化目标,以滚珠丝杠导程、结合面轴向刚度、电机转矩系数和位置环增益等为设计变量,对双轴联动进给系统开展了多目标优化设计研究。结果显示,进给系统的结构参数及控制系统参数对优化目标的敏感度不同。因此,在实际优化过程中应根据不同的敏感度采取不同程度的优化。由对比优化前后双轴联动进给系统的轮廓误差及Z轴、X轴的跟踪误差可知,优化后各误差降幅均在30%以上,取到了良好的优化效果。机床实际运行过程较为复杂,双轴联动只是其工况之一,在后续工作中,将对三轴、五轴联动进给系统加工精度的影响因素展开研究,并通过实验对优化方法进行多方面验证。

