基于EEMD和分层阈值的磁记忆信号降噪方法研究
郑华林,王 超,潘盛湖,高炜祥
(西南石油大学机电工程学院,四川成都610500)
金属管道被广泛应用于油气的传输。伴随金属管道使用年限的增加而出现的管道应力集中现象会对其正常运行造成重大影响。因此,提前检测出管道应力集中的准确位置是保证管道正常运行的关键[1]。由于金属磁记忆检测方法是基于在地磁场中铁磁制品应力集中区域所产生的弱磁信号进行的,因此收集弱磁信号并对其信号特征进行分析是判断金属管道缺陷位置的关键[2-3]。
利用金属磁记忆检测技术对金属管道进行早期诊断不需要对管道进行清洗和预处理,可以实现在线检测。相较于传统的检测方法,该方法是通过对收集的弱磁信号的分量梯度值进行分析和判断,实现管道缺陷位置的判断,为管道诊断提供了一种新的思路。张元良等[4]采用HMC1052磁阻传感器,设计了以DSP(digital signal processor,数字信号处理器)和CPLD(complex programmable logic device,复杂可编程逻辑器件)为控制核心的磁记忆检测仪,提高了弱磁信号的采集效率,但没有对收集的信号进行处理;马钢等[5]将EMD(empirical mode decomposition,经验模态分解)降噪与小波降噪进行了对比分析,发现EMD降噪能得到更好的信噪比,但是容易出现模态混叠的问题,导致对缺陷的位置产生误判;杨理践等[6]利用电磁感应原理设计了应力检测系统,并通过离散小波变换对收集的信号进行噪声分离,提高了信号的信噪比,达到了降噪的效果,但是缺陷的特征信号不完整;孙华庆等[7]利用改进的EMD算法将有效磁信号从高斯噪声中提取出来,保证了缺陷特征信号的完整性,但是降噪效果不是很明显。
为此,笔者以磁阻传感器HMC1021、HMC1022为磁信号收集探头,设计了以STM32F407为控制核心的三维磁记忆检测系统,将总体平均经验模态分解(ensemble empirical mode decomposition,EEMD)算法和分层阈值降噪算法应用于磁记忆检测技术中,对收集的弱磁信号进行降噪,以有效降低噪声的干扰,保留缺陷特征信号的完整性,实现管道缺陷位置的在线检测。
1 金属磁记忆检测系统的设计
1.1 金属磁记忆检测的原理
由于疲劳和被腐蚀,金属管道极易出现变形,进而产生应力集中。研究表明,在地磁场中,铁磁性材料出现应力集中之后,其内部的磁畴会发生不可逆的重新取向,应力集中区域将形成类似漏磁场的分布[8]。当管道某区域存在应力集中时,其切向磁感应分量Hp(x)出现峰值,而法向磁感应分量Hp(y)符号改变且过零值点,如图1所示。通过检测其法向磁感应分量梯度,就可以判断出应力集中区域。
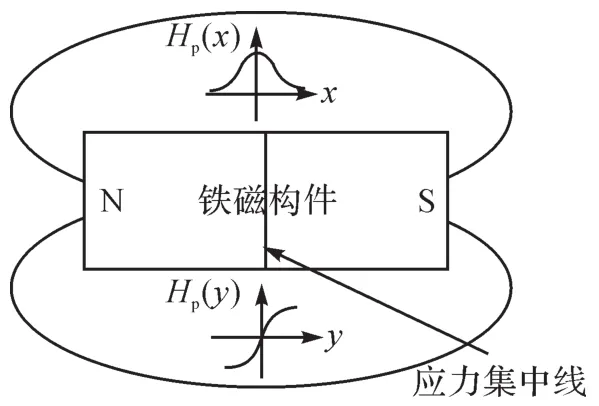
图1 金属管道应力集中区域磁场的特征Fig.1 Characteristics of magnetic field in stress concentration region of metal pipe
1.2 传感器探头的设计
传感器探头用来采集地磁场所激发的磁信号。由于磁信号非常微弱,因此能否捕捉到微弱的磁信号是磁记忆检测的关键[9]。由于地磁场的磁场强度H=0.5 A/m,而磁阻传感器的磁场强度检测范围为10-6~10 A/m,且其性价比较高,因此选取磁阻传感器为该检测系统的探头。
选用Honeywell公司生产的HMC1021、HMC1022磁阻传感器,用于采集三维方向的弱磁信号。该传感器的磁场强度检测范围为-6~6A/m,分辨率为85 μA/m10]。将2个传感器垂直放置,用于收集3个方向的磁场强度Bx、By、Bz相对x方向的分量梯度值。传感器1和传感器2分布在无磁外壳两端并固定,且均符合右手定则。传感器及其放置方式如图2所示。

图2 传感器及其放置方式Fig.2 Sensors and their placement modes
1.3 硬件结构的设计
金属磁记忆检测系统采用三维弱磁信号检测技术[11],其硬件结构如图3所示。其中:数据采集与数据处理模块间采用RS232串口通信方式,用于传输传感器所采集的磁信号;采用A/D转换芯片ADS1256将采集的模拟磁信号转换为数字信号;通过SPI(serial peripheral interface,串行外设接口)通信与控制核心完成信号传输,控制核心通过STM32F407芯片对信号进行处理;稳压电源为芯片提供5 V的电压;上位机用于数据分析。
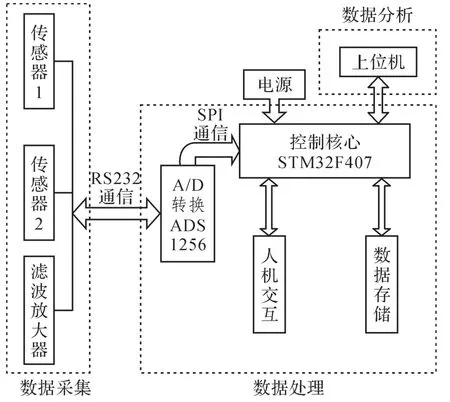
图3 金属磁记忆检测系统的硬件结构Fig.3 Hardware structure of metal magnetic memory detection system
2 磁信号处理算法
在检测过程中,受周围环境的影响,检测系统所采集的磁信号往往包含一些电磁噪声信号,导致有效特征信号的提取变得非常困难。为了消除电磁噪声的影响,须对信号进行预处理和降噪处理。
2.1 EEMD算法
EMD算法是由Huang等[12]提出的一种信号处理算法,主要用来处理非平稳、非线性的信号。该算法首先提取原始数据的极大值和极小值而形成包络线,然后利用包络线对信号进行分解,但是在分解的过程中容易出现模态混叠的问题。
针对这个问题,Wu等[13]在EMD算法的基础上提出了EEMD算法。该算法利用白噪声在进行模态分解时其均匀分布的频率按一定规律分解的特点,在对原始信号进行模态分解时,将白噪声引入原始信号,经过一次模态分解得到本征模函数(intrinsic mode function,IMF),再将不同的白噪声引入原始信号进行多次模态分解,最后将多次分解所得到的IMF取平均。其具体步骤为:
1)将白噪声信号w(t)引入原始磁记忆信号y(t),得到总体信号Y(t)。通过模态分解,将总体信号Y(t)分解成IMF分量,则:

式中:Ii(t)为模态分解后各IMF分量;In(t)为磁信号的余项;n为当In(t)足够小时,其原始信号的分解次数。
2)将不同的白噪声信号wj(t)引入原始信号y(t),得到总体信号Yj(t),通过模态分解,可得:

式中:Iij(t)为引入不同白噪声后的各IMF分量;Ijn(t)为引入不同白噪声后磁信号的余项。
3)将分解得到的各IMF分量进行总体平均求解,以消除白噪声引入所带来的影响,得到更加真实的IMF分量。最终的降噪信号y1(t)为:
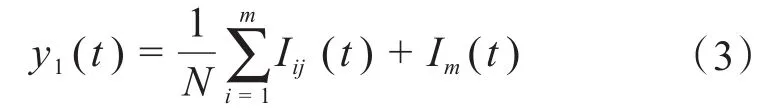
式中:N为引入不同白噪声的次数;Im(t)为磁信号的余项;m为当Im(t)足够小时,其原始信号的分解次数。
通过引入不同的白噪声对原始信号进行多次模态分解,可以解决模态混叠的问题。因此,本文采用EEMD算法对磁信号进行预处理。
2.2 分层阈值降噪算法
通过小波降噪可以对非平稳、多频率的有效频域信号进行提取。本文所处理的信号是微弱磁信号,因此,采用阈值降噪的方法对信号进行降噪[14]。阈值降噪分为软阈值、硬阈值以及分层阈值降噪等。软阈值降噪是通过一个确定的阈值对高频信号进行降噪处理,阈值的选取决定了降噪的优劣;硬阈值降噪能够保持信号的特征点,但是容易产生间断点,信号平滑度较差;分层阈值降噪是通过计算得出每层频域的阈值,对每层信号分别降噪,得到的信号平滑度较好,特征信号更明显。因此,本文选择分层阈值降噪算法对磁信号进行降噪。
为了衡量降噪效果,使用基于均值的信噪比SNR、均方根误差RMSE以及平滑度R对降噪效果进行评价。其中:SNR和R越大,表明有效特征信号的占比越大,降噪效果越好,RMSE则反之。SNR、RMSE、R可计算如下[15]:

式中:L(t)为阈值降噪后的信号;(t)为阈值降噪后信号的均值;t为信号的采样点数;h为采样长度。
2.3 信号处理算法的步骤
由于收集的磁信号是无规律、多变的,信号经过EEMD算法分解所得到的各IMF分量中的一些特征信号极有可能包含有效的特征信号,因此经过EEMD预处理后所得到的重构信号可能存在特征信号缺失的情况。为了保证信号的完整性而又达到降噪的目的,笔者提出了一种基于EEMD和分层阈值降噪(以下简称为EEMD分层降噪)的信号处理算法。算法的结构如图4所示。

图4 EEMD分层降噪算法的结构Fig.4 Structure of EEMD layered noise reduction algorithm
磁信号处理算法的步骤如下:
1)将白噪声信号w(t)引入原始信号y(t),经过多次EEMD后得到若干IMF,再将得到的各IMF分量进行总体平均求解,最终得到所需的IMF分量I(t)[16],即:

其中N可由式(8)确定:

式中:S为白噪声幅值标准差与原始信号幅值标准差之比;A为白噪声的幅值系数。
求解出一次重构信号E(t):

2)通过相似度指标选择E(t)的最佳分解层数,即将分解后的重构信号E(t)与原始信号y(t)作标准偏差,得到均方误差u。由于均方误差可能为零,需要对其进行归一化处理,记为u',其值范围在0~1之间。u'值越接近1,一次重构信号与原始信号y(t)的相似度越高[17],即:

3)初步选择最佳分解层数,并对IMF进行频谱分析。首先将信号进行傅里叶变换,得到傅里叶级数系数Fb,然后通过自相关函数计算求得所需的功率谱P(w)[18],即:

式中:T为周期;δ为频谱函数;w为谐波频率;w0为初次谐波频率。
根据功率谱判断各IMF分量在该频域下的能量因子大小。功率谱中的能量因子越大,说明该IMF中所含的有效特征信号越多。
4)通过频谱分析和相似度计算,确定EEMD的最佳分解层数,并对该层数下所有的IMF分量进行阈值降噪,得到降噪后的分量。
5)将EEMD后所得的重构信号E和降噪后的Xi分量进行二次重构,得到最终的降噪信号y1(t),即:

3 EEMD分层降噪仿真分析
3.1 不同信噪比的仿真信号的EEMD分层降噪
为了对EEMD分层降噪的效果进行定量评价,本文以正弦信号作为仿真信号进行降噪分析[19]。根据实测环境噪声,将仿真信号中白噪声的噪声强度设为15 dB,引入白噪声后仿真信号的信噪比分别为2,5,10 dB,如图5所示。
通过对EEDM参数的多次分析与总结,确定S=0.3,N=10。以SNR=2 dB为例,EEMD分层降噪仿真结果如图6所示。
表1为仿真信号在EEMD分层降噪前后信噪比的对比。分析表1可知,随着原仿真信号信噪比的加大,EEDM分层降噪前后信噪比的差值逐渐减小,表明该方法对信噪比较小的含噪信号较为适用。

图5 不同信噪比的仿真信号Fig.5 Simulated signal with different SNRs

图6 EEMD分层降噪仿真结果(SNR=2 dB)Fig.6 Simulation result of EEMD layered noise reduction(SNR=2 dB)
3.2 EEMD分层降噪与小波阈值降噪效果的对比
为了验证EEMD分层降噪的效果,采用小波硬阈值和小波软阈值降噪,并将结果与EEDM分层降噪进行对比。采用原信号信噪比为2 dB的仿真信号,选取sym4小波基对该信号进行4层小波分解,降噪结果如图7所示。由图7可知,EEMD分层降噪的效果更好。

表1 仿真信号在EEDM分层降噪前后信噪比的对比Table 1 SNR comparison of simulation signals before and after EEDM layered noise reduction单位:dB
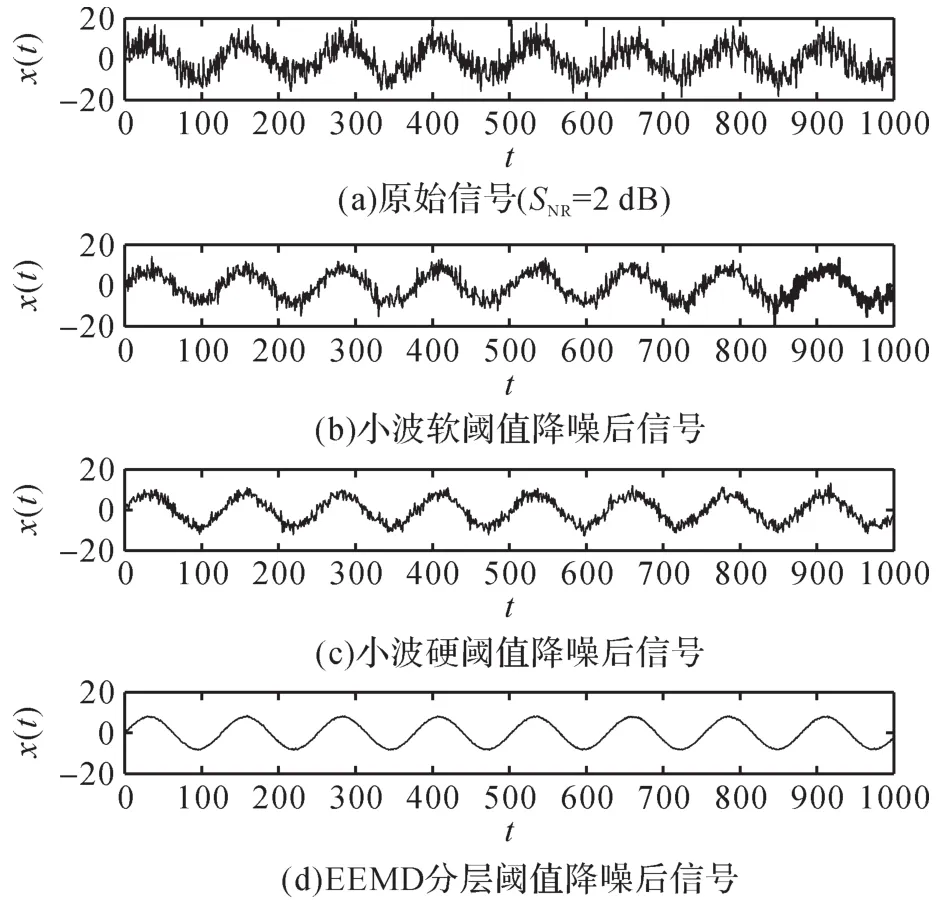
图7 EEDM分层降噪和小波阈值降噪结果的对比Fig.7 Comparison of results between EEMD layered noise reduction and wavelet threshold noise reduction
用SNR、RMSE以及R对EEMD分层降噪和小波阈值降噪效果进行定量评价,如表2所示。由表2可知,EEMD分层降噪后,信号的信噪比和平滑度较大,均方根误差较小。因此,相比于传统的小波阈值降噪,EEMD分层降噪的降噪效果更好。

表2 EEDM分层降噪和小波阈值降噪效果的定量评价Table 2 Quantitative evaluation of the effect of EEMD layered noise reduction and wavelet threshold noise reduction
4 EEMD分层降噪实验
4.1 实验方法
本实验采用笔者设计的金属管道三维弱磁信号检测仪器,试件采用20#无缝钢管。人为对该钢管设置2个缺陷,形成缺陷区域。设管道走向为Y轴方向,将检测仪器水平放置,在检测过程中与管道垂直,沿Y轴采集试件磁信号的水平梯度数据。钢管的检测方式如图8所示。

图8 钢管的检测方式Fig.8 Detection mode of steel pipe
4.2 实验结果
将采集的磁信号进行EEMD预处理,其中设S=0.3,N=10。EEDM前后钢管磁信号的磁场强度如图9所示。从图可见,模态分解后在缺陷位置的磁场强度的幅值变化最显著。
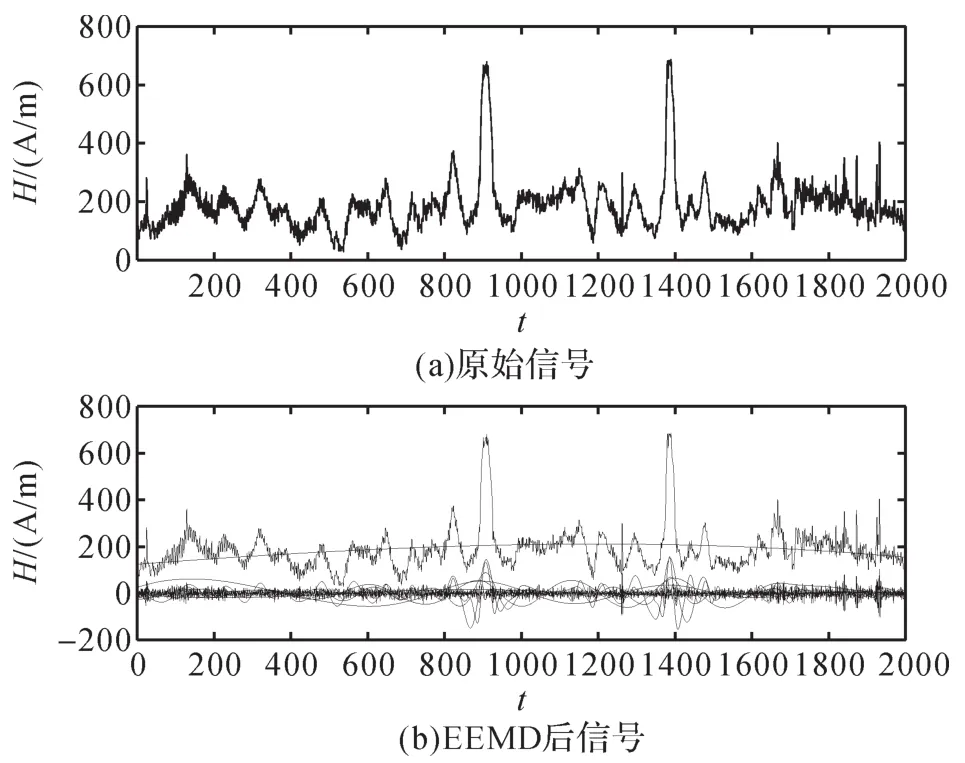
图9 EEDM前后钢管磁信号的磁场强度Fig.9 Magnetic field intensity of magnetic signal of steel pipe before and after EEDM
对得到的各IMF进行频谱分析和相似度计算,结果如图10所示。其相似度在第6阶后基本不变,且前6阶IMF分量能量因子都较大,因此其最佳分解层数为6层。
采用分层阈值算法对该磁信号进行降噪,选取sym4小波基,对该信号进行4层小波分解。降噪前后钢管的磁信号如图11所示。由图11可知,EEDM分层降噪对噪声的高频和低频信号有很好的抑制作用,并且保留了一些高频信号,使有效的特征信号更加明显,降噪效果更佳。
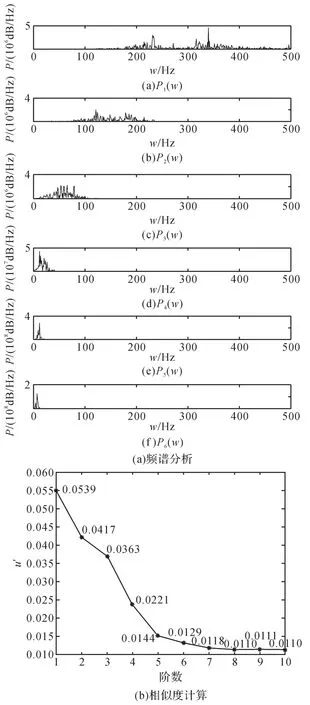
图10 钢管磁信号各IMF频谱分析和相似度计算结果Fig.10 IMF spectrum analysis and similarity calculation results of magnetic signal of steel pipe
5 结 论
本文提出了一种基于EEMD和分层阈值的磁记忆信号降噪方法。利用EEMD分层阈值降噪方法对含噪信号进行处理,并且根据频谱分析和相似度计算选择最佳分解层数,以此来提高磁信号的信噪比,同时抑制噪声的高频和低频信号。

图11 EEMD分层降噪前后钢管的磁信号Fig.11 Magnetic signal of steel pipe before and after EEDM layered noise reduction
通过仿真分析可知,EEDM分层降噪方法适用于信噪比较小的含噪信号,其降噪效果优于小波阈值降噪,适合弱磁信号的降噪。借助现场采集的弱磁信号对所提方法进行实验验证,结果表明,该方法能较好地保留特征信号,达到降噪效果。因此,在管道缺陷在线检测时,采用EEMD分层降噪方法对现场收集的磁信号进行降噪处理,能够有效降低噪声干扰,保证缺陷特征信号的完整性,实现管道的缺陷定位,为管道缺陷的在线检测提供了可行的方法。

