一种基于改进预测电流控制的Vienna 整流器设计
冯兴田,崔 晓,陶媛媛,王世豪
(中国石油大学(华东) 新能源学院,山东 青岛 266580)
三相Vienna 整流器拓扑在20 世纪90 年代被提出,因其开关器件较少、输出电压可调等优点成为现代电力电子领域研究的热点问题,并广泛应用在通信电源、风力发电、不间断电源和混合动力车充电站等领域[1-3]。目前,Vienna 整流器控制策略的研究得到了学者和工程师的广泛关注,多种控制策略被应用到整流器的控制中,并取得了一定的效果[4-6]。其中,文[7—9]采用了单周期控制方案,与传统的PI 控制相比,降低了电路复杂程度,提升了功率因数。文[10—12]在Vienna 拓扑中采用了直接功率滑模控制,虽然不需要同步旋转坐标变换,提升了动态响应速度,但仍需要PI模块实现空间矢量调制(SVPWM),增加了结构复杂性。
为了实现对工业过程的最优控制,20 世纪70 年代提出了模型预测控制MPC(model predictive control)的思想,因其对模型的精度要求不高,无须设计复杂的控制参数,在非线性问题的处理上得到了很好的发展和应用[13-15]。
本文针对三相Vienna 整流器,提出一种改进的预测电流控制,将有限控制集模型预测控制FCS-MPC(finite control set-MPC)的思想与SVPWM 相结合,使得预测控制器得到的最优开关状态经过调制器后生成开关信号,通过调整载波的频率来实现开关频率的控制,在保留模型预测控制优点的同时,固定了开关频率。同时,设计了三相Vienna 整流器的仿真和实验平台,进行了控制策略的研究。
1 三相Vienna 整流器的数学模型
图1 所示为本文采用的三相Vienna 整流器主电路的拓扑结构。ea、eb、ec为三相交流电源;ia、ib、ic为三相输入电流;L1、L2、L3为值为Ls的三相滤波电感;r1、r2、r3为值为r 的输入侧等效电阻;C1、C2为值为C 的直流侧上下电容;RL为输出电阻负载,其两端电压为直流母线电压Vdc。为了简化系统结构,假定所有功率开关器件为理想开关,S1、S2、S3为三相开关,每一个双向开关由2 个串联的MOSFET 模块组成。
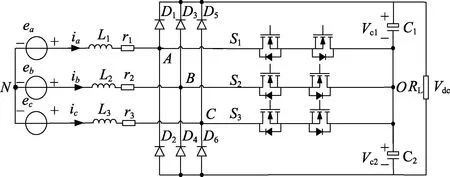
图1 三相Vienna 整流器主电路拓扑
定义Sij(i=a, b, c; j=1, 2, 3)为第i 相的开关函数,可视为3 个单刀开关,具体表示如下:
Si1=1 时,第i 相上桥臂二极管导通;Si1=0 时,第i 相上桥臂二极管关断;
Si2=1 时,第i 相开关管导通;Si2=0 时,第i 相开关管关断;
Si3=1 时,第i 相下桥臂二极管导通;Si3=0 时,第i 相下桥臂二极管关断。
因此Si1,Si2,Si3之间存在如下关系:
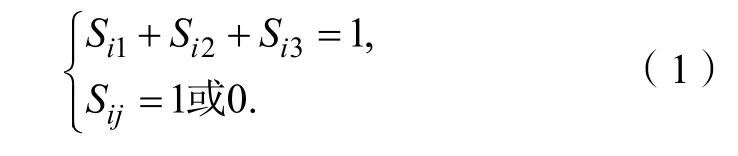
图1 所示的三相Vienna 整流器主电路数学模型可由以下微分方程表示:

式中,vAN、vBN、vCN分别为整流桥交流输入端对交流电源中点N 的电压。
为了进一步对控制策略进行分析,将三相abc 坐标系下的数学模型转化到两相旋转dq 坐标系下,可得到以下微分方程:

式中,ed和eq为变换后的交流侧输入电压;id和iq为dq 坐标系下的输入电流;vd和vq为dq 坐标系下整流桥交流输入端对交流电源中点N 的电压;ω 为角频率。
2 预测电流控制策略
有限状态预测控制是一类典型的非线性控制策略,假设采样周期为Ts,可将三相Vienna 整流器的数学模型离散化表示为
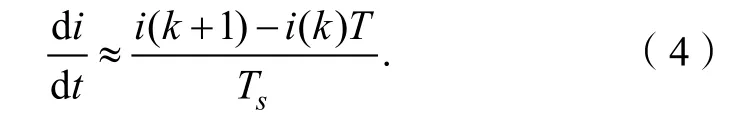
因此,k 时刻两相旋转坐标系下的输入电流,即式(3),在离散化后可被表示为
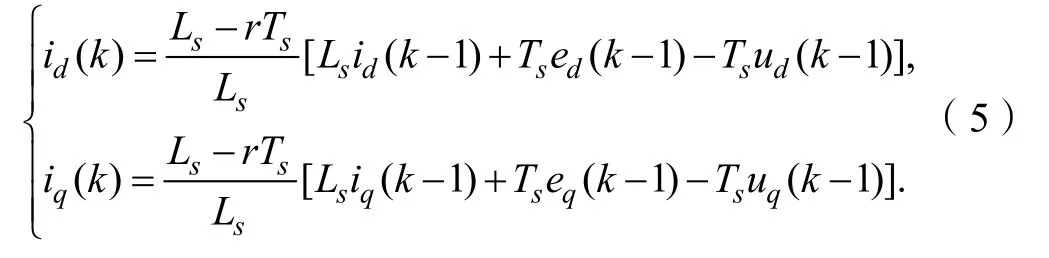
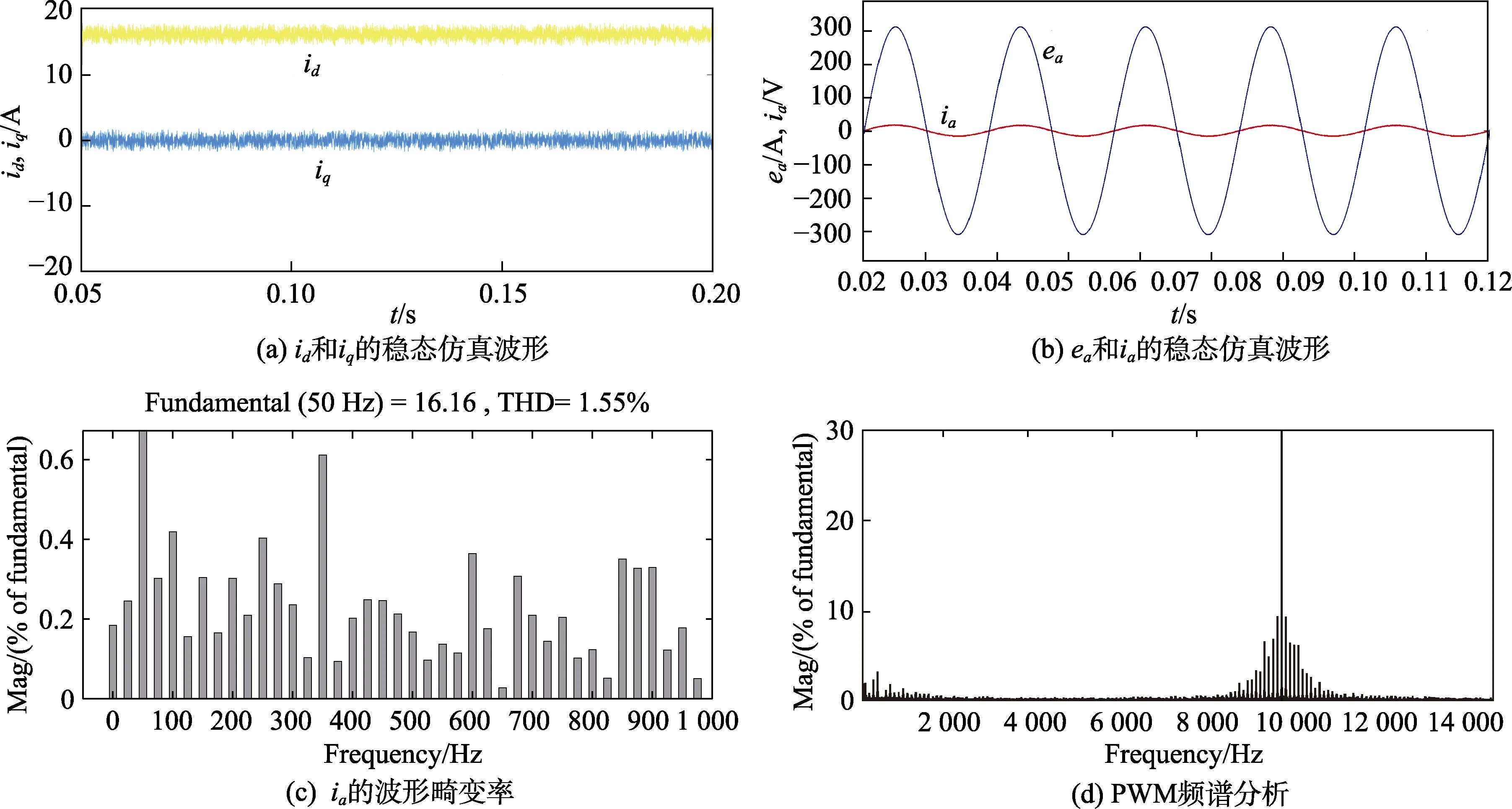
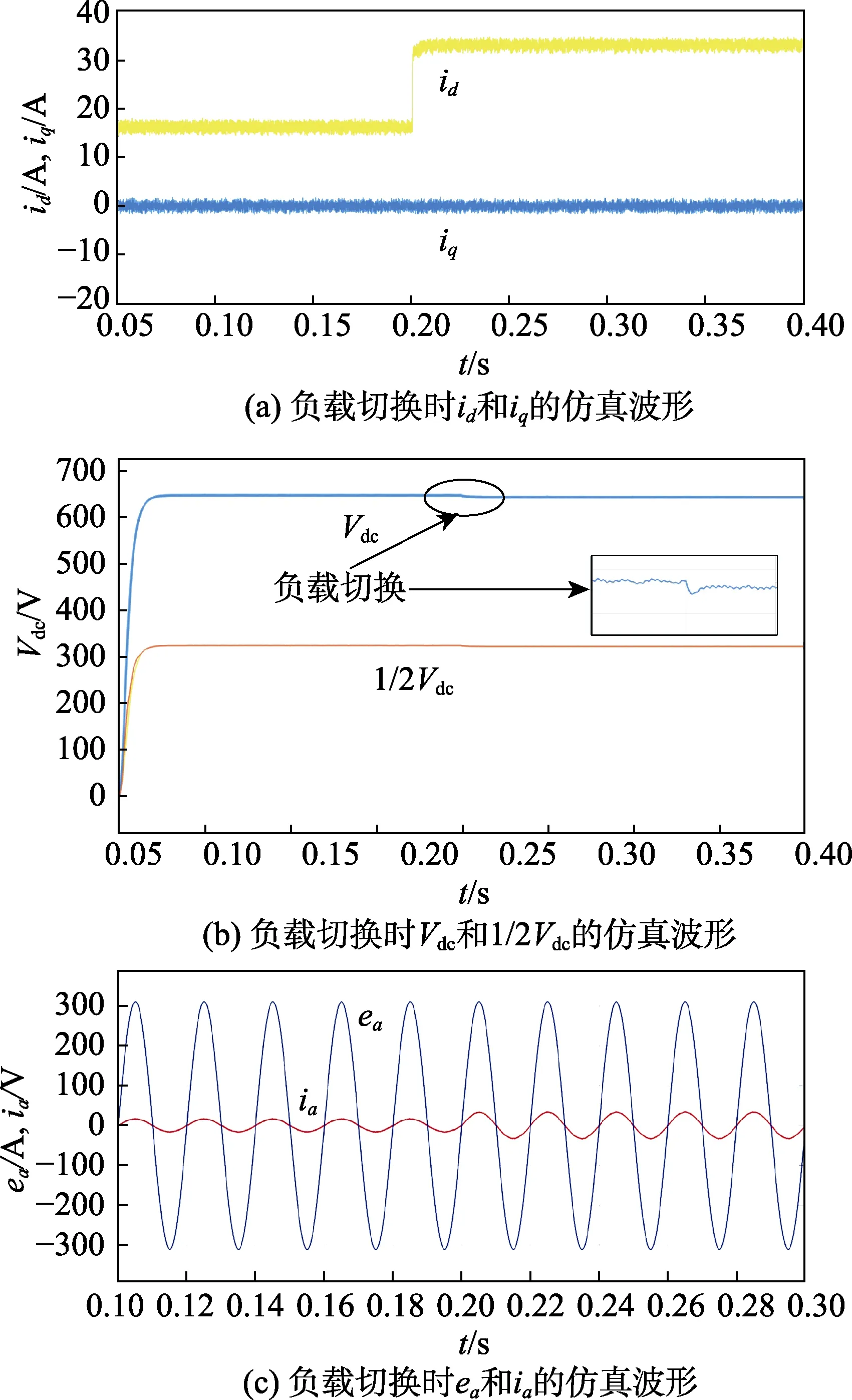
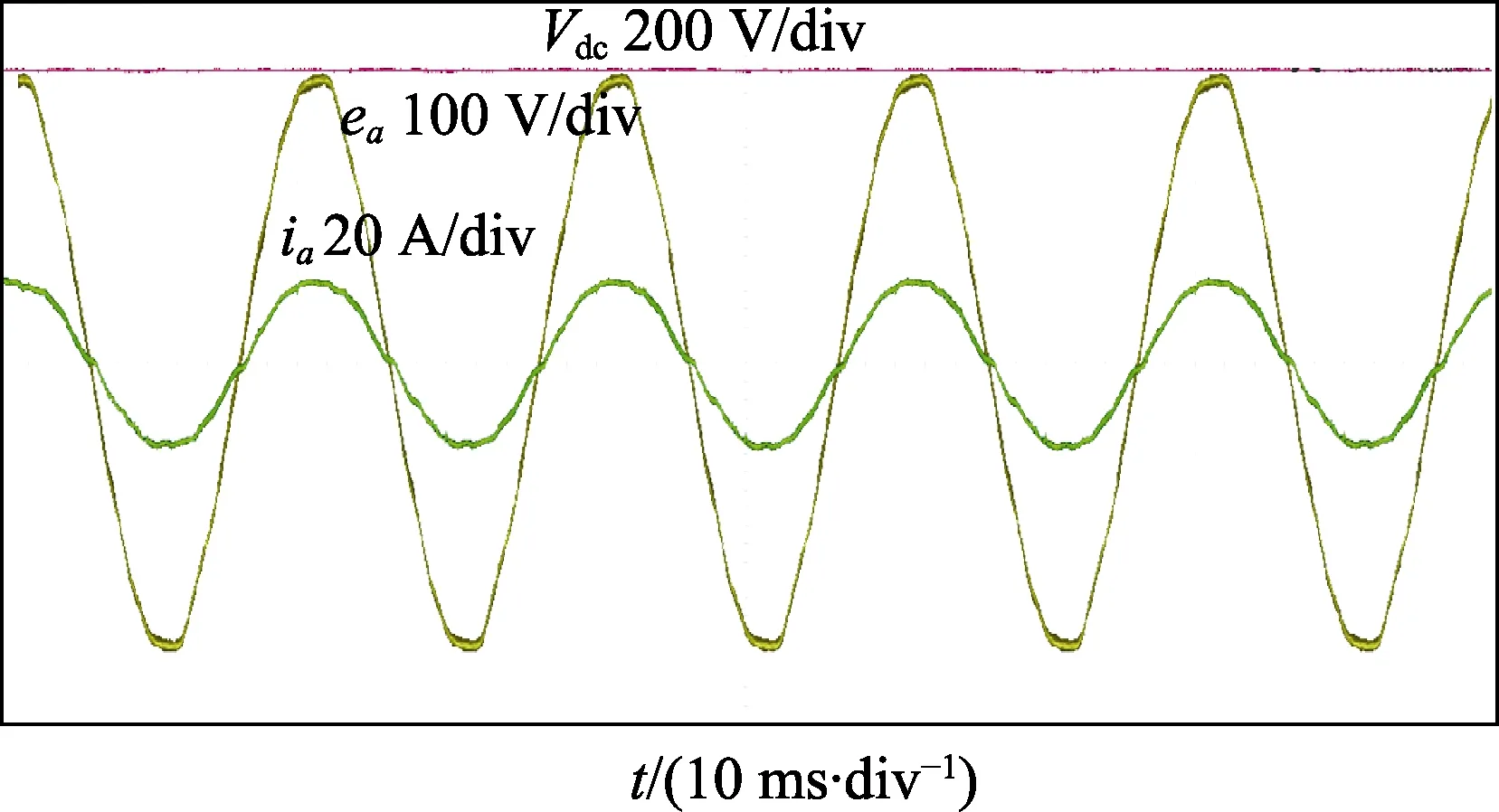
式中,ud=vd+ωLsiq,uq=vq-ωLsid。在采样间隔足够小并且有Ls< i(k)为k 时刻的输入电流采样值;i(k+1)为k+1 时刻的电流预测值;e(k)为k 时刻电网电压预测值。 本文提出改进的预测电流控制方案如图2 所示。基本思想是在每个开关周期的初始计算整流器平均电压矢量,同时在开关周期结束时消除输入电流矢量分量的跟踪误差。接下来,将输出矢量经过空间矢量调制的方法计算出变换后的平均电压矢量并作用于系统。 图2 改进的预测电流控制策略框图 如果假设采样周期Ts与电源电压的周期相比较小,则假设分量ed和eq在周期Ts上恒定。 控制系统的目的是通过强制使下一个采样时刻的输入电流矢量等于所需的参考值,即:如图2 所示,从外部给出恒定的参考值,为了实现单位功率因数,使得。所以,可以假设: 将式(8)、式(9)代入式(6),则可得到如式(10)所示的控制矢量: 其中,εid和εiq分别是输入电流分量id和iq的实际跟踪误差,(k)是给定参考值的实际变化。可得到在切换周期结束时允许消除2 个输入电流矢量分量的跟踪误差的所需整流器平均电压矢量: 为了实现空间矢量调制,将得到的电压矢量经过坐标变换,从两相旋转dq 坐标系转换成两相静止坐标系αβ 形式: 式中,vα(k)、vβ(k)为两相静止坐标系下的平均电压矢量,即预测控制器所得到的最优开关控制状态。将其作为SVPWM 的输入信号经过调制单元后生成开关信号,通过调整载波的频率来实现对开关频率的控制。改善了传统FCS-MPC 控制策略下开关频率不固定的缺陷,提高了系统稳定性。 为了验证所提出的改进控制策略对于三相Vienna 整流器拓扑结构的有效性,在Matlab/Simulink仿真环境下建立了仿真模型,系统所用的仿真参数如表1 所示。 表1 仿真参数 图3 表示采用改进预测电流控制策略时系统的稳态仿真波形。由图3(a)可以看出,整流器受控电流矢量分量id和iq是恒定的,并且非常接近其参考值,iq平均等于零;图3(b)表示输入电压ea和输入电流ia的关系,保证了系统单位功率因数运行;图3(c)表明输入电流接近正弦波形,其波形畸变率仅为1.55%;从图3(d)的PWM 频谱分析,可以看出其谐波频率集中在采样频率10 kHz 附近,具备恒定的开关频率,在一定程度上可以提升系统运行的稳定性。 图3 改进的预测电流控制策略下稳态仿真波形 图4 是负载发生突变时的仿真波形,负载在0.2 s时由半载切换为满载,由图4(b)可以看出输出电压虽然有较小的波动,但可以在0.01 s 内恢复到给定值;输入电流波形从图4(c)看出,在负载切换时输入电流产生了微小畸变情况,但始终跟随输入电压波形并达到新的稳定状态,表明预测控制应用在电流内环可以保证系统以单位功率因数运行。 图4 负载切换时的仿真波形 设计开发了如图5 所示的Vienna 整流器样机,实验参数与仿真参数一致,如表1 所示。系统主电路由三相滤波电感、不可控二极管、SiC MOSFET 以及母线电容组成,控制电路采用DSP28035 为核心进行硬件设计,并实现控制策略的软件开发。 图5 Vienna 整流器实验样机 由图6 的稳态波形可以看出,稳态电压稳定在给定值650 V,同时能够保证输入电压和电流的同相位;网侧输入电流具有较小的谐波畸变率,波形质量良好。 图6 Vienna 整流器稳态波形 图7 是负载切换时的实验波形,可以看出负载由13 A 切换到6.5 A 时输出电压波动微小,并迅速稳定到给定值;输入电流在经过短时的微小畸变情况之后,重新达到稳定状态,表明控制策略的良好动态性能。 图7 负载切换时采用改进算法的实验波形 本文将预测控制与空间矢量调制相结合,实现了恒定开关频率的三相Vienna 整流器的控制器的设计。设计基于两相旋转dq 坐标系,直接输入电流矢量,电流回路中不需要添加滞回比较器或PI 控制器,提升了系统稳定性,降低了网侧谐波。设计使预测控制器得到的最优开关状态,经过调制单元后得到开关信号,通过调整载波的频率实现了开关频率的控制。

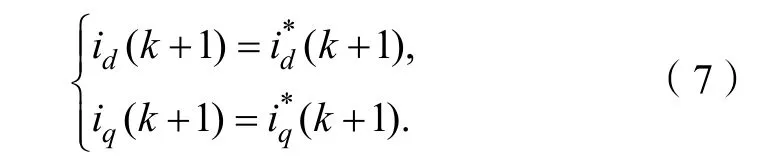

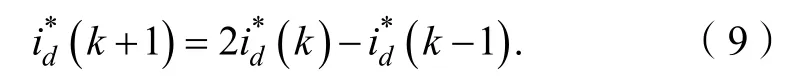

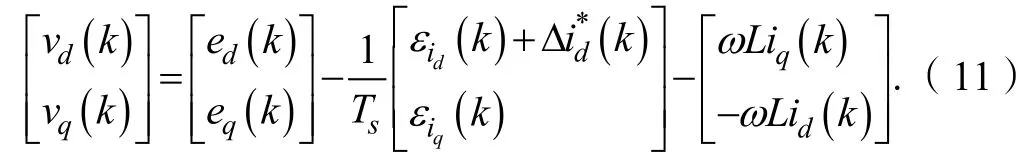

3 仿真与实验
3.1 仿真分析

3.2 实验结果


4 结论

