基于统计学方法的南方某市管网水水质特征研究

程郅涵，靳军涛，张金松，

(1.哈尔滨工业大学(深圳)，深圳 518055；2.深圳市水务(集团)有限公司，深圳 518031)

城市水厂出厂水经过庞大供水管网系统后水质受到不同程度的二次污染，造成用户龙头水处存在水质不达标的风险[1]。有效提升供水管网水质安全保障水平已成为供水企业关注的重点，为此各供水企业建立了系统的管网水水质监测体系，积累了大量的管网水监测数据。由于水质指标种类多，数据量大，且管网水水质影响因素复杂，如何采用科学方法对水质指标进行降维，删繁化简，提高数据利用水平是目前需要解决的问题。本研究以南方某市近 4 年供水管网末梢水水质监测数据为研究对象，借助 SPSS 软件，采用主成分分析法和对应分析法对管网末梢水质进行了时空变化、主要响应指标及指标相关性等方面的解析，以期提高监测数据利用效率，指导供水管网水质安全保障工作。

1 材料与方法

1.1 水质数据来源

该市供水企业采用HACCP体系方法建立了从源头到龙头的水质监测体系，其中针对管网末梢水采用人工采样检测和在线自动检测两种方法。人工采样检测共设有200个采样点，检测类别包括常规检测、月检测及半年检测，常规检测包括10项指标，每月2次；月检测指标包括42项，每月1次；半年检测包括指标106项，每年2次。在线检测主要针对余氯、浊度等4项指标，实时检测，每15 min上传一次数据。本研究数据来源自人工采样检测中的常规检测数据。同时综合考虑采样点覆盖地域和所属水厂的广泛性和代表性，从200个采样点中选择南山工区、西丽、下梅林等采样点，所选采样点基本信息如表1所示。

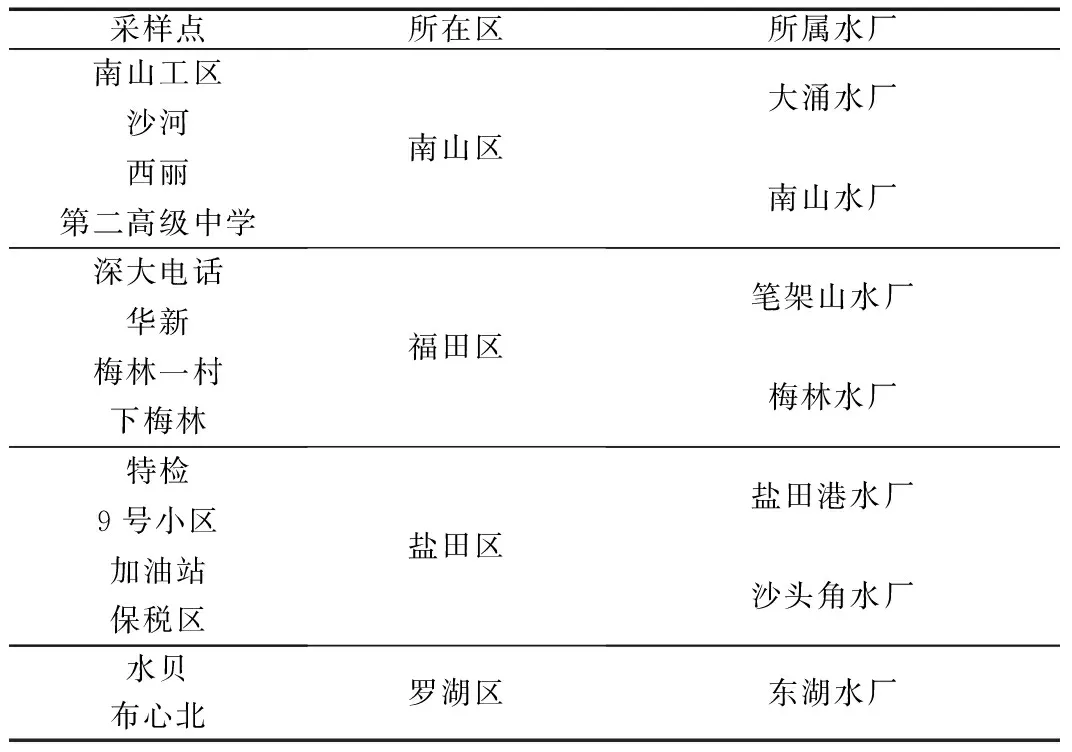
表1 采样点基本信息

采样点所处地理位置如图1所示。

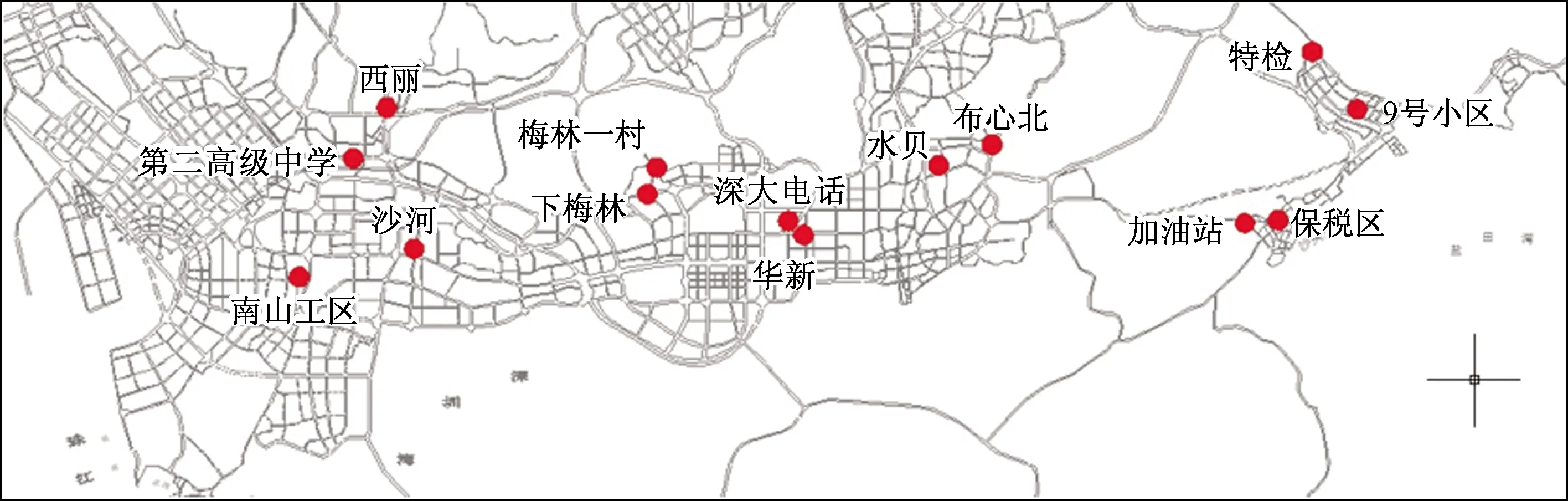
图1 采样点地理位置Fig.1 Geographical location of the sampling sites

1.2 水质特征研究方法

1.2.1主成分分析法

主成分分析法(Principal Component Analysis)是一种考量多元数据相关性、共同影响性的数学统计方法。在保证必要原始信息覆盖率前提下，用少数几个综合变量揭示原有多个变量间的内部结构，提炼出的综合变量被称为主成分[2]。

该方法基本思想可概括为通过正交变换将一组存在不同程度相关性的变量转换为一组线性不相关的变量。在几何上表现为将原有变量坐标系变换成新正交坐标系，并使之指向样本点最密集的p个正交方向，然后对多维变量系统进行降维处理，用原有变量的z(z≤p)个线性组合解释原有数据集信息[3]。

1.2.2对应分析法

对应分析法(Correspondence Analysis)也被称为关联分析或R-Q因子分析，是一种定性分析多元变量内在关联的统计分析方法，主要通过分析由不同种类变量构成的交互汇总图揭示原始变量间的联系[4]。

该方法基本思想可概括为在低纬度空间中以点的形式表示原始数据集列联表行和列中各变量的比例结构。进行R、Q因子分析的协方差矩阵A、B具有相同的主因子方差贡献，这是不同种类变量能够在一张因子荷载图中展示的内在核心[5-6]。直观性和便捷性是对应分析最主要的特点。

1.2.3具体操作流程

利用 SPSS19.0 软件进行主成分分析时，具体操作流程[7]可归纳为：

1)确定分析数据集，本文选取 pH、耗氧量、 Fe、总氯、氨氮、硫酸盐、氯化物、总有机碳、浊度、硬度 10 项水质指标，南山工区、西丽等 14 个采样点每两个月采样一次，2014-2017年度336 组数据，剔除含缺失值数据，有效数据共计328 组。

2)数据标准化，消除多维数据间量纲差异，使其呈正态分布。

3)KMO(Kaiser-Meyer-Olkin)检验和 Bartlett 球形度检验判断原始数据集是否适宜进行主成分分析，一般认为 KMO 数值大于0.5，Bartlett 检验显著性小于 0.05 可以进行主成分分析。

4)确定提取主成分数量，综合考虑以下3个因素：①特征值λ大于1；②单一主成分信息贡献率至少5%～10%；③累计信息贡献率至少60%～70%。

5)求解主成分特征向量，综合考虑成分矩阵系数的单一变量解释性和总变量集解释性，尽量避免复杂数据结构和多个主成分同时解释一个变量的情况。

6)依据式(1)、式(2)、式(3)构建主成分评价表达式。

(1)

(2)

(3)

式中：aij为第i个原始变量和第j个主成分对应的成分矩阵系数；bij为主成分表达式中对应每个原始变量的特征系数；λj为第j个主成分的特征值；zxi为第i个原始变量标准化后的数据值；Zj为第j个主成分的分析值；Z为主成分分析最终的分析值。

利用 SPSS19.0 软件进行对应分析时，具体操作流程[7]可归纳为：

1)由原始数据集求解计算矩阵W，水质指标变量的协方差矩阵A和地点变量的协方差矩阵B完成对应分析数据前期准备，具体计算公式如式(4)、式(5)、式(6)所示。

(4)

A=WTW

(5)

B=WWT

(6)

式中：xi为每组数据的行和；xj为每组数据的列和；T为数据集的整和。

2)对矩阵A进行R型因子分析，对矩阵B进行Q型因子分析，选取前K个累计贡献率达70%～90%的主因子。

3)在同一因子荷载图上汇总R、Q分析结果。

4)因子荷载图解读。

2 水质特征研究

2.1 水质整体情况

选取 pH、耗氧量、 Fe、总氯、氨氮、硫酸盐、氯化物、总有机碳、浊度、硬度 10 项指标对管网水质整体情况进行分析[8]。

从达标情况看，除Fe外其余9项指标均满足国家生活饮用水供水标准(GB5749—2006)，Fe检测值分布极为集中，中位值为0.01 mg/L，但在南山工区、沙河、布心北采样点存在异常超标情况。pH值在6.8～7.8之间浮动，中位值为7.33，半数以上采样点中位值接近上四分位数，检测值呈现左偏态分布，水质状态呈现低碱性；总氯在各采样点间检测值波动较大，下梅林、梅林一村采样点总氯中位值达0.8 mg/L和0.69 mg/L，与之相比南山工区、沙河采样点总氯中位值只有0.33 mg/L和0.39 mg/L，但都高于国标管网末梢水总氯0.05 mg/L的规定下限；各采样点硫酸盐和氯化物检测值分布较为分散，中位值分别为9.63 mg/L和10.74 mg/L，远低于国标250 mg/L的规定上限；浑浊度除南山工区外分布集中，中位值0.14NTU，南山工区浑浊度检测值远高于其余采样点，最大值达0.95 NTU；硬度在各采样点中位值仅有39.3 mg/L，远低于国标450 mg/L的规定范围，属于低硬度水。

为进一步识别该市管网水特点，利用 Langelier 饱和指数和拉森比率 LR 对管网水水质化学稳定性进行分析[9]。指数定义如式(7)、式(8)所示，水质稳定性分析图如图2所示。

IL=pH-pHs

(7)

式中:pH为管网水的实际pH；pHs为管网水在碳酸钙饱和平衡时的pH，即饱和pH；

(8)

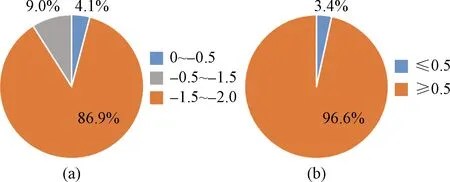
图2 管网水Langelier指数及拉森比率LR分布比例Fig.2 Langelier inder of water in pipe network and the distributon of Larson ratio

Langelier 指数是从热力学平衡角度出发，认为当水中碳酸盐处于过饱和状态，即IL>0时，管网水有结构倾向；当碳酸盐未饱和，即IL<0时，管网水有腐蚀倾向。由图 3 可以看出，全部采样点管网水Langelier指数均小于0，且86.9%的数值处于-0.5～-1.5之间，具有较强的腐蚀性。拉森比率LR是从水中腐蚀组分对缓蚀组分的比例出发，认为LR指数越低，水体腐蚀性越小，当LR<0.5时，水体腐蚀程度即可接收。仅有3.4%的管网水LR<0.5，96.6%的管网水拉森比率大于0.5，表明该市管网水具有较强的腐蚀性，存在阴离子穿透管道内壁腐蚀瘤，引发黄水的风险。

综上，该市管网水整体达标情况优良，其中不同采样点总氯含量波动大，部分采样点存在 Fe 超标和浊度异常波动现象，整体达标率在 99.9% 以上。通过水质稳定特性分析发现该市管网水具有低碱低硬度、水质化学稳定性较差、腐蚀性强的特点。

2.2 基于主成分分析法的水质评价

对数据集进行标准化处理，消除不同变量数据间的量纲差异。标准化后数据进行KMO检验和Bartlett球形度检验，得到KMO值0.688(>0.5)；Bartlett检验近似卡方值883.168较大，显著性Sig为0.00(<0.05)。表明数据集相关系数矩阵并非单位阵，原始变量间存在相关性，可以进行主成分分析及对应分析。

2.2.1主成分提取

利用SPSS软件，依据主成分提取的方差最大化原则，数据集方差及方差贡献汇总如表2所示。

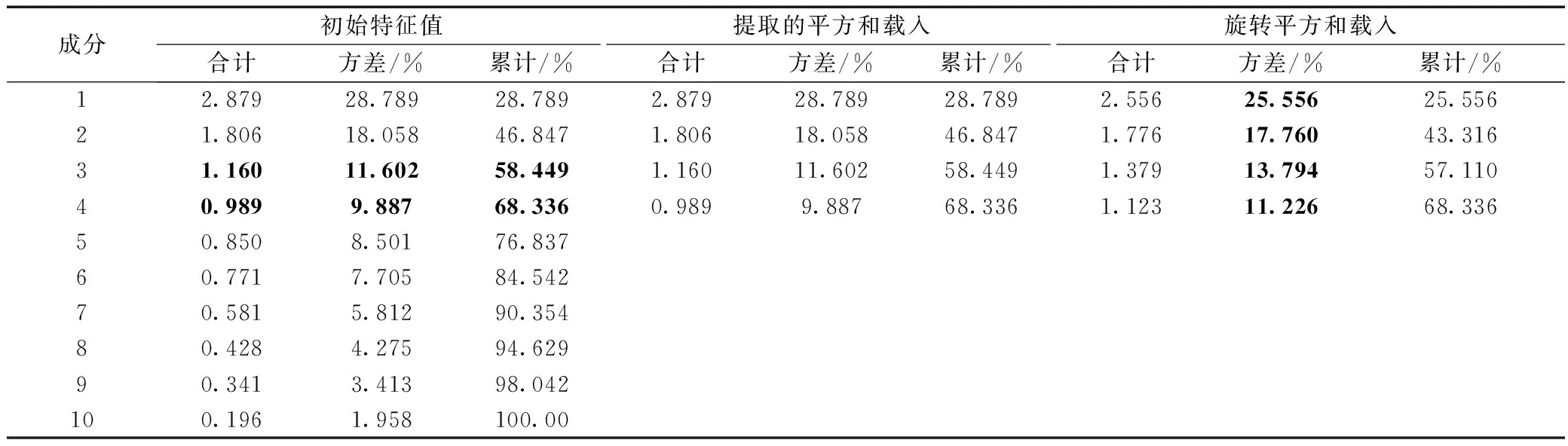
表2 主成分分析方差解释表

结合表 2 数据，综合考虑特征值λ大于1、单一主成分信息贡献率至少5%～10%、累计信息贡献率至少60%～70% 3方面因素，最终选取4个主成分变异替代原有9项水质指标，可覆盖解释原数据集68.336%的信息量。每项主成分与原始水质指标对应关系见成分系数矩阵表，即表3。该表可用于解释各个主成分变量的变异情况，系数绝对值越接近于1，表明主成分在该指标上的荷载越高，该指标越有可能成为管网水水质的主要评价指标。并借助Pearson相关系数法，对10项水质指标相关性进行定量检验，见表4。

由表3可得各主成分与高荷载原始变量间的对应关系，主成分1在硫酸盐、氯化物、硬度指标上具有较高荷载，覆盖原始数据集信息贡献率25.556%；主成分2在Fe、浊度、总氯指标上具有较高荷载，信息贡献率17.760%，第1、2主成分贡献比率值相较3、4主成分更高，对覆盖原始数据集信息具有很大贡献；不存在多个主成分在同一原始变量上荷载较高的情况，主成分解释性良好。根据某一主成分解释某一水质特征的性质，并结合表4 Pearson相关系数值(>0.5)，可以认为硫酸盐、氯化物、硬度之间，Fe、浊度、总氯之间，总有机碳和耗氧量之间具有相对其他水质指标更高的相关性。

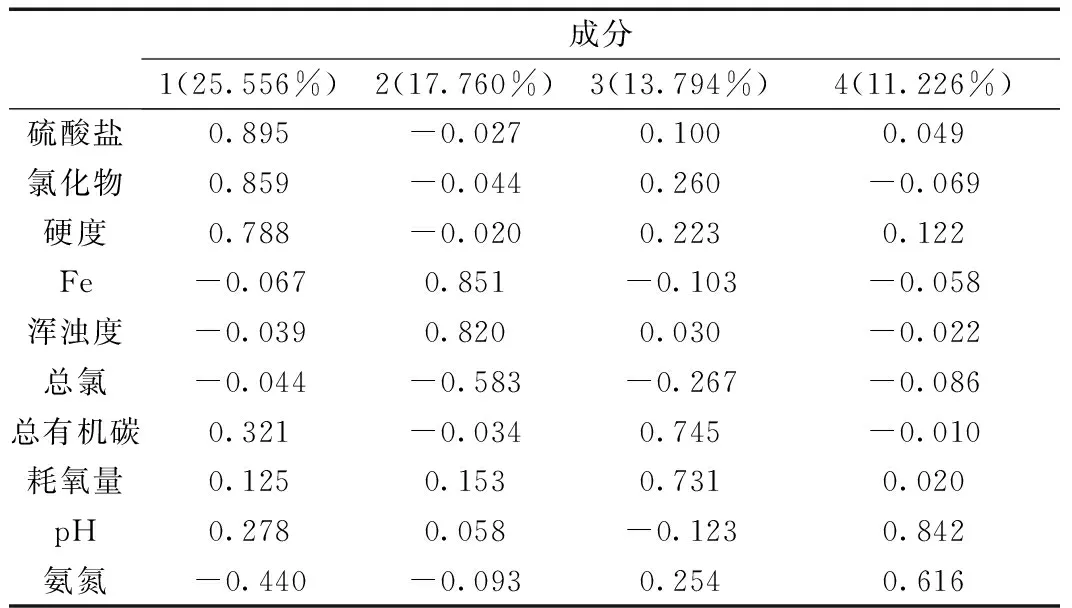
表3 成分矩阵系数表

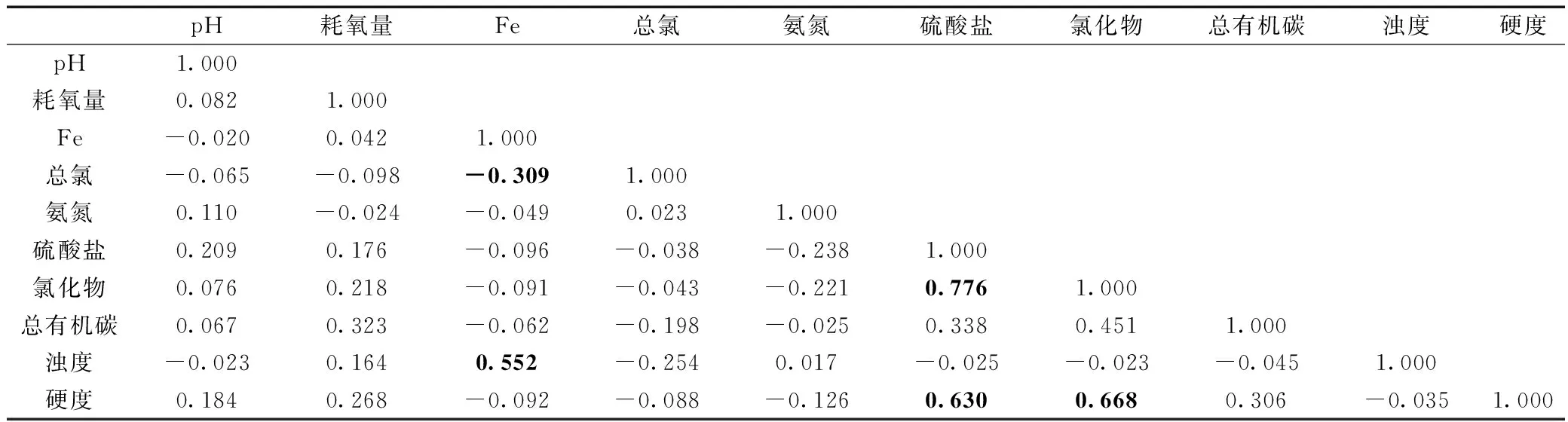
表4 水质指标间Pearson相关系数表

2.1.2水质评价

依据表3数据和公式(1)、式(2)、式(3)构建管网水水质主成分评价模型。最终分析值Z越小代表整体水质情况越好。不同年度及月份水质Z值变化如图4所示，不同采样点及其对应水厂覆盖区域Z值变化如图5所示。

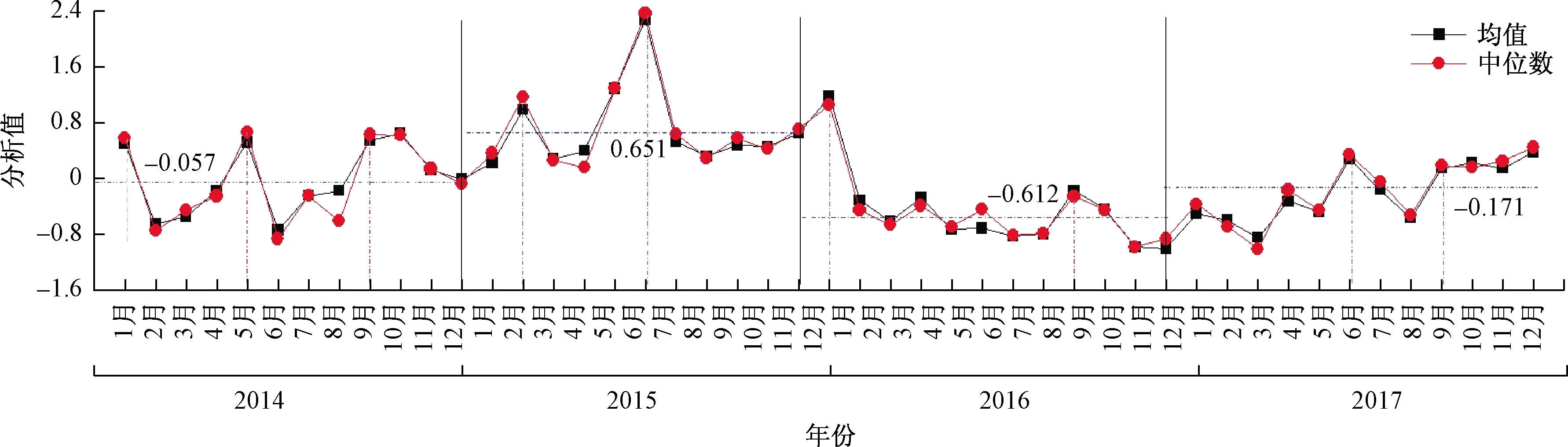
图3 不同年度及月份水质Z值折线图Fig.3 Line chart of Z value of water qualiky in different years and months

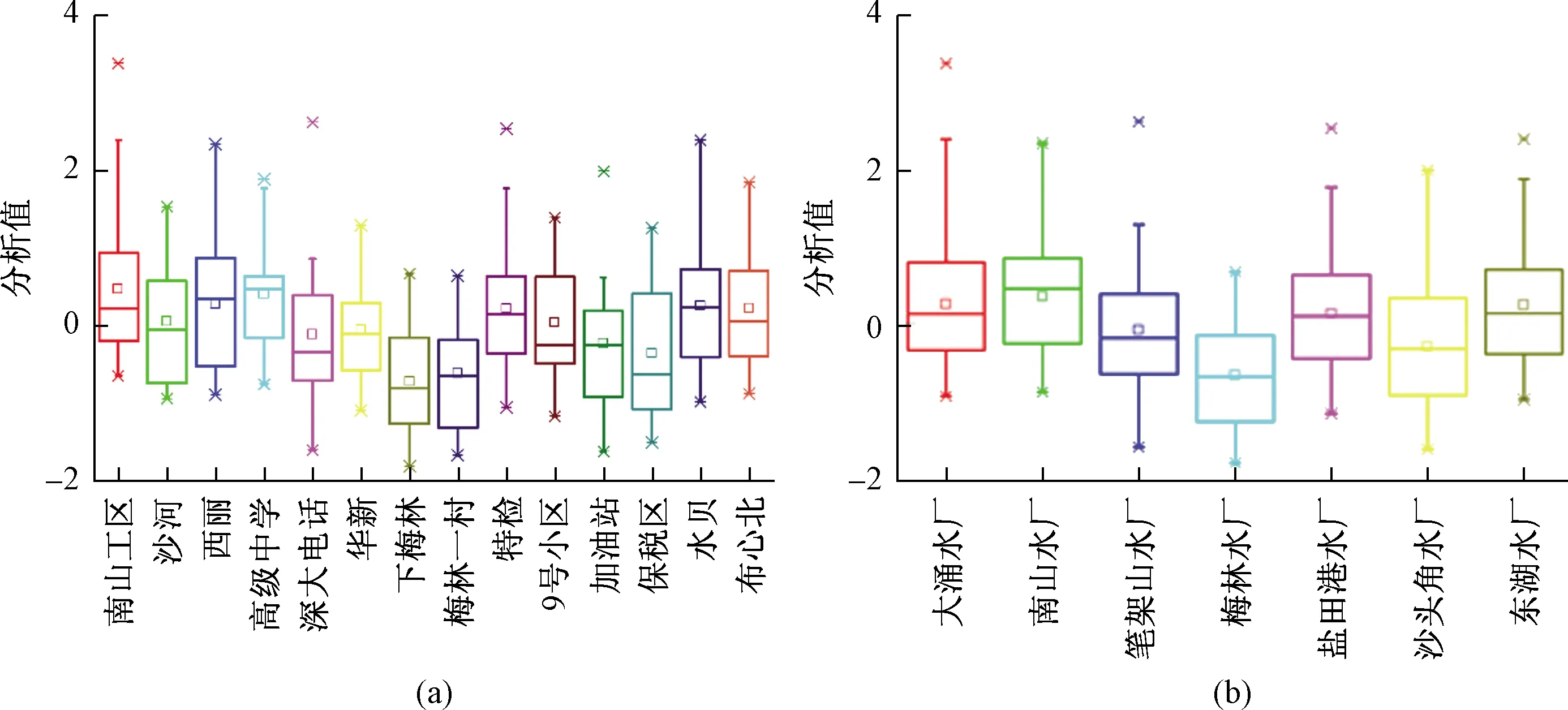
图4 不同采样点及其对应水厂覆盖区水质Z值箱型图Fig.4 Box plot of Z value of watter quality in different sampling sites and covering area of Corresponding water plants

从年度上看2016年全年分析值中位数为-0.612，且各采样点Z值均处于较低水平，整体管网水水质最优；2015年全年分析值中位数为0.651，各采样点Z值处于较高水平，或因多地管网改造工程引起的管网水转向、串并接等原因导致管网水水质稳定性变差，水质异常现象。从Z值波动情况看，2014—2017年间月Z值均值、中位数共出现陡增9次，其中6次“陡增”现象处于该市夏秋季节，这与我国南方地区夏季高温多雨、藻类大量滋生、面源污染相对严重，致使水源水水质较差现象相一致。

由图5可以看出，梅林水厂覆盖区下梅林和梅林一村采样点水质分析值最低，且4年间排名皆为第1，与其在优质饮用水改造工程中增加的“臭氧接触氧化+活性炭过滤”的深度处理工艺密不可分，其次排名前列的沙头角水厂覆盖区和笔架山水厂覆盖区也都在进行优质饮用水改造工程。而排名靠后的南山水厂覆盖区和东湖水厂覆盖区至今仍使用“混凝-过滤-沉淀”传统水处理工艺。

2.3 水质指标-采样点相关性分析

基于不同年度14个采样点10项水质指标中位值，依据式(4)、式(5)、式(6)构建协方差矩阵A、B，分别进行R、Q因子分析，在前两个主因子累计信息贡献率大于80%的情况下，在同一二维因子荷载图中展示分析内容，如图6所示。

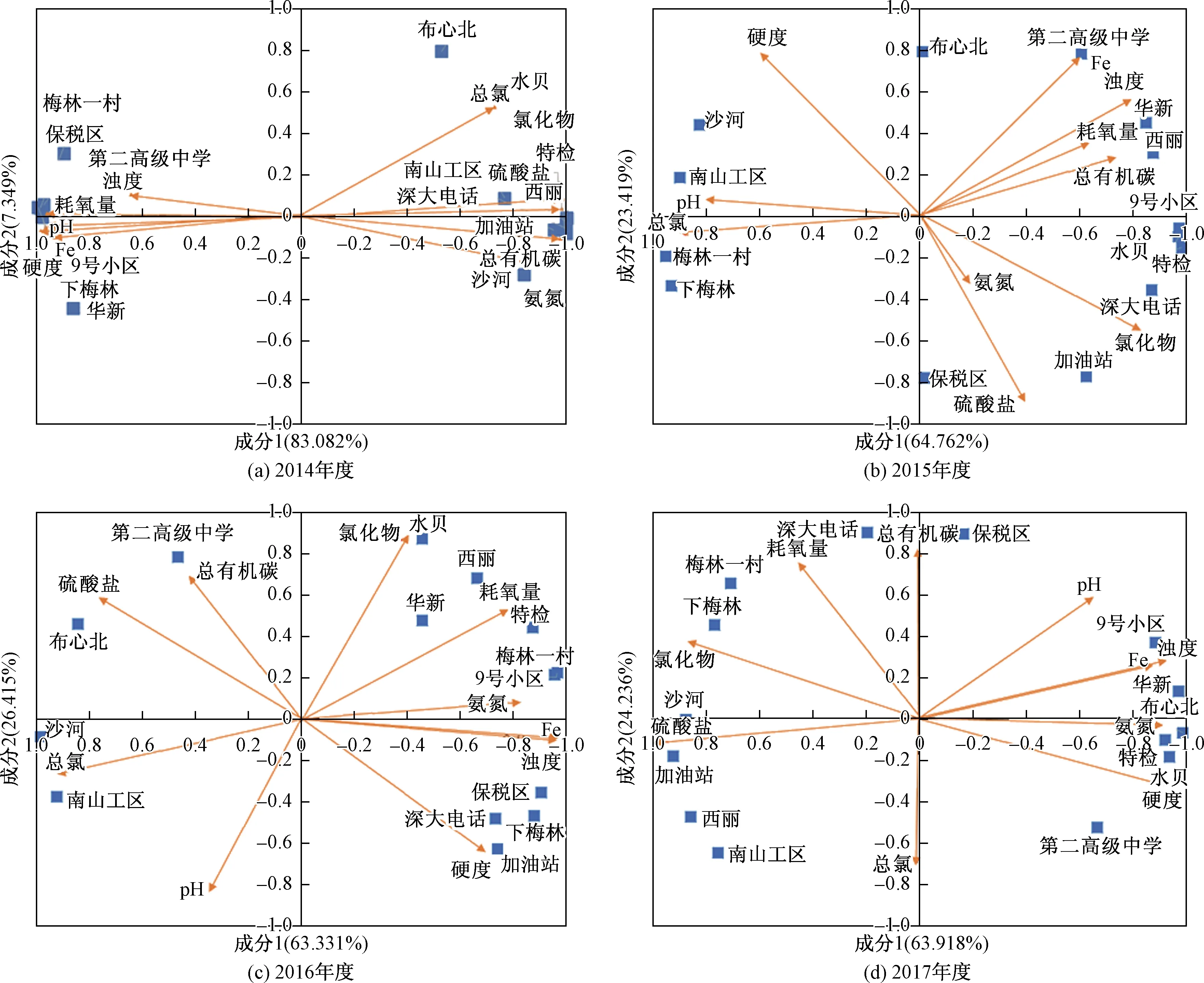
图5 分年度水质指标-采样点投影因子荷载图Fig.5 Projector load dingram betureen annual water quality indicator and Sampling sites

总体而言，各年度采样点及水质指标投影点在主因子轴上分布国年度不同而不同，但都呈远离中心分布，可将各年度全部投影点大致分为两类，一类由Fe、浊度、耗氧量指标，华新、9号小区采样点代表；一类由总氯和硫酸盐指标，沙河、南山工区采样点代表。由因子荷载投影图理论知，投影点位置越接近，相互之间关联性越强，因此，可以认为沙河和南山工区，华新和9号小区采样点间的水质更类似，Fe、浊度、耗氧量指标所反映水质信息的重叠度更高，以及Fe、浊度指标对华新、9号小区采样点的水质情况具有更强的解释性和反应力度。

从水质指标角度看，因子轴坐标代表投影点与不同主因子之间的相关性，综合四年情况，在单一信息贡献率超过60%的成分1轴上，Fe、浊度、硫酸盐、总氯、耗氧量的荷载绝对值大于其他因子荷载，结合向量垂线准则，水质指标垂点越接近采样点向量正向的水质指标对该采样点水质信息的解释比率越高，可以认为14个采样点的主要响应水质指标为Fe、浊度、硫酸盐、总氯、耗氧量。

从采样点角度看，成分 1 轴也反映了采样点的水质整体分异性，依据采样点主成分评价结果，综合4年情况对比分区，成分 1 轴荷载值高的采样点整体水质更优，荷载值低的采样点整体水质偏差。

3 结论

本文运用统计学方法对南方某市近4年供水管网末梢水水质的时空变化特征、主要响应指标及指标间相关性进行了研究分析。主成分分析法评价结果表明：1)该市管网末梢水年度总体水质存在差异，其中以2016年为最佳；2)夏秋季节更易出现水质异常现象，5～9月应加强管网末梢水水质管控；3)区域上看已完成深度处理改造的梅林水厂供水覆盖区管网末梢水水质最优，南山水厂供水覆盖区管网末梢水水质最差；4)水质指标硫酸盐、氯化物、硬度之间，Fe、浊度、总氯之间具有相对其他水质指标更高的相关性。对应分析法结果表明：1)该市管网水末梢水水质主要响应指标可重点关注Fe、浊度、总氯、硫酸盐和耗氧量；2)其中Fe、浊度、耗氧量呈正相关性强，上述指标与硫酸盐、总氯呈负相关性。