径向基函数在通榆河输水分析中的应用

潘道宏，谭成宇

(1.江苏省水文水资源勘测局 盐城分局，江苏 盐城 224015； 2.东台市水利建设总公司，江苏 东台 224220)

0 引 言

通榆河输水测验分析需要研究下游断面流量与其上游断面流量、河道沿线汇水、区域降雨、水工程运行调度等多种因素综合影响的复变函数关系。曼宁公式和圣维南方程组可用以解决此类问题，但也有很多情况不便使用。

神经网络简称人工神经网络，是一种数据处理模型，在生物神经网络启示下建立。它模拟相互连接的大量人工神经元进行计算，自动根据输入的信息调整网络结构和神经元间的权值，对输入数据进行建模。

本文尝试使用神经网络径向基函数模拟通榆河水面线、河道糙率分析计算、河道流量演算，效果较为理想。

1 径向基函数(RBF)网络基本原理

RBF网络能够逼近任意的非线性函数，具有良好的泛化能力，并有很快的学习收敛速度，已成功应用于非线性函数逼近、数据分类等。RBF网络是前向网络，它由3层构成：①输入层，节点个数等于输入维数；②隐含层，节点个数决定于问题复杂度，其节点与输入节点相连；③输出层，节点个数等于输出维数，其若干个线性单元与所有隐含节点相连。它的基函数采用径向基函数，把输入向量空间转换到隐含层空间，将线性不可分的问题转化位线性可分问题。

RBF网络分为正则化网络和广义网络，后者由前者稍加变化得到。假如有n个训练样本，从第i个隐含节点到第j个输出节点的权值为ωij,正则化径向基网络结构见图1。广义径向基网络结构见图2。

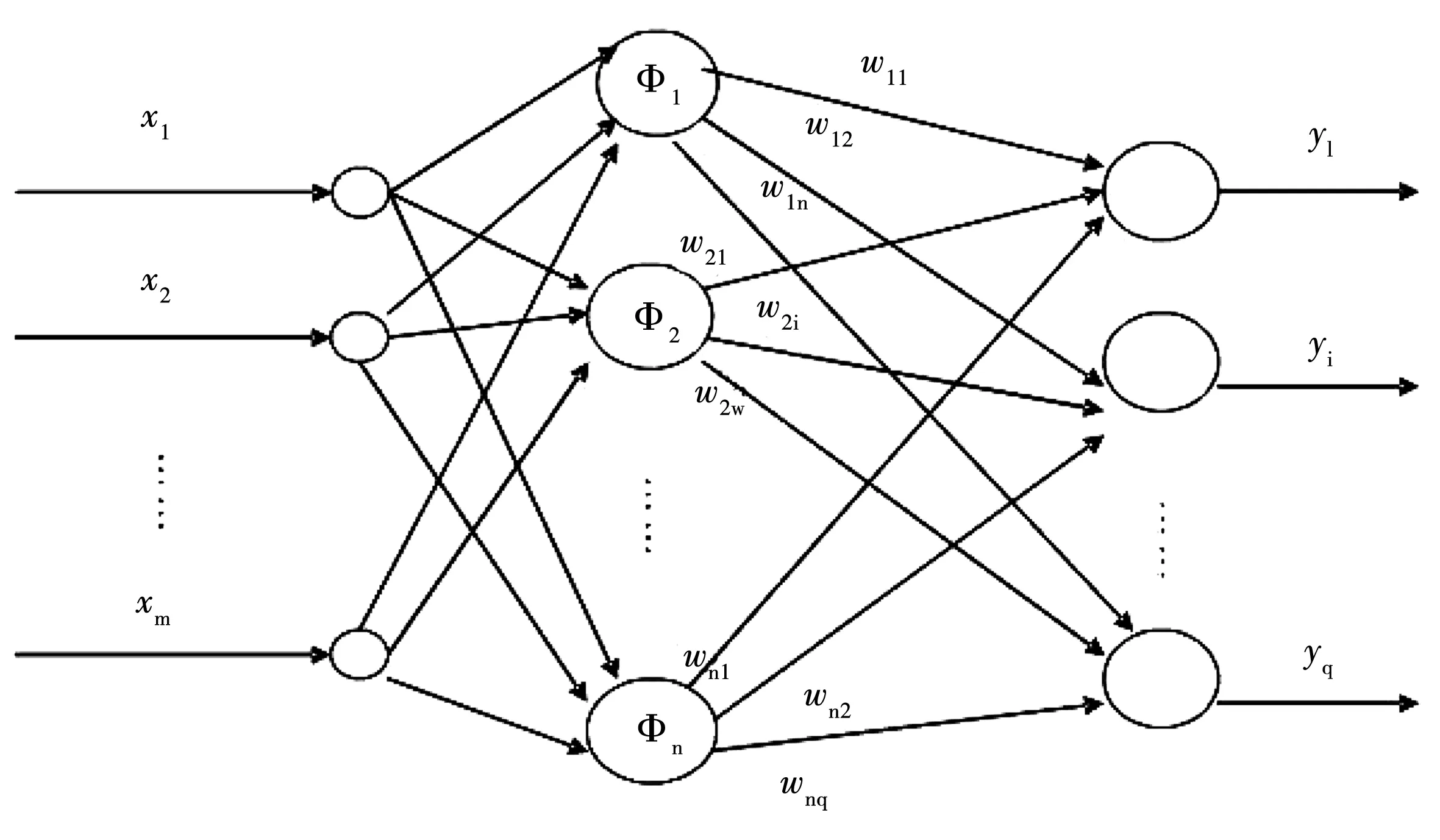
图1 正则化径向基网络结构

图2 广义径向基网络结构

与正则化网络类似，广义网络有m个输入节点。不同的是：

设实际输出Yk=[yk1,yk2…，ykj],输出单元的个数为j，则假设输入样本为Xk，第j个输出神经元的结果是：

选择了I个新的基函数φ(Xk,Xi)和相应新的权值ωij来逼近正则化网络中的N个隐含节点。

2 应用实例

2. 1 水面线模拟

以2006年(6月21日8时)通榆河东台(泰)-滨海枢纽(通)水面线(表1)进行分析。

表1 通榆河水面线(6月21日8时)

径向基网络目标误差设为0，扩散速度spread设为280。测试数据xx采用1～140的140个数据。程序如下：

plot(x,y,’ro’);

hold on;

xx=1:1:140;

yy=sim(net,xx);

plot(xx,yy,’c-’);

hold on;

y1=round(sim(net,x)*100)/100;

plot(x,y1,’b+’);

hold off;

legend(’输入原始数据’,’拟合线’,’拟合值’);

title(’径向基函数拟合得曲线’);

xlabel(’里程(km)’),ylabel(’水位(km)’),

拟合结果见图3。

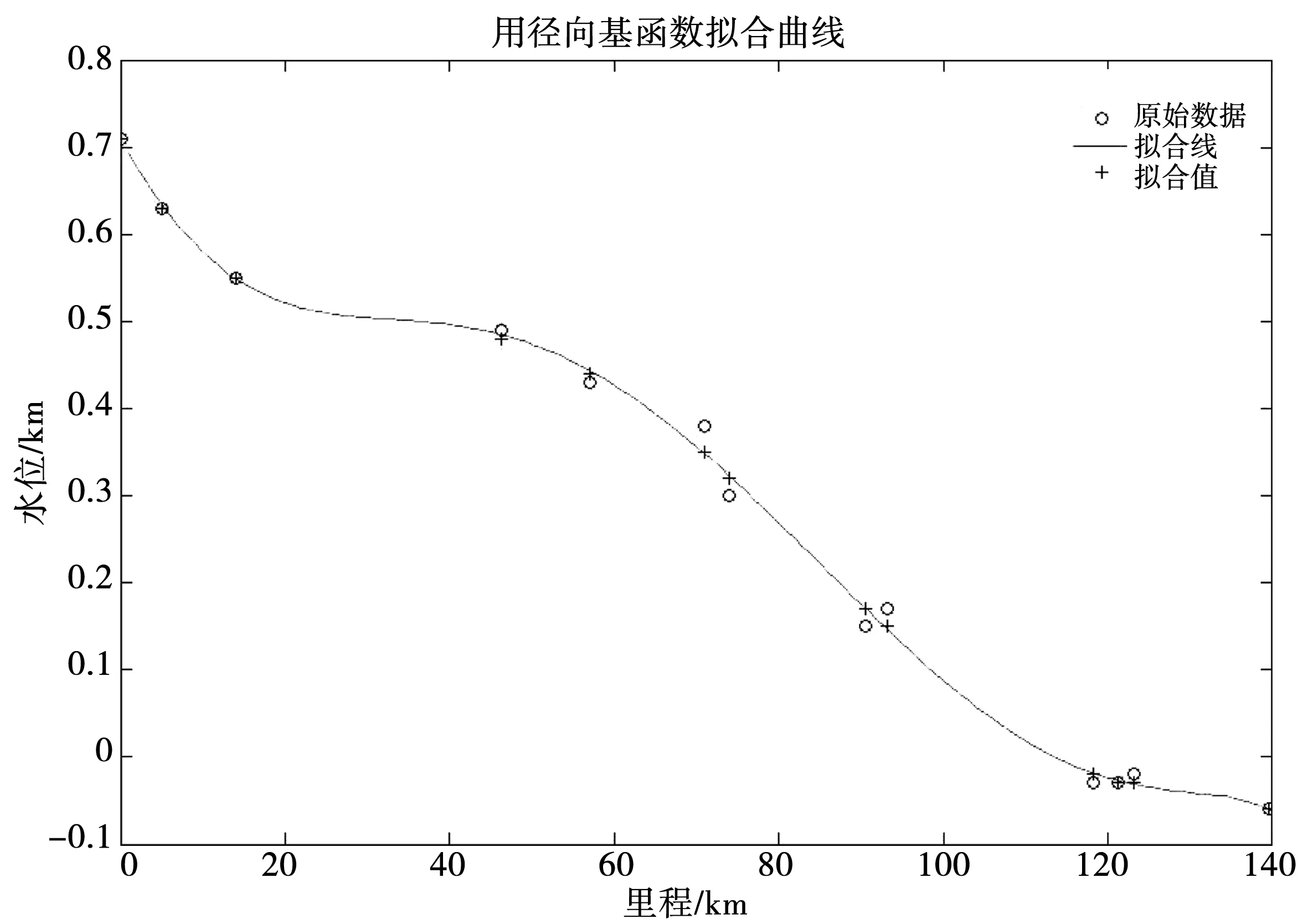
图3 通榆河水面线拟合结果(2006年6月21日8时)

由图3可见，径向基网络较好拟合了水面线，最大拟合误差0.03 m。误差情况见表2。

值得说明，如果spread选择过小，可能造成过学习。

表2 拟合误差情况表

2 .2 河道糙率计算和分析

2006-2010年供水期东台(通)-斗龙港段实测资料见表3。

表3 通榆河东台(通)-斗龙港段供水期河道糙率计算表

由曼宁公式知，断面流量与其上下游水位、过水断面面积、湿周、糙率等5个因素有关。应用网络，以断面流量、断面面积、湿周、东台(通)水位作为输入对糙率进行分类。

代码如下：

%%清空工作空间

clear,clc

close all;

rng(now)

M=4;

%% 定义输入样本

strr = {’东台(通)～斗龙港段20060616’,’东台(通)～斗龙港段20060623’,’东台(通)～斗龙港段20070609’,’东台(通)～斗龙港段20070617’,’东台(通)～斗龙港段20070622’,’东台(通)～斗龙港段20070606’,’东台(通)～斗龙港段20080616’,’东台(通)～斗龙港段20080627’,’东台(通)～斗龙港段20080605’,’东台(通)～斗龙港段20090618’,...

’东台(通)～斗龙港段20090629’,’东台(通)～斗龙港段20090625’,’东台(通)～斗龙港段20100603’,’东台(通)～斗龙港段20100613’};

data = [75.8,321,86.66,0.76; %20060616，即实测时间2006年06月16日，下同

93.6,324,86.86,0.87; %20060623

39.6,332,87.4,0.89; %20070609

80.3,302,85.29,0.60; %20070617

77.5,302,85.29,0.61; %20070622

60.2,345,88.45,1.09; %20080606

96.2,339,87.96,1.09; %20080616

128,37.4,90.55,1.48; %20080627

69.3,349,88.8,1.19; %20080605

53.4,337,87.87,1.02; %20090618

70.4,338,87.89,1.05; %20090629

79.4,312,85.93,0.75; %2009625

93,340,87.98,1.07; %20100603

80.9,340,87.98,1.06]’; %20100613

N=length(data);

%%建立网络

net = selforgmap([2,2]);

data = mapminmax(data);

tic

net = init(net);

net = train(net, data([1,2,3,4],:));

toc

%% 测试

y = net(data([1,2,3,4],:));

result = vec2ind(y);

score = zeros(1,M);

for i=1:M

t = data(:, result==i);

score(i) = mean(t(:));

end

[～,ind] = sort(score);

result_ = zeros(1,N);

for i=1:M

result_(result == ind(i)) = i;

end

fprintf(’ 测次 分类 ’);

for i = 1:N

fprintf(’ %-8s 第 %d 类 ’, strr{i}, result_(i)) ;

end

分类结果见图4。

图4 通榆河水面线(2006年6月21日8时)拟合结果

从图4分类结果看，径向基函数按照糙率的大小对数据进行分类，尽管输入项没有糙率，但数据间隐含的曼宁公式表达的规律已被挖掘出来。

2.3 河道流量演算

为说明神经网络的潜力，本文分别用马斯京根法和径向基函数演算通榆河流量问题。

2.3.1 马斯京根法

马斯京根法的公式为：

3个系数满足：

C0+C1+C2=1

现取2007年7月11日至8月2日东台(通)与大团(通南)站流量过程(表4)进行分析。

由表3数据率定马斯京根法流量演算模型参数K=9 665.6，X=4.2。大团(通南)流量率定最大相对误差11.5%，平均相对误差3.98%，最小相对误差0.0%。

运用率定参数K=9 665.6、X=4.2，由东台(通)2006年7月6-15日流量运用马斯京根法演算大团(通南)流量，见表5。

表4 马斯京根法流量演算模型参数率定表

表5 马斯京根法演算大团(通南)流量精度统计表

由表5可知，验证最大误差14.9%，平均相对误差7.06%，最小相对误差0.0%，精度较高。

2.3.2 神经网络法

由马斯京根法知:

大团(通南)流量t=F(东台(通)t-1,东台(通)t,大团(通南)t-1)

因此，选择NAR模型。网络结构见图5。

图5 NAR网络结构

确定训练数据、验证数据、测试数据分别为75%、15%、15%，神经元为10，延迟天数为1。结果表明，训练集17次、验证集3次输出值与目标值绝对误差在1.0～3.2。测试集3次中，第22次绝对误差为0；第6次绝对误差为-11.6，相对误差为-4.7%；第10次绝对误差为-28.4，相对误差为14.3%。精度优于马斯京根法。

3 结 语

本文从实例出发，用神经网络模拟河道水面曲线，对河道糙率数据进行深度挖掘，进而对河道流量演算问题进行研究。

模拟水面线的方法，还可应用于水位流量关系率定和仿真，对于编制防汛自动报讯系统具有重要潜在价值。分类方法可用于闸坝站水文出水流态判别、水文资料系列的一致性检查、模糊系统的聚类分析等可抽象成分类的问题。河道流量演算方面，神经网络相当于或高于马斯京根法精度，但操作更简便。如果把演算代码封装成仿真模块，可直接移植于防汛调度系统。