混凝土心墙坝蓄水前后应力位移规律浅析

刘诚炼 杨如东

（1、中国建筑一局有限公司华东分公司，浙江 杭州311200 2、西京学院，陕西 西安710123）

1 概述

“十二五”及“十三五”期间，我国土木水利工程中坝体建设呈现快速发展的态势，特别是新疆区，由于其特殊的地形地质条件和工程任务的要求，坝体的建设已经居于国际领先水平[1]。对于典型的混凝土心墙坝结构，在蓄水前后，坝体的应力和位移情况不尽相同，为探索相关规律，本文采用有限单元法通过对蓄水前后的混凝土心墙坝进行分析理，得出蓄水前后坝体的应力和位移变化情况。

有限单元法（FEM）是当今土木工程在工程分析中应用的较为最广泛应用的数值方法[2]。前人已经有有限单元法解决了大量的边坡稳定性问题，将使边坡稳定分析进入了一个新的时代[4～8]。有限元网格剖分的方法包括由几何实体生成网格法和网格直接生成法[9]。由于建立三维土石坝模型需要考虑材料分区、河谷形状、分层填筑等因素，则该模型几乎不可能自动化生成，需大量人工干预和手动剖分，且耗时几周甚至数月[9]。因此，本文将复杂的问题简化为平面应变问题，选择坝体及坝基的一处横截面进行计算。

2 有限元模型建立

2.1 模型数据及模型属性

坝高拟定为10m，坡度比为1:2，坝基宽度5m，长度60m。材料拟定为沥青混凝土，弹性模量为2×107，泊松比为0.3.密度为2415kg/m3，内摩擦角为30°，粘聚力为340kpa。

研究者多数在水坝边坡治理工程中采用的稳定安全系数是基于莫尔- 库仑准则的。因此本文采用Drucker-Prager 准则，即对于平面应变条件下的强度问题(比如边坡稳定安全系数、地基承载力等)，本文采用D-P 准则进行有限单元分析计算，由于D-P 准则分关联和非关联两种情况[10]。

采用非关联流动法则时(膨胀角ψ = 0 )：

采用关联流动法则时(膨胀角ψ=内摩擦角φ)：

但当材料为塑性剪切时，剪胀角控制着塑性体积应变的大小，并在塑性屈服阶段保持恒定。ψ=0 表示在剪切变形时体积保持不变。对于黏土，不包括超固结黏土，其剪胀角通常很小(ψ≈0)。对于砂土，其剪胀角和内摩擦角有关。对于内摩擦角φ＞30°的非黏性土(砂土、砾石土)，剪胀角约为ψ=φ-30°。剪胀角小于零的情况只适用于非常松散的砂土。对于大多数情况，都可以假设ψ=0。因此，本文仅采用非关联流动法则计算，计算得Drucker-Prager-α 系数为0.189，Drucker-Prager-k 系数为279.86×103。

2.2 几何建模

分别建立坝体及坝基在蓄水前后mises 应力，心墙的横向和竖向位移及最大最小主应力变化。蓄水前只施加重力，蓄水后在右边界施加边界荷载来模拟蓄水前后的受荷变化。

图1 坝体蓄水前mises 应力图

图2 坝体蓄水后mises 应力图

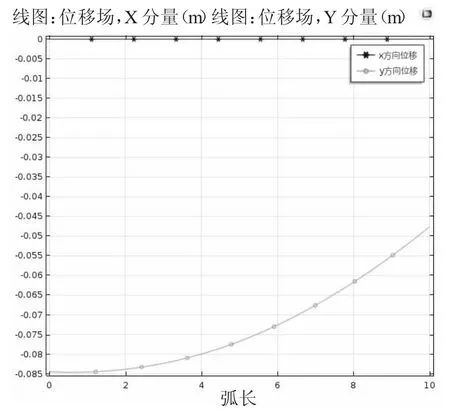
图3 坝体蓄水前位移下x，y 向位移图

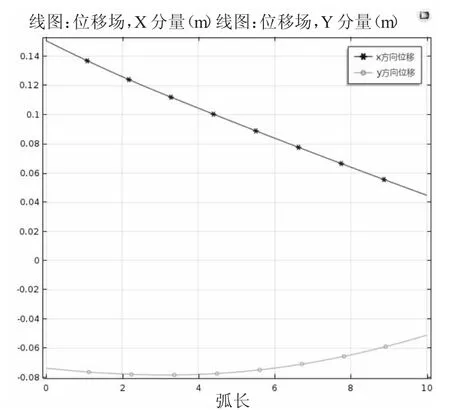
图4 坝体蓄水后位移下x，y 向位移图

图5 坝体蓄水前最大，最小应力图

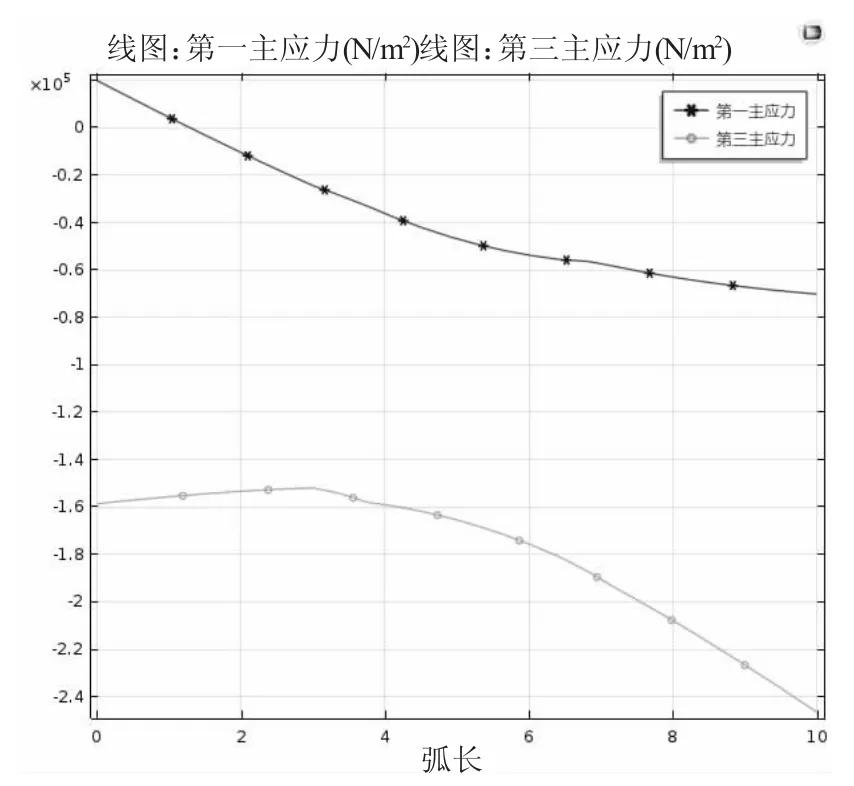
图6 坝体蓄水后最大，最小应力图

3 计算结果分析

3.1 坝体的应力变化

由于蓄水前只施加重力，因此应力集中出应出现在坝基底部中心处，与有限元计算结果相符。蓄水后在右边界施加边界荷载来模拟蓄水后坝体受水压力情况，因此应力集中出应出现在坝体与坝基右边界相接处，与有限元计算结果相符。具体应力分布见图1，图2。

3.2 心墙的位移及应力变化

蓄水前只施加重力，因此心墙在x 方向上不产生位移，y 方向最大位移约为0.085m。蓄水后心墙在x 方向上最大位移约为1.5×10-4m，y 方向最大位移约为0.085m，但分布规律发生变化。因此在蓄水前后，心墙在x 方向产生较大位移变化，在y 方向上最大位移不变，但分布改变，具体变化规律见图3，图4。并且可以得出，最大沉降量约为坝高的0.425%，出现位置约在坝高的2/5 处。

蓄水前心墙最大主应力为0.05Mpa，最小主应力为0.19Mpa。蓄水后心墙最大主应力为0.05Mpa，最小主应力为0.19Mpa。蓄水前心墙最大主应力为0.07Mpa，最小主应力为0.25Mpa，具体变化规律见图5，图6。按破坏准则计算，蓄水前最大应力水平为0.737，蓄水后最大应力水平为0.72，最大应力水平值小于1 表明心墙在蓄水前后均不会发生破坏。

4 结论

本文将较为复杂的三维有限元问题采用二维平面应变问题解决，从而缩小了建模的复杂程度和计算量。同时计算了基于D-P 准则的下的坝体有限单元法计算蓄水前后mises 应力，心墙的横向和竖向位移及最大最小主应力变化，推导出了在D-P准则下的Drucker-Prager-α 及Drucker-Prager-k 系数。对拟定尺寸的大坝进行二维有限元计算，结果表明：计算得出的大坝变形规律符合基本规律, 蓄水前后沥青混凝土坝心墙横向位移增大，最大竖向位移基本不变，且最大沉降量约为坝高的0.425%，出现位置约在坝高的2/5 处；心墙大小主应力按破坏准则计算最大应力水平值小于1，表明心墙在蓄水前后均不会发生破坏。