基于改进Gabor特征幻影的低分辨率人脸识别

卞加祁，胡学龙*，陈舒涵

(1.扬州大学 信息工程学院，江苏 扬州 225127；2.扬州大学 人工智能学院，江苏 扬州 225127)

0 引言

近年来，监控摄像头的应用颇为广泛，人脸识别系统备受重视。由于摄像头常处于非可控状态，故所拍摄得到的人脸图像一般分辨率较低且质量较差。如何提高此类低分辨率人脸的识别准确率具有重要的现实意义。目前，低分辨率人脸识别主要有超分辨率重建[1-6]和稳健特征提取[7-10]。超分辨率重建算法主要是先对低分辨率样本进行超分辨率增强，然后再进行识别。具体可以分为以下几类：基于流形学习、基于字典学习以及基于回归学习。在基于流形学习中，先假设高分辨率人脸和低分辨率人脸中具有相同的局部邻域结构，在这种假设下，可以通过邻域样本重建生成与低分辨率人脸相对应的高分辨率人脸；具体的流形思想有：局部几何结构以及稀疏邻域嵌入。在基于字典学习中，通过寻找和从低分辨率人脸和高分辨率人脸特征空间有关的稀疏编码系数来预测高分辨率人脸；基于字典学习的方法大致有2类：正交字典[3]和过完备字典。在基于回归学习中，首先通过高低分辨率人脸数据集，建立一个映射函数，再通过这个映射函数，来构建与低分辨率人脸相对应的高分辨率人脸。具体方法有核回归[5]、支持向量回归等。在超分辨率重建算法中，Pong等[11]提出了一种基于Gabor特征重建的低分辨率人脸识别，即先用局部线性回归建立一个映射函数，再通过这个映射函数，来构建高分辨率(HR)的Gabor特征；将预测得到的HR特征和低分辨率(LR)特征投影到GCCA[12]空间中，进行识别分类。

在该算法中存在一些不足：① 使用局部线性回归(LLR)[13]预测高分辨率人脸的Gabor特征，忽略了高低分辨率之间的非线性，本文采用流形学习中一种LLE[14]的算法预测高分辨率人脸Gabor特征，有效地预测了高分辨率人脸的非线性特征；② 通过Randomized CCA来揭示高低Gabor人脸特征的非线性关系，取代了原论文中使用GCCA仅能表示数据集之间线性关系的不足。

1 Gabor特征幻影

1.1 Gabor小波

Gabor小波与人类视觉系统中的简单细胞刺激响应非常相似。它在提取目标的局部空间和频率信息方面具有良好的特性。Gabor小波能够提供良好的方向和尺度选择特性，而且对于光照变化并不敏感，能够提供对光照变化良好的适应性，正是这些良好的特征，所以能够被广泛地应用于视觉。本文的人脸特征提取采用Gabor小波方法。在空间域中，由高斯函数调制的复指数构成，其公式为：

(1)

式中，(m，n)为人脸像素的位置；ω为复指数的径向中心频率；θ为Gabor小波的方向；σ为高斯函数的标准偏差。

1.2 高分辨率Gabor特征预测

Pong使用了局部线性回归的方法来预测高分辨率Gabor特征，这虽然能够在一定程度上预测高分辨率的Gabor特征，但只假设了高低分辨率之间存在线性关系。而在流形学习中，认为高低分辨率人脸具有相似的内在结构。相比于简单的局部线性回归，使用流形学习进行HR Gabor特征预测，更能准确地预测HR人脸。

嵌入算法在高分辨率人脸重建应用中，对于输入的低分辨率人脸特征：

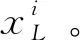
(2)

③ 通过结构权重和对应K个近邻的高分辨率来计算高分辨率Gabor人脸特征：

(3)

1.3 典型相关分析

(4)

1.4 随机CCA

虽然CCA能够最大化2组变量之间的相关性，但是CCA是基于线性相关的，所以不能准确反映非线性关系。为了克服CCA这一缺点，一系列的非线性拓展算法相继提出。比如Kernel CCA[15]，利用核函数来构造2组变量的非线性关系；再如Deep CCA[16]，利用DNN网络来训练2组变量的非线性关系；但是这些算法虽然提高了相关性，但也具有相当高的计算复杂度和时间复杂度。David[17]提出了利用随机策略来构造可以与线性算法结合使用揭示非线性特征。其公式为：

(5)

(6)

通过拉格朗日乘法，得出Urandom和Vrandom，即为：

(7)

为了避免过拟合，添加了μ和k两个惩罚项：

(8)

1.5 Gabor特征幻影的低分辨率人脸识别

类似于CCA，选择前d个特征值对应的特征向量Wl=(α1，α2，…，αd)和Wh=(β1，β2，…，βd)，将Wl，Wh称为广义典型投影向量，并且使用式(9)和式(10)组合的特征称为广义规范判别特征。即：

(9)

(10)

(11)

(12)

通过式(12)级联后并使用式(13)的计分函数将其分类：

(13)

式中，G和H表示训练集和测试集里的人脸投影到RCCA后的特征向量。

1.6 框架图

算法框架如图1所示，分为2个部分：训练部分和测试部分。训练部分：分别将高低分辨率的人脸数据集都基于Gabor进行特征提取，再通过RCCA获取LR和HR对应的相关特征，并将其线性连接；测试部分：输入一个LR的人脸，利用LLE构建HR的Gabor特征，分别将LR、HR映射到相关的特征中并进行线性连接；最后送入最近邻分类器进行分类，求得识别结果。

图1 算法框架

2 实验结果和分析

为了验证改进算法的有效性，在YALE和ORL数据集上做了一些实验，将LLE与LLR，GCCA与RCCA进行两两组合。保留PCA的97%的有效能量。实验环境为Intel Core i7 CPU 2.2 GHz，内存8 GB，操作系统Windows 10，编程平台为Matlab2017b。

2.1 数据集描述

YALE数据集由耶鲁大学计算视觉与控制中心创建，包含15名志愿者，每名志愿者由11幅图像组成，这些人脸包含着明显不同的光照、表情以及姿态的变化。以YALE数据集为基础，将48 pixel×48 pixel分辨率作为HR人脸图像集，对该数据集依次平滑下采样，依次获得8 pixel×8 pixel，9 pixel×9 pixel，11 pixel×11 pixel，13 pixel×13 pixel，15 pixel×15 pixel，17 pixel×17 pixel，19 pixel×19 pixel的LR人脸数据集。

ORL数据集由剑桥大学AT&T实验室创建，包含40名志愿者，每名志愿者由10幅图像组成，分辨率大小统一为92 pixel×112 pixel。该数据库人脸表情和人脸姿态有一定的变化。以ORL数据集为基础，将48 pixel×48 pixel作为高分辨率人脸图像集，对该数据集依次平滑下采样，依次获得10 pixel×10 pixel，12 pixel×12 pixel，14 pixel×14 pixel，16 pixel×16 pixel，18 pixel×18 pixel，20 pixel×20 pixel的低分辨率人脸数据集。

2.2 重建Gabor特征对比

在比对重建Gabor特征时，LR的Gabor特征分辨率为8 pixel×8 pixel，HR的Gabor特征的分辨率为48 pixel×48 pixel。如图2和图3所示。在YALE的人脸集中，采用峰值信噪比(PSNR)和结构相似度值(SSIM)对比LLR和LLE算法重建的Gabor特征，所考虑的尺度和方向分别为5和8。

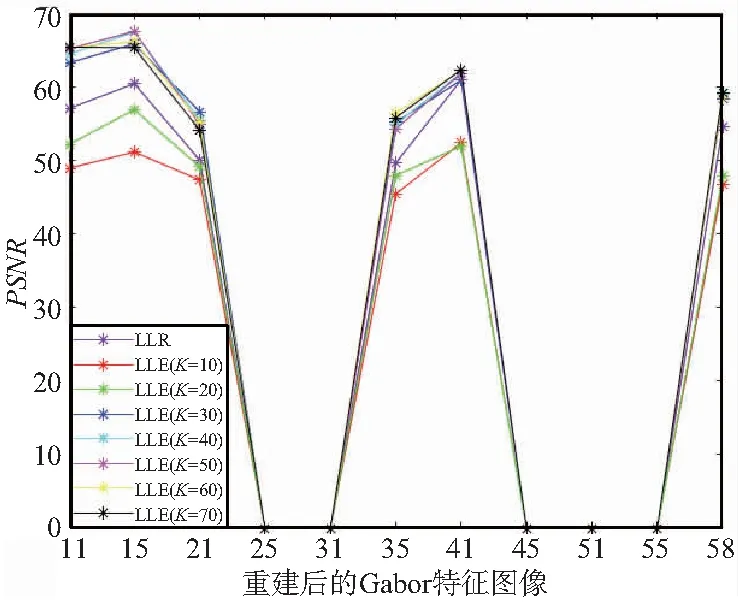
图2 重建Gabor特征得PSNR对比

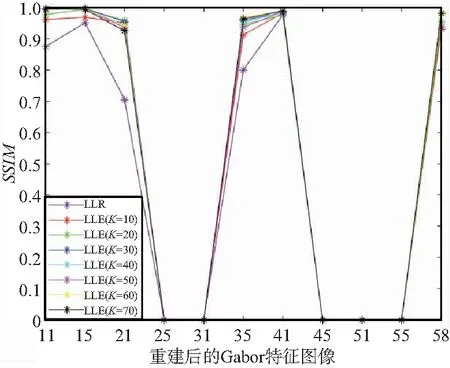
图3 重建Gabor特征得SSIM对比

从图2和图3可以得出，在PNSR的比对中，LLR算法重建特征效果好于K=10和K=20的，在K为30，40，...，70时，效果均小于LLE算法的重建效果；在SSIM的比对中，LLE算法的重建效果都好于LLR算法的重建。

2.3 YALE数据集上的实验

在YALE数据集的实验中，每位志愿者随机抽取5张人脸作为训练集，其余作为测试集。将48 pixel×48 pixel作为HR人脸，LR人脸范围9 pixel×9 pixel～19 pixel×19 pixel。在LLE算法中，K取值为30；RCCA中的惩罚项μ和κ设置为0.001。实验结果如表1和图4所示。

表1 YALE上不同算法在不同分辨率下的识别率

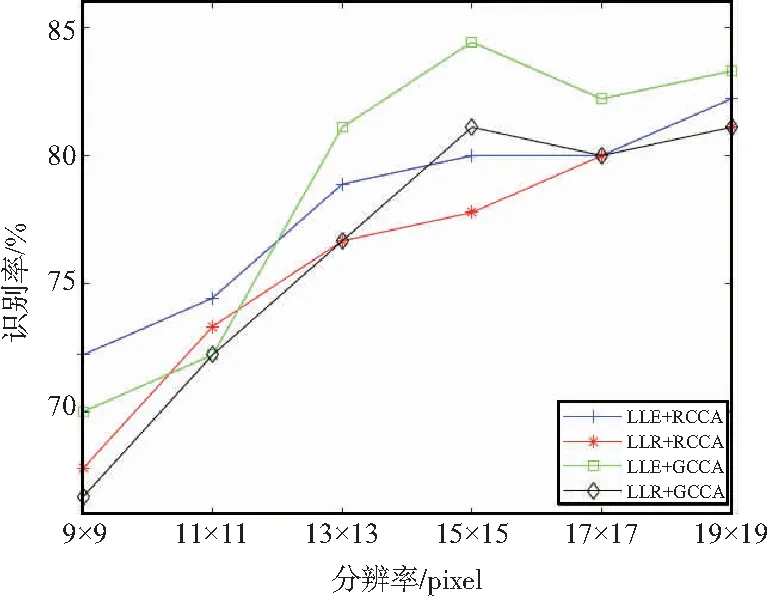
图4 YALE上各类算法识别率

通过实验结果比对，本文基于LLE算法而改进的重建HR人脸的Gabor特征，在不同分辨率下，识别率均高于原论文中基于LLR算法而重建的HR人脸Gabor特征；本文所提出的基于LLE重建Gabor特征，结合原论文中的GCCA算法，能够在不同的LR下拥有最高的识别率；本文提出的LLE+RCCA的改进算法在不同分辨率下普遍高于原算法的LLR+GCCA的组合，尤其是在超低分辨率9 pixel×9 pixel时，依然有72.22%的识别率。

2.4 在ORL数据集上的实验

在ORL人脸数据集的实验中，每位志愿者随机抽取5幅人脸作为训练集，其余作为测试集，以48 pixel×48 pixel作为HR人脸，LR范围10 pixel×10 pixel～20 pixel×20 pixel。在LLE算法中，K值选取为40；RCCA中的惩罚项μ和κ设置为0.001。实验结果如表2和图5所示。

表2 ORL上不同算法在不同分辨率下的识别率

图5 ORL上各类算法识别率

更换实验数据集，将实验放在ORL数据集上测试。由于ORL数据集的环境干扰比较少，所以识别率普遍提高。也得到和YALE数据集相似的结论：本文基于LLE算法而改进的重建HR人脸的Gabor特征，在不同分辨率下，识别率均高于原论文中基于LLR算法而重建的HR人脸Gabor特征；本文所提出的基于LLE重建Gabor特征，结合原论文中的GCCA算法，能够在不同LR下拥有最高的识别率；本文提出的LLE+RCCA的改进算法在不同分辨率下普遍高于原算法的LLR+GCCA的组合，尤其是在超低分辨率10 pixel×10 pixel时，依然有86.50%的识别率；

3 结束语

本文提出了基于改进的Gabor特征幻影的人脸识别算法，在Pong的算法上提出了改进。主要有以下2点：采用基于流形学习的LLE算法取代原论文的LLR算法，更加注重高低分辨率之间的非线性关系；在特征投影方面，采用RCCA算法，更加注重训练集的非线性特征。在上述实验结果中，改进后的算法提高了识别率，尤其是极低分辨率的情况下。