基于人工神经网络的地基长期沉降变形预测
唐 凯 湖南省第五工程有限公司
1 引言
建筑物及构筑物在服役期中,其地基常产生显著的长期沉降,而由于地基长期沉降变形的存在,易导致建筑物或构筑物在服役期间产生许多安全问题。因此,如何精准的预测地基的长期沉降变形并针对该问题进行及时处理就变得十分重要。目前,国内外已经有许多学者针对地基长期沉降变形问题展开了十分深入的研究[1-6]。魏星等[7]已针对长期交通荷载作用下的软土地基沉降变形进行有限元分析,并在此基础上得到可合理表征软土地基长期沉降变形的经验公式;黄文华等[8]采用数值试验和室内试验结合的方式针对某工业建筑地基长期沉降变形进行深入研究,结果表明地基最大沉降位置为建筑物中心位置,其研究结果为工业建筑的长期服役性能优化提供了科学指导。除上述方法外,考虑到地基长期沉降变形的影响因素较多,其各因素之间的相关性不明确,韩汝才[9]和夏江[10]等尝试采用人工智能算法对地基沉降进行预测,并取得了较好的成果,在此基础上,张慧梅等[11]利用神经网络算法构建模型对软土地基沉降进行预测,并认为网络模型可较好地反应地基沉降变形特征,且可反应多个因素对地基沉降变形的影响。
综上所述,目前虽已经有诸多学者针对地基沉降预测进行了深入研究,但考虑到实际工程情况较为复杂,且仍缺乏精准的地基长期沉降预测方法,仍需针对软土地基长期沉降预测开展深入研究。因此,本研究拟结合人工神经网络算法,构建可实现地基长期沉降预测智能化模型,并结合实际工程案例进行深入分析。
2 人工神经网络模型的建立
2.1 人工神经网络工作原理
人工神经网络算法基于生物神经网络结构提出,其具有智能化特征。一般而言,神经网络算法以多个因素作为输入变量,当输入变量输入进神经网络后,输入变量将通过多个网络节点最终达到输出层,在整个网络模型运算过程中,各个网络节点将按某种设定方式对输入数据进行数学化处理,实现最终输出结果与实际结果的误差最小化。区别于一般的数学模型,神经网络模型将直接建立输入变量与输出变量之间高度的非线性关系,并进一步对构建的对应关系实现预测。
2.2 网络模型结构设计
一般而言,神经网络模型包含三个类型的层次结构,分别为输入层、隐含层以及输出层。针对不同类型的工程实际情况,其每一个模型层所包含信息均不一致,本研究结合某工业区具体情况,构建得到含单个隐含层的网络模型,其最终网络拓扑结构如图1所示。需要说明的是,在进行研究过程中,输入层变量分别设定为时间(t/天),填土厚度(H/cm),处理层填土厚度(H-c/cm)以及土体综合模量(M/MPa),输出层变量则为地基监测沉降量(S)。

图1 网络模型拓扑结构
根据以上所建立的网络模型,其中隐含层节点数目需要进一步计算得到,其具体计算方式见公式(1)。

在进行模型训练及预测过程中,需要采用归一化方法对输入变量数据Ii进行预处理。在本研究中,所采用的归一化方法如公式(2)所示。
将预处理后变量Ii输入网络,与此同时,将采用所设置完毕的初始权重(Wi)j、偏置以及传递函数对下层输出值(h)j进行计算,其计算流程如公式(3)所示。

式中:
[(fx)]——传递函数。
在本研究中该函数采用tansig函数,如具体表达式如公式(4)所示。

当计算得到隐含层输出值后,利用初始化后的隐含层与输出层之间的连接权值(wjk)及偏置进一步计算得到输出层输出值(Ok),如公式(5)所示。
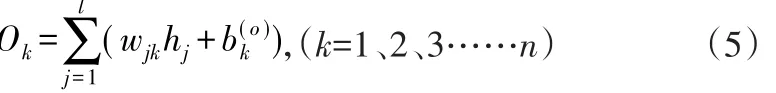
当输入变量向前传播至输出层并计算得到输出值后,进一步利用全局均方差误差对模型训练精度进行判断,全局均方差误差可由公式(6)计算得到。

式中:
S— —训练样本组数;
——第p组样本输出变量实测值。
当误差无法符合预期,模型则利用梯度下降算法进行反向传播以重新调整各个层间权值(w)、金额偏置(b),其调整方式如公式(7)和(8)所示。

式中α为学习效率。
3.1 工程实例概况及模型训练

图2 模型训练误差
本研究以株洲某工业区为例,所选取变量分别为时间(t/天),填土厚度(H/cm),处理层填土厚度(H-c/cm)以及土体综合模量(M/MPa),其中处理层填土厚度以及土体综合模量均为固定值,对于本工程而言,其处理层填土厚度为9.0cm,土体综合模量为45.7MPa。针对该工程地基沉降进行长期监测后获取327天沉降变形数据,在进行神经网络模型计算时,选取前60天数据进行模型训练,得到模型训练误差如图2所示。从图中可以看出,该模型训练后误差较小,可较好地反应该工程地基沉降情况。
3.2 预测结果分析
3 工程实例验证
进一步采用训练后模型对该工程地基长期沉降变形进行预测,得到最终结果如表1所示。从表中可知,整体而言,预测结果和检测结果差距较小,在工程后94天以及327天时,其监测沉降变形分别为199.0mm和215.0mm,其预测结果分别191.0mm和210.0mm,绝对误差均小于10%,可初步认为该网络模型可较完备地反应地基长期沉降变形特征,且具有较高精度。

表1 预测结果
为更精准地分析该网络模型的预测能力,进一步对比预测结果和实测结果得到如图3所示的结果,从图3中可知,整体而言,该模型输出结果和实测结果匹配程度较好,表明该模型具有较为优越的预测能力,不仅可较好地反应短时期内的地基沉降变形特征,且能较好地表征地基长期变形特征,通过短期内实测数据进行模型训练即可实现地基变形的长期预测,模型简便,所需物理参数较少,具有重要的实际工程意义,可有效地指导实际工程。

图3 预测结果与实测结果对比
4 结论
本研究针对实际工程施工过程中的地基长期沉降变形问题,将人工神经网络算法引入进预测模型中,构建可实现地基长期沉降预测的神经网络模型,并结合株洲某工业区实际案例,对其工程价值进行分析,得到主要结论如下。
a)结合实际工程情况以及地基沉降监测数据实现模型训练,表明该模型可达到较高的预测精度,且可充分反应各个因素对地基沉降变形特征的影响,能有效地反应地基沉降变形特征。
b)将训练完成模型用于地基长期沉降变形预测,结果表明该模型预测精度较好,其预测值和实测值误差较好,该模型科学合理,原理简便,具有重要工程意义。

