基于排队博弈的最优比特币交易费支付策略

黄冬艳，李 浪

（广西无线宽带通信与信号处理重点实验室（桂林电子科技大学），广西桂林 541004）

0 引言

比特币［1］是以区块链技术为支撑的一种数字货币。在比特币系统中，数据以区块（block）为单位产生和存储，并按照时间顺序连成链式（chain）数据结构。区块之间通过哈希值进行关联。后一个区块的哈希值由前一个区块的哈希值、随机数以及若干等待处理的交易关参数共同决定。新区块的创建需得到全网多数节点的确认并向各节点广播实现全网同步。任何一个区块的改动将会导致该区块的哈希值发生变化，从而与链上其他区块的哈希值无法匹配。因此，比特币具有去中心化、难以篡改等特性，受到广泛关注。其底层技术区块链的应用已经延伸到智能制造［2］、物联网［3-5］、供应链［6］、电力竞价［7］交易等领域。

比特币网络的共识机制为工作量证明（Proof of Work，PoW）。在PoW 共识机制下，为获得记账权或称出块权，每个参与节点必须找到符合条件的哈希值所需要的随机数。寻找随机数的过程称为“挖矿”，参与“挖矿”的节点称为矿工。

目前矿工的收益由挖矿奖励和交易费两部分组成［8］。挖矿奖励是指，伴随着新区块的产生会生成一定数量的比特币，作为挖出该区块的矿工的工作奖励；交易费也称手续费，由用户自行设置，交易费作为额外奖励发给处理该交易的矿工。

交易费的存在增加了欺诈交易与无效交易的成本，从一定程度上避免了系统滥用；同时，交易费的高低很大程度上影响着交易的优先级。由于比特币中每一个区块的空间大小有一定限制，矿工需要依据多种因素（如块龄、交易费、交易大小等），选择将待处理的交易打包进入区块。为最大化自身的收益，矿工往往更愿意处理交易费高的交易。因此，交易费越高的交易被优先打包进入区块的概率越高，相应的交易耗时就越少。实际上，自2016 年初以来，比特币网络容量的限制已经造成交易之间的竞争，从而导致更高的费用，免费交易彻底成为过去式。零费用或非常低费用的交易鲜少被处理，有时甚至不会在网络上传播［8］。文献［9］的调查结果也表明，交易的处理速度与交易的金额无关，而与交易费强相关，非零交易费的交易的处理速度比零交易费的交易要快。

对用户而言，交易能否被快速处理和所需交易费都是其关心的主要问题。交易费过高增加了用户交易成本，过低则会增加用户的交易耗时。因此，研究交易费与交易耗时之间的关系有助于揭示系统的交易运作规律，从而帮助用户选择合适的支付策略。

文献［10］研究了在股权证明的联盟链中，共识延迟与用户交易费之间的权衡。文献［11］结合排队理论，分析了区块链中的三个关键性能指标（系统中的平均交易数、单个区块中的平均交易数、交易的平均确认时间），设计了一个具有两个不同服务阶段的马尔可夫批量服务排队系统。文献［12］通过在用户交易之间引进第三方保险机构的做法来解决比特币的双花风险问题，给用户提供了交易安全保障。文献［13］将比特币交易按照交易金额大小分类，发现小额交易（交易金额小于1比特币）的用户占比更高，处理速度更慢。文献［14-16］基于排队论研究了系统容量、交易速率等问题。以上文献分析了系统容量、交易安全和交易速率等，但未能考虑用户之间的博弈以及用户个体的策略性决策行为对交易速率的影响。

结合排队博弈论，本文研究了比特币网络中用户交易手续费对交易耗时的影响，旨在为用户提供最优的交易手续费支付策略。本文的主要贡献如下：1）将比特币网络中交易排队竞争上链的过程建模为一个带优先权的非抢占型排队博弈模型；2）分析了交易费对交易耗时的影响并推导出用户的纳什均衡支付策略。

1 系统模型

一笔交易从提交到比特币系统中到被记录到区块中的过程如图1 所示。由PoW 共识机制决定，比特币的交易不是实时完成的，只有交易被写入区块并广播交易才算完成。通常认为，连续篡改6 个以上区块［8］难度极大，因此真正确认一笔交易需经历6个区块。

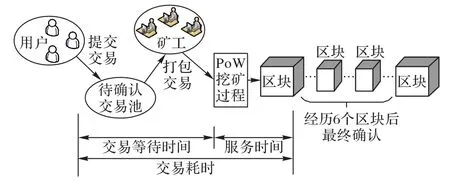
图1 交易上链示意图Fig.1 A transaction going up on blockchain

每个区块的大小上限为1 MB［17］（比特币在2017年8月24日实施了隔离见证（Segregated Witness，SegWit）方案，将交易数据与交易签名进行了分离，区块的实际大小仍为1 MB，但是加上签名信息后，总大小突破了1 MB 上限）。其中，前50 KB 保留给UTXO（Unspent Transaction Output）优先级高的交易，剩下的区块空间由其他交易竞争，矿工优先选择交易手续费高的交易来填充剩下的空间。

交易的UTXO 优先级由交易的UTXO 模型［8］决定。UTXO从被记录到区块链中到当前交易处理时的区块链末端所经历的区块数，称为“块龄”。交易输入值高、“块龄”大的交易比那些新的、输入值小的交易拥有更高的优先级。具体地，UTXO优先级的定义为：

其中：N是交易的总输入个数，l表示交易的总大小，Vi表示交易第i个部分输入的金额，单位是聪，Ai是其“块龄”。当一笔交易的Hp＞5.76×107时（相当于1 比特币、块龄为144（大约为1 d）、交易大小为250 B），可以被打包进前50 KB中。

由于相较于1 MB 的区块空间，前50 KB 的字节占比很小，后面的大部分的区块空间通过交易费的高低竞争。因此本文仅讨论交易手续费对交易耗时的影响。交易耗时为交易的等待时间与交易的处理时间之和，如图1 所示。其中，等待时间为交易提交到系统到被打包进区块的时间，交易处理的时间为服务时间，也即挖矿过程。

后续分析中的优先级区别于UTXO 优先级，专指用户通过支付交易费获得的被优先打包进入除前50 KB 字节以外的区块空间的优先权。

2 排队博弈模型与均衡支付策略

2.1 排队模型

假设每个到达的用户不知道当前系统中的交易数量，也不知道其他用户支付的交易费。用户在进队时要选择最优的支付策略使得自己的总花费最小，并且交易一旦提交交易费不可更改。

矿工处理交易的流程如图2 所示。矿工根据交易费将当前交易池中的交易按照交易费高低进行排序，选取当中的前若干笔交易组成一个批次进行处理，生成一个区块，该批次中的交易费虽有不同，却一同被处理，因此将其视为同优先级的一笔业务，用其交易费均值表示此笔业务的优先级。接着，矿工开始进行PoW 工作处理这笔业务。基于PoW 的特性，交易一旦选定不可更改，因此，此时到达系统的交易无论交易费的高低，都必须等待当前交易处理完毕，即非抢占型优先权。基于比特币的出块特性（一次只能出一个单块），因此将矿工视为单一性服务台处理。一笔业务交易处理完成后，加入新到达的交易，对交易池进行重排列。

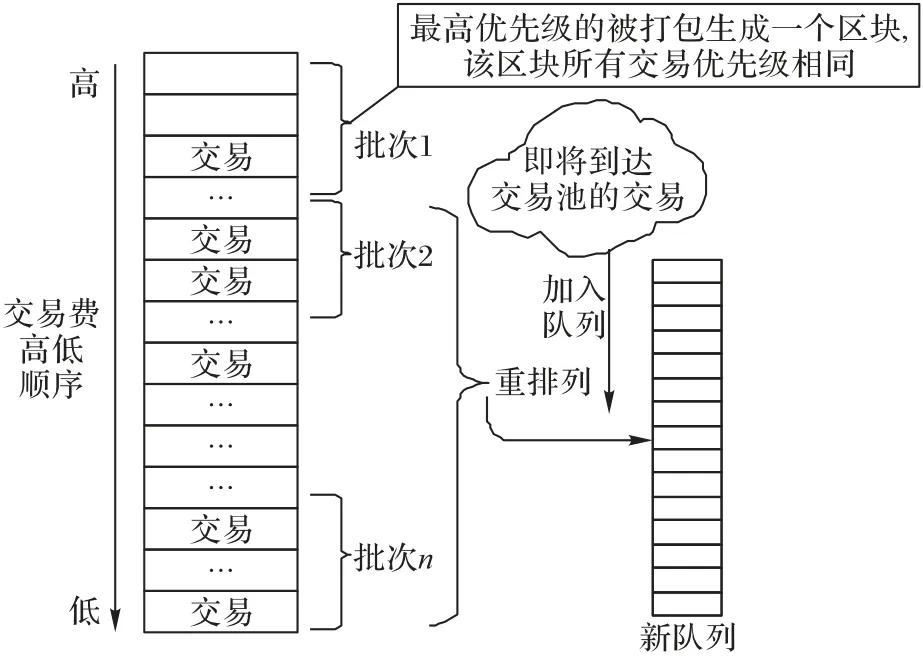
图2 矿工交易处理流程Fig.2 Miners processing transactions

参照文献［17-18］，本模型设定交易到达（指批次，下同）是参数为λ的泊松流，交易的处理时间（服务时间）服从参数为μ的指数分布。记ρ=，为系统的拥塞指标。ρ越大意味着系统越拥挤，在区块生成时间稳定的情况下意味着交易量增大。因此，整个过程可建模为一个有非抢占型优先权和随机服务的M/M/1排队系统。

2.2 平均交易耗时

假设当前系统中有n批交易，且n≥0。第i批用户ui支付的交易费均值为xi，则用户ui的优先级等价于交易费的总占比出，即

2.3 均衡交易费支付策略

命题2 设单位等待费用为c，用户总花费为x+cW(x)，用户的纳什均衡支付策略为支付交易费-x，有：

证明 假设所有批次交易支付的交易费为1，若最优策略为支付，需满足：

由式（9）可知，W(x)是下凸函数，因此当c＞0时必存在唯一最优解-x。求解式（14）可以得到式（13）。证毕。

3 仿真与评估

3.1 交易费对交易耗时的影响

根据式（9）得到平均交易耗时随交易费的变化如图3所示。

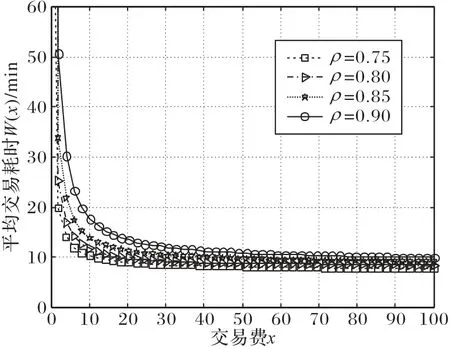
图3 不同ρ下平均交易耗时随交易费的变化Fig.3 Average transaction time changing with transaction fee with different ρ

从图3 中可以看出，给定系统拥塞ρ，用户的平均交易耗时随着交易费的增加而减小。在支付交易费一定时，如果交易增多，系统的拥塞指标增大即系统交易量增大，则用户的平均交易耗时也会随之增加。

3.2 用户的交易费支付策略

不同交易费支付策略下用户的平均交易耗时与用户的总花费的对比分别如图4和图5所示。

图4 平均交易耗时对比Fig.4 Comparison of average transaction time

从图4 中可以看出，在不同的系统状态下，用户采用均衡支付策略都可以将平均交易耗时维持在服务时间附近，即用户可以获得最高优先级，享受优先服务。当ρ=0.5 时，均衡支付策略的耗时约为7.7 min，比x=ρ策略减少了38%，比不支付交易费策略减少了61.3%。当ρ=0.9（系统高负荷）时，均衡支付策略的平均交易耗时比不支付交易费策略减少了98%，比x=ρ支付策略减少了81.2%。

同时从图5 可以看出，虽然采用均衡策略需要支付交易费，但是因为交易耗时下降，时间成本大幅度降低，所以用户的总花费相对更小。当ρ=0.7 时，均衡支付策略的用户总花费比支付x=ρ的策略下降了45%，比不支付交易费的策略下降了79.5%。当ρ=0.9 时，均衡支付策略的用户总花费比支付x=ρ的策略下降了72%，比不支付交易费的策略下降了97%。从图4和图5可以看出，随着ρ的增大，均衡支付策略的优势更加明显。

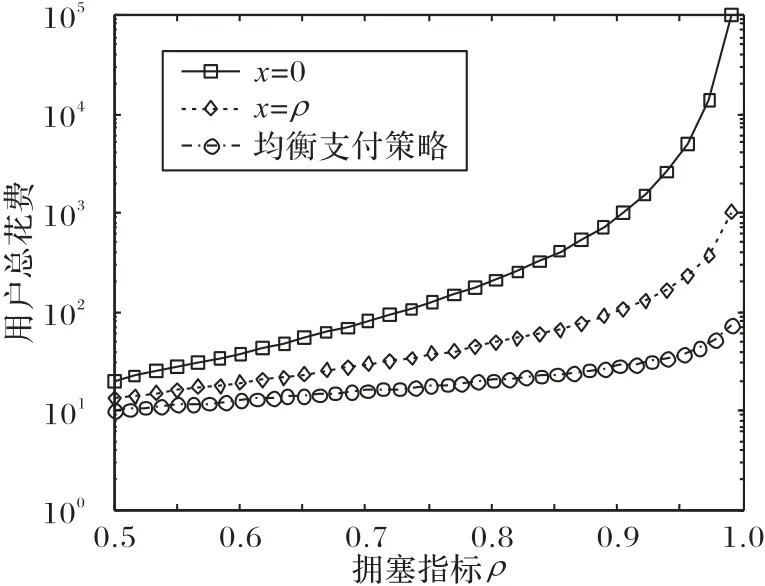
图5 用户总花费对比Fig.5 Comparison of user total cost

综上所述，用户可根据系统拥塞程度采用最优的支付策略，保证交易被尽快处理的同时避免过高的交易费支出；另一方面，用户还可以根据系统拥塞程度和自身对交易耗时的要求，根据命题1 的结论，计算出保证自己的交易在预期时间内上链所需的交易费。

4 结语

本文通过排队博弈论研究了比特币系统中交易费对平均交易耗时的影响，推导出了平均交易耗时与交易费、系统拥塞指标之间的关系式，并给出了用户的纳什均衡支付策略。在后续研究中，可以从矿工收益出发，考虑区块大小一定的情况下，如何选择交易填满有限的区块空间来最大化矿工收益的问题。